強くなるロボティック?プレイヤーの作り方 5章
1 like413 views
強くなるロボティック?プレイヤーの作り方 5章 間違えているところや疑問点などがありましたら下記のツイッターアカウントまでご一報ください。 @gen_goose_gen
![マウンテンカー問題
○モデル化
状態 位置：
速度：
行動 推力：
（右への力）
（推力なし）
（左への力）
連続空間
離散空間
諸条件
台車の質量：m=0.2[kg]
摩擦係数：k=0.3[-]
ステップ幅：⊿t=0.1[s]
報酬関数
この式は変だとは思います…](https://image.slidesharecdn.com/roboticchapter5up-170515044021/85/5-7-320.jpg)
![マウンテンカー問題
○モデル化
状態 位置：
速度：
行動 推力：
（右への力）
（推力なし）
（左への力）
連続空間
離散空間
諸条件
台車の質量：m=0.2[kg]
摩擦係数：k=0.3[-]
ステップ幅：⊿t=0.1[s]
報酬関数](https://image.slidesharecdn.com/roboticchapter5up-170515044021/85/5-37-320.jpg)
![マウンテンカー問題
○モデル化
状態 位置：
速度：
行動 推力：
（右への力）
（推力なし）
（左への力）
連続空間
離散空間
諸条件
台車の質量：m=0.2[kg]
摩擦係数：k=0.3[-]
ステップ幅：⊿t=0.1[s]
報酬関数](https://image.slidesharecdn.com/roboticchapter5up-170515044021/85/5-46-320.jpg)
![アクロボット
○状態空間と行動空間の設計
：左回転のトルク
：トルクなし
：右回転のトルク
関節の角度[rad] 関節の角速度[rad/s]
状態空間（連続）：
行動空間（離散）：
○報酬関数の設計
：アクロボットの上半身が垂直に
近いほど報酬が大きくなる](https://image.slidesharecdn.com/roboticchapter5up-170515044021/85/5-50-320.jpg)
強くなるロボティック?プレイヤーの作り方 5章
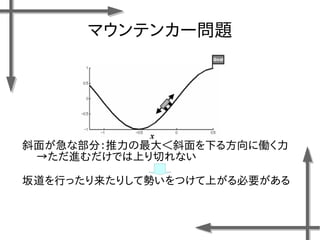
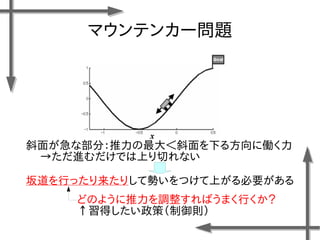
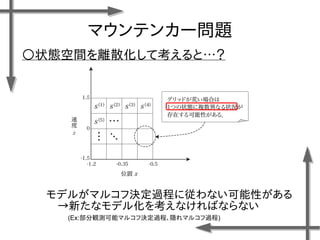
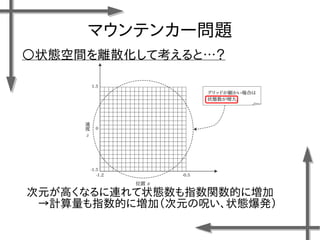
- 8. マウンテンカー問題 ○状態空間を離散化して考えると…？ (Ex:部分観測可能マルコフ決定過程、隠れマルコフ過程) モデルがマルコフ決定過程に従わない可能性がある →新たなモデル化を考えなければならない
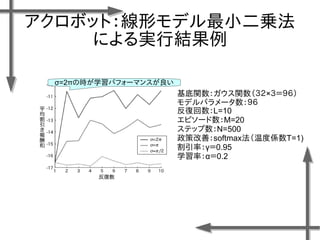
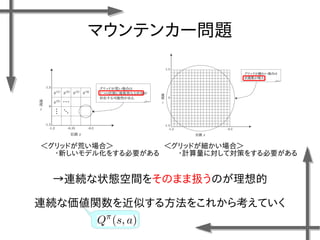
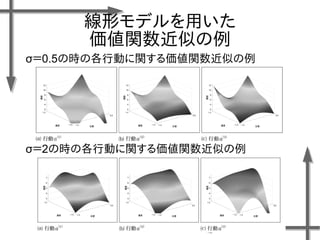
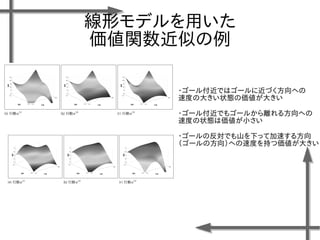
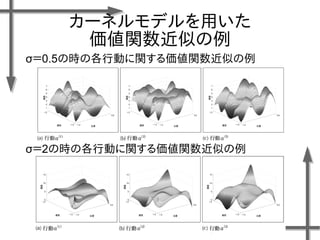
- 38. 線形モデルを用いた 価値関数近似の例 基底関数 ((36個のガウス関数） 政策 二次元状態空間上のグリッドの中心点 {-1.2, -0.35, 0.5}×{-1.5, -0.5, 0.5, 1.5} 位置 速度 関数I(x)の定義 エピソード数M＝20、ステップ数T=20の標本データ、割引率γ＝0.95
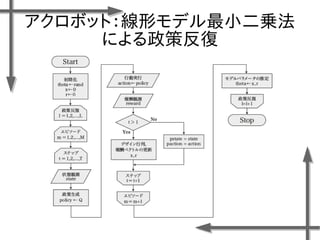
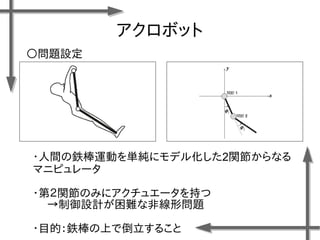
- 49. アクロボット ?人間の鉄棒運動を単純にモデル化した2関節からなる マニピュレータ ?第２関節のみにアクチュエータを持つ →制御設計が困難な非線形問題 ?目的：鉄棒の上で倒立すること ○問題設定
- 54. ありがとうございました！！