![Altın cetvel oluşturmak için;
Şekildeki gibi öncelikle bir doğru parçasını ( beyaz )
altın oran oluşturacak şekilde iki parçaya [AB]'e
( mavi ) ve [AC]' ye ( sarı ) bölüyoruz. Ve aynı mantıkla
hareket ederek [AB] doğrusunu da iki altın parçaya
bölüyoruz ve bunu devam ettirerek 2. şekildeki
doğruları elde ediyoruz.](https://image.slidesharecdn.com/altnoran-150315063623-conversion-gate01/85/Altin-oran-11-320.jpg)
Altın oran
- 2. ALTIN ORANA GİRİŞ TARİHTE ALTIN ORAN İNSANLARDA ALTIN ORAN HAYVANLARDA ALTIN ORAN İհİDE ALTIN ORAN ALTIN ORAN VE SANAT ALTIN SÖZLÜK
- 3. Dünyanın, insanların, bitkilerin, ağaçların... , kısacası Kainat'ın yaratılışında yaratıcının kullandığı orandır.Aynı zamanda insanlar da teknolojide ve hayatta bu oranı kullanmaktadırlar. Kısaca biz altın orana "göz nizamının oranı" diyebiliriz. Çoğu zaman doğayı gözlediğimizde bu oranın varlığını görebiliriz.
- 5. ALTIN ORANIN TARİHÇESİ ► Altın orana ilişkin matematik bilgisi ilk kez İ.Ö. 3. Yüzyılda Öklid’in Stoikheia ("Öğeler") adlı yapıtında "aşıt ve ortalama oran" adıyla kayda geçirilmiştir. Eldeki veriler,bu bilginin geçmişinin aslında Eski Mısır’da İ.Ö. 3000 yılına kadar dayandığını göstermektedir. Grek dünyasına da Pythagoras ve Pythagoras’cular tarafından tanıtıldığı ileri sürülür. ► Altın oran, (Fi) sayısı olarak bilinir. Bu sayı, Eski Yunan düşünürleri tarafından bulunmuştur, ancak Fi sayısını kimin tanımladığı kesin olarak belli değildir. Eski Yunan düşünürlerinin bazılarının, Fi sayısının yerine (to) sayısını kullandıkları da bilinmektedir. ► İ.Ö. 500’lü yıllarda yaşamış olan tüm zamanların en büyük matematikçilerinden biri olan Pisagor (Pythagoras), altın oranla ilgili aşağıdaki düşüncelerini dile getirmiştir: ► Bir insanın tüm vücudu ile göbeğine kadar olan yüksekliğinin oranı, bir pentagramın uzun ve kısa kenarlarının oranı, bir dikdörtgenin uzun ve kısa kenarlarının oranı, hepsi aynıdır. Bunun sebebi nedir? Çünkü tüm parçanın büyük parçaya oranı, büyük parçanın küçük parçaya oranına eşittir. ► Altın oran, günlük yaşantımızda, matematiğin estetik güzelliğe etki ettiği her alanda karşımıza çıkan bir kavramdır. Altın oranın çok çeşitli tanımları verilebilir ama altın oran, neticede matematiksel bir kavramdır ve değeri de 1,618033.... olarak devam eden ondalık bir sayıdır. Altın oranın matematiksel anlamına geçmeden önce altın oranın karşımıza çıktığı bazı alanlara değinelim. ► Altın oran, örneğin bir dikdörtgenin göze en estetik gözükmesi için uzun kenarı ile kısa kenarı arasındaki orandır. Buna benzer olarak, bir doğru parçasının ikiye ayrıldığında göze en hoş gelen ikiye ayrılma oranıdır. Altın oran, sadece dikdörtgen ve doğru için değil, neredeyse tüm geometrik cisimler ve yapılar için kullanılabilir.
- 6. FİBONACCİ KİMDİR? Orta çağın en büyük matematikçilerinden biri olarak kabul edilen Fibonacci İtalya'nın ünlü Pisa şehrinde doğmuştur. Çocukluğu babasının çalıştığı Cezayir'de geçmiştir. İlk matematik eğitimini Müslüman bilim adamlarından almış ve İslam aleminin kitaplarını incelemiş ve çalışmıştır. Avrupa'da Roma rakamları kullanılırken ve sıfır kavramı ortalarda yokken Leonarda Arap rakamlarını ve sıfırı öğrenmiştir.
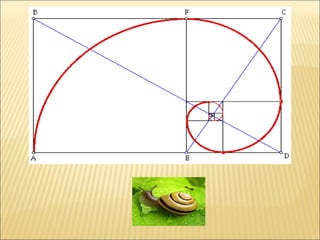
- 7. Tabiatta çok fazla karşılaşılan Fibonacci sayı dizisi bu mantıkla elde edilmektedir. Dizi şöyledir: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55… Dizinin ilerleyen sayılarında alınan bir terimin bir önceki terime oranı altın orana yakınlaşmaktadır. Bu dizi deniz kabuğu spirallerinin oranlarını ve ayçiçeğindeki çekirdeklerin dizilişini belirler.
- 10. Altın oran ve insanı incelemeden evvel resimlerdeki renklerle insanda altın oranın nasıl oluştuğunu anlayabilmek için, renklerin anlamını görelim. Öncelikle bir altın cetvel oluşturalım, ve buna göre resimlerdeki altın oranı inceleyelim.
- 11. Altın cetvel oluşturmak için; Şekildeki gibi öncelikle bir doğru parçasını ( beyaz ) altın oran oluşturacak şekilde iki parçaya [AB]'e ( mavi ) ve [AC]' ye ( sarı ) bölüyoruz. Ve aynı mantıkla hareket ederek [AB] doğrusunu da iki altın parçaya bölüyoruz ve bunu devam ettirerek 2. şekildeki doğruları elde ediyoruz.
- 12. Kısaca ; Mavi çizgi: Beyaz çizginin altın bölümü Sarı çizgi: Mavi çizginin altın bölümü Yeşil çizgi: Sarı çizginin altın bölümü Pembe çizgi: Sarı çizginin altın bölümüdür.
- 13. İnsan parmaklarında görülen altın oran; Şekilde işaret parmağınızın her bölümü bir öncekinden 1,618...( yani altın oranın değeri ) kadar büyüktür ve üstteki cetvele dikkat ederseniz her bölüm 2, 3, 5, 8 e yani ardışık fibonacci sayılarına karşılık gelmektedir. Şekilde pembe, yeşil, sarı ve mavi çizgiler altın oranı gösterir.
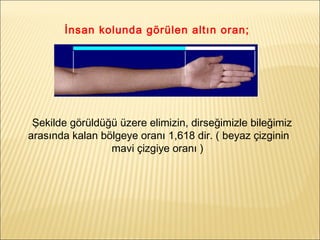
- 14. İnsan kolunda görülen altın oran; Şekilde görüldüğü üzere elimizin, dirseğimizle bileğimiz arasında kalan bölgeye oranı 1,618 dir. ( beyaz çizginin mavi çizgiye oranı )
- 15. İnsan yüzünde görülen altın oran; Şekildeki resimde de gördüğünüz gibi kafa bir altın dikdörtgenin içinde. Kulaklar arasındaki mesafe, gözle üst dudak arasındaki, burnun altı ile çene arasındaki mesafe (resimde mavi çizgi ile gösterilmiş) hep altın oran içermektedir. Resmi incelerseniz daha başka altın oranlar da görebilirsiniz. Bunlarda sarı ve yeşil çizgilerle gösterilmiştir.
- 16. DNA'da Altın Oran Canlıların tüm fiziksel özelliklerinin depolandığı molekül de altın orana dayandırılmış bir formda yaratılmıştır. yaşam için program olan DNA molekülü altın orana dayanmıştır. DNA düşey doğrultuda iç içe açılmış iki sarmaldan oluşur. Bu sarmallarda her birinin bütün yuvarlağı içindeki uzunluk 34 angström genişliği 21 angström'dür. (1 angström; santimetrenin yüz milyonda biridir) 21 ve 34 art arda gelen iki Fibonacci sayısıdır.
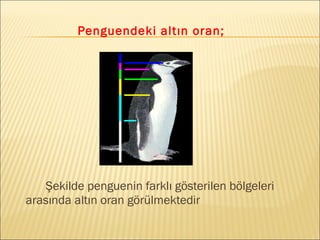
- 18. Penguendeki altın oran; Şekilde penguenin farklı gösterilen bölgeleri arasında altın oran görülmektedir
- 19. Kelebekteki altın oran; Şekildeki kelebeğin hem eninde hem boyunda gösterilen delikler arasında altın oran görülmektedir.
- 20. YUNUSTAKİ ALTIN ORAN; Şekilde yunusta boyunda burnu ve kuyruğu arasındaki bölgede, kuyruk bölgesinde enine ve de süzgeç kısmında altın oran görülür.
- 21. Deniz kabuğundaki altın oran; Şekildeki deniz kabuğunda farklı renklerle gösterilmiş bölgelerdeki altın oranı fark edebildiniz mi?
- 23. Şaşırtıcıdır ki karıncalardada bu orana rastlanır resimde görünen organaller arasındaki oranlar altın orandır. pembenin yeşile sarının yeşile ... oranları altın orandır.
- 25. ALTIN ORAN VE İհİ
- 26. EĞER BİR BİTKİYİ DİKKATLE İNCELERSENİZ FARK EDERSİNİZ Kİ, YAPRAKLAR ,HİÇ BİR YAPRAK ALTTAKİ YAPRAĞI KAPAMAYACAK ŞEKİLDE DİZİLMİŞTİR. BU DA DEMEKTİR Kİ, HER BİR YAPRAK GÜNEŞ IŞIĞIN EŞİT BİR ŞEKİLDE PAYLAŞIYOR VE YAĞMUR DAMLALARI BİTKİNİN HER BİR YAPRAĞINA DEĞEBİLİYOR. BİR BİTKİNİN SAPINDAKİ YAPRAKLARIN, BİR AĞACIN DALLARININ ÜZERİNDE HEMEN HER ZAMAN FİBONACCİ SAYILARI BULURSUNUZ. EĞER YAPRAKLARDAN BİRİ BAŞLANGIÇ NOKTASI OLARAK ALINIRSA VE BUNDAN BAŞLAYARAK, AŞAĞIYA YA DA YUKARIYA DOĞRU, BAŞLANGIÇ NOKTASININ TAM ÜSTÜNDE VEYA ALTINDA BİR YAPRAK BULUNCAYA KADAR YAPRAKLAR SAYILIRSA BULUNAN YAPRAK SAYISI FARKLI İհİ İÇİN DEĞİŞİK OLACAKTIR AMA HER ZAMAN BİR FİBONACCİ SAYISIDIR.
- 27. MESELA, YANDAKİ RESİMDE EN BAŞTAKİ DALI İNCELERSEK, BAŞLANGIÇ NOKTASI OLARAK 1 NUMARALI YAPRAĞI ALIRSAK, KENDİSİYLE AYNI YÖNDE BİR BAŞKA YAPRAKLA KARŞILAŞABİLMEMİZ İÇİN 3 DEFA SAAT YÖNÜNDE BİR DÖNÜŞ YAPMAMIZ GEREKİR VE BU ESNADA 5 TANE YAPRAK SAYARIZ. EĞER BU DÖNÜŞÜ SAAT YÖNÜNÜN TERSİNDE YAPARSAK 2 TANE DÖNÜŞ GEREKECEKTİR. VE 2, 3, 5 ARDIŞIK FİBONACCİ SAYILARDIR. YANDAKİ RESİMDE YER ALAN DALI İNCELEDİĞİMİZDE İSE 8 YAPRAK ÜSTÜNDEN GEÇTİĞİMİZ 5 TANE SAAT YÖNÜNDE DÖNÜŞ YAPARIZ. SAAT YÖNÜNÜN TERS İSTİKAMETİNDE İSE BU DÖNÜŞ SAYISI 3 OLACAKTIR. 3, 5, 8 İSE ARDIŞIK FİBONACCİ SAYILARIDIR. ARDIŞIK FİBONACCİ SAYILARININ BİRBİRİNE ORANI ALTIN ORANA YAKLAŞTIĞINDAN BAHSETMİŞTİK. DEMEK OLUYOR Kİ BİTKİNİN YAPRAKLARININ ÇIKIŞINDA BİLE ALTIN ORAN GÖRÜLÜR. BUNU ÜSTEKİ BİTKİ İÇİN ŞÖYLE DEYAZABİLİRSİNİZ. 3/5 (SAAT YÖNÜNDEKİ DÖNÜŞ BAŞINA YAPRAK SAYISI)
- 28. AYÇİÇEĞİ VE ALTIN ORAN ALTIN ORANI ayrıca çiçeklerin tohumlarında da görülebilir. Eğer bir papatyanın ve ya bir ayçiçeğinin çiçek kısmını büyütseniz muhtemelen yandaki resme benzer bir görüntü elde edersiniz. Eğer şekildeki modelde, saat yönünde olan ve saat yönünde olmayan sarmalları sayarsanız, 21 ve 34 sayılarını elde edersiniz ki bu sayıların oranı altın oran olan sayısına eşittir.
- 29. Altın Oranı sadece ayçiçeklerinde veya papatyalarda değil, bir kıvırcığın yapraklarında bir ananas veya kozalakların kat kat kabuklarında, soğanın katmanları arasında da rastlayabilirsiniz. İşte aşağıda kozalaklar ALTIN ORANI çok açık bir şekilde gösterirler. Kırmızı ve yeşil spiralleri sayın ve oranlayın altın oran kırmızı=13 yeşil =8
- 30. ALTIN ORAN VE SANAT Türk mimarisi ve sanatı da altın orana ev sahipliği yapmıştır. Mimar Sinan'ın da bir çok eserinde bu altın oran görülmektedir. Mesela Süleymaniye ve Selimiye Camileri'nin minarelerinde bu oran görülmektedir Türk mimarisi ve sanatı da altın orana ev sahipliği yapmıştır: Konya'da Selçukluların inşa ettiği İnce Minareli medresenin taç kapısı, İstanbul'daki Davut Paşa Camisi, Sivas'ta Mengüçoğulları'dan günümüze miras kalan Divriği Külliyesi genel planlarından kimi ayrıntılarına dek f ile iç içe bir görünüm sunar.
- 31. Eski Yunanda da altın dikdörtgen bir çok sanat dalında kullanılmıştır. Bunlardan bir tanesi de Atina'daki Partenon 'dur. Partenon İ.Ö. 430 ve ya 440 yıllarında Athena adlı tanrıça için yapılmıştır. Tapınağın orijinal planları elimizde olmasa da , tapınağın uzunluğu genişliğinin kök 5 katı olan bir dikdörtgen üzerine inşa edildiği gözükmektedir. Ayrıca aşağıdaki resimlerde görebileceğiniz gibi tapınakta daha başka altın dikdörtgenlerde göze çarpmaktadır. (altın dikdörtgen kenarları oranı altın oran olan dikdörtgenlerdir.)
- 32. Altın oran sadece Yunanlılar tarafından kullanılmamıştır. Mısır'daki Keops piramidinde, Paris'in ünlü Notre Dame Katedralinde altın oranın izlerini görmek mümkündür.
- 33. Eski Mısırlılar inşa ettikleri piramitlerde de altın oranı olduğu saptanmıştır. Piramitlerin tabanı ile yüksekliği arasındaki oranın 0.618 ( yani altın oranın değeri )olduğu görülmüştür. Ayrıca piramitlerin dizilimi yani bulundaki bölgeye yerleşimi de bize altın spirali verir. Bu da şekilde aşağıdaki şekilde açıkça gösterilmiştir. Sonuç olarak piramitler hem kendi içerisinde hem de birbirleri arasında altın oran içermektedir
- 34. Mona Lisa'nın başının etrafına bir dikdörtgen çizdiğinizde ortaya çıkan dört kenar bir altın dikdörtgendir. Bu dikdörtgeni, göz hizasında çizeceğiniz bir çizgiyle ikiye ayırdığınızda yine bir altın oran elde edersiniz. Resmin boyutları da altın oran oluşturmaktadır.
- 35. Bu tamamlanmamış resimde, aziz altın dikdörtgenin içine sığmaktadır. Bunun bir tesadüf olmadığı, Leonardo da Vinci'nin matematiğe olan ilgisini resme taşıdığına inanılmaktadır.
- 36. Burada Leonardo da Vinci'nin insan vücudunda altın oranı gösteren tablosudur
- 37. BURADA ; ► Altın Dikdörtgen ► Altın Üçgen ► Altın Spiral ÖRNEKLERİ GÖSTERİLECEKTİR
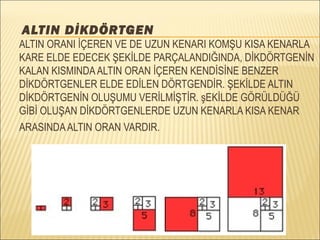
- 38. ALTIN DİKDÖRTGEN ALTIN ORANI İÇEREN VE DE UZUN KENARI KOMŞU KISA KENARLA KARE ELDE EDECEK ŞEKİLDE PARÇALANDIĞINDA, DİKDÖRTGENİN KALAN KISMINDAALTIN ORAN İÇEREN KENDİSİNE BENZER DİKDÖRTGENLER ELDE EDİLEN DÖRTGENDİR. ŞEKİLDE ALTIN DİKDÖRTGENİN OLUŞUMU VERİLMİŞTİR. şEKİLDE GÖRÜLDÜĞÜ GİBİ OLUŞAN DİKDÖRTGENLERDE UZUN KENARLA KISA KENAR ARASINDAALTIN ORAN VARDIR.
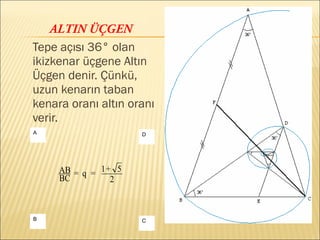
- 39. ALTIN ÜÇGEN Tepe açısı 36° olan ikizkenar üçgene Altın Üçgen denir. Çünkü, uzun kenarın taban kenara oranı altın oranı verir. DA CB 2 5+1=q= BC AB
- 40. ► Altın spiral: Altın dikdörtgenin içinde şekildeki gibi çizilen spirale altın spiral denir.
- 41. ALTIN ORAN KULLANILAN DİĞERALTIN ORAN KULLANILAN DİĞER YERLERYERLER Kar Kristallerinde Altın Oran Uzayda Altın Oran Evrende, yapısında altın oran barındıran birçok spiral galaksi bulunur.
- 42. ► Bir grup insana birçok üçgen ve dikdörtgen içerisinden bir üçgen ve bir dikdörtgen seçmeleri istendiğinde büyük çoğunluğunun altın üçgeni ve altın dikdörtgeni seçtikleri görülmüştür. ► Ayrıca otomotiv devi TOYOTA otomobil tasarımında altın oranı kullanmıştır.