Breadth First Search with example and solutions
Download as PPTX, PDF0 likes50 views
BFS
1 of 23
Download to read offline









Recommended
bfs tree searching ,sortingUntitled presentation.pptx



bfs tree searching ,sortingUntitled presentation.pptxsaurabhpandey679381
╠²
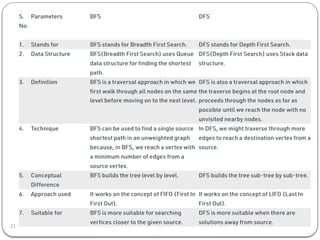
Breadth First Search (BFS) is a graph traversal algorithm that explores all vertices in a graph level-by-level starting from a specified starting vertex. It uses a queue data structure to keep track of vertices to be explored. The time complexity of BFS is O(V+E) where V is the number of vertices and E is the number of edges, as it visits all vertices and edges in the worst case. The space complexity is O(V) as all vertices may need to be stored in the queue.Lecture 12 Heuristic Searches



Lecture 12 Heuristic SearchesHema Kashyap
╠²
The document describes heuristic search algorithms including best first search, branch and bound search. Best first search maintains a priority queue of nodes and expands the node with the lowest cost function first. Branch and bound finds the optimal solution by keeping track of the best solution found so far and abandoning partial solutions that cannot improve on the best. It uses pruning to reduce the number of explored nodes. Both algorithms use concepts like traversing the root node and its neighbors in ascending order of distance from the root until reaching the goal node.PPT ON INTRODUCTION TO AI- UNIT-1-PART-2.pptx



PPT ON INTRODUCTION TO AI- UNIT-1-PART-2.pptxRaviKiranVarma4
╠²
The document discusses different types of agents and problem solving by searching. It describes four types of agent programs: simple reflex agents, model-based reflex agents, goal-based agents, and utility-based agents. It also covers formulating problems, searching strategies, problem solving by searching, measuring performance of searches, types of search strategies including uninformed and informed searches, and specific search algorithms like breadth-first search, uniform cost search, depth-first search, and depth-limited search.Lec 15-graph Searching in data structure and lgorithm.pptx



Lec 15-graph Searching in data structure and lgorithm.pptxhinamazhar6
╠²
Lec 15-graph Searching in data structure and lgorithm.pptxBfs and dfs



Bfs and dfsutsav patel
╠²
The document discusses Breadth First Search (BFS) and Depth First Search (DFS) graph traversal algorithms. BFS uses a queue data structure and explores neighbor nodes level-wise, starting from a source node. Its time and space complexity is O(V+E) and O(V) respectively. DFS uses a stack and explores nodes by going deeper first until reaching a dead end, then backtracks. Its complexity is O(V+E) for adjacency lists and O(V^2) for adjacency matrices. Both algorithms are used for path finding, cycle detection and other graph applications.Uninformed search /Blind search in AI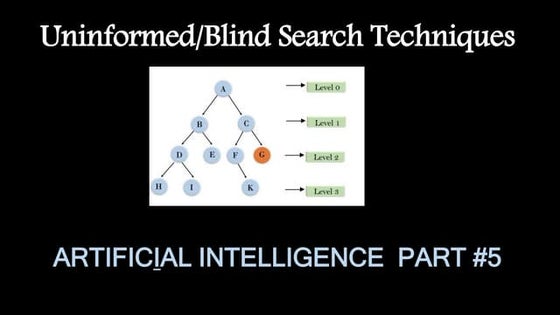



Uninformed search /Blind search in AIKirti Verma
╠²
here is my 5th ppt on state space search and problem solving techniques.
must my watch my videos on my youtube channel techiseasy
Final slide4 (bsc csit) chapter 4



Final slide4 (bsc csit) chapter 4Subash Chandra Pakhrin
╠²
The document describes various search algorithms used to solve pathfinding problems represented as graphs. It discusses uninformed searches like breadth-first search (BFS) and depth-first search (DFS) as well as methods for evaluating search performance in terms of completeness, time complexity, space complexity, and optimality. BFS uses a queue to expand shallow nodes first, guaranteeing an optimal solution but with exponential time and space costs. DFS uses a stack to expand deep nodes first, providing better space efficiency but not guaranteeing an optimal solution.RPT_AI_03_PartB_UNINFORMED_FINAL.pptx



RPT_AI_03_PartB_UNINFORMED_FINAL.pptxRahulkumarTivarekar1
╠²
Iterative deepening search is an uninformed search strategy that combines the benefits of depth-first and breadth-first search. It gradually increases the depth limit in iterations, starting from 0, until a goal is found. This occurs when the depth limit reaches the depth of the shallowest goal node. Iterative deepening search is optimal, complete, and has reasonable time and space complexities. It is suitable for problems with large search spaces where the solution depth is unknown.Lecture 16 - Dijkstra's Algorithm.pdf



Lecture 16 - Dijkstra's Algorithm.pdfiftakhar8
╠²
For the family tree data structure, I would recommend using a graph represented by an adjacency list. This allows easy traversal of the connections between ancestors and descendants.
For the algorithm, I would recommend Dijkstra's algorithm. Dijkstra's finds the shortest path from a starting node to all other nodes in a weighted graph. We can assign each generation a "weight" of 1, so it finds the closest living descendant. It's efficient, running in O(VlogV+E) time which should be fast enough for a family tree. Using Dijkstra's takes advantage of the graph representation and efficiently solves the problem of finding the closest living relative.Graph traversals in Data Structures



Graph traversals in Data StructuresAnandhasilambarasan D
╠²
Graph traversal techniques are used to search vertices in a graph and determine the order to visit vertices. There are two main techniques: breadth-first search (BFS) and depth-first search (DFS). BFS uses a queue and visits the nearest vertices first, producing a spanning tree. DFS uses a stack and visits vertices by going as deep as possible first, also producing a spanning tree. Both techniques involve marking visited vertices to avoid loops.graphtraversals.pdf



graphtraversals.pdfSeethaDinesh
╠²
This document discusses graph traversal techniques for searching graphs. It describes two common techniques: breadth-first search (BFS) and depth-first search (DFS). BFS uses a queue data structure to visit all adjacent vertices of the starting vertex before moving to the next level, producing a spanning tree. DFS uses a stack, visiting all vertices reachable from the starting point before backtracking, also producing a spanning tree. The document outlines the step-by-step process for implementing BFS and DFS on a graph.uninformed search part 1.pptx



uninformed search part 1.pptxMUZAMILALI48
╠²
Uninformed search algorithms traverse a search space without any additional information about the state or structure. The document describes several uninformed search algorithms:
- Breadth-first search expands all nodes at the current search level before moving to the next level. It is complete but uses more memory.
- Depth-first search prioritizes exploring paths fully before backtracking. It uses less memory than breadth-first search but may get stuck in infinite loops.
- Depth-limited search limits the depth of depth-first search to avoid infinite paths, making it incomplete but avoiding excessive memory usage.Depth first Search.pptx



Depth first Search.pptxAleezaShakeel3
╠²
The document discusses depth first search (DFS), an algorithm for traversing or searching trees or graphs. It begins with an introduction to DFS, explaining that it explores edges out of the most recently discovered vertex as deep as possible before backtracking. It then provides pseudocode for the DFS algorithm and explains that it has a time complexity of O(V+E), where V is the number of vertices and E is the number of edges. Finally, it lists some applications of DFS such as cycle detection, solving mazes, and analyzing networks.uniformed (also called blind search algo)



uniformed (also called blind search algo)ssuser2a76b5
╠²
The document discusses various uninformed (blind) search strategies: breadth-first search, uniform-cost search, depth-first search, and iterative deepening search. It provides information on the properties of each strategy, including completeness, time complexity, space complexity, and optimality. Iterative deepening search is generally preferred for uninformed searches as it has linear space complexity like depth-first search but is complete unlike depth-first search. Bidirectional search is preferred when applicable as it can reduce the search space in half.2012wq171-03-UninformedSeknlk ;lm,l;mk;arch.ppt



2012wq171-03-UninformedSeknlk ;lm,l;mk;arch.pptmmpnair0
╠²
The document discusses various uninformed (blind) search strategies: breadth-first search, uniform-cost search, depth-first search, and iterative deepening search. It provides information on the properties of each strategy, including completeness, time and space complexity, and optimality. Iterative deepening search is generally preferred for uninformed searches as it has linear space complexity like depth-first search but is complete unlike depth-first search. Bidirectional search is preferred when applicable as it can reduce the search space in half.Artificial Intelligence Problem Slaving PPT



Artificial Intelligence Problem Slaving PPTvipulkondekar
╠²
Artificial Intelligence Problem Slaving PPTBFS,DFS,Depth bound,Beam search,Iterative.pptx



BFS,DFS,Depth bound,Beam search,Iterative.pptxPriyadharshiniG41
╠²
BFS,DFS,Depth bound,Beam search,Iterative.pptxAnalysis of Pathfinding Algorithms



Analysis of Pathfinding AlgorithmsSigSegVSquad
╠²
An overview of the most simple algorithms used in data structures for path finding. Dijkstra, Breadth First Search, Depth First Search, Best First Search and A-star
Naturally feel free to copy for assignments and all ’śē Presentation on the artificial intelligenc



Presentation on the artificial intelligencPriyadharshiniG41
╠²
Presentation on the artificial intelligenc2.5 bfs & dfs 02



2.5 bfs & dfs 02Krish_ver2
╠²
The document provides information on graph traversals including depth-first search (DFS) and breadth-first search (BFS). It explains that DFS uses a stack and visits nodes in a recursive, preorder manner. BFS uses a queue and visits nodes level-by-level starting from the root. Examples of DFS and BFS on sample graphs are given to illustrate the traversal order.Branch and Bound.pptx



Branch and Bound.pptxJoshipavanEdduluru1
╠²
Branch and bound is a method for systematically searching a solution space that uses bounding functions to avoid generating subtrees that do not contain an answer node. It has a branching function that determines the order of exploring nodes and a bounding function that prunes the search tree efficiently. Branch and bound refers to methods where all children of the current node are generated before exploring other nodes. It generalizes breadth-first and depth-first search strategies. The method uses estimates of node costs and upper bounds to prune portions of the search space that cannot contain optimal solutions.3-uninformed-search.ppt



3-uninformed-search.pptABINASHACHERJEE1
╠²
The document discusses various algorithms for uninformed search. It covers breadth-first search, depth-first search, iterative deepening search, bidirectional search, and uniform cost search. Breadth-first search explores the shallowest nodes first and has optimal path length but exponential space complexity. Depth-first search uses less space but may reexplore nodes and not find optimal solutions. Iterative deepening search combines benefits of breadth-first and depth-first search. Bidirectional search simultaneously explores from start and goal nodes to meet in the middle. Uniform cost search prioritizes expanding lowest-cost nodes.Bfs present



Bfs presentminhaz uddin
╠²
Breadth First Search (BFS) is an algorithm for traversing or searching tree and graph data structures by exploring neighboring nodes first before moving to the next level neighbors. It works by assigning levels to nodes starting from the root node as level 0 and then exploring each level in order, marking visited nodes and placing unvisited children in the queue to be explored next.Airport Components Part1 ppt.pptx-Site layout,RUNWAY,TAXIWAY,TAXILANE



Airport Components Part1 ppt.pptx-Site layout,RUNWAY,TAXIWAY,TAXILANEPriyanka Dange
╠²
RUNWAY,TAXIWAY,TAXILANEMore Related Content
Similar to Breadth First Search with example and solutions (20)
Final slide4 (bsc csit) chapter 4



Final slide4 (bsc csit) chapter 4Subash Chandra Pakhrin
╠²
The document describes various search algorithms used to solve pathfinding problems represented as graphs. It discusses uninformed searches like breadth-first search (BFS) and depth-first search (DFS) as well as methods for evaluating search performance in terms of completeness, time complexity, space complexity, and optimality. BFS uses a queue to expand shallow nodes first, guaranteeing an optimal solution but with exponential time and space costs. DFS uses a stack to expand deep nodes first, providing better space efficiency but not guaranteeing an optimal solution.RPT_AI_03_PartB_UNINFORMED_FINAL.pptx



RPT_AI_03_PartB_UNINFORMED_FINAL.pptxRahulkumarTivarekar1
╠²
Iterative deepening search is an uninformed search strategy that combines the benefits of depth-first and breadth-first search. It gradually increases the depth limit in iterations, starting from 0, until a goal is found. This occurs when the depth limit reaches the depth of the shallowest goal node. Iterative deepening search is optimal, complete, and has reasonable time and space complexities. It is suitable for problems with large search spaces where the solution depth is unknown.Lecture 16 - Dijkstra's Algorithm.pdf



Lecture 16 - Dijkstra's Algorithm.pdfiftakhar8
╠²
For the family tree data structure, I would recommend using a graph represented by an adjacency list. This allows easy traversal of the connections between ancestors and descendants.
For the algorithm, I would recommend Dijkstra's algorithm. Dijkstra's finds the shortest path from a starting node to all other nodes in a weighted graph. We can assign each generation a "weight" of 1, so it finds the closest living descendant. It's efficient, running in O(VlogV+E) time which should be fast enough for a family tree. Using Dijkstra's takes advantage of the graph representation and efficiently solves the problem of finding the closest living relative.Graph traversals in Data Structures



Graph traversals in Data StructuresAnandhasilambarasan D
╠²
Graph traversal techniques are used to search vertices in a graph and determine the order to visit vertices. There are two main techniques: breadth-first search (BFS) and depth-first search (DFS). BFS uses a queue and visits the nearest vertices first, producing a spanning tree. DFS uses a stack and visits vertices by going as deep as possible first, also producing a spanning tree. Both techniques involve marking visited vertices to avoid loops.graphtraversals.pdf



graphtraversals.pdfSeethaDinesh
╠²
This document discusses graph traversal techniques for searching graphs. It describes two common techniques: breadth-first search (BFS) and depth-first search (DFS). BFS uses a queue data structure to visit all adjacent vertices of the starting vertex before moving to the next level, producing a spanning tree. DFS uses a stack, visiting all vertices reachable from the starting point before backtracking, also producing a spanning tree. The document outlines the step-by-step process for implementing BFS and DFS on a graph.uninformed search part 1.pptx



uninformed search part 1.pptxMUZAMILALI48
╠²
Uninformed search algorithms traverse a search space without any additional information about the state or structure. The document describes several uninformed search algorithms:
- Breadth-first search expands all nodes at the current search level before moving to the next level. It is complete but uses more memory.
- Depth-first search prioritizes exploring paths fully before backtracking. It uses less memory than breadth-first search but may get stuck in infinite loops.
- Depth-limited search limits the depth of depth-first search to avoid infinite paths, making it incomplete but avoiding excessive memory usage.Depth first Search.pptx



Depth first Search.pptxAleezaShakeel3
╠²
The document discusses depth first search (DFS), an algorithm for traversing or searching trees or graphs. It begins with an introduction to DFS, explaining that it explores edges out of the most recently discovered vertex as deep as possible before backtracking. It then provides pseudocode for the DFS algorithm and explains that it has a time complexity of O(V+E), where V is the number of vertices and E is the number of edges. Finally, it lists some applications of DFS such as cycle detection, solving mazes, and analyzing networks.uniformed (also called blind search algo)



uniformed (also called blind search algo)ssuser2a76b5
╠²
The document discusses various uninformed (blind) search strategies: breadth-first search, uniform-cost search, depth-first search, and iterative deepening search. It provides information on the properties of each strategy, including completeness, time complexity, space complexity, and optimality. Iterative deepening search is generally preferred for uninformed searches as it has linear space complexity like depth-first search but is complete unlike depth-first search. Bidirectional search is preferred when applicable as it can reduce the search space in half.2012wq171-03-UninformedSeknlk ;lm,l;mk;arch.ppt



2012wq171-03-UninformedSeknlk ;lm,l;mk;arch.pptmmpnair0
╠²
The document discusses various uninformed (blind) search strategies: breadth-first search, uniform-cost search, depth-first search, and iterative deepening search. It provides information on the properties of each strategy, including completeness, time and space complexity, and optimality. Iterative deepening search is generally preferred for uninformed searches as it has linear space complexity like depth-first search but is complete unlike depth-first search. Bidirectional search is preferred when applicable as it can reduce the search space in half.Artificial Intelligence Problem Slaving PPT



Artificial Intelligence Problem Slaving PPTvipulkondekar
╠²
Artificial Intelligence Problem Slaving PPTBFS,DFS,Depth bound,Beam search,Iterative.pptx



BFS,DFS,Depth bound,Beam search,Iterative.pptxPriyadharshiniG41
╠²
BFS,DFS,Depth bound,Beam search,Iterative.pptxAnalysis of Pathfinding Algorithms



Analysis of Pathfinding AlgorithmsSigSegVSquad
╠²
An overview of the most simple algorithms used in data structures for path finding. Dijkstra, Breadth First Search, Depth First Search, Best First Search and A-star
Naturally feel free to copy for assignments and all ’śē Presentation on the artificial intelligenc



Presentation on the artificial intelligencPriyadharshiniG41
╠²
Presentation on the artificial intelligenc2.5 bfs & dfs 02



2.5 bfs & dfs 02Krish_ver2
╠²
The document provides information on graph traversals including depth-first search (DFS) and breadth-first search (BFS). It explains that DFS uses a stack and visits nodes in a recursive, preorder manner. BFS uses a queue and visits nodes level-by-level starting from the root. Examples of DFS and BFS on sample graphs are given to illustrate the traversal order.Branch and Bound.pptx



Branch and Bound.pptxJoshipavanEdduluru1
╠²
Branch and bound is a method for systematically searching a solution space that uses bounding functions to avoid generating subtrees that do not contain an answer node. It has a branching function that determines the order of exploring nodes and a bounding function that prunes the search tree efficiently. Branch and bound refers to methods where all children of the current node are generated before exploring other nodes. It generalizes breadth-first and depth-first search strategies. The method uses estimates of node costs and upper bounds to prune portions of the search space that cannot contain optimal solutions.3-uninformed-search.ppt



3-uninformed-search.pptABINASHACHERJEE1
╠²
The document discusses various algorithms for uninformed search. It covers breadth-first search, depth-first search, iterative deepening search, bidirectional search, and uniform cost search. Breadth-first search explores the shallowest nodes first and has optimal path length but exponential space complexity. Depth-first search uses less space but may reexplore nodes and not find optimal solutions. Iterative deepening search combines benefits of breadth-first and depth-first search. Bidirectional search simultaneously explores from start and goal nodes to meet in the middle. Uniform cost search prioritizes expanding lowest-cost nodes.Bfs present



Bfs presentminhaz uddin
╠²
Breadth First Search (BFS) is an algorithm for traversing or searching tree and graph data structures by exploring neighboring nodes first before moving to the next level neighbors. It works by assigning levels to nodes starting from the root node as level 0 and then exploring each level in order, marking visited nodes and placing unvisited children in the queue to be explored next.Recently uploaded (20)
Airport Components Part1 ppt.pptx-Site layout,RUNWAY,TAXIWAY,TAXILANE



Airport Components Part1 ppt.pptx-Site layout,RUNWAY,TAXIWAY,TAXILANEPriyanka Dange
╠²
RUNWAY,TAXIWAY,TAXILANESelf-Compacting Concrete: Composition, Properties, and Applications in Modern...



Self-Compacting Concrete: Composition, Properties, and Applications in Modern...NIT SILCHAR
╠²
Self-Compacting Concrete (SCC) is a high-performance material that flows under its own weight, eliminating the need for vibration. It offers superior workability, durability, and structural efficiency, making it ideal for complex designs, congested reinforcement, and sustainable construction practices.PCB Design - Top Factors Related to Data Routing and Layout



PCB Design - Top Factors Related to Data Routing and LayoutEpec Engineered Technologies
╠²
When it comes to PCB design and layout, the decisions made early in your project can significantly impact not only the functionality of your circuit board but also its manufacturability, cost, and lead time. Understanding these critical considerations helps ensure a seamless transition from design to production while avoiding costly errors or delays.
Key factors to address include material selection, maximum board thickness, layer count, and whether to incorporate advanced features like blind and buried vias.
Additionally, considerations around copper weights, trace widths and spacing, balanced copper distribution, and overall design complexity can heavily influence both manufacturability and reliability.
A crucial question is: When should you involve your PCB provider in the design process?
Engaging early can help identify potential roadblocks, ensure design-for-manufacturing (DFM) compatibility, and optimize your layout for efficient production.
In this webinar, we take a deep dive into PCB designs as they relate to manufacturing.
Whether youŌĆÖre developing a simple two-layer board or a complex multilayer design, this session will provide actionable insights to streamline your process and achieve the best results for your project.
For more information on our PCB solutions, visit https://www.epectec.com/pcb.Intro of Airport Engg..pptx-Definition of airport engineering and airport pla...



Intro of Airport Engg..pptx-Definition of airport engineering and airport pla...Priyanka Dange
╠²
Definition of airport engineering and airport planning, Types of surveys required for airport site, Factors affecting the selection of site for AirportKamal 2, new features and practical examples



Kamal 2, new features and practical examplesIgor Aleksandrov
╠²
║▌║▌▀Żs about Kamal 2 features and some practical examples.
Showed live on the Tropical on Rails 2025, S├Żo Paulo, Brazil, April 4th, 2025.22PCOAM16 _ML_ Unit 2 Full unit notes.pdf



22PCOAM16 _ML_ Unit 2 Full unit notes.pdfGuru Nanak Technical Institutions
╠²
22 PCOAM16 _ML_ Unit 2 Full unit notes.pdfCS50x: CS50's Introduction to Computer Science.pdf



CS50x: CS50's Introduction to Computer Science.pdfNaiyan Noor
╠²
CS50x: CS50's Introduction to Computer Science is Harvard University's free online entry-level course that teaches the fundamentals of computer science and programming. It covers key topics like algorithms, data structures, web development, and more, using languages such as C, Python, and JavaScript. The course is known for its engaging lectures, hands-on problem sets, and real-world projects, making it ideal for beginners with no prior experience.Industry 4.0: Transforming Modern Manufacturing and Beyond



Industry 4.0: Transforming Modern Manufacturing and BeyondGtxDriver
╠²
This document explores the fundamental concepts, technologies, and applications of Industry 4.0. Topics include automation, IoT (Internet of Things), smart factories, cyber-physical systems, and the integration of AI and big data analytics in industrial processes. It serves as a comprehensive resource for students, professionals, and enthusiasts eager to delve into the fourth industrial revolution.Mastering Secure Login Mechanisms for React Apps.pdf



Mastering Secure Login Mechanisms for React Apps.pdfBrion Mario
╠²
How to securely add login to any React application.Mix Design of M40 Concrete & Application of NDT.pptx



Mix Design of M40 Concrete & Application of NDT.pptxnarayan311979
╠²
This presentation briefs the audience about how to carry out design mix of M40 concrete, what are the cares one need to take while doing trials. Second part of presentation deals with various NDT test and its applications in evaluating quality of concrete of existing structures. BSS_1_E1.2_ElectromobilityElectromobility.pdf



BSS_1_E1.2_ElectromobilityElectromobility.pdfjungdan064
╠²
Electromobility, or e-mobility, refers to the use of electric powertrain technologies, in-vehicle information, and communication technologies, and connected infrastructure to enable electric vehicles (EVs) and reduce dependence on fossil fuels. As the world faces increasing environmental challenges such as climate change, air pollution, and the depletion of natural resources, electromobility has emerged as a promising solution for sustainable transportation.
At the heart of electromobility are electric vehicles, which include battery electric vehicles (BEVs), plug-in hybrid electric vehicles (PHEVs), and fuel cell electric vehicles (FCEVs). These vehicles use electricity either stored in batteries or generated through hydrogen fuel cells, drastically reducing or even eliminating tailpipe emissions. Compared to internal combustion engine (ICE) vehicles, EVs have significantly lower greenhouse gas emissions over their lifecycle, especially when powered by renewable energy sources like wind or solar.
One of the primary drivers of the electromobility revolution is the urgent need to decarbonize transportation. The transport sector contributes nearly one-quarter of global COŌéé emissions, with road vehicles being the largest contributors. Transitioning to electric vehicles helps countries meet their climate goals under international agreements such as the Paris Accord. Furthermore, cities struggling with air pollution see electromobility as a way to improve public health by reducing harmful pollutants like nitrogen oxides and particulate matter.
In addition to environmental benefits, electromobility offers economic advantages. EVs have lower operating and maintenance costs due to fewer moving parts and greater energy efficiency. Governments around the world have supported this shift by offering subsidies, tax incentives, and investing in charging infrastructure. The development of fast-charging networks and home-charging solutions has made EV ownership more convenient than ever before.
Technological advancements in battery chemistry, such as lithium-ion and solid-state batteries, are improving driving range and reducing charging time. At the same time, smart charging systems and vehicle-to-grid (V2G) technologies are integrating EVs into the broader energy ecosystem. In V2G systems, EVs can feed electricity back into the grid during peak demand periods, creating a more resilient and balanced power network.
Electromobility extends beyond private passenger cars. It includes electric buses, trucks, bikes, scooters, and even ferries and airplanes. Public transportation authorities are increasingly adopting electric buses to reduce emissions and noise in urban areas. E-bikes and scooters provide convenient, zero-emission alternatives for short-distance travel, supporting the development of ŌĆ£last mileŌĆØ mobility solutions.
22PCOAM16 ML UNIT 2 NOTES & QB QUESTION WITH ANSWERS



22PCOAM16 ML UNIT 2 NOTES & QB QUESTION WITH ANSWERSGuru Nanak Technical Institutions
╠²
22PCOAM16 ML UNIT 2 NOTES & QB QUESTION WITH ANSWERS Breadth First Search with example and solutions
- 1. BFS
- 2. Breadth-first search ’éŚ Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. ’éŚ It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a ŌĆśsearch keyŌĆÖ), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level. ’éŚ It is implemented using a queue(FIFO). ’éŚ BFS traverses the tree ŌĆ£shallowest node firstŌĆØ, it would always pick the shallower branch until it reaches the solution (or it runs out of nodes, and goes to the next branch).
- 3. Algorithm 3 ’éŚ Declare a queue and insert the starting vertex. ’éŚ Initialize a visited array and mark the starting vertex as visited. ’éŚ Follow the below process till the queue becomes empty: ’éŚ Remove the first vertex of the queue. ’éŚ Mark that vertex as visited. ’éŚ Insert all the unvisited neighbors of the vertex into the queue.
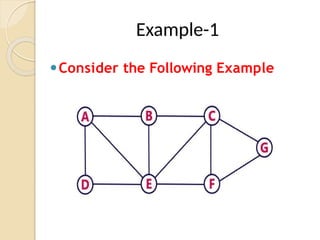
- 4. ŌܽConsider the Following Example Example-1
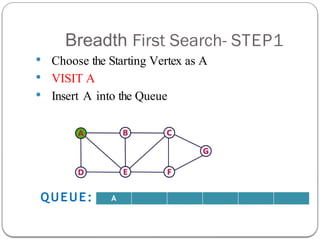
- 5. Breadth First Search- STEP1 ’éŚ Choose the Starting Vertex as A ’éŚ VISIT A ’éŚ Insert A into the Queue A QUEUE:
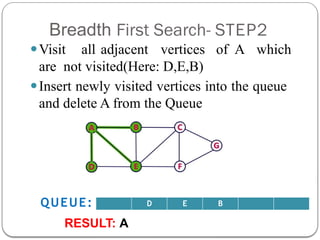
- 6. Breadth First Search- STEP2 ŌܽVisit all adjacent vertices of A which are not visited(Here: D,E,B) ŌܽInsert newly visited vertices into the queue and delete A from the Queue D E B QUEUE: RESULT: A
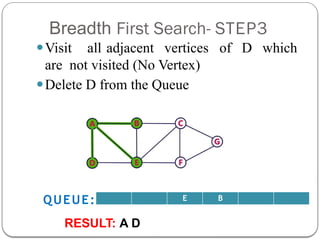
- 7. Breadth First Search- STEP3 ŌܽVisit all adjacent vertices of D which are not visited (No Vertex) ŌܽDelete D from the Queue E B QUEUE: RESULT: A D
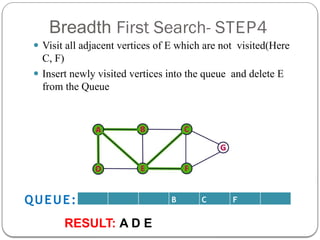
- 8. Breadth First Search- STEP4 Ōܽ Visit all adjacent vertices of E which are not visited(Here C, F) Ōܽ Insert newly visited vertices into the queue and delete E from the Queue B C F QUEUE: RESULT: A D E
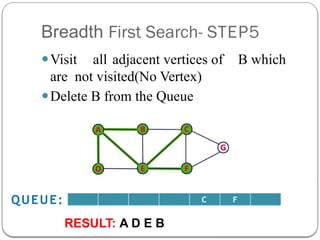
- 9. Breadth First Search- STEP5 ŌܽVisit all adjacent vertices of B which are not visited(No Vertex) ŌܽDelete B from the Queue C F QUEUE: RESULT: A D E B
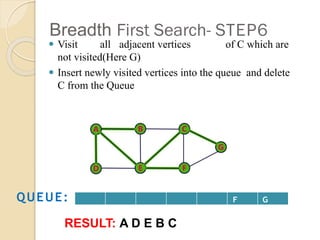
- 10. Breadth First Search- STEP6 Ōܽ Visit all adjacent vertices of C which are not visited(Here G) Ōܽ Insert newly visited vertices into the queue and delete C from the Queue F G QUEUE: RESULT: A D E B C
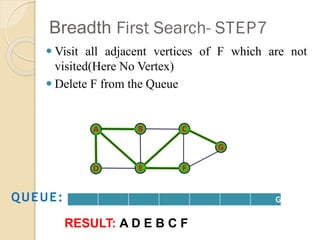
- 11. Breadth First Search- STEP7 Ōܽ Visit all adjacent vertices of F which are not visited(Here No Vertex) Ōܽ Delete F from the Queue G QUEUE: RESULT: A D E B C F
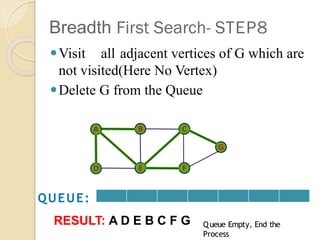
- 12. Breadth First Search- STEP8 ŌܽVisit all adjacent vertices of G which are not visited(Here No Vertex) ŌܽDelete G from the Queue QUEUE: Queue Empty, End the Process RESULT: A D E B C F G
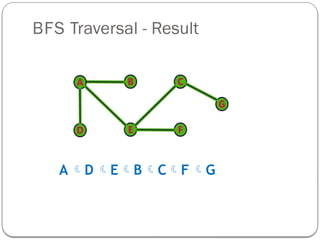
- 13. BFS Traversal - Result A’āĀD ’āĀE’āĀB’āĀC’āĀF ’āĀG
- 14. 14 Advantages ŌĆó BFS will provide a solution if any solution exists. ŌĆó If there are more than one solution for a given problem, then BFS will provide minimum solution which requires the least number of steps. Disadvantage ŌĆó It requires lot of memory since each level of the tree must be saved into memory to expand the next level. ŌĆó BFS needs lot of time if the solution is far a way from the root.
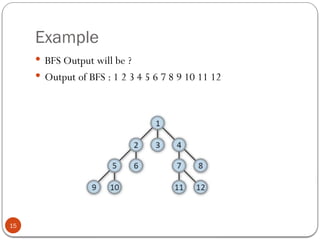
- 15. Example 15 ’éŚ BFS Output will be ? ’éŚ Output of BFS : 1 2 3 4 5 6 7 8 9 10 11 12
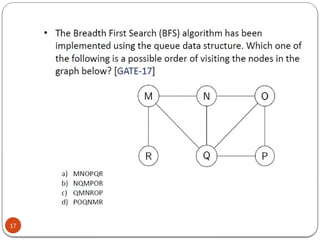
- 16. 16
- 17. 17
- 19. 19 Time complexity: Equivalent to the number of nodes traversed in BFS until the shallowest solution. T(n) = 1 + n^2 + n^3 + ... + n^s = O(n^s) ŌĆó s = the depth of the shallowest solution. ŌĆó n^i = number of nodes in level i. Space complexity: Equivalent to how large can the fringe get. S(n) = O(n^s)
- 20. 20 ŌĆó Completeness: BFS is complete, meaning for a given search tree, BFS will come up with a solution if it exists. ŌĆó Optimality: BFS is optimal as long as the costs of all edges are equal.
- 21. 21
- 22. 22
- 23. 23












