狠狠撸

CHAPTER 11
NULL HYPOTHESIS
SIGNIFICANCE TESTING
Hiroki Takanashi
(takanashi@r.recruit.co.jp)

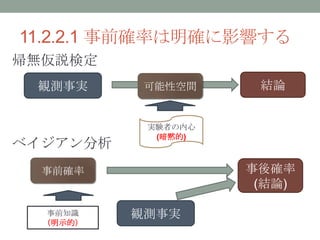
本章のサマリ
? NHST(帰無仮説検定)とベイジアン分析との対比を説明
? 新しい手法の提示はでなく、帰無仮説検定の問題点の提示と、
ベイジアン分析が優れている理由を述べている章
★帰無仮説検定の問題点
データの解釈が実験者の「意図 (内心)」でに依存するた
め、対象とする可能性空間の設定方法次第で、検定結果が変わ
る
実験者がデータを逐次みながら検定を考えることで、本来
の検定結果よりも有意度が高く出てしまう（false alarm)
★ベイジアン分析が優れている点
事後確率(posterior)の分析が全てなので、実験者の意図によっ
てデータの解釈が変わることがない。
観測対象に対する知識などを事前確率(priterior)に含める、明
らかな議論となるので、実験者の「内心」には関係しない

【導入】帰無仮説検定とベイジアン
分析
ベイジアン分析は、伝統的な帰無仮説検定
(NHST)と対応させることができる。具体的
には以下の問題を例として２つを比較す
る。
問題
“２６回コインを投げて８回表が出
た。このコインは偏っているか？”

【導入】帰無仮説検定の問題
? NHSTの結果は、実験者の意図（内心）に
左右される。
? 観測結果は同じN=26、z=8でも
? ①N=26となるように投げた（つもり）
? ②z=8となるように投げた（つもり）
? ③1分間投げ続けた（つもり）
によって、NHSTの際に設定する可能性空
間が変わるため、検定(コインの公正さ)の
結論が変わってしまう

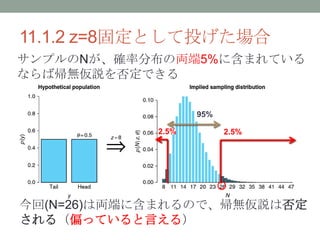
11.1 コインの偏りの帰無仮説検定
? 「コインが偏っている」ことの帰無仮説検
定
コインが偏っていることに対する帰無仮説
“コインは偏っていない(θ=0.5)”
を一定の有意水準(ex. 5%)で棄却できれ
ば、
「コインは偏っている(だろう」と言える。

11.1.1 N=26固定として投げた場合
N回コインを投げて、z回表になる確
率
θ=0.5としたときの、確率分布

11.1.1 N=26固定として投げた場合
2.5% 2.5%
サンプルのzが、確率分布の両端5%に含まれている
ならば帰無仮説を否定できる
95%
今回(z=8)は両端に含まれないので、帰無仮説は否
定されない（偏っているとは言えない）

11.1.2 z=8固定として投げた場合
z回表がでるまでにN回コインを投げる確
率
θ=0.5としたときの、確率分布

11.1.2 z=8固定として投げた場合
2.5% 2.5%
サンプルのNが、確率分布の両端5%に含まれている
ならば帰無仮説を否定できる
95%
今回(N=26)は両端に含まれるので、帰無仮説は否定
される（偏っていると言える）

11.1.3 “内心”の詮索
? 観測結果は同じN=26、z=8でも
? ①N=26となるように投げた（つもり）
? →帰無仮説が否定されなかった（コイ
ンが偏ってるとは言えない）
? ②z=8となるように投げた（つもり）
? →帰無仮説が否定された（コインが
偏っていると言える）
? NHSTの結果は、実験者の意図（内心）
に左右されてしまっている。（よろしく
ない）

11.1.3 “内心”の詮索
? 実際の環境では実験者は”予備的な”データ
収集を行って、データを観察する
? ①現在集まっているデータに対して帰無仮説検
定を実施
? ②有意な結果が得られたら終了、有意でなけれ
ばデータをさらに集めて①を繰り返す
?このような操作を行うと、有意水準を5%
としても、誤って有意だと判定する(false
alarm)可能性はそれ以上に上がる

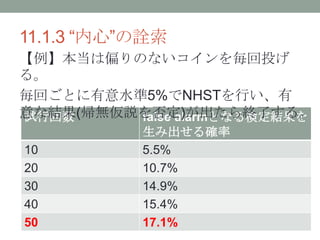
11.1.3 “内心”の詮索
試行回数 false alarmとなる検定結果を
生み出せる確率
10 5.5%
20 10.7%
30 14.9%
40 15.4%
50 17.1%
【例】本当は偏りのないコインを毎回投げ
る。
毎回ごとに有意水準5%でNHSTを行い、有
意な結果(帰無仮説を否定)が出たら終了する。

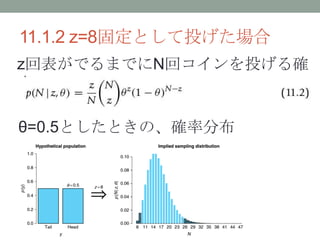
11.1.4 ベイジアン分析
? ベイジアン分析では、観測されたデータの
みを扱う。NHSTのように(未観測の)”可能
性の空間”を仮定することはない。
? よって、ベイジアン分析では、データの解
釈が実験者の主観に依存することはない。
? N回コインを投げた時z回表がでる尤度
(likelihood)は常に

11.2 観測対象に対する事前知識
【例】コインではなく釘を投げる場合
?釘が表（立った状態）になりづらい、
という事前知識を実験者は持っている
?「釘が公正か？」を検定したい
釘が「立ったら」表

11.2.1 帰無仮説検定
? 帰無仮説検定では、コインの性質（表が出
やすいなど）に対する事前知識を含められ
ない
? 釘を26回投げて8回表が出た場合も、「釘
が偏っていない(θ=0.5)と言えなかった」と
いう検定結果しか主張できない。

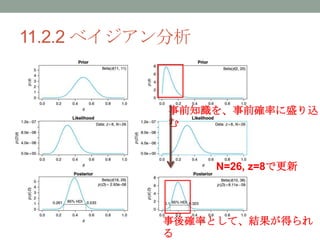
? ベイジアン分析であれば、「釘は表になり
にくい」という事前知識を事前確率(prior)
に含めることができる
? Ex) 20回投げて2回しか表が出そうにない
? ? beta(θ | 2, 20) を事前確率として用い
る
この事前確率を、N=26、z=8で更新
する。

事前知識を、事前確率に盛り込
む
事後確率として、結果が得られ
る
N=26, z=8で更新

11.2.2.1 事前確率は明確に影響する
帰無仮説検定
観測事実結論可能性空間
実験者の内心
(暗黙的)
ベイジアン分析
事前確率
事前知識
（明示的）
観測事実
事後確率
(結論)

11.3 信頼区間とHDI
? 信頼区間＝変数(θ)が、一定の有意水準に
おける帰無仮説で棄却されない区間
? 帰無仮説検定における信頼区間
(confidence interval)と、ベイジアン分析
のHDI(highest density interval)が対応す
る。
? 帰無仮説検定では、前節と同様に実験者
の意図（内心）によって、信頼区間の値
(結論)が変わってしまう。

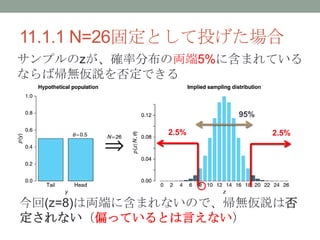
11.3.1 NHSTの信頼区間
?N=26固定としてzを確率変数と考えた
時。
?θに対する5%有意水準での信頼区間は
θ∈ [0.144, 0.517]
0.144 0.517
棄却される棄却される
帰無仮説検定で棄却され
ない区間
θ

N=26固定でzを確率変数と見た時。
θ∈ [0.144, 0.517]

z=9固定としてNを確率変数と考えた時。
θ∈ [0.144, 0.493]

? 同じN=26、z=8の観測結果に対して
? ①N=26固定としてzを確率変数と考えた
時。
? ?信頼区間はθ∈ [0.144, 0.517]
? ②z=8固定としてNを確率変数と考えた
時。
? ?信頼区間はθ∈ [0.144, 0.493]
? 実験者の意図（内心）によって、同じ変数

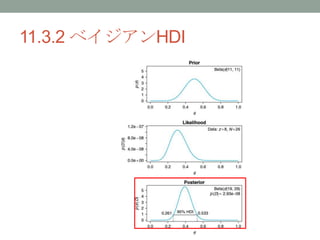
11.3.2 ベイジアンHDI
? 設定した事前確率beta(θ | 11, 11)に対して、
N=26、z=8の観測結果を得た後の事後確率
が必ず１つ定まる。
? ここから95% HDI
? θ∈ [0.261, 0.533]が求まる。
? 実験者の意図（内心）は影響しない

11.3.2 ベイジアンHDI
?HDIの信頼区間に対する利点
?①HDIはθの分布p(θ | D)を直接表現でき
る（NHSTの信頼区間は、θの分布には
直接関係がない)
?②HDIは事前確率と観測事実のみに基
づき、実験者の意図（内心）に対して
一切依存しない
?③HDIには事前知識が計算に反映され
る

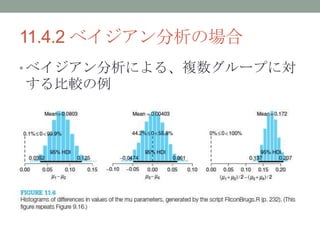
11.4 複数の比較
? 複数のグループ(条件)を比較する場合におい
ても、帰無仮説検定とベイジアン分析を対応
させられる。
? NHSTでは、グループ間の比較回数を増やす
ほど結論が誤り(false alarm)である確率(誤り
率)が上がる。
? NHSTで誤り率を一定以下に抑えるために
は、試行回数を制限することになるため、結
論が実験者の意図によって影響を受ける。
? ベイジアン分析では、パラメータに対する１
つの事後確率しか持たないので、そのような
実験者の意図の影響を受けない。

11.4.1 NHSTでの実験ごとの誤りの修正
? 例えば４つのグループがある場合、６通りの
組み合わせでNHSTを行うことができる。(全
てのグループでμが同じ、など）
? １回の検定での誤り率αPC=5%とすると、試行
回数c=6回検定を行った時の全体の誤り率αEW
は
? 仮に帰無仮説が正しかったとしても、26%
誤って棄却してしまう。

? 検定の回数cが増えるほど、全体の全体の
誤り率αEWは大きく増加する。
? ※）ただし、現実のケースでは全ての検定が独立ではな
い。この場合αEWの増加はcに対して抑えられる
? 全体としての誤り率を抑えるためには、１
回の検定での誤り率αPCを制約しなければ
ならない。
? 例）Bonferonni Correction

? 行うべき検定を実験者がデータを見る前に定
めていた(planned)か、データを見た後に決め
た(post hoc)かによって誤り率が変わる。
? Post hocの場合、実験者がデータが有意であ
るケースのみ検定することで、誤って有意と
言ってしまう確率が増幅される。
? ※NHSTでの複数グループに対する検定で
は、試行回数cの数で全体の誤り率が修正され
るため、試行する検定をデータを見た後に選
ぶことは、誤り率の操作になる。
? データを注意深く見て、仮説を定めること自
体に対してペナルティが働いてしまう矛盾

11.4.2 ベイジアン分析の場合
? ベイジアン分析の場合、事前確率と観測事
実のみによって計算されるため、事後確率
は一意に定まる。
? 観測者の意図によって、データの解釈が影
響される余地がない。
? 複数グループの比較する場合は、各パラ
メータの和差(ex. μi - μｊ）についての事後
確率の分布を求めることになる。

11.4.2 ベイジアン分析の場合
? ベイジアン分析による、複数グループに対
する比較の例

11.4.3 ベイジアン分析における誤りの緩
和
? どのような分析方法であっても、誤りの可
能性を含むことになる
? ベイジアン分析においては、事前知識を事
前確率に含めることで誤り率を緩和できる
と考える
? グループ全体に対して、何らかの共通性な
どがあれば、それを事前確率の分布のモデ
ルにあらかじめ含めておくことができる。

11.5 標本分布の有効性
? 帰無仮説検定で用いる標本分布は、ベイジ
アン分析の事後確率分布ほど役には立たな
い（※筆者の主張）
? なぜなら、標本分布で用いる、可能性の空
間は特定の仮説に依存し、複数の仮説の可
能性を考慮できないため。
? ただし、標本分布を利用することが適切な
ケースもある。

11.5.1 実験の計画
? 実際のデータを集める前に、ベイジアン分
析で必要な精度のHDIを得るためのサンプ
ルサイズを計算する。
? 例えば、θ=0.60であるという仮説をベイジ
アン分析を用いて検証するうえで、z=100
のサンプルサイズで十分か、仮の標本集合
を作ってあてはめてみて検証する。

11.5.2 モデルの予測性の検討
(事後確率の予測性のチェック）
? 事後確率はパラメータが悪くない範囲のみ
を示す（もっとも“悪くない”パラメータの
値が、実際に適切か、までは言えない）
? 【例】99%裏表モデル
? ①θ=0.99、②θ=0.01、の２つのモデルがを考え
る。
? N=40、z=30の観測事実に対して事後確率を計
算することで①のほうが望ましいとわかる。
? ①に従った事後確率分布がN=40、z=30の観測
事実について本当に適切かは別の問題。

11.5.2 モデルの予測性の検討
(事後確率の予測性のチェック）
? 実際に事後確率パラメータが有効かをチェッ
クするために、事後確率予測性チェック
(posterior predictive check)を行う。
? 事後確率パラメータから予測された結果が、
実データに”似ていた”場合、そのパラメータ
（モデル）が適切だと判断できる。
? パラメータを使って、結果の予測と実データ
との比較を繰り返すことはNHSTとよく似て
いる。
? モデルの標本空間のどこに実データが入るか
をみることになる。（誤り率に対する許容値
を定められば直接NHSTになる）

狠狠撸

Doing Bayesian Data Analysis Chapter 11. Null Hypothesis Significance Testing

More Related Content

What's hot (15)

Viewers also liked (17)

Doing Bayesian Data Analysis Chapter 11. Null Hypothesis Significance Testing