Chapter13.2.3
- 1. Ą┌16╗žPRMLšiĢ°╗ß ░k▒Ē┘Y┴Ž 13.2.3 HMMż╬Ęe║═źóźļź┤źĻź║źÓ 2010/07/17 Presented by takmin
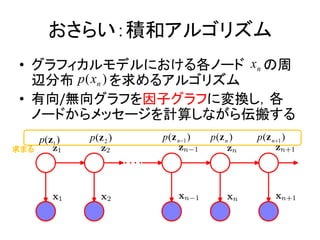
- 2. ż│ż╬š┬żŪčįżżż┐żżż│ż╚ ? Ęe║═źóźļź┤źĻź║źÓżŪżŌźšź®ź’®`ź╔-źąź├ź»ź’®`ź╔ źóźļź┤źĻź║źÓż¼Ą╝│÷żŪżŁżļ
- 3. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ ? ź░źķźšźŻź½źļźŌźŪźļż╦ż¬ż▒żļĖ„ź╬®`ź╔ x n ż╬ų▄ ▐xĘų▓╝ p ( xn ) ż“Ū¾żßżļźóźļź┤źĻź║źÓ ? ėąŽ“/¤oŽ“ź░źķźšż“ę“ūėź░źķźšż╦ēõōQżĘŻ¼Ė„ ź╬®`ź╔ż½żķźßź├ź╗®`źĖż“ėŗ╦ѿʿ╩ż¼żķü╗░ßż╣żļ p(z1 ) p(z 2 ) p ( z n ?1 ) p(z n ) p ( z n ?1 ) Ū¾ż▐żļ
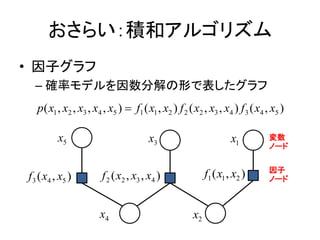
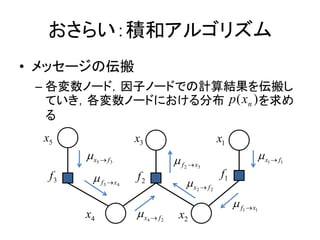
- 4. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ ? ę“ūėź░źķźš ©C ┤_┬╩źŌźŪźļż“ę“╩²ĘųĮŌż╬ą╬żŪ▒ĒżĘż┐ź░źķźš p( x1 , x2 , x3 , x4 , x5 ) ? f1 ( x1 , x2 ) f 2 ( x2 , x3 , x4 ) f 3 ( x4 , x5 ) x5 x3 x1 ēõ╩² ź╬®`ź╔ ę“ūė f 3 ( x4 , x5 ) f 2 ( x2 , x3 , x4 ) f1 ( x1 , x2 ) ź╬®`ź╔ x4 x2
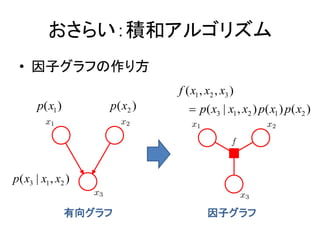
- 5. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ ? ę“ūėź░źķźšż╬ū„żĻĘĮ f ( x1 , x2 , x3 ) p( x1 ) p ( x2 ) ? p( x3 | x1 , x2 ) p( x1 ) p( x2 ) p( x3 | x1 , x2 ) ėąŽ“ź░źķźš ę“ūėź░źķźš
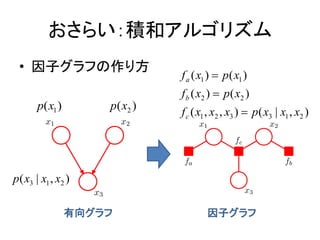
- 6. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ ? ę“ūėź░źķźšż╬ū„żĻĘĮ f a ( x1 ) ? p( x1 ) f b ( x2 ) ? p ( x 2 ) p( x1 ) p ( x2 ) f c ( x1 , x2 , x3 ) ? p( x3 | x1 , x2 ) p( x3 | x1 , x2 ) ėąŽ“ź░źķźš ę“ūėź░źķźš
- 7. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ ? źßź├ź╗®`źĖż╬ü╗░ß ©C Ė„ēõ╩²ź╬®`ź╔Ż¼ę“ūėź╬®`ź╔żŪż╬ėŗ╦ŃĮY╣¹ż“ü╗░ßżĘ żŲżżżŁŻ¼Ė„ēõ╩²ź╬®`ź╔ż╦ż¬ż▒żļĘų▓╝ p ( xn ) ż“Ū¾żß żļ x5 x3 x1 ?x ? f 5 3 ?f ?x ? f 1 1 2 ? x3 f3 ?f f2 f1 3 ? x4 ?x ? f 2 2 ? f ?x x4 ?x ? f 4 2 x2 1 1
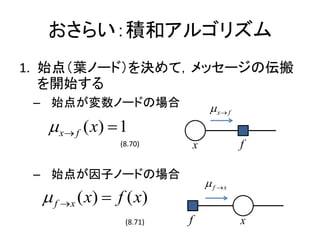
- 8. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ 1. ╩╝ĄŃŻ©╚~ź╬®`ź╔Ż®ż“øQżßżŲŻ¼źßź├ź╗®`źĖż╬ü╗░ß ż“ķ_╩╝ż╣żļ ©C ╩╝ĄŃż¼ēõ╩²ź╬®`ź╔ż╬ł÷║Ž ? x? f ? x ? f ( x) ? 1 (8.70) x f ©C ╩╝ĄŃż¼ę“ūėź╬®`ź╔ż╬ł÷║Ž ? f ?x ? f ? x ( x) ? f ( x) (8.71) f x
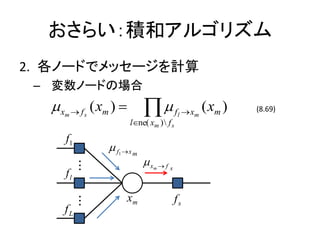
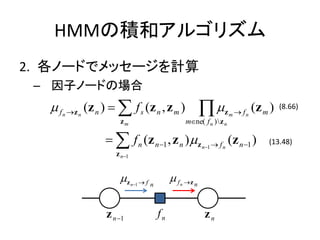
- 9. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ 2. Ė„ź╬®`ź╔żŪźßź├ź╗®`źĖż“ėŗ╦Ń ©C ēõ╩²ź╬®`ź╔ż╬ł÷║Ž ?x m ? fs ( xm ) ? ?? l?ne( xm ) f s f l ? xm ( xm ) (8.69) f1 ? f ?x m 1 ? ? ?x m? fs fl ? ? ? xm fs fL ?
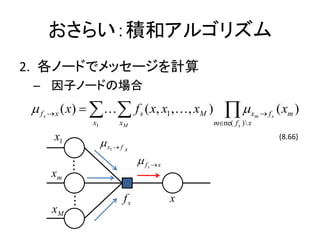
- 10. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ 2. Ė„ź╬®`ź╔żŪźßź├ź╗®`źĖż“ėŗ╦Ń ©C ę“ūėź╬®`ź╔ż╬ł÷║Ž ? f ? x ( x) ? ??? f s ( x, x1 ,?, xM ) s ?? xm ? f s ( xm ) x1 xM m?ne( f s ) x x1 (8.66) ?x ? f s 1 ? ? f ?x ? s xm ? ? ? fs x xM ?
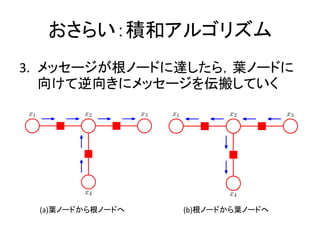
- 11. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ 3. źßź├ź╗®`źĖż¼Ė∙ź╬®`ź╔ż╦▀_żĘż┐żķŻ¼╚~ź╬®`ź╔ż╦ Ž“ż▒żŲ─µŽ“żŁż╦źßź├ź╗®`źĖż“ü╗░߿ʿŲżżż» (a)╚~ź╬®`ź╔ż½żķĖ∙ź╬®`ź╔żž (b)Ė∙ź╬®`ź╔ż½żķ╚~ź╬®`ź╔żž
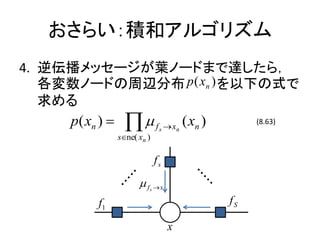
- 12. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ 4. ─µü╗▓źźßź├ź╗®`źĖż¼╚~ź╬®`ź╔ż▐żŪ▀_żĘż┐żķŻ¼ Ė„ēõ╩²ź╬®`ź╔ż╬ų▄▐xĘų▓╝ p ( xn ) ż“ęįŽ┬ż╬╩ĮżŪ Ū¾żßżļ p( xn ) ? ? ? f s ? xn ( xn ) (8.63) s?ne( xn ) fs ? f ?x s f1 fS x
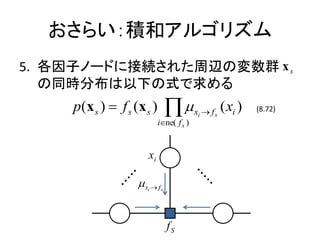
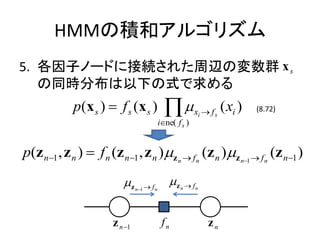
- 13. ż¬żĄżķżżŻ║Ęe║═źóźļź┤źĻź║źÓ 5. Ė„ę“ūėź╬®`ź╔ż╦ĮėŠAżĄżņż┐ų▄▐xż╬ēõ╩²╚║ x s ż╬═¼ĢrĘų▓╝żŽęįŽ┬ż╬╩ĮżŪŪ¾żßżļ p(x s ) ? f s (x s ) ?? i?ne( f s ) xi ? f s ( xi ) (8.72) xi ?x ? f i s fS
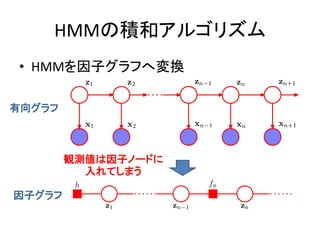
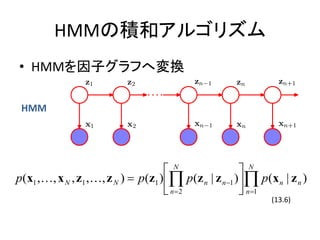
- 14. HMMż╬Ęe║═źóźļź┤źĻź║źÓ ? HMMż“ę“ūėź░źķźšżžēõōQ ėąŽ“ź░źķźš ėQ£yéÄżŽę“ūėź╬®`ź╔ż╦ ╚ļżņżŲżĘż▐ż” ę“ūėź░źķźš
- 15. HMMż╬Ęe║═źóźļź┤źĻź║źÓ ? HMMż“ę“ūėź░źķźšżžēõōQ HMM ?N ? N p(x1 ,?, x N , z1 ,?, z N ) ? p(z1 ) ?? p(z n | z n?1 )?? p(x n | z n ) ? n?2 ? n?1 (13.6)
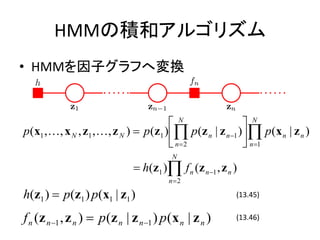
- 16. HMMż╬Ęe║═źóźļź┤źĻź║źÓ ? HMMż“ę“ūėź░źķźšżžēõōQ ? N ? N p(x1 ,?, x N , z1 ,?, z N ) ? p(z1 ) ?? p(z n | z n ?1 )?? p(x n | z n ) ? n?2 ? n ?1 N ? h(z1 )? f n (z n ?1 , z n ) n?2 h(z1 ) ? p(z1 ) p(x1 | z1 ) (13.45) f n (z n ?1 , z n ) ? p(z n | z n ?1 ) p (x n | z n ) (13.46)
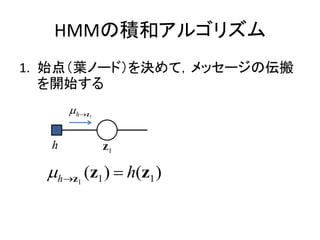
- 17. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 1. ╩╝ĄŃŻ©╚~ź╬®`ź╔Ż®ż“øQżßżŲŻ¼źßź├ź╗®`źĖż╬ü╗░ß ż“ķ_╩╝ż╣żļ ? h ?z 1 h z1 ?h?z (z1 ) ? h(z1 ) 1
- 18. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 1. ╩╝ĄŃŻ©╚~ź╬®`ź╔Ż®ż“øQżßżŲŻ¼źßź├ź╗®`źĖż╬ü╗░ß ż“ķ_╩╝ż╣żļ ©C źšź®ź’®`ź╔-źąź├ź»ź’®`ź╔źóźļź┤źĻź║źÓż╚ż╬▒╚▌^ Ęe║═źóźļź┤źĻź║źÓ ?h?z (z1 ) ? h(z1 ) ? p(z1 ) p(x1 | z1 ) 1 (13.45) ? (z1 ) ? ? f n ?z n (z1 ) źšź®ź’®`ź╔-źąź├ź»ź’®`ź╔źóźļź┤źĻź║źÓ ? (z1 ) ? p(z1 ) p(x1 | z1 ) (13.37)
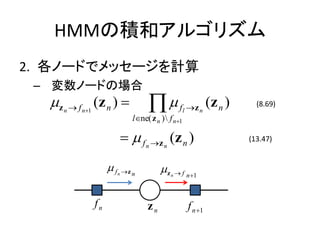
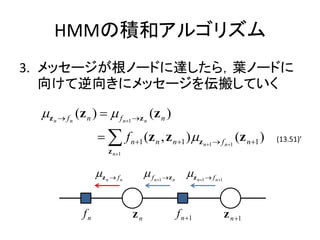
- 19. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 2. Ė„ź╬®`ź╔żŪźßź├ź╗®`źĖż“ėŗ╦Ń ©C ēõ╩²ź╬®`ź╔ż╬ł÷║Ž ?z n ? f n?1 (z n ) ? ?? f l ?z n l?ne( z n ) f n?1 (z n ) (8.69) ? ? f n ?z n ( z n ) (13.47) ?f n ?z n ?z n? f n ?1 fn zn f n ?1
- 20. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 2. Ė„ź╬®`ź╔żŪźßź├ź╗®`źĖż“ėŗ╦Ń ©C ę“ūėź╬®`ź╔ż╬ł÷║Ž ?f n ?z n (z n ) ? ? f s (z n , z m ) ?? zm ? fn (z m ) (8.66) zm m?ne( f n ) z n ? ? f n (z n ?1 , z n ) ? z n?1 ? f n (z n ?1 ) (13.48) z n?1 ?z n?1 ? f n ?f n ?z n z n ?1 fn zn
- 21. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 2. Ė„ź╬®`ź╔żŪźßź├ź╗®`źĖż“ėŗ╦Ń ēõ╩²ź╬®`ź╔Ż║ ?z n ? fn (z n?1 ) ? ? f n?1 ?z n?1 (z n?1 ) (13.47) ę“ūėź╬®`ź╔Ż║ ?f n ?z n (z n ) ? ? f n (z n?1 , z n ) ? z n?1 ? f n (z n?1 ) (13.48) z n?1 ?f n ?z n (z n ) ? ? f n (z n?1 , z n ) ? f n?1 ?z n?1 (z n?1 ) (13.49) z n?1
- 22. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 2. Ė„ź╬®`ź╔żŪźßź├ź╗®`źĖż“ėŗ╦Ń ©C źšź®ź’®`ź╔-źąź├ź»ź’®`ź╔źóźļź┤źĻź║źÓż╚ż╬▒╚▌^ Ęe║═źóźļź┤źĻź║źÓ ?f n ?z n (z n ) ? ? f n (z n ?1 , z n ) ? f n?1 ?z n?1 (z n ?1 ) (13.49) z n?1 (13.46) ? ? p(z n | z n ?1 ) p(x n | z n ) ? f n?1 ?z n?1 (z n ?1 ) z n?1 ? (z n ) ? ? f n ?z n (z n ) źšź®ź’®`ź╔-źąź├ź»ź’®`ź╔źóźļź┤źĻź║źÓ ? (z n ) ? p(x n | z n )? ? (z n?1 ) p(z n | z n ?1 ) (13.36) z n?1
- 23. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 2. Ė„ź╬®`ź╔żŪźßź├ź╗®`źĖż“ėŗ╦Ń ©C źšź®ź’®`ź╔-źąź├ź»ź’®`ź╔źóźļź┤źĻź║źÓż╚ż╬▒╚▌^ ? (z n ) ? ? f n ?z n (z n ) (13.50)
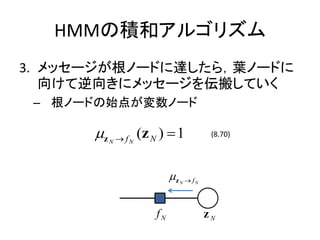
- 24. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 3. źßź├ź╗®`źĖż¼Ė∙ź╬®`ź╔ż╦▀_żĘż┐żķŻ¼╚~ź╬®`ź╔ż╦ Ž“ż▒żŲ─µŽ“żŁż╦źßź├ź╗®`źĖż“ü╗░߿ʿŲżżż» ©C Ė∙ź╬®`ź╔ż╬╩╝ĄŃż¼ēõ╩²ź╬®`ź╔ ?z N ? fN (z N ) ? 1 (8.70) ?z N ? fN fN zN
- 25. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 3. źßź├ź╗®`źĖż¼Ė∙ź╬®`ź╔ż╦▀_żĘż┐żķŻ¼╚~ź╬®`ź╔ż╦ Ž“ż▒żŲ─µŽ“żŁż╦źßź├ź╗®`źĖż“ü╗░߿ʿŲżżż» ©C źšź®ź’®`ź╔-źąź├ź»ź’®`ź╔źóźļź┤źĻź║źÓż╚ż╬▒╚▌^ Ęe║═źóźļź┤źĻź║źÓ ?z N ? fN (z N ) ? 1 (8.70) ? (z N ) ? ? z N ? fN (z N ) źšź®ź’®`ź╔-źąź├ź»ź’®`ź╔źóźļź┤źĻź║źÓ ? (z N ) ? 1 (13.37)
- 26. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 3. źßź├ź╗®`źĖż¼Ė∙ź╬®`ź╔ż╦▀_żĘż┐żķŻ¼╚~ź╬®`ź╔ż╦ Ž“ż▒żŲ─µŽ“żŁż╦źßź├ź╗®`źĖż“ü╗░߿ʿŲżżż» ?z n ? fn (z n ) ? ? f n?1 ?z n (z n ) ? ? f n?1 (z n , z n?1 ) ? z n?1 ? f n?1 (z n?1 ) (13.51)Ī» z n?1 ?z n ? fn ?f n?1 ? z n ?z n?1 ? f n?1 fn zn f n ?1 z n ?1
- 27. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 3. źßź├ź╗®`źĖż¼Ė∙ź╬®`ź╔ż╦▀_żĘż┐żķŻ¼╚~ź╬®`ź╔ż╦ Ž“ż▒żŲ─µŽ“żŁż╦źßź├ź╗®`źĖż“ü╗░߿ʿŲżżż» ©C źšź®ź’®`ź╔-źąź├ź»ź’®`ź╔źóźļź┤źĻź║źÓż╚ż╬▒╚▌^ Ęe║═źóźļź┤źĻź║źÓ ?z n ? fn (z n ) ? ? f n ?1 (z n , z n ?1 ) ? z n?1 ? f n?1 (z n ?1 ) (13.51)Ī» z n?1 (13.46) ? ? p(z n ?1 | z n ) p(x n ?1 | z n ?1 ) ? z n?1 ? f n?1 (z n ?1 ) z n?1 ? (z n ) ? ? z n ? fn (z n ) źšź®ź’®`ź╔-źąź├ź»ź’®`ź╔źóźļź┤źĻź║źÓ ? (z n ) ? ? ? (z n?1 ) p(x n?1 | z n?1 ) p(z n?1 | z n ) (13.38) z n?1
- 28. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 3. źßź├ź╗®`źĖż¼Ė∙ź╬®`ź╔ż╦▀_żĘż┐żķŻ¼╚~ź╬®`ź╔ż╦ Ž“ż▒żŲ─µŽ“żŁż╦źßź├ź╗®`źĖż“ü╗░߿ʿŲżżż» ©C źšź®ź’®`ź╔-źąź├ź»ź’®`ź╔źóźļź┤źĻź║źÓż╚ż╬▒╚▌^ ? (z n ) ? ? z n ? fn (z n ) (13.52)Ī»
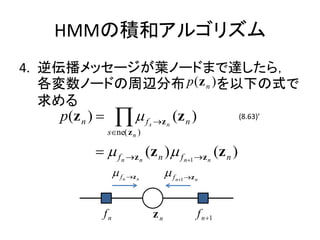
- 29. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 4. ─µü╗▓źźßź├ź╗®`źĖż¼╚~ź╬®`ź╔ż▐żŪ▀_żĘż┐żķŻ¼ Ė„ēõ╩²ź╬®`ź╔ż╬ų▄▐xĘų▓╝ p ( z n ) ż“ęįŽ┬ż╬╩ĮżŪ Ū¾żßżļ p ( z n ) ? ? ? f s ?z n ( z n ) (8.63)Ī» s?ne( z n ) ? ? f n ?z n (z n ) ? f n?1 ?z n (z n ) ?f n ?z n ?f n?1 ? z n fn zn f n ?1
- 30. HMMż╬Ęe║═źóźļź┤źĻź║źÓ ų▄▐xĘų▓╝ p ( z n ) żŽ╝╚ż╦ėQ£yēõ╩² X ? ?x1 , ? , x N ? ż╦żĶżĻ╠§╝■ĖČż▒żķżņżŲżżżļż╬żŪŻ¼ p(z n , X) ? ? f n ?z n (z n )?z n ? f n (z n ) ? ? (z n )? (z n ) (13.53) p(z n , X) ? (z n )? (z n ) ? (z n ) ? ? (13.54) p(X) p( X) (13.33)ż╚═¼żĖ”├ (zn)ż¼ī¦ż▒ż┐ŻĪ
- 31. HMMż╬Ęe║═źóźļź┤źĻź║źÓ 5. Ė„ę“ūėź╬®`ź╔ż╦ĮėŠAżĄżņż┐ų▄▐xż╬ēõ╩²╚║ x s ż╬═¼ĢrĘų▓╝żŽęįŽ┬ż╬╩ĮżŪŪ¾żßżļ p(x s ) ? f s (x s ) ?? i?ne( f s ) xi ? f s ( xi ) (8.72) p(z n?1 , z n ) ? f n (z n?1 , z n )?z n ? f n (z n )?z n?1 ? f n (z n?1 ) ?z n?1 ? f n ?z n ? fn z n ?1 fn zn
- 32. HMMż╬Ęe║═źóźļź┤źĻź║źÓ č▌┴Ģ13.11 ”╬ (zn-1, zn)ż“ī¦ż» p(z n?1 , z n , X) ? f n (z n?1 , z n ) ?z n ? f n (z n ) ?z n?1 ? f n (z n?1 ) ? p(z n | z n?1 ) p(x n | z n ) ? (z n )? (z n?1 ) p(z n ?1 , z n , X) ? (z n ?1 , z n ) ? p(z n ?1 , z n | X) ? p ( X) ? (z n ?1 ) p(x n | z n ) p(z n | z n ?1 ) ? (z n ) ? p ( X) (13.43)ż╚═¼żĖ”╬ (zn-1, zn)ż¼ī¦ż▒ż┐ŻĪ
- 33. ż▐ż╚żß ? Ęe║═źóźļź┤źĻź║źÓżŪżŌźšź®ź’®`ź╔-źąź├ź»ź’®`ź╔ źóźļź┤źĻź║źÓż╚═¼żĖż│ż╚ż¼żŪżŁż┐ĪŻ