NLPforml5
- 1. 自然言语のための机械学习勉强会 第5章:系列ラベリング @kisa12012
- 2. 目次 ? 5.1:系列ラベリング概論 ? 5.2:隠れマルコフモデル(HMM) ? 5.3:系列ラベリングの逐次的手法 ? 5.4:条件付確率場(CRF) ? 5.5:まとめ
- 3. 目次 ? 5.1:系列ラベリング概論 ? 5.2:隠れマルコフモデル(HMM) ? 5.3:系列ラベリングの逐次的手法 ? 5.4:条件付確率場(CRF) ? 5.5:まとめ
- 4. 5.1 系列ラベリング概論 ? 系列ラベリング ? 品詞タグ付け ? チャンキング(文書内から人名?地名の抽出) ? 品詞タグ付け “Nurture passes nature.” 名詞 動詞 名詞 ? 系列(sequence) ”Nurture passes nature.” いくつかの要素が連なったもの ? 系列ラベリング(sequential labeling) 『Nurture←名詞』を付与 系列内のそれぞれにラベルを付けること
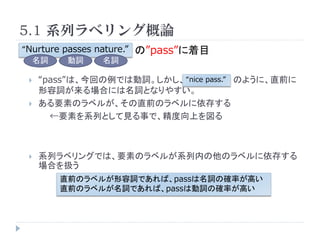
- 5. 5.1 系列ラベリング概論 “Nurture passes nature.” の”pass”に着目 名詞 動詞 名詞 ? “pass”は、今回の例では動詞。しかし、 “nice pass.” のように、直前に 形容詞が来る場合には名詞となりやすい。 ? ある要素のラベルが、その直前のラベルに依存する ←要素を系列として見る事で、精度向上を図る ? 系列ラベリングでは、要素のラベルが系列内の他のラベルに依存する 場合を扱う 直前のラベルが形容詞であれば、passは名詞の確率が高い 直前のラベルが名詞であれば、passは動詞の確率が高い
- 6. 5.1 系列ラベリング概論 ? チャンキング(chunking) [5.5章] ? 言語表現の意味的あるいは文法的にまとまった部分を発見する研究 ? 名詞句の抽出や人名抽出などが挙げられる “After stubbing out the cigarette, Lunvalet talked to me.” 人名 “Lunvalet”という人名が存在することを知らなくても、文脈から推測する ことが出来る ? 複数語からなる表現が人を指していることもある “Suddenly, the tall German guy talked to me.” O B I I I O O O 人 B(人名開始単語),I(人名部),O(その他)のようにタグ付けがしたい
- 7. 5.1 系列ラベリング概論 B,I,Oのように抽出のための用いられるラベルをIOB2タグという IOB2タグ付けも系列ラベリングの一種 ? 系列ラベリングの問題点 ? 可能なラベル列の組み合わせ数が膨大 ? [組み合わせ数] = [品詞種類数]の[要素数]乗 ? 可能な品詞列を全て列挙して分類器を作成することは不可能 ? 系列ラベリングには、特別な手法が必要となる ? 文書は文?単語の系列と見ることが出来るため、系列ラベリングは言語 処理において非常に有用
- 8. 目次 ? 5.1:系列ラベリング概論 ? 5.2:隠れマルコフモデル(HMM) ? 5.3:系列ラベリングの逐次的手法 ? 5.4:条件付確率場(CRF) ? 5.5:まとめ
- 9. 5.2 隠れマルコフモデル(HMM) ? 隠れマルコフモデル(Hidden Markov Model) ? 系列ラベリングに用いることが出来る非常にシンプルなモデル ? 通常は、ラベルの付いていない系列データのみが与えられたときにパ ラメータを推定する手法の事を指す。しかし、ここでは系列ラベリングの ためのラベル付き訓練データが与えられている状態を想定している 要 要 要 要 要 要 素 素 素 素 素 素 ラ ラ ラ ラ ラ ラ ベ ベ ベ ベ ベ ベ ル ル ル ル ル ル
- 10. 5.2.1 HMMの導入 ? 数式表記の定義 x = ( x1 , x2 ,..., xk ) : 系列 y = ( y1 , y2 ,..., yk ) :ラベル列 ? 仮定 ? 各状態は、その直前の状態のみに依存すると仮定 ? つまり、(xi,yi)は、(xi-1,yi-1)にのみ依存すると仮定 ? より詳細には、 xiはyiにのみ、 yiはyi-1にのみ依存すると仮定
- 11. 5.2.1 HMMの導入 xとyの同時確率は、以下の式で導出できる P (x, y ) = P ( xk , yk | xk ?1 , yk ?1 ) P( xk ?1 , yk ?1 | xk ? 2 , yk ? 2 )...P ( x1 , y1 | x0 , y0 ) = ∏ P ( xi , yi | xi ?1 , yi ?1 ) i = ∏ P( xi | yi ) P( yi | yi ?1 ) i 簡単のため、ダミー要素(x0,y0)を用意し、以下の式を用いた P( x1 , y1 ) = P( x1 , y1 | x0 , y0 ) P( y1 ) = P( y1 | y0 )
- 12. 5.2.2 パラメータ推定 訓練データ: D = {( x (1) , y (1) ),..., (x , y (D) (D) )} の最尤推定解を求めることで、パラ メータP( x | y ), P( y | y ' ) を推定する まず、対数尤度 log P( D) を下式のように表す log P ( D ) = ∑ log P(x (i ) , y (i ) ) ( x ( i ) , y ( i ) )∈D ? ? = ∑ ? ∑ log P ( x j | y j ) + ∑ log P ( y j | y j ?1 ) ? ? (i ) (i ) (i ) (i ) ? ( x ( i ) , y ( i ) )∈D ? j j ? = ∑ n(( x, y ), D) log P( x | y ) + ∑ n(( y ' , y ), D) log P( y | y ' ) x, y y, y' = ∑ [データDで、xにラベルyが付与された回数] log p x| y x, y + ∑ [データDで、ラベルy'の次にラベルyが出現した回数] log q y '| y y ', y
- 13. 5.2.2 パラメータ推定 制約条件を考慮すると、最尤推定解は以下の問題を解くことで導出できる max ∑ n(( x, y ), D) log p x| y + ∑ n(( y ' , y ), D) log q y| y ' x, y y, y' s.t. ∑p x x| y =1 ∑p y y| y ' =1 ラグランジュ法を用いて、最大化するパラメータを求めると、以下の式になる (演習問題1) n(( x, y ), D) p x| y = ∑ n(( x, y), D) x n(( y ' , y ), D) q y| y ' = ∑ n(( y' , y), D) x 要素とラベル、ラベルとラベルの組み合わせの出現頻度を パラメータとしているだけなので、当たり前の結果
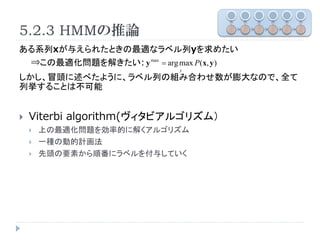
- 14. 5.2.3 HMMの推論 ある系列xが与えられたときの最適なラベル列yを求めたい ?この最適化問題を解きたい: y max = arg max P(x, y ) y しかし、冒頭に述べたように、ラベル列の組み合わせ数が膨大なので、全て 列挙することは不可能 ? Viterbi algorithm(ヴィタビアルゴリズム) ? 上の最適化問題を効率的に解くアルゴリズム ? 一種の動的計画法 ? 先頭の要素から順番にラベルを付与していく
- 15. Viterbi algorithm Pseudocode(前半) 入力:系列x for j=2 to |x| for all yj t ( j , y j ) = max[log P( x j , y j | x j ?1 , y j ?1 ) + t ( j ? 1, y j ?1 )] y j ?1 s ( j , y j ) = arg max[log P( x j , y j | x j ?1 , y j ?1 ) + t ( j ? 1, y j ?1 )] y j ?1 end for 全ての要素に対応する全てのラベルについて、どのラベル end for から遷移する確率が高いかを比較する t(j,yj):要素jに対応するラベルがyjをとる条件のもと、確率が最大となるラ ベル列をとる確率。 s(j,yj):確率が最大となるラベルをとった場合のyj-1を保存。アルゴリズムの 後半で使用。
- 16. Viterbi algorithm Pseudocode(後半) 前半部のイメージ 最適なラベル列を探す 後半部 入力:t(|x|,y),s y|max = arg max t (| x |, y ) x| y for j=|x|-1 to 1 y max = s ( j + 1, y max ) j j +1 end for 最適なラベル列を後ろ側の要素から順に、逆向きに取り出している
- 17. 目次 ? 5.1:系列ラベリング概論 ? 5.2:隠れマルコフモデル(HMM) ? 5.3:系列ラベリングの逐次的手法 ? 5.4:条件付確率場(CRF) ? 5.5:まとめ
- 18. 5.3 通常の分類器の逐次適用 ? 4章の分類器を逐次的に用いることで、系列ラベリングを行う 方法もある ? Ex. P ( y j | x j ?1 , x j , x j +1 y j ?1 ) 分類器はなんでもよい(Na?ve Bayes/SVMなど) ? 分類器の逐次適用の特徴 ? 直後の要素を用いる事もできる ? 各要素について、様々な素性を用いることが出来る ? 一般的に、計算時間が増大する ? ラベル系列全体の確からしさは考慮していない
- 19. 目次 ? 5.1:系列ラベリング概論 ? 5.2:隠れマルコフモデル(HMM) ? 5.3:系列ラベリングの逐次的手法 ? 5.4:条件付確率場(CRF) ? 5.5:まとめ
- 20. 5.4 条件付確率場(CRF) ? 条件付確率場(Conditional Random Field) ? CRFと呼ばれることが多い ? 様々な素性を用いることが出来、またラベル系列全体の確からしさにも 焦点を当てた学習を行えるモデル ? 4.5節の対数線形モデルを系列ラベリング問題へ適用したもの 訓練データ: D = {( x (1) , y (1) ),..., (x (D) (D) ,y )} が与えられたとする この時、ラベル列の系列に対する条件付き確率を以下のようにおく 1 P ( y | x) = exp(w ? Φ(x, y)) Z x,w w : 素性に対する重みベクトル ? ? Z x,w : 正規化係数? Z x, w = ? ∑ exp(w ? Φ(x, y)) ? ? ? y ?
- 21. 5.4.1 条件付確率場(CRF)の導入 最適なラベル列を求めたい。よって、以下の最大化問題を解く 1 y ? = arg max exp(w ? Φ(x, y)) y Z x,w = arg max w ? Φ(x, y) y ただし、この最大化問題を解くのは非常に時間がかかるため、yは隣り合う ラベルyt,yt-1にのみに依存するという条件をおく φk (x, y ) = ∑ φk (x, yt , yt ?1 ) t w ? Φ(x, y) = w ? ∑ φk (x, yt , yt ?1 ) t = ∑ w ? φk (x, yt , yt ?1 ) t y ? = arg max ∑ w ? φk (x, yt , yt ?1 ) y t
- 22. 5.4.1 条件付確率場(CRF)の導入 y ? = arg max ∑ w ? φk (x, yt , yt ?1 ) y t 上式ならば、wが分かっていればViterbi Algorithmで高速に解くことがで きる t ( j , y j ) = max[log P( x j , y j | x j ?1 , y j ?1 ) + t ( j ? 1, y j ?1 )] y j ?1 s ( j , y j ) = arg max[log P( x j , y j | x j ?1 , y j ?1 ) + t ( j ? 1, y j ?1 )] y j ?1 t ( j , y j ) = max[w ? Φ(x, y j , y j ?1 ) + t ( j ? 1, y j ?1 )] y j ?1 s ( j , y j ) = arg max[w ? Φ(x, y j , y j ?1 ) + t ( j ? 1, y j ?1 )] y j ?1 モデルの拡張も容易に可能 φk (x, y ) = ∑ φk (x, yt , yt ?1 , yt ? 2 ) t
- 23. 5.4.2 条件付確率場(CRF)の学習 Wの学習方法 以下の目的関数を最大化する L(w ) = ∑ log P(y | x) = ∑ w ? Φ(x, y) ? log Z D D x,w 実際は、正則化項を加えた目的 関数を最適化する場合が多い L(w ) ? C | w | 2 しかし、上式は解析的に解くことが不可能 最急勾配法(1.2.2節)を用いる(準ニュートン法や確率的勾配法が用いられやすい) w new = w old + ε? w L(w old ) ? ? ? w L(w old )= ∑ ? Φ ( x (i ) , y (i ) ) ? ? ∑ P ( y | x )Φ ( x , y ) ? (i ) (i ) ? D ? y ? 系列ラベリングではyの組み合わせが膨大で、 P(y|x)が計算不可能
- 24. 5.4.2 条件付確率場(CRF)の学習 ∑ P ( y | x )Φ ( x , y ) = ∑ P ( y | x )∑ Φ ( x , y , y ) y (i ) (i ) y (i ) t (i ) t t ?1 = ∑ ∑ P( y , y t yt , yt ?1 t t ?1 | x (i ) )Φ (x (i ) , yt , yt ?1 ) と変形することで、P( yt , yt ?1 | x (i ) ) が計算できればよい形となる ? t ( yt , yt ?1 ) = exp( w ? Φ (x, yt , yt ?1 ))とおけば、 ? t ( yt , yt ?1 ) P ( y | x) = ∏ t Z x,w と書けるので、 P( yt , yt ?1 | x) = ∑ ∑ P ( y | x) y 0:t ?2 y t +1:T +1 ∑ ∑ ∏? ( y , y 1 = t' t' t '?1 ) Z x, w y 0:t ?2 y t +1:T +1 t' ? t ( yt , yt ?1 ) = Z x, w ∑ ∑ ∏? ( y , y y 0:t ?2 y t +1:T +1 t '≠ t t' t' t '?1 )
- 25. 5.4.2 条件付確率場(CRF)の学習 ∑ ∑ ∏? ( y , y ) y 0:t ?2 y t +1:T +1 t '≠ t t' t' t '?1 ? t ?1 ?? T +1 ? ? t ? = ? ? ∑∏ ? t ' ( yt ' , yt '?1 ) ?? ?? ∑∏ ? t ' ( yt ' , yt '?1 ) ? ? α ( yt , t ) = ? ? ∑∏ ? t ' ( yt ' , yt '?1 ) ? ? ? y 0:t ?2 t '=1 ?? y t +1:T +1 t '=t +1 ? ? y 0:t ?2 t '=1 ? = α ( yt ?1 , t ? 1) β ( yt , t ) ? T +1 ? 1 β ( yt , t ) = ? ? ∑∏ ? t ' ( yt ' , yt '?1 ) ? ? P( yt , yt ?1 | x) = ? t ( yt , yt ?1 )α ( yt ?1 , t ? 1) β ( yt , t ) ? y t +1:T +1 t '=t +1 ? Z x,w 上式が高速に計算できればよい α ( yt , t ) = ∑? ( y , y t t t ?1 )α ( yt ?1 , t ? 1) α β yt ?1 β ( yt , t ) = ∑? yt +1 t +1 ( yt +1 , yt ) β ( yt +1 , t + 1) Z x,w = ∑α ( y yT T ,T ) を利用すれば、DPを用いて高速に計算可能になる
- 26. 5.4.2 条件付確率場(CRF)の学習 α ( yt , t ), β ( yt , t ) を利用したこのような算法は、前向き?後ろ向きアルゴリズム (forward-backward algorithm)の一種 一般のCRFは、系列上のノードだけでなく、グラフ上のノードのラベリング問 題に適用可能(Ex.係り受け解析)
- 27. 目次 ? 5.1:系列ラベリング概論 ? 5.2:隠れマルコフモデル(HMM) ? 5.3:系列ラベリングの逐次的手法 ? 5.4:条件付確率場(CRF) ? 5.5:まとめ
- 28. 5.5 まとめ ? 系列ラベリング ? 隠れマルコフモデル(HMM) ? 分類器の逐次適用 ? 条件付確率場(CRF) の3種について、説明をした ? 系列ラベリング全体としては、NLP2006チュートリアルも参照するとよ い http://www.geocities.co.jp/Technopolis/5893/publication/N LP2006slide.pdf ? HMMのforward-backward algorithm : Baum- Welch algorithm ? これは、EM algorithmの一種(3.5節)
- 29. 5.5 まとめ ? 分類器による逐次適用による系列ラベリングで特筆すべきもの ? YamChaにも用いられているSVMを用いた系列ラベリング ? CRFを自然言語処理に応用したものとして、MALLET,CRF++など ? 木構造に対してCRFを扱うには、確率伝播法(belief propagation)が 必要 (Bishop本:8.4節) ? チャンキングにはIOB2タグ以外にも、様々な変種が存在



![5.1 系列ラベリング概論
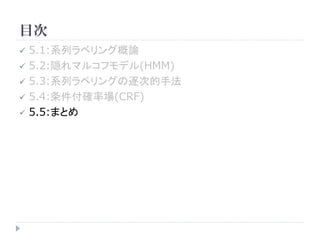
? チャンキング(chunking) [5.5章]
? 言語表現の意味的あるいは文法的にまとまった部分を発見する研究
? 名詞句の抽出や人名抽出などが挙げられる
“After stubbing out the cigarette, Lunvalet talked to me.”
人名
“Lunvalet”という人名が存在することを知らなくても、文脈から推測する
ことが出来る
? 複数語からなる表現が人を指していることもある
“Suddenly, the tall German guy talked to me.”
O B I I I O O O
人
B(人名開始単語),I(人名部),O(その他)のようにタグ付けがしたい](https://image.slidesharecdn.com/nlpforml5-100807023449-phpapp02/85/NLPforml5-6-320.jpg)
![5.1 系列ラベリング概論
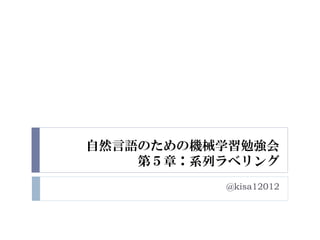
B,I,Oのように抽出のための用いられるラベルをIOB2タグという
IOB2タグ付けも系列ラベリングの一種
? 系列ラベリングの問題点
? 可能なラベル列の組み合わせ数が膨大
? [組み合わせ数] = [品詞種類数]の[要素数]乗
? 可能な品詞列を全て列挙して分類器を作成することは不可能
? 系列ラベリングには、特別な手法が必要となる
? 文書は文?単語の系列と見ることが出来るため、系列ラベリングは言語
処理において非常に有用](https://image.slidesharecdn.com/nlpforml5-100807023449-phpapp02/85/NLPforml5-7-320.jpg)


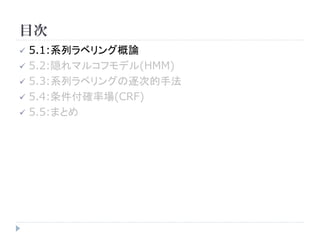
![5.2.2 パラメータ推定
訓練データ: D = {( x (1) , y (1) ),..., (x , y
(D) (D)
)} の最尤推定解を求めることで、パラ
メータP( x | y ), P( y | y ' ) を推定する
まず、対数尤度 log P( D) を下式のように表す
log P ( D ) = ∑ log P(x (i )
, y (i ) )
( x ( i ) , y ( i ) )∈D
? ?
= ∑ ? ∑ log P ( x j | y j ) + ∑ log P ( y j | y j ?1 ) ?
?
(i ) (i ) (i ) (i )
?
( x ( i ) , y ( i ) )∈D ? j j ?
= ∑ n(( x, y ), D) log P( x | y ) + ∑ n(( y ' , y ), D) log P( y | y ' )
x, y y, y'
= ∑ [データDで、xにラベルyが付与された回数] log p x| y
x, y
+ ∑ [データDで、ラベルy'の次にラベルyが出現した回数] log q y '| y
y ', y](https://image.slidesharecdn.com/nlpforml5-100807023449-phpapp02/85/NLPforml5-12-320.jpg)

![Viterbi algorithm Pseudocode(前半)
入力:系列x
for j=2 to |x|
for all yj
t ( j , y j ) = max[log P( x j , y j | x j ?1 , y j ?1 ) + t ( j ? 1, y j ?1 )]
y j ?1
s ( j , y j ) = arg max[log P( x j , y j | x j ?1 , y j ?1 ) + t ( j ? 1, y j ?1 )]
y j ?1
end for
全ての要素に対応する全てのラベルについて、どのラベル
end for から遷移する確率が高いかを比較する
t(j,yj):要素jに対応するラベルがyjをとる条件のもと、確率が最大となるラ
ベル列をとる確率。
s(j,yj):確率が最大となるラベルをとった場合のyj-1を保存。アルゴリズムの
後半で使用。](https://image.slidesharecdn.com/nlpforml5-100807023449-phpapp02/85/NLPforml5-15-320.jpg)




![5.4.1 条件付確率場(CRF)の導入
y ? = arg max ∑ w ? φk (x, yt , yt ?1 )
y t
上式ならば、wが分かっていればViterbi Algorithmで高速に解くことがで
きる
t ( j , y j ) = max[log P( x j , y j | x j ?1 , y j ?1 ) + t ( j ? 1, y j ?1 )]
y j ?1
s ( j , y j ) = arg max[log P( x j , y j | x j ?1 , y j ?1 ) + t ( j ? 1, y j ?1 )]
y j ?1
t ( j , y j ) = max[w ? Φ(x, y j , y j ?1 ) + t ( j ? 1, y j ?1 )]
y j ?1
s ( j , y j ) = arg max[w ? Φ(x, y j , y j ?1 ) + t ( j ? 1, y j ?1 )]
y j ?1
モデルの拡張も容易に可能
φk (x, y ) = ∑ φk (x, yt , yt ?1 , yt ? 2 )
t](https://image.slidesharecdn.com/nlpforml5-100807023449-phpapp02/85/NLPforml5-22-320.jpg)