H05 Parallhles
- 1. О ОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ О–ОҝП…ПҒОҪО¬ ОҶОҪОҪОұПӮ
- 2. ОЈПҮОөП„О№ОәО® ОёОӯПғО· ПғО·ОјОөОҜПүОҪ ПүПӮ ПҖПҒОҝПӮ ОөП…ОёОөОҜОұ О— ОөП…ОёОөОҜОұ (Оө) ПҮПүПҒОҜО¶ОөО№ П„Оҝ ОөПҖОҜПҖОөОҙОҝ ПғОө ОҙПҚОҝ О·ОјО№ОөПҖОҜПҖОөОҙОұ. (Оө)
- 3. ОЈПҮОөП„О№ОәО® ОёОӯПғО· ПғО·ОјОөОҜПүОҪ ПүПӮ ПҖПҒОҝПӮ ОөП…ОёОөОҜОұ О•ОҜОҪОұО№ Оҝ ОЈОҪОҝПҚПҖП… ОәОұО№ Оҝ ОӨПғО¬ПҒО»П… ОңПҖПҒО¬ОҝП…ОҪ ОұПҖПҢ П„О·ОҪ ОҜОҙО№Оұ ОјОөПҒО№О¬ П„О·ПӮ (Оө); (Оө)
- 4. ОЈПҮОөП„О№ОәО® ОёОӯПғО· ПғО·ОјОөОҜПүОҪ ПүПӮ ПҖПҒОҝПӮ ОөП…ОёОөОҜОұ ОҢПҮО№ ОөОҜОҪОұО№ ОөОҪОұО»О»О¬Оҫ П„О·ПӮ (Оө) (Оө)
- 5. ОЈПҮОөП„О№ОәО® ОёОӯПғО· ПғО·ОјОөОҜПүОҪ ПүПӮ ПҖПҒОҝПӮ ОөП…ОёОөОҜОұ (Оө) О•ОҜОҪОұО№ Оҝ ОЈОҪОҝПҚПҖП… ОәОұО№ Оҝ О“ОҝПҚОҪП„ПғП„ОҝОә ОұПҖПҢ П„О·ОҪ ОҜОҙО№Оұ ОјОөПҒО№О¬ П„О·ПӮ (Оө);
- 6. ОЈПҮОөП„О№ОәО® ОёОӯПғО· ПғО·ОјОөОҜПүОҪ ПүПӮ ПҖПҒОҝПӮ ОөП…ОёОөОҜОұ ОқОұО№, ОөОҜОҪОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө). (Оө)
- 7. О“О№Оұ ОҪОұ ОҙОҝПҚОјОө П„ПҺПҒОұ ОұОҪ ОәОұП„ОұО»О¬ОІОұОјОө ПғПүПғП„О¬вҖҰ ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
- 8. Оҹ ОӨПғО¬ПҒО»П… ОңПҖПҒО¬ОҝП…ОҪ ОәОұО№ Оҝ О“ОҝПҚОҪП„ПғП„ОҝОә ОөОҜОҪОұО№ ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
- 9. Оҹ ОӨПғО¬ПҒО»П… ОңПҖПҒО¬ОҝП…ОҪ ОәОұО№ Оҝ О“ОҝПҚОҪП„ПғП„ОҝОә ОөОҜОҪОұО№ ОөОҪОұО»О»О¬Оҫ П„О·ПӮ (Оө). ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
- 10. О— ОӣОҝПҚПғП… ОәОұО№ Оҝ ОЈОҪОҝПҚПҖП… ОөОҜОҪОұО№ ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
- 11. О— ОӣОҝПҚПғП… ОәОұО№ Оҝ ОЈОҪОҝПҚПҖП… ОөОҜОҪОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө). ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
- 12. Оҹ ОӣОҜОҪОҝП…ПӮ ОәОұО№ Оҝ ОЈПҒОӯОҪП„ОөПҒ ОөОҜОҪОұО№ ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
- 13. Оҹ ОӣОҜОҪОҝП…ПӮ ОәОұО№ Оҝ ОЈПҒОӯОҪП„ОөПҒ ОөОҜОҪОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө). ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
- 14. Оҹ О“ОҝПҚОҪП„ПғП„ОҝОә ОәОұО№ Оҝ ОЈОҪОҝПҚПҖП… ОөОҜОҪОұО№ ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
- 15. Оҹ О“ОҝПҚОҪП„ПғП„ОҝОә ОәОұО№ Оҝ ОЈОҪОҝПҚПҖП… ОөОҜОҪОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө). ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
- 16. Оҹ ОӨПғО¬ПҒО»П… ОңПҖПҒО¬ОҝП…ОҪ ОәОұО№ О· ОӣОҝПҚПғП… ОөОҜОҪОұО№ ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
- 17. Оҹ ОӨПғО¬ПҒО»П… ОңПҖПҒО¬ОҝП…ОҪ ОәОұО№ О· ОӣОҝПҚПғП… ОөОҜОҪОұО№ ОөОҪОұО»О»О¬Оҫ П„О·ПӮ (Оө). ОЈПҒОӯОҪП„ОөПҒ (Оө) ОӣОҜОҪОҝП…ПӮ ОӣОҝПҚПғП…
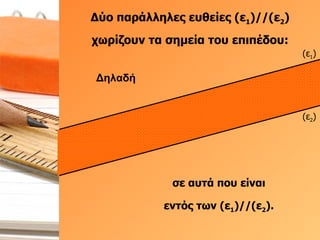
- 18. О”ПҚОҝ ПҖОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ (Оө 1 )//(Оө 2 ) ПҮПүПҒОҜО¶ОҝП…ОҪ П„Оұ ПғО·ОјОөОҜОұ П„ОҝП… ОөПҖО№ПҖОӯОҙОҝП…: ПғОө ОұП…П„О¬ ПҖОҝП… ОөОҜОҪОұО№ ОұОҪО¬ОјОөПғОұ ПғП„О№ПӮ ОҙПҚОҝ ОөП…ОёОөОҜОөПӮ. (Оө 1 ) (Оө 2 )
- 19. О”ПҚОҝ ПҖОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ (Оө 1 )//(Оө 2 ) ПҮПүПҒОҜО¶ОҝП…ОҪ П„Оұ ПғО·ОјОөОҜОұ П„ОҝП… ОөПҖО№ПҖОӯОҙОҝП…: ПғОө ОұП…П„О¬ ПҖОҝП… ОөОҜОҪОұО№ ОөОҪП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ). (Оө 1 ) (Оө 2 ) О”О·О»ОұОҙО®
- 20. ОәОұО№ ПғОө ОұП…П„О¬ ПҖОҝП… ОҙОөОҪ ОөОҜОҪОұО№ ОұОҪО¬ОјОөПғОұ ПғП„О№ПӮ ОҙПҚОҝ ОөП…ОёОөОҜОөПӮ. О”ПҚОҝ ПҖОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ (Оө 1 )//(Оө 2 ) ПҮПүПҒОҜО¶ОҝП…ОҪ П„Оұ ПғО·ОјОөОҜОұ П„ОҝП… ОөПҖО№ПҖОӯОҙОҝП…: (Оө 1 ) (Оө 2 )
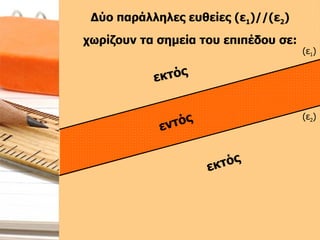
- 21. О”ПҚОҝ ПҖОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ (Оө 1 )//(Оө 2 ) ПҮПүПҒОҜО¶ОҝП…ОҪ П„Оұ ПғО·ОјОөОҜОұ П„ОҝП… ОөПҖО№ПҖОӯОҙОҝП… ПғОө: (Оө 1 ) (Оө 2 ) ПғОө ОұП…П„О¬ ПҖОҝП… ОөОҜОҪОұО№ ОөОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ). О”О·О»ОұОҙО®
- 22. О”ПҚОҝ ПҖОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ (Оө 1 )//(Оө 2 ) ПҮПүПҒОҜО¶ОҝП…ОҪ П„Оұ ПғО·ОјОөОҜОұ П„ОҝП… ОөПҖО№ПҖОӯОҙОҝП… ПғОө: (Оө 1 ) (Оө 2 ) ОөОҪП„ПҢПӮ ОөОәП„ПҢПӮ ОөОәП„ПҢПӮ
- 23. О”ПҚОҝ ПҖОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ (Оө 1 )//(Оө 2 ) (Оө 1 ) (Оө 2 ) О•ОҪП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОөОҜОҪОұО№ ОҝО№: О“ОҝПҚОҪП„ПғП„ОҝОә ОәОұО№ ОӣОҜОҪОҝП…ПӮ
- 24. О”ПҚОҝ ПҖОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ (Оө 1 )//(Оө 2 ) (Оө 1 ) (Оө 2 ) О•ОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОөОҜОҪОұО№ ОҝО№: ОЈОҪОҝПҚПҖП…, ОЈПҒОӯОҪП„ОөПҒ, ОӣОҝПҚПғП… ОәОұО№ ОӨПғО¬ПҒО»П… ОңПҖПҒО¬ОҝП…ОҪ
- 25. О ОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ ПҖОҝП… П„ОӯОјОҪОҝОҪП„ОұО№ ОұПҖПҢ ОјОҜОұ О¬О»О»О· ОөП…ОёОөОҜОұ ОҢП„ОұОҪ ОҙПҚОҝ ПҖОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ П„ОӯОјОҪОҝОҪП„ОұО№ ОұПҖПҢ ОјОҜОұ П„ПҒОҜП„О· ОөП…ОёОөОҜОұ П„ПҢП„Оө ПғПҮО·ОјОұП„ОҜО¶ОҝОҪП„ОұО№ ОҝОәП„ПҺ ОіПүОҪОҜОөПӮ. (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 О’ 1 2 3 4
- 26. О ОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ ПҖОҝП… П„ОӯОјОҪОҝОҪП„ОұО№ ОұПҖПҢ ОјОҜОұ О¬О»О»О· ОөП…ОёОөОҜОұ ОҹО№ ОіПүОҪОҜОөПӮ ПҖОҝП… ОІПҒОҜПғОәОҝОҪП„ОұО№ ОұОҪО¬ОјОөПғОұ ОұПҖПҢ П„О№ПӮ ОөП…ОёОөОҜОөПӮ ОҝОҪОҝОјО¬О¶ОҝОҪП„ОұО№ ОөОҪП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 3 4 О’ 1 2
- 27. О ОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ ПҖОҝП… П„ОӯОјОҪОҝОҪП„ОұО№ ОұПҖПҢ ОјОҜОұ О¬О»О»О· ОөП…ОёОөОҜОұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 О’ 3 4 ОҹО№ ОіПүОҪОҜОөПӮ ПҖОҝП… ОҙОөОҪ ОІПҒОҜПғОәОҝОҪП„ОұО№ ОјОөП„ОұОҫПҚ П„ПүОҪ ОөП…ОёОөО№ПҺОҪ ОҝОҪОҝОјО¬О¶ОҝОҪП„ОұО№ ОөОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 )
- 28. О ОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ ПҖОҝП… П„ОӯОјОҪОҝОҪП„ОұО№ ОұПҖПҢ ОјОҜОұ О¬О»О»О· ОөП…ОёОөОҜОұ ОңПҖОҝПҒОҝПҚОјОө ОҪОұ ОІПҒОҝПҚОјОө О¶ОөПҚОіО· ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ ОіПүОҪО№ПҺОҪ ПғП„Оҝ ПғПҮО®ОјОұ; (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 О’ 1 2 3 4
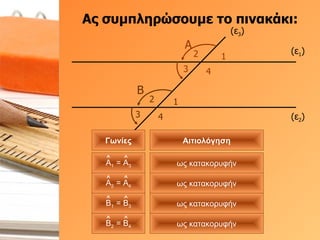
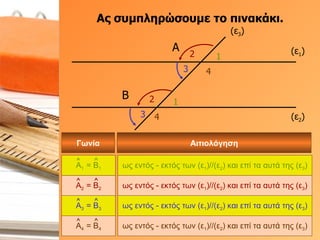
- 29. О‘ПӮ ПғП…ОјПҖО»О·ПҒПҺПғОҝП…ОјОө П„Оҝ ПҖО№ОҪОұОәО¬ОәО№: (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 О’ 1 2 3 4 О“ПүОҪОҜОөПӮ О‘О№П„О№ОҝО»ПҢОіО·ПғО· ПүПӮ ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ ПүПӮ ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ ПүПӮ ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ ПүПӮ ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ О‘ 1 = О‘ 3 О‘ 2 = О‘ 4 О’ 1 = О’ 3 О’ 2 = О’ 4
- 30. О ОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ ПҖОҝП… П„ОӯОјОҪОҝОҪП„ОұО№ ОұПҖПҢ ОјОҜОұ О¬О»О»О· ОөП…ОёОөОҜОұ ОңПҖОҝПҒОҝПҚОјОө ОҪОұ ОІПҒОҝПҚОјОө ПғП„Оҝ ПғПҮО®ОјОұ П„Оұ О¶ОөПҚОіО· П„ПүОҪ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәПҺОҪ ОіПүОҪО№ПҺОҪ ПҖОҝП… ОӯПҮОҝП…ОҪ ОәОҝПҒП…ПҶО® П„Оҝ ПғО·ОјОөОҜОҝ О‘; (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 О’ 1 2 3 4
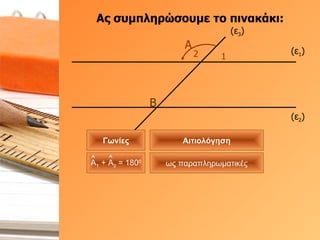
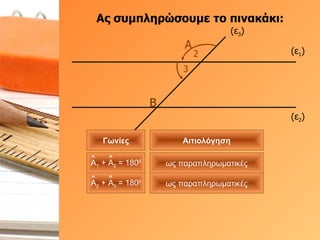
- 31. О‘ПӮ ПғП…ОјПҖО»О·ПҒПҺПғОҝП…ОјОө П„Оҝ ПҖО№ОҪОұОәО¬ОәО№: (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 О’ О“ПүОҪОҜОөПӮ О‘О№П„О№ОҝО»ПҢОіО·ПғО· ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ О‘ 1 + О‘ 2 = 180 0
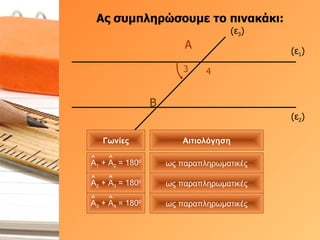
- 32. О‘ПӮ ПғП…ОјПҖО»О·ПҒПҺПғОҝП…ОјОө П„Оҝ ПҖО№ОҪОұОәО¬ОәО№: (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 2 3 О’ О“ПүОҪОҜОөПӮ О‘О№П„О№ОҝО»ПҢОіО·ПғО· ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ О‘ 1 + О‘ 2 = 180 0 О‘ 2 + О‘ 3 = 180 0
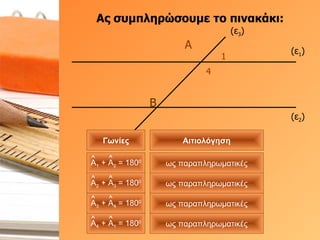
- 33. О‘ПӮ ПғП…ОјПҖО»О·ПҒПҺПғОҝП…ОјОө П„Оҝ ПҖО№ОҪОұОәО¬ОәО№: (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 3 4 О’ О“ПүОҪОҜОөПӮ О‘О№П„О№ОҝО»ПҢОіО·ПғО· ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ О‘ 1 + О‘ 2 = 180 0 О‘ 2 + О‘ 3 = 180 0 О‘ 3 + О‘ 4 = 180 0
- 34. О‘ПӮ ПғП…ОјПҖО»О·ПҒПҺПғОҝП…ОјОө П„Оҝ ПҖО№ОҪОұОәО¬ОәО№: (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 4 О’ О“ПүОҪОҜОөПӮ О‘О№П„О№ОҝО»ПҢОіО·ПғО· ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ О‘ 1 + О‘ 2 = 180 0 О‘ 2 + О‘ 3 = 180 0 О‘ 3 + О‘ 4 = 180 0 О‘ 4 + О‘ 1 = 180 0
- 35. О ОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ ПҖОҝП… П„ОӯОјОҪОҝОҪП„ОұО№ ОұПҖПҢ ОјОҜОұ О¬О»О»О· ОөП…ОёОөОҜОұ ОҹО№ ОөОҪП„ПҢПӮ ОөОҪОұО»О»О¬Оҫ ОіПүОҪОҜОөПӮ ОөОҜОҪОұО№ ОҜПғОөПӮ. (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 О’ 1 2 3 4
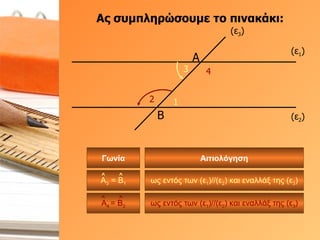
- 36. О‘ПӮ ПғП…ОјПҖО»О·ПҒПҺПғОҝП…ОјОө П„Оҝ ПҖО№ОҪОұОәО¬ОәО№: (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 3 4 О’ 1 2 О“ПүОҪОҜОұ О‘О№П„О№ОҝО»ПҢОіО·ПғО· ПүПӮ ОөОҪП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөОҪОұО»О»О¬Оҫ П„О·ПӮ (Оө 3 ) ПүПӮ ОөОҪП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөОҪОұО»О»О¬Оҫ П„О·ПӮ (Оө 3 ) О‘ 3 = О’ 1 О‘ 4 = О’ 2
- 37. О ОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ ПҖОҝП… П„ОӯОјОҪОҝОҪП„ОұО№ ОұПҖПҢ ОјОҜОұ О¬О»О»О· ОөП…ОёОөОҜОұ ОҹО№ ОөОҪП„ПҢПӮ вҖ“ ОөОәП„ПҢПӮ ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ ОіПүОҪОҜОөПӮ ОөОҜОҪОұО№ ОҜПғОөПӮ. (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 О’ 1 2 3 4
- 38. О‘ПӮ ПғП…ОјПҖО»О·ПҒПҺПғОҝП…ОјОө П„Оҝ ПҖО№ОҪОұОәО¬ОәО№. (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 3 4 О’ 1 2 О“ПүОҪОҜОұ О‘О№П„О№ОҝО»ПҢОіО·ПғО· ПүПӮ ОөОҪП„ПҢПӮ - ОөОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө 3 ) ПүПӮ ОөОҪП„ПҢПӮ - ОөОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө 3 ) ПүПӮ ОөОҪП„ПҢПӮ - ОөОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө 3 ) ПүПӮ ОөОҪП„ПҢПӮ - ОөОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө 3 ) 1 2 3 4 О‘ 1 = О’ 1 О‘ 2 = О’ 2 О‘ 3 = О’ 3 О‘ 4 = О’ 4
- 39. О ОұПҒО¬О»О»О·О»ОөПӮ ОөП…ОёОөОҜОөПӮ ПҖОҝП… П„ОӯОјОҪОҝОҪП„ОұО№ ОұПҖПҢ ОјОҜОұ О¬О»О»О· ОөП…ОёОөОҜОұ О‘ОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ П„ОӯОјОҪОҝОҪП„ОұО№ ОұПҖПҢ ОјОҜОұ О¬О»О»О· ОөП…ОёОөОҜОұ (Оө 3 ) П„ПҢП„Оө ПҢО»ОөПӮ ОҝО№ ОҝОҫОөОҜОөПӮ ОіПүОҪОҜОөПӮ ПҖОҝП… ПғПҮО·ОјОұП„ОҜО¶ОҝОҪП„ОұО№ ОөОҜОҪОұО№ ОҜПғОөПӮ ОәОұО№ ПҢО»ОөПӮ ОҝО№ ОұОјОІО»ОөОҜОөПӮ ОөОҜОҪОұО№ ОәОұО№ ОұП…П„ОӯПӮ ОҜПғОөПӮ ОјОөП„ОұОҫПҚ П„ОҝП…ПӮ. (Оө 1 ) (Оө 2 ) (Оө 3 )
- 40. ОҡОұО№ П„ПҺПҒОұ вҖҰ ОөОҜОҪОұО№ ПҺПҒОұ ОіО№Оұ ПҖОұПҒОұОҙОөОҜОіОјОұП„ОұвҖҰ
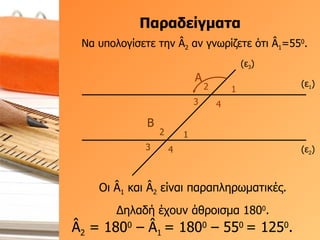
- 41. О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 О’ 1 2 3 4 ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О·ОҪ ГӮ 2 ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ ГӮ 1 =55 0 . ГӮ 2 = 180 0 вҖ“ ГӮ 1 = 180 0 вҖ“ 55 0 = 125 0 . ОҹО№ ГӮ 1 ОәОұО№ ГӮ 2 ОөОҜОҪОұО№ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ. О”О·О»ОұОҙО® ОӯПҮОҝП…ОҪ О¬ОёПҒОҝО№ПғОјОұ 180 0 .
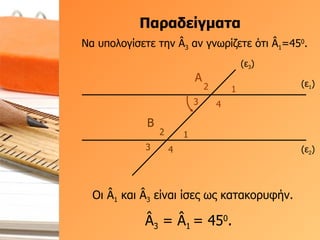
- 42. О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 О’ 1 2 3 4 ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О·ОҪ ГӮ 3 ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ ГӮ 1 =45 0 . ГӮ 3 = ГӮ 1 = 45 0 . ОҹО№ ГӮ 1 ОәОұО№ ГӮ 3 ОөОҜОҪОұО№ ОҜПғОөПӮ ПүПӮ ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ.
- 43. О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 ОҘ 1 2 3 4 ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О·ОҪ Е¶ 2 ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ ГӮ 4 =135 0 . Е¶ 2 = ГӮ 4 = 135 0 . ОҹО№ Е¶ 2 ОәОұО№ ГӮ 4 ОөОҜОҪОұО№ ОҜПғОөПӮ ПүПӮ ОөОҪП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөОҪОұО»О»О¬Оҫ П„О·ПӮ (Оө 3 ).
- 44. О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 ОҘ 1 2 3 4 ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О·ОҪ Е¶ 1 ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ ГӮ 1 =67 0 . Е¶ 1 = ГӮ 1 = 67 0 . ОҹО№ Е¶ 1 ОәОұО№ ГӮ 1 ОөОҜОҪОұО№ ОҜПғОөПӮ ПүПӮ ОөОҪП„ПҢПӮ вҖ“ ОөОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө 3 ).
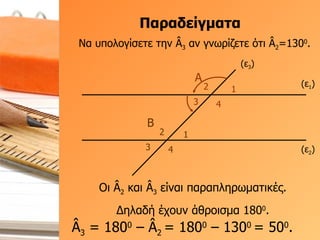
- 45. О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 О’ 1 2 3 4 ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О·ОҪ ГӮ 3 ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ ГӮ 2 =130 0 . ГӮ 3 = 180 0 вҖ“ ГӮ 2 = 180 0 вҖ“ 130 0 = 50 0 . ОҹО№ ГӮ 2 ОәОұО№ ГӮ 3 ОөОҜОҪОұО№ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ. О”О·О»ОұОҙО® ОӯПҮОҝП…ОҪ О¬ОёПҒОҝО№ПғОјОұ 180 0 .
- 46. О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 ОҘ 1 2 3 4 ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О·ОҪ Е¶ 3 ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ ГӮ 3 = 5 3 0 . Е¶ 3 = ГӮ 3 = 5 3 0 . ОҹО№ Е¶ 3 ОәОұО№ ГӮ 3 ОөОҜОҪОұО№ ОҜПғОөПӮ ПүПӮ ОөОҪП„ПҢПӮ вҖ“ ОөОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө 3 ).
- 47. О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 ОҘ 1 2 3 4 ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О·ОҪ ГӮ 4 ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ Е¶ 2 = 11 2 0 . ГӮ 4 = Е¶ 2 = 11 2 0 . ОҹО№ ГӮ 4 ОәОұО№ Е¶ 2 ОөОҜОҪОұО№ ОҜПғОөПӮ ПүПӮ ОөОҪП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөОҪОұО»О»О¬Оҫ П„О·ПӮ (Оө 3 ).
- 48. О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 ОҘ 1 2 3 4 ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О·ОҪ ГӮ 4 ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ Е¶ 4 = 142 0 . ГӮ 4 = Е¶ 4 = 142 0 . ОҹО№ ГӮ 4 ОәОұО№ Е¶ 4 ОөОҜОҪОұО№ ОҜПғОөПӮ ПүПӮ ОөОҪП„ПҢПӮ вҖ“ ОөОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө 3 ).
- 49. О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 ОҘ 1 2 3 4 ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О·ОҪ Е¶ 2 ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ Е¶ 4 = 108 0 . Е¶ 2 = Е¶ 4 = 108 0 . ОҹО№ Е¶ 2 ОәОұО№ Е¶ 4 ОөОҜОҪОұО№ ОҜПғОөПӮ ПүПӮ ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ.
- 50. О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 1 2 3 4 ОҘ 1 2 3 4 ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О·ОҪ Е¶ 2 ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ ГӮ 2 =115 0 . Е¶ 2 = ГӮ 2 = 115 0 . ОҹО№ Е¶ 2 ОәОұО№ ГӮ 2 ОөОҜОҪОұО№ ОҜПғОөПӮ ПүПӮ ОөОҪП„ПҢПӮ вҖ“ ОөОәП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө 3 ).
- 51. ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О№ПӮ ОіПүОҪОҜОөПӮ П„ОҝП… ПғПҮО®ОјОұП„ОҝПӮ ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ ГӮ 1 =60 0 . О ОұПҒОұОҙОөОҜОіОјОұП„Оұ О“ПүОҪОҜОұ О‘О№П„О№ОҝО»ПҢОіО·ПғО· ОұПҖПҢ П„О·ОҪ П…ПҖПҢОёОөПғО· ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ О‘ 1 = 60 0 (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 3 4 1 3 4 1 2 О’ 2 О‘ 2 =180 0 вҖ“ О‘ 1 = = 120 0 О ПүПӮ ОёОұ ОІПҒОҝПҚОјОө П„О·ОҪ О‘ 2 ;
- 52. ОқОұ П…ПҖОҝО»ОҝОіОҜПғОөП„Оө П„О№ПӮ ОіПүОҪОҜОөПӮ П„ОҝП… ПғПҮО®ОјОұП„ОҝПӮ ОұОҪ ОіОҪПүПҒОҜО¶ОөП„Оө ПҢП„О№ ГӮ 1 =60 0 . О ОұПҒОұОҙОөОҜОіОјОұП„Оұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ 3 4 О’ О“ПүОҪОҜОұ О‘О№П„О№ОҝО»ПҢОіО·ПғО· ОұПҖПҢ П„О·ОҪ П…ПҖПҢОёОөПғО· 1 2 3 4 1 2 ПүПӮ ПҖОұПҒОұПҖО»О·ПҒПүОјОұП„О№ОәОӯПӮ ПүПӮ ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ ПүПӮ ОөОҪП„ПҢПӮ вҖ“ ОөОәП„ПҢПӮ ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ ПүПӮ ОөОҪП„ПҢПӮ ОөОҪОұО»О»О¬Оҫ ПүПӮ ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ ПүПӮ ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ ПүПӮ ОәОұП„ОұОәОҝПҒП…ПҶО®ОҪ О”ОөОҪ ОөОҜОҪОұО№ ОұПҖОұПҒОұОҜП„О·П„Оҝ ОҪОұ ОөОҜОјОұПғП„Оө ОұОҪОұО»П…П„О№ОәОҝОҜ ОіО№Оұ П„О№ПӮ ОөП…ОёОөОҜОөПӮ ОіО№ОұП„ОҜ ОҙОөОҪ П…ПҖО¬ПҒПҮОөО№ ПҶПҢОІОҝПӮ ОҪОұ ОјПҖОөПҒОҙОөП…П„ОҝПҚОјОө. О‘ 1 = 60 0 О‘ 2 =180 0 вҖ“ О‘ 1 = = 120 0 О‘ 3 =О‘ 1 = 60 0 О‘ 4 =О‘ 2 = 120 0 О’ 1 =О‘ 1 = 60 0 О’ 2 = О‘ 4 = 120 0 О’ 3 =О’ 1 = 60 0 О’ 4 =О’ 2 = 120 0
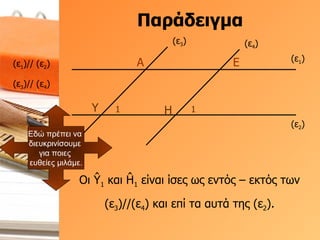
- 53. О ОұПҒО¬ОҙОөО№ОіОјОұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ ОҘ (Оө 4 ) О• О— (Оө 3 )// (Оө 4 ) (Оө 1 )// (Оө 2 ) 1 1 ОҹО№ Е¶ 1 ОәОұО№ ДӨ 1 ОөОҜОҪОұО№ ОҜПғОөПӮ ПүПӮ ОөОҪП„ПҢПӮ вҖ“ ОөОәП„ПҢПӮ П„ПүОҪ (Оө 3 )//(Оө 4 ) ОәОұО№ ОөПҖОҜ П„Оұ ОұП…П„О¬ П„О·ПӮ (Оө 2 ). О•ОҙПҺ ПҖПҒОӯПҖОөО№ ОҪОұ ОҙО№ОөП…ОәПҒО№ОҪОҜПғОҝП…ОјОө ОіО№Оұ ПҖОҝО№ОөПӮ ОөП…ОёОөОҜОөПӮ ОјО№О»О¬ОјОө.
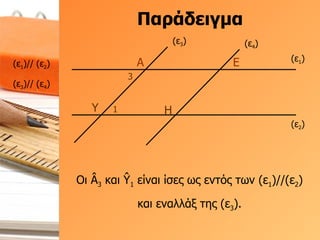
- 54. О ОұПҒО¬ОҙОөО№ОіОјОұ (Оө 1 ) (Оө 2 ) (Оө 3 ) О‘ ОҘ (Оө 4 ) О• О— (Оө 3 )// (Оө 4 ) (Оө 1 )// (Оө 2 ) 3 1 ОҹО№ ГӮ 3 ОәОұО№ Е¶ 1 ОөОҜОҪОұО№ ОҜПғОөПӮ ПүПӮ ОөОҪП„ПҢПӮ П„ПүОҪ (Оө 1 )//(Оө 2 ) ОәОұО№ ОөОҪОұО»О»О¬Оҫ П„О·ПӮ (Оө 3 ).
- 55. О•ПҒОіОұПғОҜОұ ОіО№Оұ П„Оҝ ОЈПҖОҜП„О№ ОҳОөПүПҒОҜОұ ОЈОөО». 214 -216 О‘ПғОәО®ПғОөО№ПӮ 2, 4 ПғОөО». 216