More Related Content Similar to Ю Я
ЮИЮБЮГЯЯЮЕЮЙЮП ЮИЮЕЯЯЮЗЮМЮБ - ЮИЯЯЮЏЮБ (20) More from ЮЌЯЮКЮЗЯЮЗ ЯЯ
ЮЛЮЛЮПЮГЮЎ ЮМЮБЮИЮЗЮМЮБЯЮЙЮКЯЮН ЮБЯЮКЮЎЯЮЕЯЮН (20)
1 5 ЮЕЯЯЯЮЕЯЮЙЮКЯ ЮГЮЙЮНЯЮМЮЕЮНЮП2 test 1 5 ЮЕЯЯЯЮЕЯЮЙЮКЯ ЮГЮЙЮНЯЮМЮЕЮНЮП2 test
ЮЌЯЮКЮЗЯЮЗ ЯЯ
ЮЛЮЛЮПЮГЮЎ ЮМЮБЮИЮЗЮМЮБЯЮЙЮКЯЮН ЮБЯЮКЮЎЯЮЕЯЮН Ь§
ЮЯЮПЯЮЕЮЏЯЮЕ ЮНЮБ ЮЕЯЮЙЯЮКЮЕЯЮИЮЕЮЏЯЮЕ ЯЮЗ ЯЮЕЮЛЮЏЮДЮБ http://www.askesi.blogspot.gr, ЮГЮЙЮБ ЮНЮБ ЮДЮЕЮЏЯЮЕ ЮЮНЮБ ЮДЮЙЮБЮГЯЮНЮЙЯЮМЮБ ЮДЮЙЮЌЯЮКЮЕЮЙЮБЯ ЮМЮЙЮБЯ ЮДЮЙЮДЮБЮКЯЮЙЮКЮЎЯ ЯЯЮБЯ ЯЯЮП ЮЕЯЯЯЮЕЯЮЙЮКЯ ЮГЮЙЮНЯЮМЮЕЮНЮП ЮДЮЙЮБЮНЯ
ЯЮМЮЌЯЯЮН ЮКЮБЮИЯЯ ЮКЮБЮЙ ЯЮЙЯ ЮЕЮНЮДЮЕЮЙЮКЯЮЙЮКЮЯ ЮЛЯЯЮЕЮЙЯ, ЯЯЮМЯЯЮНЮБ ЮМЮЕ ЯЮЗЮН ЯЮЛЮЗ ЯЯЮН ЮМЮБЮИЮЗЮМЮБЯЮЙЮКЯЮН ЯЯЮПЯЮБЮНЮБЯЮПЮЛЮЙЯЮМЮПЯ ЮЮ ЮЯ
ЮКЮЕЮЏЮПЯ
.
ТьЮПЮГЮБвЯЮЙЮИЮМЮПЮЙ ТьЮПЮГЮБвЯЮЙЮИЮМЮПЮЙ
ЮЌЯЮКЮЗЯЮЗ ЯЯ
ЮЛЮЛЮПЮГЮЎ ЮМЮБЮИЮЗЮМЮБЯЮЙЮКЯЮН ЮБЯЮКЮЎЯЮЕЯЮН Ь§
Ю ЮИЮЕЯЯЮЏЮБ ЯЯЮН ЮЛЮПЮГЮБЯЮЏЮИЮМЯЮН ЮКЮБЮЙ ЯЮЗЯ ЮЛЮПЮГЮБЯЮЙЮИЮМЮЙЮКЮЎЯ ЯЯ
ЮНЮЌЯЯЮЗЯЮЗЯ. Ю ЯЮБЯЮПЯ
ЯЮЏЮБЯЮЗ ЯЯ
ЮНЮПЮДЮЕЯЮЕЯЮБЮЙ ЮКЮБЮЙ ЮМЮЕ ЯЮП ЮБЮНЯЮЏЯЯЮПЮЙЯЮП ЯЯЮЛЮЛЮП ЮЕЯЮГЮБЯЮЏЮБЯ, ЯЮПЯ
ЮМЯЮПЯЮЕЮЏЯЮЕ ЮНЮБ ЮВЯЮЕЮЏЯЮЕ ЯЯЮП blog ЮМЮПЯ
ЯЯЮЗЮН ЮЕЮОЮЎЯ ЮДЮЙЮЕЯЮИЯ
ЮНЯЮЗ: www.askesi.blogspot.gr
2. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 1ЮЗ
ЮЃЯЮП ЮПЯЮКЮПЮГЯЮНЮЙЮП ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЯЮПЯ
ЮДЮЙЯЮЛЮБЮНЮПЯ ЯЯЮЙЮМЮБЯЮПЯ, ЮПЮЙ
ЮКЮЌЮКЮЕЯЮЕЯ ЯЮЛЮЕЯ
ЯЮЖЯ ЮЕЮЏЮНЮБЮЙ ЮПЮЙ тІтІ ЮКЮБЮЙ тІтІ ЮЕЮНЯ ЮИ Я
ЯЮПЯЮЕЮЏЮНЮПЯ
ЯЮБ
ЮЕЮЏЮНЮБЮЙ ЮИ тІтІ .
ЮЅЯЮПЮЛЮПЮГЮЏЯЯЮЕ ЯЮЙЯ ЯЮБЯЮБЮКЮЌЯЯ ЯЮБЯЮБЯЯЮЌЯЮЕЮЙЯ:
ЮЮ2 = тІтІтІтІтІтІтІтІтІтІтІтІтІтІтІтІ
ЮЮ2 + ЮЮ2 = тІтІтІтІтІтІтІтІтІтІтІтІтІ
3. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 1ЮЗ
ЮЃЯЮП ЮПЯЮКЮПЮГЯЮНЮЙЮП ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЯЮПЯ
ЮДЮЙЯЮЛЮБЮНЮПЯ ЯЯЮЙЮМЮБЯЮПЯ, ЮПЮЙ
ЮКЮЌЮКЮЕЯЮЕЯ ЯЮЛЮЕЯ
ЯЮЖЯ ЮЕЮЏЮНЮБЮЙ ЮПЮЙ ЮЮ ЮКЮБЮЙ ЮЮ ЮЕЮНЯ ЮИ Я
ЯЮПЯЮЕЮЏЮНЮПЯ
ЯЮБ
ЮЕЮЏЮНЮБЮЙ ЮИ ЮЮ .
ЮЅЯЮПЮЛЮПЮГЮЏЯЯЮЕ ЯЮЙЯ ЯЮБЯЮБЮКЮЌЯЯ ЯЮБЯЮБЯЯЮЌЯЮЕЮЙЯ:
ЮЮ2 = 52 = 25
ЮЮ2 + ЮЮ2 = 42 + 32 = 16+9 = 25
4. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 1ЮЗ
ЮЃЯЮП ЮПЯЮКЮПЮГЯЮНЮЙЮП ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЯЮПЯ
ЮДЮЙЯЮЛЮБЮНЮПЯ ЯЯЮЙЮМЮБЯЮПЯ, ЮПЮЙ
ЮКЮЌЮКЮЕЯЮЕЯ ЯЮЛЮЕЯ
ЯЮЖЯ ЮЕЮЏЮНЮБЮЙ ЮПЮЙ ЮЮ ЮКЮБЮЙ ЮЮ ЮЕЮНЯ ЮИ Я
ЯЮПЯЮЕЮЏЮНЮПЯ
ЯЮБ
ЮЕЮЏЮНЮБЮЙ ЮИ ЮЮ .
ЮЅЯЮПЮЛЮПЮГЮЏЯЯЮЕ ЯЮЙЯ ЯЮБЯЮБЮКЮЌЯЯ ЯЮБЯЮБЯЯЮЌЯЮЕЮЙЯ:
ЮЮ2 = 52 = 25
ЮЮ2 + ЮЮ2 = 42 + 32 = 16+9 = 25
ЮЮМЮПЮЏЯЯ ЮГЮЙЮБ ЯЮП ЮДЮЙЯЮЛЮБЮНЯ ЮПЯЮКЮПЮГЯЮНЮЙЮП ЯЯЮЏЮГЯЮНЮП ЯЯЮЙЮМЮБ ЮНЮБ
ЯЯЮПЯЮДЮЙЮПЯЮЏЯЮЕЯЮЕ ЮКЮБЮЙ ЯЮЌЮЛЮЙ ЯЮЙЯ ЯЮБЯЮБЯЯЮЌЯЮЕЮЙЯ:
ЮЮ2 = тІтІтІтІтІтІтІтІтІтІтІтІтІтІтІ
ЮЮ2 + ЮЮ2 = тІтІтІтІтІтІтІтІтІтІтІтІтІтІтІ
5. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 1ЮЗ
ЮЃЯЮП ЮПЯЮКЮПЮГЯЮНЮЙЮП ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЯЮПЯ
ЮДЮЙЯЮЛЮБЮНЮПЯ ЯЯЮЙЮМЮБЯЮПЯ, ЮПЮЙ
ЮКЮЌЮКЮЕЯЮЕЯ ЯЮЛЮЕЯ
ЯЮЖЯ ЮЕЮЏЮНЮБЮЙ ЮПЮЙ ЮЮ ЮКЮБЮЙ ЮЮ ЮЕЮНЯ ЮИ Я
ЯЮПЯЮЕЮЏЮНЮПЯ
ЯЮБ
ЮЕЮЏЮНЮБЮЙ ЮИ ЮЮ .
ЮЅЯЮПЮЛЮПЮГЮЏЯЯЮЕ ЯЮЙЯ ЯЮБЯЮБЮКЮЌЯЯ ЯЮБЯЮБЯЯЮЌЯЮЕЮЙЯ:
ЮЮ2 = 52 = 25
ЮЮ2 + ЮЮ2 = 42 + 32 = 16+9 = 25
ЮЮМЮПЮЏЯЯ ЮГЮЙЮБ ЯЮП ЮДЮЙЯЮЛЮБЮНЯ ЮПЯЮКЮПЮГЯЮНЮЙЮП ЯЯЮЏЮГЯЮНЮП ЯЯЮЙЮМЮБ ЮНЮБ
ЯЯЮПЯЮДЮЙЮПЯЮЏЯЮЕЯЮЕ ЮКЮБЮЙ ЯЮЌЮЛЮЙ ЯЮЙЯ ЯЮБЯЮБЯЯЮЌЯЮЕЮЙЯ:
ЮЮ2 = 152 = 225
ЮЮ2 + ЮЮ2 = 122 + 92 = 144+81 = 225
6. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 1ЮЗ
ЮЃЯЮП ЮДЮЙЯЮЛЮБЮНЯ ЯЯЮЙЮМЮБ ЮКЮБЯЮБЯЮКЮЕЯ
ЮЌЯЮБЮМЮЕ ЮБЯЯЮЙЮКЮЌ ЯЮП ЮПЯЮКЮПЮГЯЮНЮЙЮП
ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЮКЮБЮЙ ЮЕЮОЯЯЮЕЯЮЙЮКЮЌ ЯЮПЯ
, ЮКЮБЯЮБЯЮКЮЕЯ
ЮЌЯЮБЮМЮЕ ЯЮЕЯЯЮЌЮГЯЮНЮБ, ЯЮПЯ
ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮЖЯЮЕЮЙ ЯЯ ЯЮЛЮЕЯ
ЯЮЌ ЮМЮЏЮБ ЯЮЛЮЕЯ
ЯЮЌ ЯЮПЯ
ЯЯЮЙЮГЯЮНЮПЯ
.
ЮЅЯЮПЮЛЮПЮГЮЏЯЯЮЕ ЯЮБ ЮЕЮМЮВЮБЮДЮЌ ЯЯЮН ЯЮЕЯЯЮБЮГЯЮНЯЮН:
(ЮЮЮЮ) = тІтІтІтІтІтІтІтІтІтІтІтІтІ
(ЮЮЮЮ) = тІтІтІтІтІтІтІтІтІтІтІтІтІ
(ЮЮЮЮ) = тІтІтІтІтІтІтІтІтІтІтІтІтІ
7. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 1ЮЗ
ЮЃЯЮП ЮДЮЙЯЮЛЮБЮНЯ ЯЯЮЙЮМЮБ ЮКЮБЯЮБЯЮКЮЕЯ
ЮЌЯЮБЮМЮЕ ЮБЯЯЮЙЮКЮЌ ЯЮП ЮПЯЮКЮПЮГЯЮНЮЙЮП
ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЮКЮБЮЙ ЮЕЮОЯЯЮЕЯЮЙЮКЮЌ ЯЮПЯ
, ЮКЮБЯЮБЯЮКЮЕЯ
ЮЌЯЮБЮМЮЕ ЯЮЕЯЯЮЌЮГЯЮНЮБ, ЯЮПЯ
ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮЖЯЮЕЮЙ ЯЯ ЯЮЛЮЕЯ
ЯЮЌ ЮМЮЏЮБ ЯЮЛЮЕЯ
ЯЮЌ ЯЮПЯ
ЯЯЮЙЮГЯЮНЮПЯ
.
ЮЅЯЮПЮЛЮПЮГЮЏЯЯЮЕ ЯЮБ ЮЕЮМЮВЮБЮДЮЌ ЯЯЮН ЯЮЕЯЯЮБЮГЯЮНЯЮН:
(ЮЮЮЮ) = 102 = 100
(ЮЮЮЮ) = 82 = 64
(ЮЮЮЮ) = 62 = 36
8. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 1ЮЗ
ЮЃЯЮП ЮДЮЙЯЮЛЮБЮНЯ ЯЯЮЙЮМЮБ ЮКЮБЯЮБЯЮКЮЕЯ
ЮЌЯЮБЮМЮЕ ЮБЯЯЮЙЮКЮЌ ЯЮП ЮПЯЮКЮПЮГЯЮНЮЙЮП
ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЮКЮБЮЙ ЮЕЮОЯЯЮЕЯЮЙЮКЮЌ ЯЮПЯ
, ЮКЮБЯЮБЯЮКЮЕЯ
ЮЌЯЮБЮМЮЕ ЯЮЕЯЯЮЌЮГЯЮНЮБ, ЯЮПЯ
ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮЖЯЮЕЮЙ ЯЯ ЯЮЛЮЕЯ
ЯЮЌ ЮМЮЏЮБ ЯЮЛЮЕЯ
ЯЮЌ ЯЮПЯ
ЯЯЮЙЮГЯЮНЮПЯ
.
ЮЅЯЮПЮЛЮПЮГЮЏЯЯЮЕ ЯЮБ ЮЕЮМЮВЮБЮДЮЌ ЯЯЮН ЯЮЕЯЯЮБЮГЯЮНЯЮН:
(ЮЮЮЮ) = 102 = 100
(ЮЮЮЮ) = 82 = 64
(ЮЮЮЮ) = 62 = 36
Ю ЮПЮЙЮБ ЯЯЮЖЯЮИ ЯЯ
ЮНЮДЮЖЮЕЮЙ ЯЮЙЯ ЯЮЛЮЕЯ
ЯЮЖЯ ЯЮПЯ
ЯЯЮЙЮГЯЮНЮПЯ
ЮЮЮ;
9. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 1ЮЗ
ЮЃЯЮП ЮДЮЙЯЮЛЮБЮНЯ ЯЯЮЙЮМЮБ ЮКЮБЯЮБЯЮКЮЕЯ
ЮЌЯЮБЮМЮЕ ЮБЯЯЮЙЮКЮЌ ЯЮП ЮПЯЮКЮПЮГЯЮНЮЙЮП
ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЮКЮБЮЙ ЮЕЮОЯЯЮЕЯЮЙЮКЮЌ ЯЮПЯ
, ЮКЮБЯЮБЯЮКЮЕЯ
ЮЌЯЮБЮМЮЕ ЯЮЕЯЯЮЌЮГЯЮНЮБ, ЯЮПЯ
ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮЖЯЮЕЮЙ ЯЯ ЯЮЛЮЕЯ
ЯЮЌ ЮМЮЏЮБ ЯЮЛЮЕЯ
ЯЮЌ ЯЮПЯ
ЯЯЮЙЮГЯЮНЮПЯ
.
ЮЅЯЮПЮЛЮПЮГЮЏЯЯЮЕ ЯЮБ ЮЕЮМЮВЮБЮДЮЌ ЯЯЮН ЯЮЕЯЯЮБЮГЯЮНЯЮН:
(ЮЮЮЮ) = 102 = 100
(ЮЮЮЮ) = 82 = 64
(ЮЮЮЮ) = 62 = 36
Ю ЮПЮЙЮБ ЯЯЮЖЯЮИ ЯЯ
ЮНЮДЮЖЮЕЮЙ ЯЮЙЯ ЯЮЛЮЕЯ
ЯЮЖЯ ЯЮПЯ
ЯЯЮЙЮГЯЮНЮПЯ
ЮЮЮ;
Ю ЮБЯЮБЯЮЗЯЮПЯЮМЮЕ ЯЯЮЙ:
(ЮЮЮЮ) = (ЮЮЮЮ)+(ЮЮЮЮ) я ЮЮ2 = ЮЮ2 + ЮЮ2
10. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 1ЮЗ
ЮЃЯЮП ЮДЮЙЯЮЛЮБЮНЯ ЯЯЮЙЮМЮБ ЮКЮБЯЮБЯЮКЮЕЯ
ЮЌЯЮБЮМЮЕ ЮБЯЯЮЙЮКЮЌ ЯЮП ЮПЯЮКЮПЮГЯЮНЮЙЮП
ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЮКЮБЮЙ ЮЕЮОЯЯЮЕЯЮЙЮКЮЌ ЯЮПЯ
, ЮКЮБЯЮБЯЮКЮЕЯ
ЮЌЯЮБЮМЮЕ ЯЮЕЯЯЮЌЮГЯЮНЮБ, ЯЮПЯ
ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮЖЯЮЕЮЙ ЯЯ ЯЮЛЮЕЯ
ЯЮЌ ЮМЮЏЮБ ЯЮЛЮЕЯ
ЯЮЌ ЯЮПЯ
ЯЯЮЙЮГЯЮНЮПЯ
.
ЮЅЯЮПЮЛЮПЮГЮЏЯЯЮЕ ЯЮБ ЮЕЮМЮВЮБЮДЮЌ ЯЯЮН ЯЮЕЯЯЮБЮГЯЮНЯЮН:
(ЮЮЮЮ) = 102 = 100
(ЮЮЮЮ) = 82 = 64
(ЮЮЮЮ) = 62 = 36
Ю ЮПЮЙЮБ ЯЯЮЖЯЮИ ЯЯ
ЮНЮДЮЖЮЕЮЙ ЯЮЙЯ ЯЮЛЮЕЯ
ЯЮЖЯ ЯЮПЯ
ЯЯЮЙЮГЯЮНЮПЯ
ЮЮЮ;
Ю ЮБЯЮБЯЮЗЯЮПЯЮМЮЕ ЯЯЮЙ:
(ЮЮЮЮ) = (ЮЮЮЮ)+(ЮЮЮЮ) я ЮЮ2 = ЮЮ2 + ЮЮ2
ЮЄЮЙ ЯЮБЯЮБЯЮЗЯЮЕЮЏЯЮЕ ЯЯЮЙ ЮЙЯЯЯЮЕЮЙ ЯЯЮБ ЮПЯЮИЮПЮГЯЮНЮЙЮБ ЯЯЮЏЮГЯЮНЮБ;
11. Ю ЯЮИЮБЮГЯЯЮЕЮЙЮП ЮИЮЕЯЯЮЗЮМЮБ
ЮЃЮЕ ЮКЮЌЮИЮЕ ЮПЯЮИЮПЮГЯЮНЮЙЮП ЮЗЯЮЏЮГЯЮНЮП, ЮЗЮП ЮЗЮЕЮЗЯЮЌЮГЯЮНЮП ЮЗЮЗЯ
ЯЯЮПЮЗЮЕЮЏЮНЮПЯЮЖЮБЯ ЮЙЮЖЮПЯЮЗЮБЮЙ ЮМЮЕ ЮЗЮП ЮЌЮИЯЮПЮЙЮЖЮМЮБ ЮЗЯЮН
ЮЗЮЕЮЗЯЮБЮГЯЮНЯЮН ЮЗЯЮН ЮДЯЮП ЮКЮБЮИЮЮЗЯЮН ЯЮЛЮЕЯЯЯЮН
ЮЮ2 = ЮЮ2 + ЮЮ2
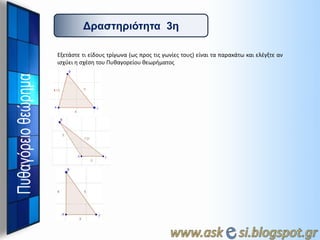
20. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 3ЮЗ
ЮЮОЮЕЯЮЌЯЯЮЕ ЯЮЙ ЮЕЮЏЮДЮПЯ
Я ЯЯЮЏЮГЯЮНЮБ (ЯЯ ЯЯЮПЯ ЯЮЙЯ ЮГЯЮНЮЏЮЕЯ ЯЮПЯ
Я) ЮЕЮЏЮНЮБЮЙ ЯЮБ ЯЮБЯЮБЮКЮЌЯЯ ЮКЮБЮЙ ЮЕЮЛЮЖЮГЮОЯЮЕ ЮБЮН
ЮЙЯЯЯЮЕЮЙ ЮИ ЯЯЮЖЯЮИ ЯЮПЯ
Ю Я
ЮКЮБЮГЮПЯЮЕЮЏЮПЯ
ЮКЮЕЯЯЮЙЮМЮБЯЮПЯ
21. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 3ЮЗ
ЮЮОЮЕЯЮЌЯЯЮЕ ЯЮЙ ЮЕЮЏЮДЮПЯ
Я ЯЯЮЏЮГЯЮНЮБ (ЯЯ ЯЯЮПЯ ЯЮЙЯ ЮГЯЮНЮЏЮЕЯ ЯЮПЯ
Я) ЮЕЮЏЮНЮБЮЙ ЯЮБ ЯЮБЯЮБЮКЮЌЯЯ ЮКЮБЮЙ ЮЕЮЛЮЖЮГЮОЯЮЕ ЮБЮН
ЮЙЯЯЯЮЕЮЙ ЮИ ЯЯЮЖЯЮИ ЯЮПЯ
Ю Я
ЮКЮБЮГЮПЯЮЕЮЏЮПЯ
ЮКЮЕЯЯЮЙЮМЮБЯЮПЯ
ЮПЮОЯЮГЯЮНЮЙЮП
ЮЮ2 < ЮЮ2 + ЮЮ2
22. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 3ЮЗ
ЮЮОЮЕЯЮЌЯЯЮЕ ЯЮЙ ЮЕЮЏЮДЮПЯ
Я ЯЯЮЏЮГЯЮНЮБ (ЯЯ ЯЯЮПЯ ЯЮЙЯ ЮГЯЮНЮЏЮЕЯ ЯЮПЯ
Я) ЮЕЮЏЮНЮБЮЙ ЯЮБ ЯЮБЯЮБЮКЮЌЯЯ ЮКЮБЮЙ ЮЕЮЛЮЖЮГЮОЯЮЕ ЮБЮН
ЮЙЯЯЯЮЕЮЙ ЮИ ЯЯЮЖЯЮИ ЯЮПЯ
Ю Я
ЮКЮБЮГЮПЯЮЕЮЏЮПЯ
ЮКЮЕЯЯЮЙЮМЮБЯЮПЯ
ЮПЮОЯЮГЯЮНЮЙЮП
ЮЮ2 < ЮЮ2 + ЮЮ2
ЮБЮМЮВЮЛЯЮГЯЮНЮЙЮП
ЮЮ2 > ЮЮ2 + ЮЮ2
23. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 3ЮЗ
ЮЮОЮЕЯЮЌЯЯЮЕ ЯЮЙ ЮЕЮЏЮДЮПЯ
Я ЯЯЮЏЮГЯЮНЮБ (ЯЯ ЯЯЮПЯ ЯЮЙЯ ЮГЯЮНЮЏЮЕЯ ЯЮПЯ
Я) ЮЕЮЏЮНЮБЮЙ ЯЮБ ЯЮБЯЮБЮКЮЌЯЯ ЮКЮБЮЙ ЮЕЮЛЮЖЮГЮОЯЮЕ ЮБЮН
ЮЙЯЯЯЮЕЮЙ ЮИ ЯЯЮЖЯЮИ ЯЮПЯ
Ю Я
ЮКЮБЮГЮПЯЮЕЮЏЮПЯ
ЮКЮЕЯЯЮЙЮМЮБЯЮПЯ
ЮПЮОЯЮГЯЮНЮЙЮП
ЮЮ2 < ЮЮ2 + ЮЮ2
ЮБЮМЮВЮЛЯЮГЯЮНЮЙЮП
ЮЮ2 > ЮЮ2 + ЮЮ2
ЮПЯЮИЮПЮГЯЮНЮЙЮП
ЮЮ2 = ЮЮ2 + ЮЮ2
27. ЮЮНЮЗЮЏЮЖЮЗЯЮПЮИЮП Ю ЯЮИЮБЮГЮПЯЮЕЮЏЮПЯ ЮИЮЕЯЯЮЎЮМЮБЮЗЮПЯ
ЮЮН ЮЖЮЕ ЮЮНЮБ ЮЗЯЮЏЮГЯЮНЮП, ЮЗЮП ЮЗЮЕЮЗЯЮЌЮГЯЮНЮП ЮЗЮЗЯ ЮМЮЕЮГЮБЮЛЯЮЗЮЕЯЮЗЯ
ЯЮЛЮЕЯЯЮЌЯ ЮЙЮЖЮПЯЮЗЮБЮЙ ЮМЮЕ ЮЗЮП ЮЌЮИЯЮПЮЙЮЖЮМЮБ ЮЗЯЮН ЮЗЮЕЮЗЯЮБЮГЯЮНЯЮН ЮЗЯЮН
ЮДЯЮП ЮЌЮЛЮЛЯЮН ЯЮЛЮЕЯЯЯЮН, ЮЗЯЮЗЮЕ ЮЗЮП ЮЗЯЮЏЮГЯЮНЮП ЮЕЮЏЮНЮБЮЙ ЮПЯЮИЮПЮГЯЮНЮЙЮП
ЮМЮЕ ЯЯЮПЮЗЮЕЮЏЮНЮПЯЮЖЮБ ЮЗЮЗ ЮМЮЕЮГЮБЮЛЯЮЗЮЕЯЮЗ ЯЮЛЮЕЯЯЮЌ
29. ЮЯЮБЮЖЮЗЮЗЯЮЙЯЮЗЮЗЮЗЮБ 4ЮЗ
ЮЃЯЮП ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБ, ЯЮП ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЮЖЯЮЕЮЙ ЯЮЕЯЮЏЮМЮЕЯЯЮП 150 m.
ЮБ) ЮЮБ ЮВЯЮЕЮЏЯЮЕ ЯЮПЮН ЮБЯЮЙЮКЮМЯ x.
ЮВ) ЮЮБ ЮБЯЮПЮДЮЕЮЏЮОЮЕЯЮЕ ЯЯЮЙ ЯЮП ЯЯЮЏЮГЯЮНЮП ЮЮЮ ЮЕЮЏЮНЮБЮЙ ЮПЯЮКЮПЮГЯЮНЮЙЮП.