![DPによる解法
? Sijの最適な部分集合の数を c[i,j] とすると，?
?](https://image.slidesharecdn.com/ia16-140510070944-phpapp02/85/IA16-7-320.jpg)
![ハフマン符号が最適であるこ
との証明(3)
? Theorem16.4?
ハフマン符号は最適な接頭符号を生成する
? [証] Lamma16.2及び16.3 から直ちに示される](https://image.slidesharecdn.com/ia16-140510070944-phpapp02/85/IA16-36-320.jpg)
IA16
- 1. Introduction to Algorithms Chapter 16? Greedy Algorithm
- 2. 貪欲法 ? 多くの最適化問題でDPはoverkill? => 貪欲法 ? 貪欲法ではある時点で最も良いものを選んでいく ? 必ず最適解が得られる訳ではないが，うまく行く事 も多い
- 3. 16.1 An activity-selection problem ? n個のactivityの集合 S = {a1,a2,…,an} ? 各aiは開始時刻siと終了時刻?が決まっている ? 決められた時間の中で各activityが重ならないとい う条件のもとで最も多くのactivityが実行できるよ うなSの部分集合を求めたい
- 4. 問題例 ? 例えば{a3, a9, a11} はそれぞれ重なることがない ? {a1, a4, a8, a11} もしくは {a2, a4, a9, a11} が重 ならないでかつactivityの数が最大となる集合
- 5. 問題の分解 ? Sij を ai が終了し，ajが始まるまでのactivityの集合とす る ? お互い重ならないでactivity数が最大のSijの部分集合を求 めたい．そのような集合をAijとする ? あるactivity ak がAijに含まれるとする．すると，残りは? 1. Sik(aiより後，akより前に終わるactivityの集合)と，? 2. Skj(akより後，ajより前に終わるactivityの集合) ? の集合の中で最も良い部分集合を求める問題になる
- 6. 問題の分解 ? Aik = Aij Sik? Akj = Aij Skj? ? => Aij = Aik {ak} Akj? ?Aij? = ?Aik? + ?Akj? + 1
- 7. DPによる解法 ? Sijの最適な部分集合の数を c[i,j] とすると，? ?
- 8. 貪欲法で考える ? 全ての部分問題を解く必要があるのか？ ? 実は，この問題ではある時点においてactivityを選 択するとき，可能な候補の中で最も早く終了するも のを選べば良い (貪欲的選択) ? 貪欲的選択であるactivity ak を選んだ場合，残る 部分問題は1つ (ak終了時刻よりあとのactivityの集 合の中から最適な部分集合を選ぶ)
- 10. 証明 ? Ak: Skの中で重ならない最大の部分集合 ? aj : Akの中で最も早く終わるもの ? aj = am なら終了 ? aj != am なら A k = Ak - {aj} {am} とajとamを入 れ替える． すると，Akはお互いに重ならず，amはaj より早く終了するのでA kもお互いに重ならず，?A k? = ?Ak?. つまりSkの最適な部分集合はamを含む
- 11. 結論 ? activity-seleciton 問題は貪欲法で最適解が求めら れる ? 貪欲法は基本的にトップダウン的? ある選択をしてから，次の部分問題を特? (DPは，部分問題を解いてから選択をするボトムアッ プ式)
- 12. 再帰的貪欲法 ? ボトムアップ式に考える? ? ? ? ? s,f: 各activityの開始/終了時間の配列(ソート済)? k=0からはじめてk=nの部分問題を解いて終了 ? 全体として各acitivityは1回ずつ調べられるのでΘ(n)
- 14. 貪欲法による解の構成方法 1. 問題の最適な構造を決定する 2. 再帰的な解法を考える 3. その時貪欲的選択をした場合一つの部分問題だけ残ること を示す 4. 常に貪欲的選択をしても問題ないことを示す 5. 貪欲的な再帰的解法を実装する 6. 再帰的解法をループに変換する
- 15. もう少し単純化すると 1. 問題をある一つの選択をした場合，一つの部分問 題が残るような形で表現する 2. 最適な解の中で貪欲的選択をするものがある事を 示す 3. 貪欲的選択をし，残りの部分問題も同様に貪欲的 選択をしていくことで最適解が構成できることを 示す
- 16. いつ貪欲法が使えるか? ? 残念ながら単純に分かる方法はない ? ただし，貪欲的選択属性 (Greedy-choise property) と 最適部分構造 (optimal substructure) の2つが重要
- 17. Greedy-choise property ? ある時点で最適な選択をすれば結果として最適解が 得られる事 ? 一般にDPでは，部分問題を解かなければ選択を決定 できない? => ボトムアップで解く．トップダウンにしたければ メモ化する ? 貪欲法では選択は部分問題によらない? => トップダウン
- 18. Optimal substructure ? 最適解が部分問題の最適解を含む事 ? 貪欲的選択をしたとき，残りの部分問題の最適解を 合わせたものが最適解になるか考えることが必要
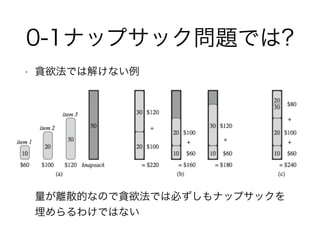
- 19. 貪欲法 vs DP ? 以下の2つの問題を考える ? 0-1 ナップサック問題? n個の商品があり，i番目の商品は価値vi,重さwi? Σwi W の制限かでviを最大化する商品集合は? ? 分数ナップサック問題? 0-1ナップサック問題と似ているが，商品の個数が 分数で良い
- 20. ナップサック問題の性質 ? 両方ともoptimal-substructure 属性を持つ ? 0-1ナップサック問題において，合計の重さがWの最 適解の中からある商品jを取り除いたとする．すると 残りのW-wjの重さの商品はn-1個の商品集合の中か ら選んだ最適解 ? 分数ナップサック問題では，jを重さwだけ取り除く と残りのW-wの商品集合はn-1個の商品集合と重さwj- w のjの中から選んだ最適集合
- 22. 分数ナップサック問題の解法 1. vi/wi を計算する 2. 貪欲的にvi/wiが最も高い商品から選んでいく ? 証明はExercise 16.2-1
- 24. 16.3 ハフマン符号 ? 符号化: a,b,cなどの文字を01で表現すること ? 文字符号化問題? 平均符号長をできるだけ短くして文字を符号化する? 文字の生成頻度は一般に異なるので上手くやれば効率 的な符号化ができる => ハフマン符号? ? ? ?
- 25. 接頭符号(pre?x code) ? ある符号語の接頭語が他の符号語になっていないこ と? ex) 1110 という符号語があったとき， 111 とい う符号語が別にあればそれは接頭符号でない ? 接頭符号なら，一意にデコード可能
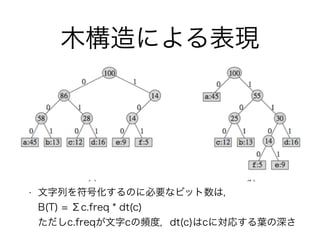
- 26. 木構造による表現 ? 文字列を符号化するのに必要なビット数は，? B(T) = Σc.freq * dt(c)? ただしc.freqが文字cの頻度，dt(c)はcに対応する葉の深さ
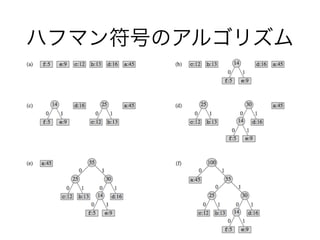
- 27. ハフマン符号の構成 ? ハフマン符号は，貪欲的方法で最適な接頭符号を背 生成する ? アイディア: 先ほどの木构造を叶から构成する
- 28. ハフマン符号のアルゴリズム
- 29. ハフマン符号のアルゴリズム ? C: n個の文字の集合, c C, c.freq: cの頻度とする ? Qは頻度を基準とするプライオリティーキュー? ? ? ? ?
- 30. ハフマン符号が最適であるこ との証明(1) ? Lemma 16.2? Cを文字集合，c C の頻度をc.freqとする．? xとyがCの中で最も頻度が低い文字のいずれかだと すると，xとyの符号語の長さが同じでかつxとyの 最後のビットだけ異なるような最適な符号が存在す る? ? これはハフマン符号がgreedy-choise属性を持つ事 を示す
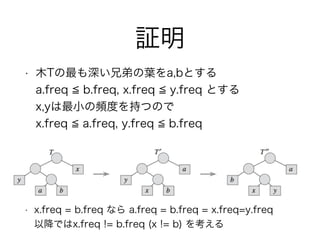
- 32. 証明 ? 木Tの最も深い兄弟の葉をa,bとする? a.freq b.freq, x.freq y.freq とする? x,yは最小の頻度を持つので? x.freq a.freq, y.freq b.freq ? x.freq = b.freq なら a.freq = b.freq = x.freq=y.freq? 以降ではx.freq != b.freq (x != b) を考える
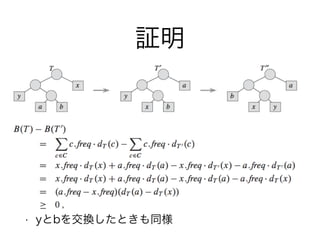
- 34. ハフマン符号が最適であるこ との証明(2) ? Lemma 16.3? Cを文字集合，c C の頻度をc.freqとする．? xとyをCの中で最小の頻度を持つ2つの文字とする.? C = C - {x,y} {z} を考える．z.freq = x.freq + y.freq.? T をC を表現する最適な符号語の一つだとすると， T の葉ノードzをxとyを子に持つようなノードに変 更したTはCの最適な符号語になる
- 35. 証明 ? x,y を除いて dT(c) = dT (c) (深さが同じ) ? dT(x) = dT (z)+1, dT(y) = dT (z)+1 ? x.freq*dT(x) + y.freq*dT(y) = z.freq*dT (z) + x.freq + y.freq ? B(T) = B(T ) + x.freq + y.freq ? Tが最適でなければ B(T ) < B(T) になるT が存在? Lemma16.2よりT はxとyを葉ノードに持つような木T にできる? B(T ) = B(T ) - x.freq - y.freq < B(T) - x.freq - y.freq = B(T )
- 36. ハフマン符号が最適であるこ との証明(3) ? Theorem16.4? ハフマン符号は最適な接頭符号を生成する ? [証] Lamma16.2及び16.3 から直ちに示される