Intervale numere reale
- 2. Intervale mărginite Fie a,b R∊ , a≤b şi A(a) respectiv B(b) , punctele corespunzătoare pe axa numerică A(a ) ∞− ∞+ B(b ) Definim următoarele mulţimi de numere reale: Interval închis cu extremităţile a, b: [ ] { }bxaRxba ≤≤∈=, X(x )
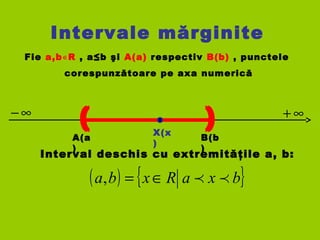
- 3. Intervale mărginite Fie a,b R∊ , a≤b şi A(a) respectiv B(b) , punctele corespunzătoare pe axa numerică A(a ) ∞− ∞+ B(b ) Interval deschis cu extremităţile a, b: ( ) { }bxaRxba ∈=, X(x )
- 4. Intervale mărginite Fie a,b R∊ , a≤b şi A(a) respectiv B(b) , punctele corespunzătoare pe axa numerică A(a ) ∞− ∞+ B(b ) Interval semideschis cu extremităţile a, b, [ ) { }bxaRxba ≤∈=, închis la stânga şi deschis la dreapta: X(x )
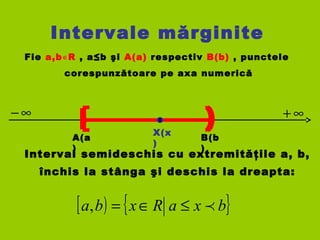
- 5. Intervale mărginite Fie a,b R∊ , a≤b şi A(a) respectiv B(b) , punctele corespunzătoare pe axa numerică A(a ) ∞− ∞+ B(b ) Interval semideschis cu extremităţile a, b, ( ] { }bxaRxba ≤∈= , deschis la stânga şi închis la dreapta: X(x )
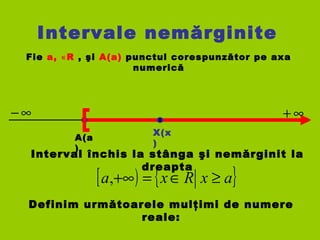
- 6. Intervale nemărginite Fie a, R∊ , şi A(a) punctul corespunzător pe axa numerică A(a ) ∞− ∞+ Definim următoarele mulţimi de numere reale: Interval închis la stânga şi nemărginit la dreapta [ ) { }axRxa ≥∈=+∞, X(x )
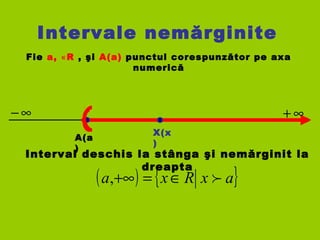
- 7. Intervale nemărginite Fie a, R∊ , şi A(a) punctul corespunzător pe axa numerică A(a ) ∞− ∞+ Interval deschis la stânga şi nemărginit la dreapta ( ) { }axRxa ∈=+∞, X(x )
- 8. Intervale nemărginite Fie a, R∊ , şi A(a) punctul corespunzător pe axa numerică ∞− ∞+ Interval inchis la dreapta şi nemărginit la stânga ( ] { }axRxa ≤∈=∞− , A(a ) X(x )
- 9. Intervale nemărginite Fie a, R∊ , şi A(a) punctul corespunzător pe axa numerică ∞− ∞+ Interval deschis la dreapta şi nemărginit la stânga ( ) { }axRxa ∈=∞− , A(a ) X(x )
- 10. Intervale nemărginite Fie a, R∊ , şi A(a) punctul corespunzător pe axa numerică ∞− ∞+ Interval deschis la dreapta şi nemărginit la stânga ( ) { }axRxa ∈=∞− , A(a ) X(x )

![Intervale mărginite
Fie a,b R∊ , a≤b şi A(a) respectiv B(b) , punctele
corespunzătoare pe axa numerică
A(a
)
‚àû‚àí ‚àû+
B(b
)
Definim următoarele mulţimi de numere
reale:
Interval închis cu extremităţile a, b:
[ ] { }bxaRxba ≤≤∈=,
X(x
)](https://image.slidesharecdn.com/intervalenumerereale-150403163831-conversion-gate01/85/Intervale-numere-reale-2-320.jpg)
![Intervale mărginite
Fie a,b R∊ , a≤b şi A(a) respectiv B(b) , punctele
corespunzătoare pe axa numerică
A(a
)
‚àû‚àí ‚àû+
B(b
)
Interval semideschis cu extremităţile a, b,
( ] { }bxaRxba ≤∈= ,
deschis la stânga şi închis la dreapta:
X(x
)](https://image.slidesharecdn.com/intervalenumerereale-150403163831-conversion-gate01/85/Intervale-numere-reale-5-320.jpg)
![Intervale nemărginite
Fie a, R∊ , şi A(a) punctul corespunzător pe axa
numerică
‚àû‚àí ‚àû+
Interval inchis la dreapta şi nemărginit la
st√¢nga
( ] { }axRxa ≤∈=∞− ,
A(a
)
X(x
)](https://image.slidesharecdn.com/intervalenumerereale-150403163831-conversion-gate01/85/Intervale-numere-reale-8-320.jpg)

