ビジネス基礎講座:統計学入門 introduction to statistics
- 1. 統計学入門 ビジネスマンの基礎知識⑦ Masaaki NABESHIMA Mar 29, 2024 1 Version 1.2
- 2. ? 多くの先人により確立されたフレームワーク ? 過去の勉強会 ? テクニカルライティング ? プレゼンテーション①② ? プロジェクトマネージメント①② ? セキュリティマネージメント ? 取り扱っていない題材 ? 統計 ? マーケティング 2 ビジネスマンの基礎知識
- 3. ? データサイエンティストのツール ? データエンジニア、データサイエンティスト ? エンジニア系で最もホットな職業 ? 日々の業務への適用 ? 大企業や一流企業では普通に使われれる ? 日々の生活 ? データの正しい見方の習得(生活の精度向上) 3 はじめに:統計学
- 4. ? データサイエンティスト協会 ? DS(データサイエンティスト)検定 リテラシーレベル ? 範囲 ? データサイエンティスト(各種数学)力 ? データエンジニアリング(プログラミング?実装)力 ? ビジネス力 ? 補足 ? リテラシーレベル(入門)のみ 4 データサイエンティスト資格
- 5. ? 日本数学検定協会 ? データサイエンス数学ストラテジスト ? 中級 ? 高校1年レベルの数学一般 ? 上級 ? 大学教養レベルの数学一般 ? ディープラーニング協会 ? G検定 ? AI?ディープラーニング一般 ? E検定 ? AI?ディープラーニング詳細 5 データサイエンティスト資格
- 6. ? 統計質保証(しつほしょう)推進協会 ? 統計検定 ? 統計調査士 ? 統計調査士、専門統計調査士 ? DS(データサイエンス) ? 基礎、発展、エキスパート 6 データサイエンティスト資格 レベル 補足 1級 大学専門(3、4年) 現実的には修士レベル 準1級 2級 大学教養(1、2年) 計算問題必須 3級 高校 4級 中学
- 7. ? 統計を少しかじったアマチュアが書いた資料です ? 統計検定2級は合格 ? 大学学部は数理科学(数学専攻) ? 本資料の狙い ? 大学教養(統計検定2級)レベル ? 統計をツールとして説明 ? 公式の証明は一切なし 7 注意事項
- 8. ? 記述統計学 ? 与えられた(全)データの性質を明らかにする ? 関係性の追求 ? 例:各種マーケティング(原因追及、未来予想) ? 推測統計学 ? 少数のデータから母集団を明らかにする ? 少数データの追求(確率論の活用) ? 例:視聴率調査、選挙速報 8 統計学分類
- 9. ? 記述統計学 ? 概要 ? 与えられた(全)データの性質を明らかにする ? 手法 ? 代表値、分布、表示方法 ? 相関分析、単回帰分析、多変量解析(重回帰分析、判別分析、主成 分分析、因子分析、クラスター分析) ? ツール ? エクセル、R ? 入力:データ ? 出力:各種統計値 9 統計学分類(1)
- 10. ? 推測統計学 ? 概要 ? 少数のデータから母集団を明らかにする ? 手法 ? 推定(点推定、区間推定) ? 検定 ? ツール ? なし:作業者が統計知識をもとに作業する ? 補足:Chat GPT ? 正しい依頼文を入れれば結果がでる場合もある 10 統計学分類(2)
- 11. ? 標本の大きさと数 ? 標本数(Number of samples 、サンプル数) ? 意味 ? 実験(アンケート)の回数 ? 標本の大きさ(Sample size 、サンプルサイズ) ? 意味 ? 1回の実験(アンケート)で得られたデータ数 ? 例 ? 実験を2回行い、それぞれ5個のデータが得られた ? 標本数(サンプル数):2 ? 標本の大きさ(サンプルサイズ):5 11 補足:標本の「大きさと数」
- 12. 12 パート1:記述統計学
- 13. ? 目的:データ群の特徴を説明する ? 統計値 ? 平均、標準偏差(分散)、共分散 ? メディアン(中央値)、モード(最頻値)、歪度、突度 ? ポイント ? 平均値だけではデータ群の特徴を説明できない ? お金関連(富は上位層に偏る) ? 体験関連(悪体験のあぶり出し) ? 工業製品(平均値は固定、精度が問題) 13 記述統計学
- 14. ? お金関連(年収、貯蓄、住宅価格) ? 右に偏る ? 例:日本の貯蓄額 ? 上位2割が約6割の貯蓄を持つ ? ツール ? 度数分布表、ヒストグラム ? 中央値 ? 補足:海外メディアでは中央値が使われる事が多い ? 年収、住宅価格 14 記述統計学:平均値の罠
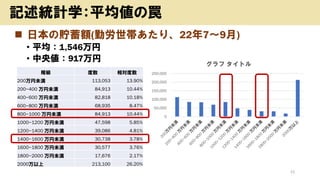
- 15. ? 日本の貯蓄額(勤労世帯あたり、22年7~9月) ? 平均:1,546万円 ? 中央値:917万円 15 記述統計学:平均値の罠 0 50,000 100,000 150,000 200,000 250,000 グラフ タイトル 階級 度数 相対度数 200万円未満 113,053 13.90% 200~400 万円未満 84,913 10.44% 400~600 万円未満 82,818 10.18% 600~800 万円未満 68,935 8.47% 800~1000 万円未満 84,913 10.44% 1000~1200 万円未満 47,598 5.85% 1200~1400 万円未満 39,086 4.81% 1400~1600 万円未満 30,738 3.78% 1600~1800 万円未満 30,577 3.76% 1800~2000 万円未満 17,676 2.17% 2000万以上 213,100 26.20%
- 16. ? 補足:パレートの法則(2?8の法則) ? 上位2割が全体の8割を占める ? 平均値の議論では本質的な正解は得られない ? もう一段踏み込んだ議論が必須 ? (例)売上:上位2割の(顧客or商品or要因)が売り上げの8割に影響する ? 上位2割(顧客or商品or要因)のあぶり出し?対策 ? 顧客?商品分析:デシル、RFM、CPM分析 ? 要因分析:多変量解析 ? 補足:ロングテール(ネット販売の強み) ? 店頭販売:上位2割しか扱えない ? ネット販売:あまり売れない8割も扱える 16 記述統計学:平均値の罠
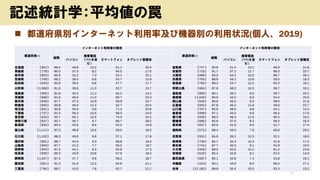
- 17. ? 都道府県別インターネット利用率及び機器別の利用状況(個人、2019) 17 記述統計学:平均値の罠 都道府県(n) インターネット利用者の割合 都道府県(n) インターネット利用者の割合 総数 総数 パソコン 携帯電話 (PHSを含 む) スマートフォン タブレット型端末 パソコン 携帯電話 (PHSを含 む) スマートフォン タブレット型端末 北海道 (661) 88.4 48.8 10.2 61.1 20.4 滋賀県 (747) 90.8 51.4 13.1 66.9 21.8 青森県 (778) 80.0 37.0 8.2 45.5 17.0 京都府 (733) 91.7 57.2 11.7 68.3 25.7 岩手県 (803) 85.9 32.2 7.0 52.1 15.1 大阪府 (669) 93.3 54.2 15.0 66.7 28.1 宮城県 (769) 86.2 38.4 9.8 54.7 15.9 兵庫県 (793) 88.8 49.1 10.6 59.5 19.3 秋田県 (933) 82.8 39.5 8.8 47.7 17.7 奈良県 (760) 89.3 54.7 12.2 65.3 19.1 山形県 (1,068) 81.0 39.6 11.0 52.7 13.7 和歌山県 (664) 87.6 48.2 10.0 56.7 19.1 福島県 (900) 81.8 40.3 11.2 54.4 14.2 鳥取県 (860) 86.1 46.2 9.0 59.7 20.2 茨城県 (696) 91.6 49.4 11.0 60.7 22.3 島根県 (1,049) 84.9 42.5 8.3 54.4 20.5 栃木県 (849) 87.7 47.3 10.9 58.9 23.7 岡山県 (816) 90.6 45.4 9.2 58.0 21.9 群馬県 (850) 90.8 49.4 12.3 62.7 20.5 広島県 (820) 87.8 46.2 11.9 59.6 22.7 埼玉県 (691) 90.8 54.9 9.8 71.4 25.8 山口県 (767) 84.9 36.6 8.8 54.1 14.3 千葉県 (727) 91.5 59.3 10.9 68.3 24.6 徳島県 (698) 87.1 43.5 9.9 56.4 17.6 東京都 (622) 95.7 65.1 10.4 74.5 33.2 香川県 (926) 88.3 48.3 11.5 60.5 19.2 神奈川県 (627) 92.7 56.7 9.7 68.7 28.2 愛媛県 (696) 84.9 37.5 8.2 58.4 16.3 新潟県 (935) 84.0 40.6 8.9 52.5 14.8 高知県 (627) 85.6 41.9 9.0 51.7 17.4 富山県 (1,111) 87.0 48.8 10.6 59.0 19.5 福岡県 (572) 88.4 49.0 7.9 65.6 25.0 石川県 (1,105) 88.3 46.6 9.8 57.1 17.8 佐賀県 (931) 84.6 39.1 10.3 52.1 18.0 福井県 (891) 88.7 44.4 9.0 58.8 19.4 長崎県 (706) 84.7 34.4 10.3 51.8 17.4 山梨県 (906) 87.7 41.2 7.7 59.2 18.7 熊本県 (744) 87.7 40.3 9.1 54.9 19.0 長野県 (945) 87.2 44.1 9.3 55.6 17.3 大分県 (659) 89.0 42.6 10.1 61.4 23.9 岐阜県 (959) 85.3 43.6 10.8 57.9 18.4 宮崎県 (616) 85.4 32.8 8.1 53.4 14.9 静岡県 (1,047) 87.4 47.7 9.9 58.2 18.7 鹿児島県 (587) 85.1 34.9 7.4 53.8 19.1 愛知県 (651) 91.3 51.5 12.3 64.6 21.1 沖縄県 (424) 90.1 43.9 8.0 66.4 27.1 三重県 (794) 89.7 43.0 7.8 62.7 21.7 全体 (37,182) 89.8 50.4 10.5 63.3 23.2
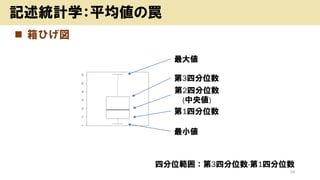
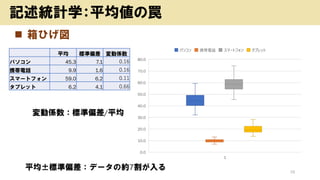
- 19. ? 箱ひげ図 19 記述統計学:平均値の罠 平均±標準偏差:データの約7割が入る 平均 標準偏差 変動係数 パソコン 45.3 7.1 0.16 携帯電話 9.9 1.6 0.16 スマートフォン 59.0 6.2 0.11 タブレット 6.2 4.1 0.66 変動係数:標準偏差/平均
- 20. ? 体験(QoE)の結果 ? データ ? 顧客アンケート、動画視聴QoE(主にバッファリング関連) ? 目的 ? 全体的な品質向上?平均値 ? 解約(チャーン)対策?悪体験の比率?あぶり出し ? ツール ? ヒストグラム、度数分布表 20 記述統計学:平均値の罠
- 21. ? OTTライブ(平均セッション長:約10分) ? 平均再バッファリング回数 ? 固定:0.27回 ? モバイル:0.36回 ? 度数分布表 ? フラストレーション(再バッファリング4回以上)セッションの割合 ? 固定:1.09% ? モバイル:2.16% 21 記述統計学:平均値の罠 0回 1回 2~3回 4~7回 8回以上 固定 91.21 5.49 2.2 0.75 0.34 モバイル 82.84 9.73 5.27 1.73 0.43
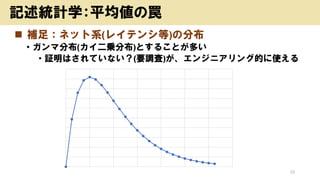
- 22. ? 補足:ネット系(レイテンシ等)の分布 ? ガンマ分布(カイ二乗分布)とすることが多い ? 証明はされていない?(要調査)が、エンジニアリング的に使える 22 記述統計学:平均値の罠
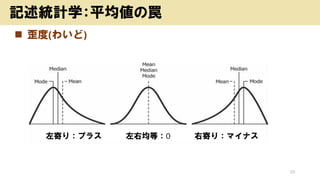
- 23. ? 歪度(わいど) 23 記述統計学:平均値の罠 左寄り:プラス 左右均等:0 右寄り:マイナス
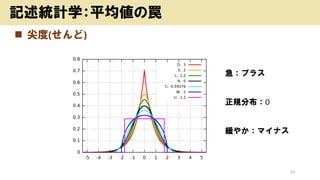
- 25. ? 工業製品 ? 平均値:いまどき平均値が大きくずれる製品はない ? 分散:微妙な誤差(偏差)がどれだけ少ないかが鍵 ? ツール ? 標準偏差 ? データ群のズレ(偏差)の大きさ ? 計算式 ? 偏差:(データ-平均) ? 分散: σ((データ?平均)2) データの個数 ? 標準偏差: 分散 25 記述統計学:平均値の罠
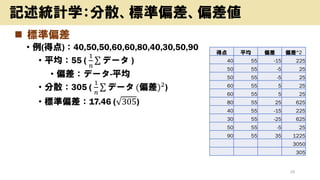
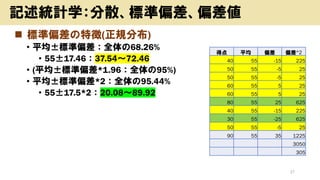
- 26. ? 標準偏差 ? 例(得点):40,50,50,60,60,80,40,30,50,90 ? 平均:55 ( 1 ? σ データ ) ? 偏差:データ-平均 ? 分散:305 ( 1 ? σ データ (偏差)2 ) ? 標準偏差:17.46 ( 305) 26 記述統計学:分散、標準偏差、偏差値 得点 平均 偏差 偏差^2 40 55 -15 225 50 55 -5 25 50 55 -5 25 60 55 5 25 60 55 5 25 80 55 25 625 40 55 -15 225 30 55 -25 625 50 55 -5 25 90 55 35 1225 3050 305
- 27. ? 標準偏差の特徴(正規分布) ? 平均±標準偏差:全体の68.26% ? 55±17.46:37.54~72.46 ? (平均±標準偏差*1.96:全体の95%) ? 平均±標準偏差*2:全体の95.44% ? 55±17.5*2:20.08~89.92 27 記述統計学:分散、標準偏差、偏差値 得点 平均 偏差 偏差^2 40 55 -15 225 50 55 -5 25 50 55 -5 25 60 55 5 25 60 55 5 25 80 55 25 625 40 55 -15 225 30 55 -25 625 50 55 -5 25 90 55 35 1225 3050 305
- 28. ? 偏差値 ? 標準偏差により得点のポジションを示したもの ? 偏差値: 得点-平均点 標準偏差 *10+50 ? 見方 ? 70:上位約2.5% ? 60:上位約15% ? 50:中央 ? 40:下位約15% ? 30:下位約2.5% 28 記述統計学:分散、標準偏差、偏差値 得点 平均点 偏差値 40 55 41 50 55 47 50 55 47 60 55 53 60 55 53 80 55 64 40 55 41 30 55 36 50 55 47 90 55 70
- 29. ? 日本人女性(成人)の身長 ? 平均:157.5cm ? 標準偏差:5.4cm ? 日本人女性?花子さん(成人)の身長を区間推定 ? 信頼度:68.26% ? 157.5±標準偏差 ? 157.5±5.4cm ? 152.1cm~162.9cm ? 信頼度:95% ? 157.5±1.96*標準偏差 ? 157.5±1.96*5.4cm ? 146.9cm~約168.1cm 29 標準偏差からの予測(予測統計学) 「予測の信頼度」を上げる ?「区間推定の範囲」を広げる
- 30. ? 「予測の信頼度」と「区間推定の範囲」 ? 予測の信頼度を上げる ? 区間推定の範囲を広げる(予測を当たりやすくする) ? 95%の信頼度 ? まれな事(5%)が無い限り正しい 30 標準偏差からの予測(予測統計学) 予測の信頼度 範囲 68.26% ±標準偏差 152.1 ~ 162.9 95.44% ±2*標準偏差 146.9 ~ 168.1
- 31. ? 入力 ? 日本人女性(成人)の平均身長が157.5cm、標準偏差5.4cmである場合、日 本人女性(成人)Aさんの身長を95%で予測するとどの範囲になる? ? 回答 ? 日本人女性(成人)の平均身長が157.5cm、標準偏差が5.4cmの正規分布を 仮定します。95%の信頼区間を求めるために、以下の計算を行います。 ? 95%の信頼区間は、平均から左右に標準偏差の1.96倍を考慮した範囲にな ります。標準偏差が5.4cmなので、1.96倍すると約10.584cmになります。 ? したがって、日本人女性(成人)Aさんの身長を95%の確率で予測すると、 平均身長から10.584cmを上下に足し引いた範囲になります。 ? 157.5±1.96×5.4157.5±1.96×5.4 ? 157.5±10.584157.5±10.584 ? したがって、日本人女性(成人)Aさんの身長を95%の確率で予測すると、 約146.916cmから約168.084cmの間になります。 31 標準偏差からの予測(例ChatGPT)
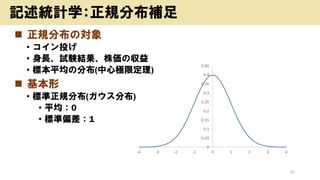
- 32. ? 正規分布の対象 ? コイン投げ ? 身長、試験結果、株価の収益 ? 標本平均の分布(中心極限定理) ? 基本形 ? 標準正規分布(ガウス分布) ? 平均:0 ? 標準偏差:1 32 記述統計学:正規分布補足 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 -4 -3 -2 -1 0 1 2 3 4
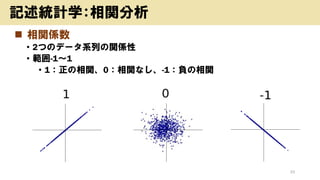
- 33. ? 相関係数 ? 2つのデータ系列の関係性 ? 範囲-1~1 ? 1:正の相関、0:相関なし、-1:負の相関 33 記述統計学:相関分析
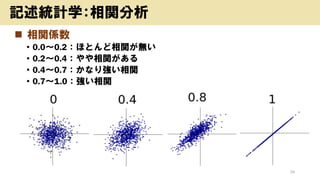
- 34. ? 相関係数 ? 0.0~0.2:ほとんど相関が無い ? 0.2~0.4:やや相関がある ? 0.4~0.7:かなり強い相関 ? 0.7~1.0:強い相関 34 記述統計学:相関分析
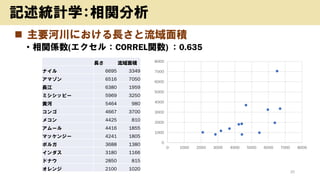
- 35. ? 主要河川における長さと流域面積 ? 相関係数(エクセル:CORREL関数) :0.635 35 記述統計学:相関分析 長さ 流域面積 ナイル 6695 3349 アマゾン 6516 7050 長江 6380 1959 ミシシッピー 5969 3250 黄河 5464 980 コンゴ 4667 3700 メコン 4425 810 アムール 4416 1855 マッケンジー 4241 1805 ポルガ 3688 1380 インダス 3180 1166 ドナウ 2850 815 オレンジ 2100 1020 0 1000 2000 3000 4000 5000 6000 7000 8000 0 1000 2000 3000 4000 5000 6000 7000 8000
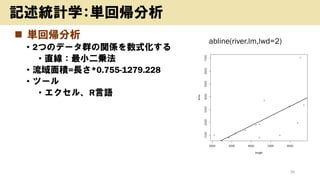
- 36. ? 単回帰分析 ? 2つのデータ群の関係を数式化する ? 直線:最小二乗法 ? 流域面積=長さ*0.755-1279.228 ? ツール ? エクセル、R言語 36 記述統計学:単回帰分析 abline(river.lm,lwd=2)
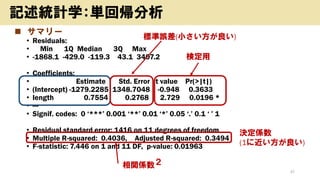
- 37. ? サマリー ? Residuals: ? Min 1Q Median 3Q Max ? -1868.1 -429.0 -119.3 43.1 3407.2 ? Coefficients: ? Estimate Std. Error t value Pr(>|t|) ? (Intercept) -1279.2285 1348.7048 -0.948 0.3633 ? length 0.7554 0.2768 2.729 0.0196 * ? --- ? Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ? Residual standard error: 1416 on 11 degrees of freedom ? Multiple R-squared: 0.4036, Adjusted R-squared: 0.3494 ? F-statistic: 7.446 on 1 and 11 DF, p-value: 0.01963 37 記述統計学:単回帰分析 標準誤差(小さい方が良い) 決定係数 (1に近い方が良い) 相関係数2 検定用
- 38. ? R言語による実行 ? river <- read.csv("/tmp/rever.csv",header=TRUE) ? ファイル読み込み ? river.lm <- lm(area~length, data=river) ? 回帰分析実行 ? abline(river.lm,lwd=2) ? グラフ描画 ? summary(river.lm) ? サマリー出力 38 記述統計学:単回帰分析 length area 6695 3349 6516 7050 6380 1959 5969 3250 5464 980 4667 3700 4425 810 4416 1855 4241 1805 3688 1380 3180 1166 2850 815 2100 1020 rever.csv
- 39. ? 多変量解析 ? 複数の要因?成分の解析 ? 本格的なマーケティング分析 ? 手法 ? 重回帰分析、判別分析、主成分分析、因子分析、クラスター分析 ? レベル ? 統計検定準1級 (ごめんなさい、今回は扱いません) 39 記述統計学:多変量解析
- 40. 40 パート2:予測統計学
- 41. ? 標本と母集団の予測、標本の大きさ ? 予測 ? 母比率(母集団における比率) ? 母平均(母集団の平均) ? 母分散(母集団の分散) ? 標本の大きさ ? 必要な精度を満たす(最小の)「標本の大きさ」 41 予測統計学 母集団 標本
- 42. ? 対象 ? 単体(例:母平均) ? 差 (例:「2つの母平均」の差) ? 比率 (例:「2つの母平均」の比率) ? 算出条件 ? 標本の大きさ:大標本or 小標本 ? 母集団の大きさ:無限 or not ? 母集団の分布:正規分布 or not ? 母分散:既知 or not ? 検定 ? 片側(以上 or 以下) ? 両側(= or ≠) 42 予測統計学 予測統計学の難しさ ?算出方法が莫大:単純計算で288通り (3*3*2*2*2*2*2)
- 43. ? 本資料で説明するサンプル ? 母比率(単体)/(大標本) ? 区間推定 ? 標本の大きさ ? 検定(両側) ? 母平均(単体)/(小標本、母集団:正規分布、母分散:未知) ? 検定(片側) 43 予測統計学
- 44. ? 母比率の信頼区間 ? 用途 ? 比率に関する調査(内閣支持率、視聴率、選挙結果等)の結果に対す る区間推定 ? 公式(大標本) ? 標本数:n ? 比率:p ? 95%信頼区間 ? ? ± 1.96 × ?(1??) ? 44 予測統計学:母比率(区間推定) 母平均の標準誤差
- 45. ? 内閣支持率のアンケート:支持率20% ? 100人に実施 ? 支持率の95%信頼区間幅 ? ? ± 1.96 × 0.8(1?0.8) 100 ? ? ± 1.96 × 0.16 100 ? ? ± 0.0784 ? 12.16 ~ 27.84 (幅:15.7%) ? 1000人に実施 ? 支持率の95%信頼区間 ? ? ± 1.96 × 0.8(1?0.8) 1000 ? ? ± 1.96 × 0.16 1000 ? ? ± 0.0248 ? 17.53 ~ 22.47 (幅:5.0%) 45 予測統計学:母比率(区間推定)
- 46. ? ChatGPT ? 問 ? 内閣支持率のアンケートを行ったところ、支持率が20%であった、 アンケート数が1000人だとして95%の信頼区間をもとめよ ? 回答 ? 95%の信頼区間を求めるには、通常、以下のステップを実行しま す: ? <省略> ? したがって、95%の信頼水準で、内閣の支持率の推定値は約17.53% から約22.47%の間にあります。 46 予測統計学:母比率(区間推定)
- 47. ? 必要な標本の大きさ(回答数) ? 内閣支持率のアンケートを行うにあたり、信頼区間が3%以下となる回 答数nを求めよ(支持率の前提は無いものとする) ? 2 ? 1.96 × ?(1??) ? < 0.03?1.96 × ?(1??) ? < 0.015 ? ? 1?? ? < 0.015 1.96 ? ?(1??) ? < 0.0152 1.962 ? 1.962 0.0152 ?(1 ? ?) < ? ? 17074 ? ? 1 ? ? < ? ? 17074 ? 0.5 1 ? 0.5 < ? ? 4268.4 < ? ? n=4269 47 予測統計学:母比率(必要な標本の大きさ) p(1-p)の最大値 0.5*0.5=0.25 0.2*0.8=0.16 0.1*0.9=0.09
- 48. ? ChatGPT ? 問 ? 内閣支持率のアンケートを行う、信頼区間を3%にするには何人の アンケートが必要か? ? 回答 ? 信頼区間を3%にするために必要なアンケートのサンプルサイズを 求めるには、以下の手順に従います。 ? <省略> ? したがって、信頼区間を3%にするためには、約4269人のアンケー トが必要です。 48 予測統計学:母比率(必要な標本の大きさ)
- 49. ? アプローチ 1. 帰無仮説を作成 2. 帰無仮説に対する検定統計量を計算 3. 検定統計量がその分布の95%の内側にあるか判定 ? 外側:帰無仮説を棄却 ? その仮説が起こることは5%未満(まれ)である ? 内側:帰無仮説を棄却できない ? その仮説が起こることは5%以上である 49 予測統計学:検定
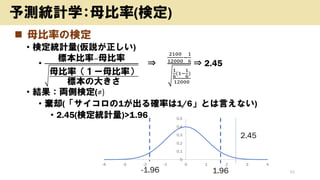
- 50. ? 母比率の検定 ? さいころの正確性 ? さいころを12,000投げると1が2,100回出た、歪んでいるか有意水 準5%で検定せよ ? 帰無仮説 ? サイコロの1が出る確率は1/6 ? 検定統計量 ? 標本比率?母比率 母比率(1ー母比率) 標本の大きさ ? 分布:標準正規分布 50 予測統計学:母比率(検定)
- 51. ? 母比率の検定 ? 検定統計量(仮説が正しい) ? 標本比率?母比率 母比率(1ー母比率) 標本の大きさ ? 2100 12000 ? 1 6 1 6(1? 1 6) 12000 ? 2.45 ? 結果:両側検定(≠) ? 棄却(「サイコロの1が出る確率は1/6」とは言えない) ? 2.45(検定統計量)>1.96 51 予測統計学:母比率(検定) 0 0.1 0.2 0.3 0.4 0.5 -4 -3 -2 -1 0 1 2 3 4 1.96 2.45 -1.96
- 52. ? 母比率の検定 ? 棄却:2.45(検定統計量)>1.96 ? 意味 ? 2.45:この仮説が成り立つのは100回に0.7回 ? 1.96:この仮説が成り立つのは100回に2.5回 52 予測統計学:母比率(検定) 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.500 0.496 0.492 0.488 0.484 0.480 0.476 0.472 0.468 0.464 0.1 0.460 0.456 0.452 0.448 0.444 0.440 0.436 0.433 0.429 0.425 1.8 0.036 0.035 0.034 0.034 0.033 0.032 0.031 0.031 0.030 0.029 1.9 0.029 0.028 0.027 0.027 0.026 0.026 0.025 0.024 0.024 0.023 2.0 0.023 0.022 0.022 0.021 0.021 0.020 0.020 0.019 0.019 0.018 2.3 0.011 0.010 0.010 0.010 0.010 0.009 0.009 0.009 0.009 0.008 2.4 0.008 0.008 0.008 0.008 0.007 0.007 0.007 0.007 0.007 0.006 2.5 0.006 0.006 0.006 0.006 0.006 0.005 0.005 0.005 0.005 0.005 標準正規分布表 横軸上位 横軸下位 上側確率
- 53. ? ChatGPT ? 問 ? さいころを12,000投げると1が2,100回出た、標本の大きさが十分に 大きいとして、歪んでいるか有意水準5%で検定せよ ? 回答 ? この問題では、標本の大きさが十分に大きいため、中心極限定理 により、標本分布が近似的に正規分布に従うと仮定できます。そ のため、母集団のパラメータを推定するための検定には、z検定を 使用します。 ? <省略> ? したがって、結論として、さいころは有意水準5%で歪んでいると 結論付けることができます。 53 予測統計学:母比率(検定)
- 54. ? 母平均(小標本、母集団:正規分布) ? 不偏分散=標本分散*n/(n-1) ? 標本の分散は小さくなりがちなので補正する ? 検定統計量 ? 標本平均ー母平均 不偏分散 標本の大きさ ? t分布(自由度:標本の大きさ―1) 54 予測統計学:母平均
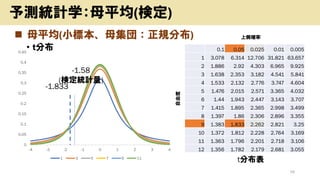
- 55. ? 母平均(小標本、母集団:正規分布) ? 前提 ? 製品10個の寿命:1,950時間 ? 母分散:未知 ? 不偏分散:(100時間)^2 ? 仮定: ? 製品の平均寿命:2,000時間 ? 検定統計量 ? 標本平均ー母平均 不偏分散 標本の大きさ ? 1950 ?2000 100?100 10 ? -1.58 ? t分布(自由度:標本の大きさ―1) ? 片側検定(寿命が短い場合のみが問題) 55 予測統計学:母平均(検定)
- 56. ? 母平均(小標本、母集団:正規分布) ? t分布 56 予測統計学:母平均(検定) 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 -4 -3 -2 -1 0 1 2 3 4 1 3 5 7 9 11 0.1 0.05 0.025 0.01 0.005 1 3.078 6.314 12.706 31.821 63.657 2 1.886 2.92 4.303 6.965 9.925 3 1.638 2.353 3.182 4.541 5.841 4 1.533 2.132 2.776 3.747 4.604 5 1.476 2.015 2.571 3.365 4.032 6 1.44 1.943 2.447 3.143 3.707 7 1.415 1.895 2.365 2.998 3.499 8 1.397 1.86 2.306 2.896 3.355 9 1.383 1.833 2.262 2.821 3.25 10 1.372 1.812 2.228 2.764 3.169 11 1.363 1.796 2.201 2.718 3.106 12 1.356 1.782 2.179 2.681 3.055 -1.833 -1.58 (検定統計量) t分布表 自由度 上側確率
- 57. ? 母平均(小標本、母集団:正規分布) ? 検定結果: ? 棄却されない ? 「平均寿命が2,000時間」であることを否定できない ? -1.833<-1.58(検定統計量)の意味 ? -1.58:この仮説が成り立つのは100回に5回よりは大きい ? -1.833:この仮説が成り立つのは100回に5回 57 予測統計学:母平均(検定) 0.1 0.05 0.025 0.01 0.005 9 1.383 1.833 2.262 2.821 3.25
- 58. ? ChatGPT ? 問 ? 製品10個の寿命を調べたら、平均1950時間かつ不偏分散が10000で あった、母分散が未知として、製品の平均寿命が2000時間であるか、 95%で検定せよ ? 回答 ? この問題では、母集団の平均寿命が2000時間であるかどうかを検定し ます。 ? <省略> ? 帰無仮説 (H?): 製品の平均寿命は2000時間である。 ? <省略> ? 帰無仮説を棄却できません。したがって、この検定では、製品の平均 寿命が2000時間であるという主張を支持する証拠は見つかりません。 58 予測統計学:母平均(検定) ない 間違い
- 59. ? 統計 ? 勉強する価値あり ? 日々の生活:いろいろなデータの正しい見方 ? 日々の業務:業績アップ ? データサイエンティスト:高給与への道 ? 勉強のゴール付け ? 統計検定がお勧め 59 おわりに
- 60. ? 統計検定3級 ? レベル:高校 ? 必要な統計の公式:数個 ? 必要な勉強時間:1週間 ? 統計検定2級 ? レベル:大学教養 ? 必要な統計の公式:20~30個ぐらい ? 必要な勉強時間:1か月 ? 注意点:過去問主体の勉強 ? 公式教科書:難しい(ほぼ統計の教科書そのまま) ? 公式問題集:解説が分かりにくい(ネットをあさる必要あり) ? 過去問 ? https://www.toukei-kentei.jp/prepare/kakomon/ 60 補足:統計検定のレベル