More Related Content Similar to K030 appstat201203 2variable (20)
搁によるデータサイエンス:12章「时系列」 搁によるデータサイエンス:12章「时系列」
Nagi Teramo ?
書籍:Rによるデータサイエンス(http://www.amazon.co.jp/dp/4627096011)の12章「時系列」の内容に沿った資料です。
第17回R勉強会@東京(#TokyoR)(http://atnd.org/events/19835)に使用。
More from t2tarumi (14)
K050 t分布f分布 K050 t分布f分布
t2tarumi ?
The document discusses the t distribution and F distribution. It provides graphs of their probability density functions and examples of simulating random values from each distribution. It also shows how to calculate a t-statistic and F-ratio from sample data and compares the results to the theoretical distributions.
1. 1
情報統計学
2 変量データの分析
20110520 scale 修正
20120502 スライド追加(散布図)
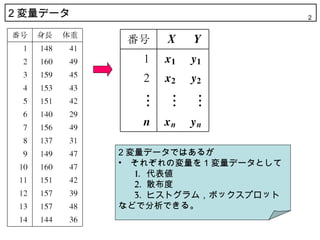
2. 2 変量データ 2
2 変量データではあるが
? それぞれの変量を 1 変量データとして
1. 代表値
2. 散布度
3. ヒストグラム,ボックスプロット
などで分析できる。
3. データの登録 3
データを登録,読み込む方法
? weight という名前で登録し,その後, bodydata という形でま
とめる。
? bodydata として行列で登録
4. ファイルからデータを読み込む(重要) 4
? data1.txt というデータファイルがあるとする。スペース or タ
ブ区切り。
? data1.csv という CSV ファイルを読み込むには
? data1-1.csv という CSV ファイ
? データを確認してみよう ルbodydata <-read.csv("data1-1.csv")
>
5. データの一部を取り出す 5
? まず, 1 変量ずつ分析するため,一部を取り出そう
? height, weight それぞれについて一変量の分析を行う。
? 関数 one.var.analysis をつくってあるのでそれを使う。
7. 2 変量の分析 7
? 并行箱ひげ図
> boxplot(height, weight, names=c(”height”, ”weight”))
ちなみに
> boxplot(as.vector(scale(height)), as.vector(scale(weight)), names=c(“height”, “weight”))
とすれば ???
単位の異なる変数、
数値の桁が異なる変数
の平行箱ひげ図は
意味が無い!ことが多い
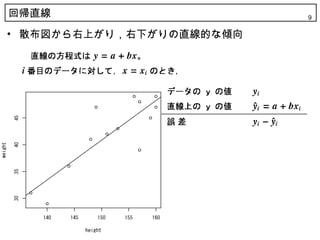
9. 回帰直线 9
? 散布図から右上がり,右下がりの直線的な傾向
14. 共分散?相関係数 14
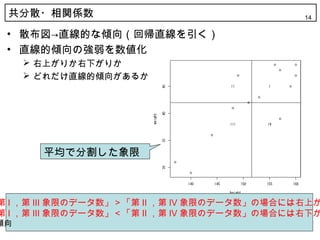
? 散布図→直線的な傾向(回帰直线を引く)
? 直線的傾向の強弱を数値化
? 右上がりか右下がりか
? どれだけ直線的傾向があるか
平均で分割した象限
第 I ,第 III 象限のデータ数」>「第 II ,第 IV 象限のデータ数」の場合には右上が
第 I ,第 III 象限のデータ数」<「第 II ,第 IV 象限のデータ数」の場合には右下が
傾向
15. 15
? 「第 I ,第 III 象限のデータ数」 - 「第 II ,第 IV 象限のデー
タ数」
? 正の場合は右上がり
? 負の場合は右下がり
? 最大の値は n – 0 = n
? 最小の値は 0 – n = – n
2 つのデータでデータサイズが異なると (nA と nB など),値により比較が
しにくい。
? 比較しやすいようにデータ数で割る
範囲は,-1から1
± 1に近いほど傾向が強い
? ケンドール
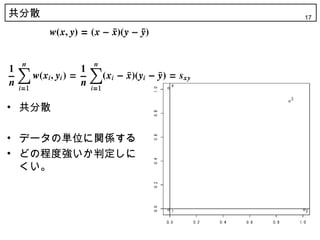
17. 共分散 17
? 共分散
? データの単位に関係する
? どの程度強いか判定しに
くい。
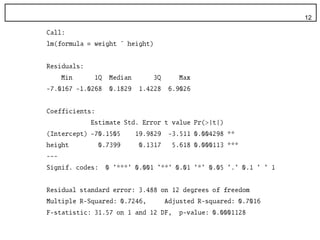
19. R における共分散,相関係数 19
? R で共分散を計算するには
? cov を使う
cov(height, weight)
? var でも計算できる
? n-1 で割っていることを確認すること。 P 37
? R で相関係数を計算
? cor を使う
? cor(height, weight)
? この例では, 0.851212
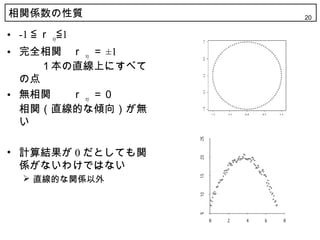
20. 相関係数の性质 20
? -1 ≦ r xy≦1
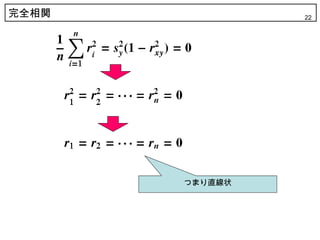
? 完全相関 r xy = ±1
1本の直線上にすべて
の点
? 無相関 r xy =0
相関(直線的な傾向)が無
い
? 計算結果が 0 だとしても関
係がないわけではない
? 直線的な関係以外
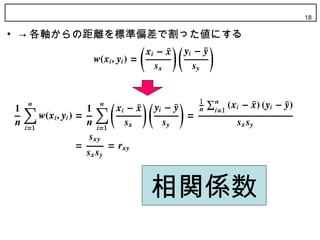
23. 散布図と相関係数 23
? 散布図を見て,相関係数の値を読み取れるように練習。
? testcor()
? 誤差は ±0.1 の範囲で。
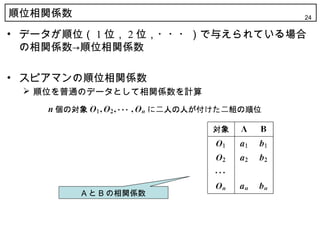
24. 顺位相関係数 24
? データが順位( 1 位, 2 位,???)で与えられている場合
の相関係数→顺位相関係数
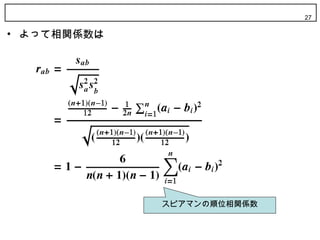
? スピアマンの顺位相関係数
? 順位を普通のデータとして相関係数を計算
A と B の相関係数
28. ケンドールの顺位相関係数 28
? 順位を全部に対してつけるのは難しい。
? 順位をつけられない場合もある
? n 個の対象から取り出した nC2 組の 2 つの組み合わせに対して
大小関係をつける。
? A,B の 2 名に大小関係をつけてもらう
? 一致した組数 K
? 不一致の組数 L
? M=K+L
? このとき ケンドールの順位相関係
数
30. 多変量データのグラフ表现 30
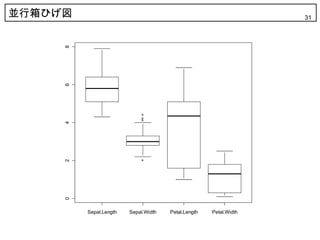
? iris データ
? 3 種類のアイリス(アヤメ)について各 50 個の花を, 4 ヶ所ずつ測定
したデータ
? がくの長さ
? がくの幅
? 花弁の長さ
? 花弁の幅
? 有名なデータで,統計の分野では,よく利用される。
? iris で確認できる。
31. 并行箱ひげ図 31
8
6
4
2
0
Sepal.Length Sepal.Width Petal.Length Petal.Width
32. 散布図行列 32
? pairs(iris[1:4])
? pairs(iris[1:4],pch=21,bg = c("red", "green3", "blue")[unclass(iris$Species)])
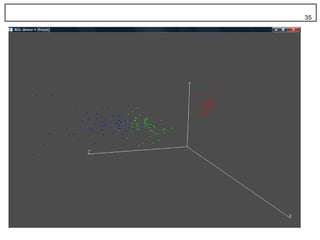
33. 3 次元散布図 33
library(rgl)
rgl.points(iris[1:50,1], iris[1:50,2], iris[1:50,3], color="red", size=3)
rgl.points(iris[51:100,1], iris[51:100,2], iris[51:100,3], color="green",
size=3)
rgl.points(iris[101:150,1], iris[101:150,2], iris[101:150,3],
color="blue", size=3)
rgl.lines(c(0, max(iris[, 1])), c(0, 0), c(0, 0))
rgl.lines(c(0, 0), c(0, max(iris[, 2])), c(0, 0))
rgl.lines(c(0, 0), c(0, 0), c(0, max(iris[, 3])))
text3d(max(iris[, 1]), 0, 0, text = "X")
text3d(0, max(iris[, 2]), 0, text = "Y")
text3d(0, 0, max(iris[, 3]), text = "Z")
34. パッケージのインストール
? > library(rgl)
以下にエラー library(rgl) : 'rgl' という名前のパッケージはあ
りません
? パッケージ「 rgl 」がインストールされていない。
? Rgui ウィンドウのメニュー「パッケージ」より
? CRAN ミラーサイトの設定
? Japan(Aizu) を選択(日本のどこでも可)
? パッケージのインストール
? rgl を選択
36. 平行座标プロット 36
library(MASS)
parcoord(iris[1:4], col = 1 + (0:149)%/%50)
37. 散布図と相関係数 37
? 散布図を見て,相関係数の値を読み取れるように練習。
? testcor()
? 誤差は ±0.1 の範囲で。



















![散布図行列 32
? pairs(iris[1:4])
? pairs(iris[1:4],pch=21,bg = c("red", "green3", "blue")[unclass(iris$Species)])](https://image.slidesharecdn.com/k030appstat201203-2variable-130416203037-phpapp01/85/K030-appstat201203-2variable-32-320.jpg)
![3 次元散布図 33
library(rgl)
rgl.points(iris[1:50,1], iris[1:50,2], iris[1:50,3], color="red", size=3)
rgl.points(iris[51:100,1], iris[51:100,2], iris[51:100,3], color="green",
size=3)
rgl.points(iris[101:150,1], iris[101:150,2], iris[101:150,3],
color="blue", size=3)
rgl.lines(c(0, max(iris[, 1])), c(0, 0), c(0, 0))
rgl.lines(c(0, 0), c(0, max(iris[, 2])), c(0, 0))
rgl.lines(c(0, 0), c(0, 0), c(0, max(iris[, 3])))
text3d(max(iris[, 1]), 0, 0, text = "X")
text3d(0, max(iris[, 2]), 0, text = "Y")
text3d(0, 0, max(iris[, 3]), text = "Z")](https://image.slidesharecdn.com/k030appstat201203-2variable-130416203037-phpapp01/85/K030-appstat201203-2variable-33-320.jpg)

![平行座标プロット 36
library(MASS)
parcoord(iris[1:4], col = 1 + (0:149)%/%50)](https://image.slidesharecdn.com/k030appstat201203-2variable-130416203037-phpapp01/85/K030-appstat201203-2variable-36-320.jpg)
