JOIss2015-ZDD @bekasa001
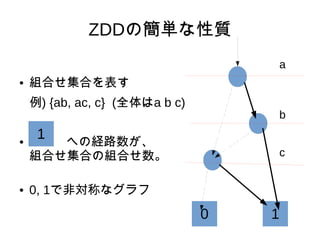
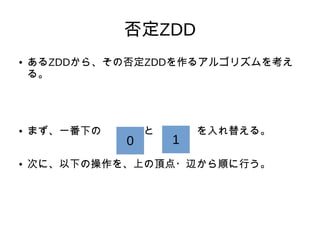
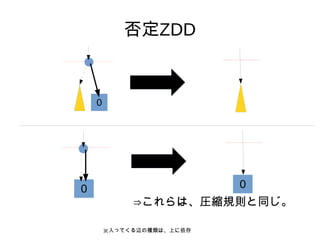
- 2. ZDD§Œ∫ÜÖg§ –‘Ÿ| °Ò ΩM∫œ§ªºØ∫œ§Ú±Ì§π ¿˝) {ab, ac, c} (»´Ã§œa b c) °Ò °°§ÿ§ŒΩU¬∑ ˝§¨°¢ ΩM∫œ§ªºØ∫œ§ŒΩM∫œ§ª ˝°£ °Ò 0, 1§«∑«åù≥∆§ •∞•È•’ 0 1 a b c 1
- 3. åg◊∞§Œ∏≈“™ °Ò §‚°¢◊”§Ú≥÷§ø§ §§•Œ©`•…§»§∑§∆íQ§¶°£ °Ò ∏˜•Œ©`•…§œ 1- fix§Œœ»§Œ•›•§•Û•ø 0- fix§Œœ»§Œ•›•§•Û•ø 1- fix§«Ω”æA§µ§Ï§ø”H§Œ•›•§•Û•ø§ŒºØ∫œ(std::set) 0- fix§«Ω”æA§µ§Ï§ø”H§Œ•›•§•Û•ø§ŒºØ∫œ(std::set) §Ú≥÷§ƒ°£ °Ò 1§ƒ§Œ•∞•È•’§œ°¢“ª∑¨…œ§ŒÌ§ÿ§Œ•›•§•Û•ø§«±Ì ¨F§µ§Ï§Î°£ 0 1
- 4. °Ò °∏0, 1§«∑«åù≥∆§ •∞•È•’°π ? °∏0§»1§Ú»Î§ÏÃʧ®§ø§È√Ê∞◊§§§´§‚§∑§Ï§ §§°π °°°°°°°°§»øº§®§ø°£ ∞kœÎ
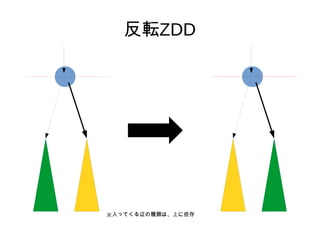
- 5. °Ò —} ˝§Œ§‚§Œ§Úflx§÷ΩM§fl∫œ§Ô§ª§ŒºØ∫œ§Ú±Ì§πZDD§´§È°¢ flx§–§ §§§‚§Œ§Úflx§÷ΩM§fl∫œ§Ô§ª§ŒºØ∫œ§Ú±Ì§πZDD§Ú ◊˜§√§∆§fl§Î°£ ¿˝) »´ÃÂ§Ú a, b, c §»§∑§∆°¢ §‚§»§ŒºØ∫œ§¨{ab, ac, c}§Œ§»§≠§Œ{c, b, ab} ?§≥§Ï§Ú°∏∑¥‹ûZDD°π§»∫Ù§÷§≥§»§À§π§Î°£ ∑¥‹ûZDD
- 10. ∑¥‹ûZDD °Ò §≥§Ï§È§Œ◊˜òI§Ú°¢…œ§ŒÌ?fix§´§ÈÌò§À––§¶§» …œ ÷§Ø§§§√§ø°£ °Ò §≥§Ï§È§Œ§≥§»§Ú––§√§ø§¿§±§«§œ°¢–¬§ø§ µ»Å˝Ω” µ„§¨…˙§fi§Ï§Îø…ƒ‹–‘§¨§¢§Í°¢º»ºsZDD§œµ√§È§Ï § §§°£ °Ò ”ãÀ„¡ø§œ°¢O(V * N)§Ø§È§§?(N§œ“™Àÿ ˝)
- 11. ∑Ò∂®ZDD °Ò §¢§ÎΩM§fl∫œ§Ô§ªºØ∫œ§Ú±Ì§πZDD§´§È°¢§Ω§≥§«§’§µ§Ô §∑§Ø§ §§§»§µ§Ï§ÎΩM§fl∫œ§Ô§ª§ŒºØ∫œ§Ú±Ì§πZDD§Ú ◊˜§√§∆§fl§Î°£ ¿˝)»´Ã§Úa, b, c§»§∑§∆°¢ {ab, ac, c}§Àåù§π§Î{¶À, a, b, bc, abc} (¶À§œø’§ŒΩM§fl∫œ§Ô§ª) ?§≥§Ï§Ú°∏∑Ò∂®ZDD°π§»∫Ù§÷§≥§»§À§π§Î°£
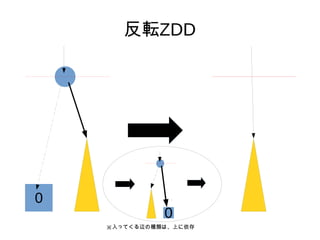
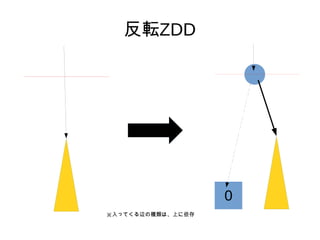
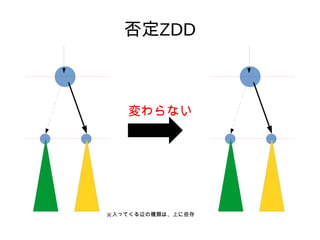
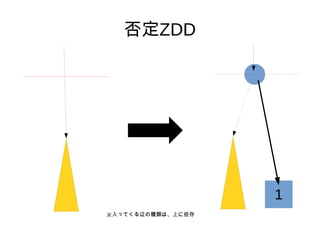
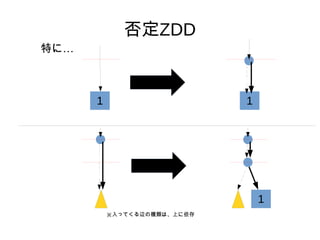
- 12. ∑Ò∂®ZDD °Ò §¢§ÎZDD§´§È°¢§Ω§Œ∑Ò∂®ZDD§Ú◊˜§Î•¢•Î•¥•Í•∫•‡§Úøº§® §Î°£ °Ò §fi§∫°¢“ª∑¨œ¬§Œ°°°°°°°°§»°°°°°°°°§Ú»Î§ÏÃʧ®§Î°£ °Ò ¥Œ§À°¢“‘œ¬§Œ≤Ÿ◊˜§Ú°¢…œ§ŒÌ?fix§´§ÈÌò§À––§¶°£ 0 1
- 18. ∑Ò∂®ZDD °Ò §≥§Ï§È§Œ§≥§»§Ú––§√§ø§¿§±§«§œ°¢–¬§ø§ µ»Å˝Ω” µ„§¨…˙§fi§Ï§Îø…ƒ‹–‘§¨§¢§Í°¢º»ºsZDD§œµ√§È§Ï § §§°£ °Ò ”ãÀ„¡ø§œ°¢O(V * N)§Ø§È§§?(N§œ“™Àÿ ˝)
- 20. øº≤Ï æflÿ˝1 ∑¥‹û ∑Ò∂® ∑Ò∂® ∑¥‹û 0 1 0 1 0 1 0 1 {ab, ac, c} {c, b, ab} {a, abc, b, bc, ¶À} {bc, ¶À, ac, a, abc} a b c a b c a b c a b c
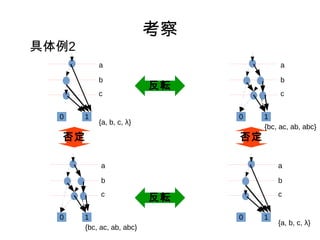
- 22. øº≤Ï æflÿ˝2 ∑¥‹û ∑Ò∂® ∑Ò∂® ∑¥‹û 0 1 0 1 {a, b, c, ¶À} {bc, ac, ab, abc} a b c a b c 0 1 {a, b, c, ¶À} a b c 0 1 {bc, ac, ab, abc} a b c
- 24. §fi§»§· °Ò ∑¥‹û?∑Ò∂®§π§Î§»°¢•∞•È•’§Œ—}Îj§µ§¨â‰§Ô§Î§≥§»§¨§¢ §Î°£“‘œ¬§Œàˆ∫œ°¢—}Îj§À§ §ÎÉAœÚ§¨§¢§Î°£ ∑Ò∂® : ±Ì§∑§∆§§§ÎΩM§fl∫œ§Ô§ª§Œ ˝§¨∂‡§§ ∑¥‹û : flx§÷“™Àÿ§Œ ˝§¨∂‡§§ °˙∑¥‹û?∑Ò∂®§«µ√§È§Ï§Î4§ƒ§ŒZDD§Œ§¶§¡°¢◊Ó§‚ ÖgºÉ§«§¢§Î§»Àº§Ô§Ï§ÎZDD§ÚíQ§¶§Œ§¨¡º§§°£ °Ò ∑¥‹û?∑Ò∂®§ÀÈv§π§Î°¢√¿§∑§§–‘Ÿ|§œ“䧃§±§È§Ï§ §´§√ §ø°£(“䧃§´§Î§»Àº§√§∆§§§ø§Œ§«±Ø§∑§´§√§ø) ¿˝) ∑¥‹û(or∑Ò∂®)§∑§∆§‚°¢°°§Œ ˝§¨â‰§Ô§È§ §§°£ ¿˝) ∑¥‹û§‚∑Ò∂®§‚§∑§øZDD§œ°¢§‚§»§ŒZDD§»°°§¨À∆§∆§§ §Î°£ °Ò §≥§Ï§Ë§Í§‚ÀŸ§§•¢•Î•¥•Í•∫•‡§¨§¢§Î§´§‚§∑§Ï§ §§°£