Replace
- 1. replace ‘≠∞∏£∫komiya Ω‚¥£∫fura2, komiya •π•È•§•…£∫komiya
- 2. ÜñÓ}∏≈“™ °Ò Œƒ◊÷¡–S§¨§¢§Î°£“‘œ¬§Œ•Ø•®•Í§ÚQÇÄÑI¿Ì§π§Î°£ °Ò S§À§ƒ§§§∆°¢Œƒ◊÷c§ÚŒƒ◊÷¡–p§«÷√ìQ§π§Î°£ °Ò ≤ø∑÷Œƒ◊÷¡–S[A..B]§Ú≥ˆ¡¶§π§Î°£ °Ò 1 ®Q Q ®Q 3*10^5 °Ò |S|, |p| ®Q 10 °Ò 1 ®Q A ®Q B ®Q 10^18 °Ò B ®C A ®Q 10^5
- 3. Ω‚∑®(«∞∞Î) °Ò Œƒ◊÷¡–§Ú•∞•È•’(DAG)§√§›§Ø≥÷§ƒ§Ë§¶§À§π§Î°£ °Ò §≥§Œ§»§≠°¢Õ¨§∏Œƒ◊÷§œÕ¨§∏•Œ©`•…§Ú±Ì§π§Ë§¶§À§∑ §∆°¢÷√ìQ§Ú“ªÀ≤§«ÑI¿Ì§«§≠§Î§Ë§¶§À§∑§∆§™§Ø°£
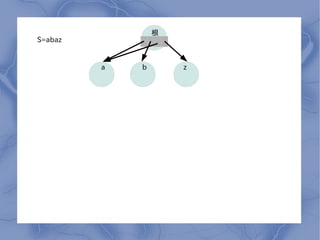
- 4. ∏˘ S=abaz a b z
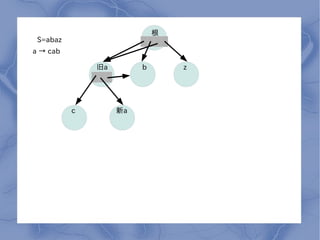
- 5. ∏˘ S=abaz a °˙ cab æ…a b z c –¬a
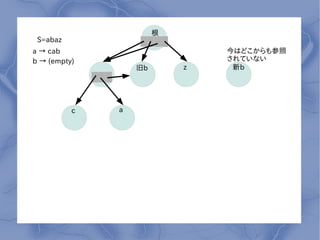
- 6. ∏˘ S=abaz a °˙ cab ΩÒ§œ§…§≥§´§È§‚≤Œ’’ b °˙ (empty) §µ§Ï§∆§§§ §§ æ…b z –¬b c a
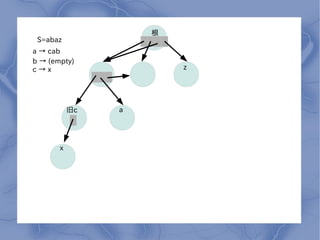
- 7. ∏˘ S=abaz a °˙ cab b °˙ (empty) c°˙x z æ…c a x
- 8. Ω‚∑®(··∞Î) °Ò »´§∆§ŒŒƒ◊÷¡–§Ú•«©`•ø§»§∑§∆±£≥÷§π§Î§≥§»§œ∫Ü Ög§¿§¨°¢§Ω§Œ÷–§´§È10^5Œƒ◊÷≥ˆ¡¶§π§Î§Œ§œ◊¢ “‚§∑§ §§§»TLE§π§Îø…ƒ‹–‘§¨§¢§Î°£ °Ò •∞•È•’§Ú•·•‚ªØÃΩÀ˜§√§›§Øøk∂œ§π§Î§±§…°¢ÈL§µ0 §Œ≤ø∑÷§Úœ˚§∑§ø§Í°¢◊”•Œ©`•…§»◊‘•Œ©`•…§Œ•µ•§•∫ §¨Õ¨§∏ïr§œflmµ±§ÀΩU¬∑àRøs§π§Î§Ë§¶§Àåg◊∞§π §Ï§–§Ë§§°£ °Ò •π•ø•√•Ø•™©`•–©`•’•Ì©`§À§‚◊¢“‚§π§Î§≥§»°£
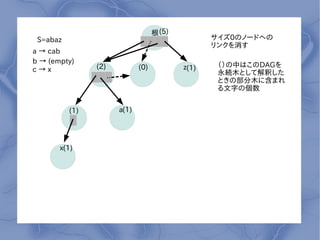
- 9. ∏˘ (5) S=abaz •µ•§•∫0§Œ•Œ©`•…§ÿ§Œ •Í•Û•Ø§Úœ˚§π a °˙ cab b °˙ (empty) (2) (0) z(1) £®£©§Œ÷–§œ§≥§ŒDAG§Ú c°˙x ”¿æAƒæ§»§∑§∆Ω‚·ã§∑§ø §»§≠§Œ≤ø∑÷ƒæ§À∫¨§fi§Ï §ÎŒƒ◊÷§ŒÇÄ ˝ (1) a(1) x(1)
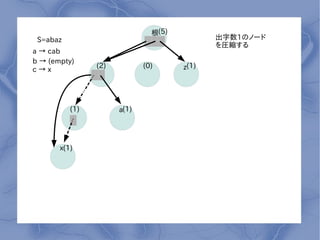
- 10. ∏˘(5) S=abaz ≥ˆ◊÷ ˝1§Œ•Œ©`•… §ÚàRøs§π§Î a °˙ cab b °˙ (empty) (2) (0) z(1) c°˙x (1) a(1) x(1)
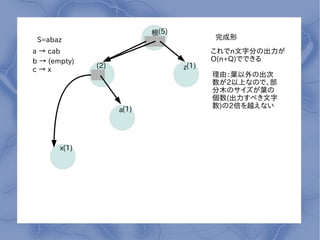
- 11. ∏˘(5) S=abaz ÕÍ≥…–Œ a °˙ cab §≥§Ï§«nŒƒ◊÷∑÷§Œ≥ˆ¡¶§¨ b °˙ (empty) O(n+Q)§«§«§≠§Î (2) z(1) c°˙x ¿Ì”…£∫»~“‘Õ‚§Œ≥ˆ¥Œ ˝§¨2“‘…œ§ §Œ§«°¢≤ø ∑÷ƒæ§Œ•µ•§•∫§¨»~§Œ ÇÄ ˝(≥ˆ¡¶§π§Ÿ§≠Œƒ◊÷ ˝)§Œ2±∂§Ú‘Ω§®§ §§ a(1) x(1)

![ÜñÓ}∏≈“™
°Ò Œƒ◊÷¡–S§¨§¢§Î°£“‘œ¬§Œ•Ø•®•Í§ÚQÇÄÑI¿Ì§π§Î°£
°Ò S§À§ƒ§§§∆°¢Œƒ◊÷c§ÚŒƒ◊÷¡–p§«÷√ìQ§π§Î°£
°Ò ≤ø∑÷Œƒ◊÷¡–S[A..B]§Ú≥ˆ¡¶§π§Î°£
°Ò 1 ®Q Q ®Q 3*10^5
°Ò |S|, |p| ®Q 10
°Ò 1 ®Q A ®Q B ®Q 10^18
°Ò B ®C A ®Q 10^5](https://image.slidesharecdn.com/replace-130313021427-phpapp01/85/Replace-2-320.jpg)