Fungsi Arus dan Kecepatan potensial
- 1. Fungsi Arus dan Kecepatan Potensial M. Jamhuri (m.jamhuri@live.com) March 14, 2013 M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
- 2. Pendahuluan Fungsi arus (ﺵ) Konsep Rumus Terkait Contoh Rotasi Kecepatan Potensial Konsep Rumus Terkait Contoh Hubungan antara fungsi arus dengan kecepatan potensial kecepatan petensial kompleks M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
- 3. Garis Arus Pandang ﺅ؛uida 2D dan tak termampatkan Persamaan kontinuitas ﻗﺵ ﻗﺵu ﻗﺵv ﻗﺵw + + + =0 ﻗt ﻗx ﻗy ﻗz kasus 2D, persamaan diatas menjadi ﺯ ﻗu ﻗv ﻗu + =0 v= ﻗ dy ﻗx ﻗy ﻗx u dan v saling berhubungan. Adakah fungsi yang memenuhi keduanya? M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
- 4. Fungsi Arus Anggap ﻗﺵ u= ﻗy Maka ﺯ ﺯ ﻗu ﻗ2ﺵ v = ﻗ dy = ﻗ dy ﻗx ﻗxﻗy ﺯ ﻗ ﻗﺵ ﻗﺵ = ﻗ dy = ﻗ ﻗy ﻗx ﻗx Sebagai ganti dari dua fungsi u dan v , kita hanya perlu menyelesaikan satu fungsi stream (ﺵ) Orde PDE-nya bertambah satu M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
- 5. Fungsi Arus Apakah yang dimaksud dengan fungsi stream ﺵ? Persamaan untuk garis arus dalam 2D diberikan oleh ﺵ = konstan Garis arus bisa terdapat pada ﺅ؛uida 3D, tetapi tidak dengan fungsi arus Kenapa? (Jika kita bekerja dengan kecepatan potensial, kita akan segera tahu) Dalam 3D, garis arus memenuhi persamaan dx dy dz = = u v w M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
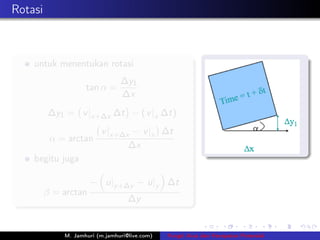
- 6. Rotasi Deﺅ؛nisi Rotasi Anggap v |x < v |x+ﻗx dan u|y < u|y +ﻗy , rotasi di deﺅ؛nisikan sebagai d ﺳﺎ+ﺳﺎ ﺵ= dt 2 M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
- 7. Rotasi untuk menentukan rotasi ﻗy1 tan ﺳﺎ = ﻗx ﻗy1 = v |x+ﻗx ﻗt ﻗ ( v |x ﻗt) v |x+ﻗx ﻗ v |x ﻗt ﺳﺎ = arctan ﻗx begitu juga ﻗ u|y +ﻗy ﻗ u|y ﻗt ﺳﺎ = arctan ﻗy M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
- 8. Rotasi untuk menentukan rotasi ﻗy1 tan ﺳﺎ = ﻗx ﻗy1 = v |x+ﻗx ﻗt ﻗ ( v |x ﻗt) v |x+ﻗx ﻗ v |x ﻗt ﺳﺎ = arctan ﻗx begitu juga ﻗ u|y +ﻗy ﻗ u|y ﻗt ﺳﺎ = arctan ﻗy M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
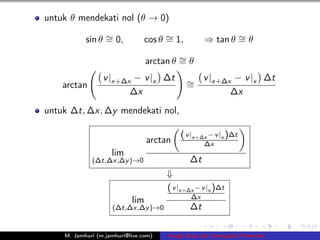
- 9. Menghitung rotasi d ﺳﺎ+ﺳﺎ 1 ﺳﺎ + ﺳﺎ|t+ﻗt ﻗ ﺳﺎ + ﺳﺎ|t ﺵ = = lim dt 2 2 ﻗtﻗ0 ﻗt ( v |x+ﻗx ﻗ v |x )ﻗt arctan ﻗx 1 = lim 2 ﻗt,ﻗx,ﻗy ﻗ0 ﻗt ( u|y +ﻗy ﻗ u|y )ﻗt arctan ﻗy 1 ﻗ lim 2 ﻗt,ﻗx,ﻗy ﻗ0 ﻗt M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
- 10. untuk ﺳﺕ mendekati nol (ﺳﺕ ﻗ 0) sin ﺳﺕ ﻗﺙ 0, = cos ﺳﺕ ﻗﺙ 1, = ﻗ tan ﺳﺕ ﻗﺙ ﺳﺕ = arctan ﺳﺕ ﻗﺙ ﺳﺕ = v |x+ﻗx ﻗ v |x ﻗt ﻗﺙ v |x+ﻗx ﻗ v |x ﻗt arctan = ﻗx ﻗx untuk ﻗt, ﻗx, ﻗy mendekati nol, ( v |x+ﻗx ﻗ v |x )ﻗt arctan ﻗx lim (ﻗt,ﻗx,ﻗy )ﻗ0 ﻗt ﻗ ( v |x+ﻗx ﻗ v |x )ﻗt ﻗx lim (ﻗt,ﻗx,ﻗy )ﻗ0 ﻗt M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
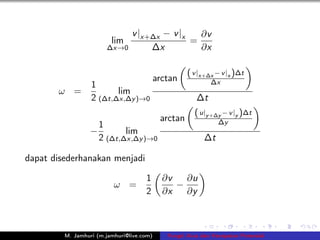
- 11. v |x+ﻗx ﻗ v |x ﻗv lim = ﻗxﻗ0 ﻗx ﻗx ( v |x+ﻗx ﻗ v |x )ﻗt arctan ﻗx 1 ﺵ = lim 2 (ﻗt,ﻗx,ﻗy )ﻗ0 ﻗt ( u|y +ﻗy ﻗ v |y )ﻗt arctan ﻗy 1 ﻗ lim 2 (ﻗt,ﻗx,ﻗy )ﻗ0 ﻗt dapat disederhanakan menjadi 1 ﻗv ﻗu ﺵ = ﻗ 2 ﻗx ﻗy M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
- 12. Rotasi pada Fungsi Arus untuk menuliskan rotasi dalam bentuk fungsi stream ﻗﺵ ﻗﺵ u= v =ﻗ ﻗy ﻗx 1 ﻗv ﻗu ﺵ = ﻗ 2 ﻗx ﻗy 1 ﻗ 2ﺵ ﻗ2ﺵ = ﻗ 2 ﻗ 2 ﻗx ﻗy 2 1 2 = ﻗ ﺵ 2 yaitu 2 ﺵ + 2ﺵ = 0 untuk aliran tak berotasi ﺵ = 0, 2 ﺵ=0 M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
- 13. Rotasi dan Potensial untuk aliran tak berotasi ﺵ = 0 1 ﻗv ﻗu ﻗ = 0 2 ﻗx ﻗy ﻗv ﻗu ﻗ = 0 ﻗx ﻗy Persamaan diatas, seperti persamaan kontinuitas u dan v saling berhubungan Adakah suatu fungsi yang memenuhi hubungan tersebut? M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
- 14. Kecepatan Potensial Anggap ﻗﺵ ﻗﺵ u= , v= ﻗx ﻗy maka ﻗv ﻗu ﻗ2ﺵ = = ﻗx ﻗy ﻗxﻗy dalam 3D, dengan cara yang sama dapat diperoleh ﻗﺵ w= ﻗz ﺵ adalah kecepatan potensial. M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial
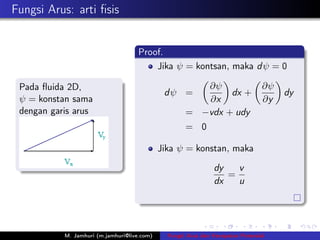
- 15. Fungsi Arus: arti ﺅ؛sis Proof. Jika ﺵ = kontsan, maka d ﺵ = 0 Pada ﺅ؛uida 2D, ﻗﺵ ﻗﺵ dﺵ = dx + dy ﺵ = konstan sama ﻗx ﻗy dengan garis arus = ﻗvdx + udy = 0 Jika ﺵ = konstan, maka dy v = dx u M. Jamhuri (m.jamhuri@live.com) Fungsi Arus dan Kecepatan Potensial