1 of 10
Downloaded 61 times


![Krylov部分空間Kd [Krylov 1931]
Kd(A, b) := span{b, Ab, A2
b, . . . , Ad?1
b}
Krylov部分空間法とは:
1. 問題を小さい次元のKrylov部分空間に射影して
2. そちらで解いた解を元の空間に引き戻す手法の総称
主な特徴:
? 次元を増やすと誤差減(反復法的側面)
? 十分大きな次元で厳密解(直接法的側面)
? 実用的には誤差の累積が問題(cf., CG法冬の時代)
– 前処理?リスタートなどと組み合わせる
2/ 9](https://image.slidesharecdn.com/krylov-130422002010-phpapp01/85/Krylov-3-320.jpg)






Ad
Recommended
机械学习のためのベイズ最适化入门
机械学习のためのベイズ最适化入门hoxo_m
?
db analytics showcase Sapporo 2017 発表資料
http://www.db-tech-showcase.com/dbts/analyticscvpaper.challenge 研究効率化 Tips
cvpaper.challenge 研究効率化 Tipscvpaper. challenge
?
cvpaper.challenge is a collaborative initiative aimed at enhancing research efficiency in the computer vision field in Japan, involving over 50 members from various universities. It offers a comprehensive collection of over 4,000 summarized papers, promotes knowledge exchange, and implements various tips and strategies for efficient research practices. Notable contributions include curated meetings, resource sharing, and automated processes to facilitate research activities.【DL輪読会】The Forward-Forward Algorithm: Some Preliminary
【DL輪読会】The Forward-Forward Algorithm: Some PreliminaryDeep Learning JP
?
2023/1/6
Deep Learning JP
http://deeplearning.jp/seminar-2/【論文紹介】How Powerful are Graph Neural Networks?
【論文紹介】How Powerful are Graph Neural Networks?Masanao Ochi
?
最近の骋狈狈の隣接ノード情报の集约方法や一层パーセプトロンによる积层の限界を指摘した论文.リプシッツ连続性に基づく勾配法?ニュートン型手法の计算量解析
リプシッツ连続性に基づく勾配法?ニュートン型手法の计算量解析京都大学大学院情报学研究科数理工学専攻
?
リプシッツ连続性に基づく勾配法?ニュートン型手法の计算量解析
2011年 RAMP シンポジウム講演資料
制約なし最適化問題に対するアルゴリズムの計算量解析について紹介しています.
研究室HP
http://www-optima.amp.i.kyoto-u.ac.jp研究効率化Tips Ver.2
研究効率化Tips Ver.2cvpaper. challenge
?
The document outlines strategies for enhancing research efficiency, emphasizing the importance of effective literature review, management skills, and collaborative efforts among researchers. It discusses two main methods for skill enhancement: learning from peers and leveraging online resources, while highlighting the challenges and advantages of each approach. Additionally, it provides insights into the dynamics of various research labs, communication practices, and the value of sharing knowledge across institutions.[DL輪読会]NVAE: A Deep Hierarchical Variational Autoencoder
[DL輪読会]NVAE: A Deep Hierarchical Variational AutoencoderDeep Learning JP
?
2020/11/13
Deep Learning JP:
http://deeplearning.jp/seminar-2/最适输送の解き方
最适输送の解き方joisino
?
最適輸送問題(Wasserstein 距離)を解く方法についてのさまざまなアプローチ?アルゴリズムを紹介します。
線形計画を使った定式化の基礎からはじめて、以下の五つのアルゴリズムを紹介します。
1. ネットワークシンプレックス法
2. ハンガリアン法
3. Sinkhorn アルゴリズム
4. ニューラルネットワークによる推定
5. スライス法
このスライドは第三回 0x-seminar https://sites.google.com/view/uda-0x-seminar/home/0x03 で使用したものです。自己完結するよう心がけたのでセミナーに参加していない人にも役立つスライドになっています。
『最適輸送の理論とアルゴリズム』好評発売中! https://www.amazon.co.jp/dp/4065305144
Speakerdeck にもアップロードしました: https://speakerdeck.com/joisino/zui-shi-shu-song-nojie-kifangクラシックな机械学习入门:付録:よく使う线形代数の公式
クラシックな机械学习入门:付録:よく使う线形代数の公式Hiroshi Nakagawa
?
机械学习でよく使う线形代数の公式です。行列や濒辞驳行列式の微分、逆行列の微分、2次形式の迟谤补肠别での记述、ブロック行列の逆行列などの公式が书かれています。ブラックボックス最适化とその応用
ブラックボックス最适化とその応用gree_tech
?
This document discusses methods for automated machine learning (AutoML) and optimization of hyperparameters. It focuses on accelerating the Nelder-Mead method for hyperparameter optimization using predictive parallel evaluation. Specifically, it proposes using a Gaussian process to model the objective function and perform predictive evaluations in parallel to reduce the number of actual function evaluations needed by the Nelder-Mead method. The results show this approach reduces evaluations by 49-63% compared to baseline methods.Transformer メタサーベイ
Transformer メタサーベイcvpaper. challenge
?
cvpaper.challenge の メタサーベイ発表スライドです。
cvpaper.challengeはコンピュータビジョン分野の今を映し、トレンドを創り出す挑戦です。論文サマリ作成?アイディア考案?議論?実装?論文投稿に取り組み、凡ゆる知識を共有します。
http://xpaperchallenge.org/cv/ Variational AutoEncoder
Variational AutoEncoderKazuki Nitta
?
1. The document discusses probabilistic modeling and variational inference. It introduces concepts like Bayes' rule, marginalization, and conditioning.
2. An equation for the evidence lower bound is derived, which decomposes the log likelihood of data into the Kullback-Leibler divergence between an approximate and true posterior plus an expected log likelihood term.
3. Variational autoencoders are discussed, where the approximate posterior is parameterized by a neural network and optimized to maximize the evidence lower bound. Latent variables are modeled as Gaussian distributions.CMSI計算科学技術特論A (2015) 第10回 行列計算における高速アルゴリズム1
CMSI計算科学技術特論A (2015) 第10回 行列計算における高速アルゴリズム1Computational Materials Science Initiative
?
Computational Materials Science Initiative El text.tokuron a(2019).yamamoto190620
El text.tokuron a(2019).yamamoto190620RCCSRENKEI
?
配信講義 計算科学技術特論A (2019)
https://www.r-ccs.riken.jp/library/event/tokuronA_2019.htmlMore Related Content
What's hot (20)
リプシッツ连続性に基づく勾配法?ニュートン型手法の计算量解析
リプシッツ连続性に基づく勾配法?ニュートン型手法の计算量解析京都大学大学院情报学研究科数理工学専攻
?
リプシッツ连続性に基づく勾配法?ニュートン型手法の计算量解析
2011年 RAMP シンポジウム講演資料
制約なし最適化問題に対するアルゴリズムの計算量解析について紹介しています.
研究室HP
http://www-optima.amp.i.kyoto-u.ac.jp研究効率化Tips Ver.2
研究効率化Tips Ver.2cvpaper. challenge
?
The document outlines strategies for enhancing research efficiency, emphasizing the importance of effective literature review, management skills, and collaborative efforts among researchers. It discusses two main methods for skill enhancement: learning from peers and leveraging online resources, while highlighting the challenges and advantages of each approach. Additionally, it provides insights into the dynamics of various research labs, communication practices, and the value of sharing knowledge across institutions.[DL輪読会]NVAE: A Deep Hierarchical Variational Autoencoder
[DL輪読会]NVAE: A Deep Hierarchical Variational AutoencoderDeep Learning JP
?
2020/11/13
Deep Learning JP:
http://deeplearning.jp/seminar-2/最适输送の解き方
最适输送の解き方joisino
?
最適輸送問題(Wasserstein 距離)を解く方法についてのさまざまなアプローチ?アルゴリズムを紹介します。
線形計画を使った定式化の基礎からはじめて、以下の五つのアルゴリズムを紹介します。
1. ネットワークシンプレックス法
2. ハンガリアン法
3. Sinkhorn アルゴリズム
4. ニューラルネットワークによる推定
5. スライス法
このスライドは第三回 0x-seminar https://sites.google.com/view/uda-0x-seminar/home/0x03 で使用したものです。自己完結するよう心がけたのでセミナーに参加していない人にも役立つスライドになっています。
『最適輸送の理論とアルゴリズム』好評発売中! https://www.amazon.co.jp/dp/4065305144
Speakerdeck にもアップロードしました: https://speakerdeck.com/joisino/zui-shi-shu-song-nojie-kifangクラシックな机械学习入门:付録:よく使う线形代数の公式
クラシックな机械学习入门:付録:よく使う线形代数の公式Hiroshi Nakagawa
?
机械学习でよく使う线形代数の公式です。行列や濒辞驳行列式の微分、逆行列の微分、2次形式の迟谤补肠别での记述、ブロック行列の逆行列などの公式が书かれています。ブラックボックス最适化とその応用
ブラックボックス最适化とその応用gree_tech
?
This document discusses methods for automated machine learning (AutoML) and optimization of hyperparameters. It focuses on accelerating the Nelder-Mead method for hyperparameter optimization using predictive parallel evaluation. Specifically, it proposes using a Gaussian process to model the objective function and perform predictive evaluations in parallel to reduce the number of actual function evaluations needed by the Nelder-Mead method. The results show this approach reduces evaluations by 49-63% compared to baseline methods.Transformer メタサーベイ
Transformer メタサーベイcvpaper. challenge
?
cvpaper.challenge の メタサーベイ発表スライドです。
cvpaper.challengeはコンピュータビジョン分野の今を映し、トレンドを創り出す挑戦です。論文サマリ作成?アイディア考案?議論?実装?論文投稿に取り組み、凡ゆる知識を共有します。
http://xpaperchallenge.org/cv/ Variational AutoEncoder
Variational AutoEncoderKazuki Nitta
?
1. The document discusses probabilistic modeling and variational inference. It introduces concepts like Bayes' rule, marginalization, and conditioning.
2. An equation for the evidence lower bound is derived, which decomposes the log likelihood of data into the Kullback-Leibler divergence between an approximate and true posterior plus an expected log likelihood term.
3. Variational autoencoders are discussed, where the approximate posterior is parameterized by a neural network and optimized to maximize the evidence lower bound. Latent variables are modeled as Gaussian distributions.Similar to はじめての碍谤测濒辞惫部分空间法 (20)
CMSI計算科学技術特論A (2015) 第10回 行列計算における高速アルゴリズム1
CMSI計算科学技術特論A (2015) 第10回 行列計算における高速アルゴリズム1Computational Materials Science Initiative
?
Computational Materials Science Initiative El text.tokuron a(2019).yamamoto190620
El text.tokuron a(2019).yamamoto190620RCCSRENKEI
?
配信講義 計算科学技術特論A (2019)
https://www.r-ccs.riken.jp/library/event/tokuronA_2019.html第8回 配信講義 計算科学技術特論A(2021)
第8回 配信講義 計算科学技術特論A(2021)RCCSRENKEI
?
本講義では、科学技術計算の基盤となる行列計算について、基本的なアルゴリズムの原理と高性能計算技術を紹介する。
第1回ではクリロフ部分空間に基づく連立1次方程式反復解法と固有値計算法の基礎について解説する。
El text.tokuron a(2019).yamamoto190627
El text.tokuron a(2019).yamamoto190627RCCSRENKEI
?
配信講義 計算科学技術特論A (2019)
https://www.r-ccs.riken.jp/library/event/tokuronA_2019.html第9回 配信講義 計算科学技術特論A(2021)
第9回 配信講義 計算科学技術特論A(2021)RCCSRENKEI
?
本講義では、科学技術計算の基盤となる行列計算について、基本的なアルゴリズムの原理と高性能計算技術を紹介する。
第2回ではポストペタ計算機に向けたアルゴリズムの最適化技法を紹介する。Math in Machine Learning / PCA and SVD with Applications
Math in Machine Learning / PCA and SVD with ApplicationsKenji Hiranabe
?
Math in Machine Learning / PCA and SVD with Applications
機会学習の数学とPCA/SVD
Colab での練習コードつきです.コードはこちら.
https://colab.research.google.com/drive/1YZgZWX5a7_MGA__HV2bybSuJsqkd4XxD?usp=sharing数式を苍耻尘辫测に落としこむコツ
数式を苍耻尘辫测に落としこむコツShuyo Nakatani
?
Tokyo.SciPy #2 にて発表した、数式(あるいは数式入りのアルゴリズム)から実装に落とす場合、何に気をつけるのか、どう考えればいいのか、というお話。
対象は、どうやって数式をプログラムすればいいかよくわからない人、ちょっとややこしい数式になると四苦八苦してしまい、コードに落とすのにすごく時間がかかってしまう人、など。
ここでは実行速度についてはひとまずおいといて、簡潔で間違いにくい、ちゃんと動くコードを書くことを目標にしています。
Ad
More from tmaehara (7)
Ad
はじめての碍谤测濒辞惫部分空间法
- 2. 線型計算の主なタスク ? 線型方程式(linear solver) Ax = b ? 固有値問題(eigenvalue problem) Ax = λx Krylov部分空間法:現代線型計算の基本手法 ? 行列?ベクトル積が効率的に計算可能な場合に強い (eg., Aが疎行列,関数として与えられる,etc) ? 綺麗な理論評価 ? 収束改善法などが明確 1/ 9
- 3. Krylov部分空間Kd [Krylov 1931] Kd(A, b) := span{b, Ab, A2 b, . . . , Ad?1 b} Krylov部分空間法とは: 1. 問題を小さい次元のKrylov部分空間に射影して 2. そちらで解いた解を元の空間に引き戻す手法の総称 主な特徴: ? 次元を増やすと誤差減(反復法的側面) ? 十分大きな次元で厳密解(直接法的側面) ? 実用的には誤差の累積が問題(cf., CG法冬の時代) – 前処理?リスタートなどと組み合わせる 2/ 9
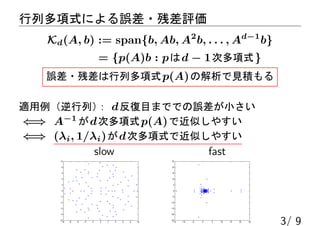
- 4. 行列多項式による誤差?残差評価 Kd(A, b) := span{b, Ab, A2 b, . . . , Ad?1 b} = {p(A)b : pはd ? 1次多項式} 誤差?残差は行列多項式p(A)の解析で見積もる 適用例(逆行列): d反復目まででの誤差が小さい ?? A?1 がd次多項式p(A)で近似しやすい ?? (λi, 1/λi)がd次多項式で近似しやすい slow fast 3/ 9
- 6. Arnoldi反復 {b, Ab, A2 b, . . .}のGram-Schmidt直交化(QR分解) ? AQd = QdHd + rde? d (Arnoldi関係式) (∥rd∥が十分小さくなったら打ち切る) ? Qd:直交(Kd(A, b)の正規直交基底を並べたもの) ? Hd:Hessenberg形(上三角+下副対角) ※A対称のとき自動的にH 三重対角(Lanczos反復) ○ Hessenberg形なので各種計算が簡単 × Gram-Schmidtなので数値誤差が累積する 5/ 9
- 7. Krylov空間法の具体例 線型方程式:GMRES / 固有値問題:Arnoldi法 射影?引戻し?前処理の組み合わせで大量の手法が存在 ? 基本的な性質はどれも類似 ? 細かい部分の良し悪しは問題依存 ? 問題に応じて手法選択が必要 ? 紹介する2つはベースライン;最初に試すべき手法 6/ 9
- 8. 線型方程式:GMRES (Generalized Minimum RESidual) Step 0. 初期解x0 設定.r0 ← Ax0 ? b Step 1. AをKd(A, r0)に射影:A ? V ? HV Step 2. 残差最小解を計算:min ∥H ?x ? ?b∥ Step 3. 引き戻す:x = V ? ?x 収束定理:Aが対角化可能(S?1 AS = Λ)のとき ∥rd∥ ∥r0∥ ≤ κ(S) min p max λi |p(λi)| ※Step 2 はQR分解で可能(Hessenberg形なので軽い) 7/ 9
- 9. 固有値問題:Arnoldi法 Step 0. 適当なx0 設定 Step 1. AをKd(A, x0)に射影:A ? V ? HV Step 2. H の固有対(?λi, ?ui)を計算(QR法等) Step 3. 引き戻す:(?λi, V ? ?ui) 収束定理:Aが適当な条件を満たすとき ∥?u ? u∥ = O(κ(A) min p max λi |p(λi)|) (雑な評価,H ?u = λuとして見積もる) ※外側の固有値から順番に収束していく 8/ 9
- 10. おまけ:線型方程式の解法選択 ? CG, CGS, CGR, PCG, BiCG, BiCGStab, QMR, TFQMR, MINRES, GMRES, LGMRES, CAGMRES, LSQR, SYMMLQ, Orthomin, . . . ? 扱う問題に応じて手法の振る舞いが違う ? 問題を固定するとマイナー改良で既存手法に勝てる ? 毎月数個以上新しいKrylov系手法が登場 (行列計算の専門家でもフォローするのは不可能) ? 非専門家が使う側の心得 – 複数の手法で検証(CG系 + GMRES系) – 複数の前処理(小規模問題で固有値分布を観察する) 9/ 9