�ݺ�ߣ

________________________________________________________________________________
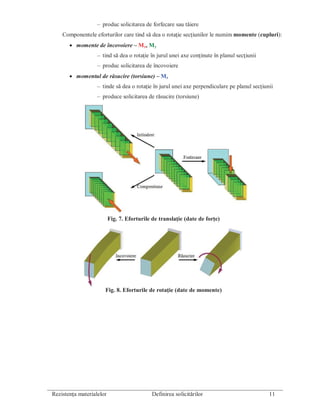
Rezistenţa materialelor Definirea solicitărilor 11
– produc solicitarea de forfecare sau tăiere
Componentele eforturilor care tind să dea o rotaţie secţiunilor le numim momente (cupluri):
• momente de încovoiere – Mx, My
– tind să dea o rotaţie în jurul unei axe conţinute în planul secţiunii
– produc solicitarea de încovoiere
• momentul de răsucire (torsiune) – Mz
– tinde să dea o rotaţie în jurul unei axe perpendiculare pe planul secţiunii
– produce solicitarea de răsucire (torsiune)
Fig. 7. Eforturile de translaţie (date de forţe)
Fig. 8. Eforturile de rotaţie (date de momente)

________________________________________________________________________________
Rezistenţa materialelor Legea lui Hooke 12
III. LEGEA LUI HOOKE
III. 1. Mărimi utilizate
Simbolul Denumirea
Unitatea de
măsură
l lungimea iniţială mm
S secţiunea mm2
Δl alungirea mm
N forţa normală N
ε alungirea specifică –
σ efortul unitar
E modulul de elasticitate longitudinală
III. 2. Generalităţi
Considerăm o bară dreaptă, cu lungimea l şi secţiunea S, fixată la un capăt.
Dacă la capătul celălalt acţionează forţa normală N (în lungul axei barei), bara se va alungi cu
segmentul Δl pe care îl numim alungire.
Fig. 9. Bară solicitată la întindere
Materialele folosite în practică sunt de o mare diversitate, aşadar se vor alungi în mod diferit,
în funcţie de rezistenţa lor la solicitări.
?
Cum putem stabili un criteriu de comparare
între bare din diverse materiale?

________________________________________________________________________________
Această problemă a fost rezolvată experimental de Robert Hooke, cel ce
a stabilit mărimile caracteristice şi legea care le asociază.
Experienţa I
Considerăm două bare drepte, de
aceeaşi secţiune S dar de lungimi diferite (l1,
respectiv l2). Fiecare bară este acţionată de aceeaşi forţă normală N datorită
căreia au aceeaşi alungire Δl.
Pentru a le putea compara utilizăm un raport adimensional, numit alungire specifică ε [–].
Pentru bara nr. 1 Pentru bara nr. 2
Bara nr. 1 este realizată dintr–un material mai rezistent fiindcă are alungirea specifică mai
mică.
OBSERVAŢIE Alungirea specifică reprezintă alungirea unităţii de lungime.
Experienţa II
Considerăm două bare drepte, de aceeaşi lungime l dar
de secţiuni diferite (S1 respectiv S2). Fiecare bară este acţionată
de aceeaşi forţă normală N datorită căreia ele au aceeaşi alungire
Δl.
Ca şi în cazul precedent, vom încerca o comparaţie:
?
Care dintre cele două bare are materialul
mai rezistent?
1
1
l
l
ε ∆=
2
2
l
l
ε ∆=
1 2ε < ε
N
l1Δl
N
l2Δl
S S
Fig. 10. Experienţa I
1 2
?
Care dintre cele două bare are materialul
mai rezistent?
Robert Hooke (1635-1703)
Fig. 11. Experienţa II
1 2
l
S1 S2
N N
Δl

________________________________________________________________________________
Pentru a le putea compara utilizăm un raport, numit efort unitar σ [ ].
Pentru bara nr. 1 Pentru bara nr. 2
Bara nr. 1 este realizată dintr–un material mai rezistent fiindcă are eforul unitar mai mare.
OBSERVAŢIE Efortul unitar reprezintă efortul pe unitatea de suprafaţă.
Putem compara bare drepte de aceeaşi secţiune prin alungirea specifică ε şi bare de aceeaşi
lungime prin efortul unitar σ.
Pentru a compara bare indiferent de dimensiuni, de fapt pentru a compara materiale, trebuie să
găsim o legătură între ε şi σ.
OBSERVAŢII
- Lungimea iniţială şi secţiunea (la deformaţii mici) sunt mărimi
constante.
- Unei forţe normale anumite N îi corespunde o anumită alungire
Δl. Altfel exprimat, unui anumit efort unitar σ îi corespunde o
anumită alungire specifică ε.
Perechile de valori pot fi reprezentate grafic, într–un sistem de axe.
Fig. 12. Curba caracteristică a materialului
Diagrama care rezultă prin încărcarea treptată a barei (până la rupere) se numeşte curba
caracteristică a materialului.
1
1
S
Nσ =
2
2
S
Nσ =
1 2σ > σ

________________________________________________________________________________
Ea este compusă din mai multe zone:
• OE este zona de deformare elastică
E – punctul în care se termină elasticitatea
În această zonă bara descărcată revine la lungimea iniţială (funcţionare în domeniul elastic)
• EC este zona de curgere
C – punctul până la care alungirea creşte sub sarcină constantă (σc)
• CM este zona de întărire
M – punctul la care corespunde efortul unitar maxim (rezistenţa la rupere) σr
• MR este zona de gâtuire şi rupere
R – punctul la care bara se rupe; el dă alungirea specifică la rupere εr
În intervalul ER bara descărcată are lungime mai mare decât lungimea iniţială (funcţionare în
domeniul plastic)
OBSERVAŢII
Curba caracteristică este specifică fiecărui material; ea poate avea
forme diverse.
Putem clasifica materialele în funcţie de comportare astfel:
o după comportarea sub sarcini:
– materiale elastice
– materiale plastice
– materiale elastoplastice (parţial elastice, parţial plastice)
o după mărimea deformaţiilor:
– materiale tenace – au deformaţii plastice mari înainte de a
se rupe
– materiale fragile (casante) – au deformaţii mici înainte de
a se rupe
Din curba caracteristică a unui material ne interesează zona de deformare elastică, în care
dorim să funcţioneze construcţiile tehnice. Aceasta este o dreaptă, pentru care putem scrie ecuaţia:
Constanta se notează cu E şi se numeşte modul de elasticitate longitudinală. Se măsoară, ca şi
efortul unitar, în [ ].
Curba fiind caracteristică fiecărui material, rezultă că şi modulul de elasticitate longitudinală
este caracteristic fiecărui material.
OBSERVAŢII
Curba caracteristică şi legea lui Hooke au fost deduse printr–un
experiment de întindere.
Se pot obţine alte curbe şi alte module de elasticitate prin încercări
de compresiune, torsiune etc.
cons tan t=
ε
σ
E
σ
ε
= Eσ = ε ⋅sau Legea lui Hooke
2
N
mm

________________________________________________________________________________
Unele materiale nu respectă legea lui Hooke (nu au porţiunea
rectilinie 0–E).
În urma încercărilor se obţin caracteristicile mecanice ale
materialelor.
Efortul unitar reprezintă efortul pe unitatea de suprafaţă.

�ݺ�ߣ

Legea lui hooke

Recommended

More Related Content

What's hot (20)

Similar to Legea lui hooke (6)

More from Centre of Excellence in Construction (20)

Legea lui hooke