More Related Content
What's hot (20)
Viewers also liked (20)
Similar to logika matematika (20)
logika matematika
- 4. Contoh : Tentukan Nilai kebenaran dari p => (p v q) p q P v q P => (p v q)
- 5. Kontradiksi Pernyataan majemuk yang semua kemungkinan nilai kebenarannya selalu bernilai salah
- 6. 3. Kontingensi Pernyataan majemuk yang semua kemngkinan nilai kebenarannya bernilai benar atau salah.
- 7. Contoh: Tentukan nilai kebenaran (p V ~q) => ~r p q r ~q ~ r (pV ~q) (pV ~q)=> ~q
- 9. Ekuivalen
- 10. Dua buah pernyataan majemuk yang ekuivalen Untuk memahami pengartian dua buah pernyataan majemuk yang ekuivalen, perhatikan dua buah pernyaan berikut : a = (p v q ) dan b = ( q v p ) Dari pernyataan a dan b itu dapat dibentuk biimplikasi. a <=> b atau (p v q) <=> (q v p) Nilai kebenaran biimplikasi (p v q) <=> (q v p)
- 11. Secara umum dapat disimpulkan : Tautologi yang berbentuk a <=> b dinamakan ekuivalen logis dan dituliskan dengan lambang a b. Dua buah pernyataan majemuk dikatakan ekuivalen, jika kedua pernyataan majemuk itu mempunyai nilai kebenaran yang sama untuk semua kemungkinan nilai kebenaran pernyataan pernyataan komponennya.
- 12. Sifat komutatif a) p v q q v p b) p q q p .................. (4-2) Sifat asosiatif a. (p v q) v r p v (q v r) b. (p q) r p (q r) ..................(4-3) Sifat distributif a) Distributif disjungsi terhadap konjungsi. p v (q r) (p v q) (p v r) b) Distributif konjungsi terhadap dijungsi. p (q v r) (p q) v (p r) ............(4-4)
- 14. Latihan 2. 1. Carilah nilai kebenaran untuk negasi dari (p v q) r dengan tabel kebenaran 2. Tentukanlah negasi dari pernyataan berikut : a. p : Jika Jaka siswa SMA, maka ia lulusan SMP b. p : Jika x = 3, maka x2 = 9 c. p : Jika x 1 > 0, maka x2 5x + 4 > 0 d. p : Semua ayam berbulu hitam e. p : Ada beberapa persamaan kuadrat mempunyai akar imajiner 14
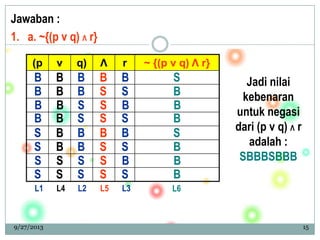
- 15. Jawaban : 1. a. ~{(p v q) r} 9/27/2013 15 S B B B S B B B L6 Jadi nilai kebenaran untuk negasi dari (p v q) r adalah : SBBBSBBB (p v q) r ~ {(p v q) r} B S B S B S B S B S S B B S S B B B B B S S S S B B B B B S B S B S S S B S S S L2 L3L1 L4 L5
- 16. 9/27/2013 16 2. a. p : Jika Jaka siswa SMA, maka ia lulusan SMP ~p : Jika Jaka bukan siswa SMA, maka ia bukan lulusan SMP b. p : Jika x = 3, maka x2 = 9 ~p : Jika x 3, maka x2 9 c. p : Jika x 1 > 0, maka x2 5x + 4 > 0 ~p : Jika x 1 0, maka x 5x + 4 0 d. p : Semua ayam berbulu hitam ~p : Ada beberapa ayam yang berbulu hitam e. p : Ada beberapa persamaan kuadrat mempunyai akar imajiner ~p : Semua persamaan kuadrat mempunyai akar imajiner
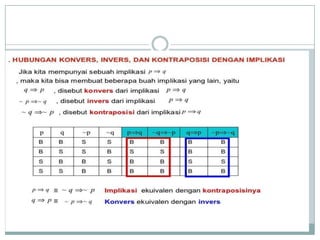
- 17. D. Konvers, Invers, dan Kontraposisi Dari implikasi p q dapat dibentuk implikasi baru : q p disebut konvers dari implikasi semula ~ p ~ q disebut invers dari implikasi semula ~ q ~ p disebut kontraposisi dari implikasi semula
- 19. Contoh : p : Tia penyanyi q : Tia seniman implikasi p q : Jika Tia penyanyi maka Tia seniman Konvers q p : Jika Tia seniman maka Tia penyanyi Invers ~ p ~ q : Jika Tia bukan penyanyi maka Tia bukan seniman Kontraposisi ~ q ~ p : Jika Tia bukan seniman maka Tia bukan penyanyi
- 20. Latihan 1. 1. Carilah nilai kebenaran pernyataan berikut dengan tabel kebenaran a. (p v q) r b. (~q p) (~p v q) c. p (p ~q) 2. Tentukanlah Invers, Konvers dan Kontraposisi dari pernyataan berikut : a. Jika Jaka siswa SMA, maka ia lulusan SMP b. Jika x = 3, maka x2 = 9 c. Jika x 1 > 0, maka x2 5x + 4 > 0 9/27/2013 20
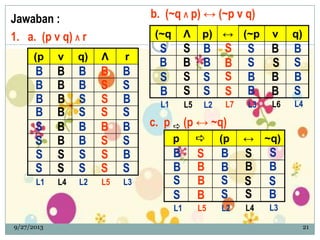
- 21. Jawaban : 1. a. (p v q) r 9/27/2013 21 (p v q) r b. (~q p) (~p v q) (~q p) (~p v q) c. p (p ~q) p (p ~q) B S S B B S S B B S B BS S B B S B S B B S S S B S S S B S B S B S B S B S S B B S S B B B B B S S S S B B B B B S B S B S S S B S S S B B S S B B S S S B S B S S B S S B B B L4L6L2 L3L1 L5 L7 L2 L3L1 L4 L5 L1 L2 L3L4L5
- 22. 2. a. Jika Jaka siswa SMA, maka ia lulusan SMP Invers : Jika Jaka bukan siswa SMA, maka ia bukan lulusan SMP Konvers : Jika Jaka lulusan SMP, maka ia siswa SMA Kontraposisi : Jika Jaka bukan lulusan SMP, maka ia bukan siswa SMA b. Jika x = 3, maka x2 = 9 Invers : Jika x 3, maka x2 9 Konvers : Jika x2 = 9, maka x = 3 Kontraposisi : Jika x2 9, maka x 3 c. Jika x 1 > 0, maka x2 5x + 4 > 0 Invers : Jika x 1 0, maka x 5x + 4 0 Konvers : Jika x 5x + 4 > 0, maka x 1 > 0 Kontraposisi : Jika x 5x + 4 0, maka x 1 0 9/27/2013 22