Έ€ΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩΈ· Έëœ¹ΈΙΈΗΈΦΈΩΈ· - ΈïœÄΈ±ΈΫΈ§ΈΜΈΖœàΈΖ
- 2. βÄΔ ΈùΈ± Έ¥ΈΙΈ±Έ≤Έ§œÉΈΒΈΙœ² ΈΚΈ±ΈΜΈ§ œ¨ΈΜΈΩœÖœ² œ³ΈΩœÖœ² ΈΩœ¹ΈΙœÉΈΦΈΩœçœ², œ³ΈΙœ² Έ±œÄΈΩΈ¥ΈΒΈ·ΈΨΈΒΈΙœ² , œ³Έ± œÉœ΅œ¨ΈΜΈΙΈ± ΈΚΈ±ΈΙ œ³Έ± œÄΈΜΈ±Έ·œÉΈΙΈ± œÄΈΩœÖ œÖœÄΈ§œ¹œ΅ΈΩœÖΈΫ œÉœ³ΈΩ œÉœ΅ΈΩΈΜΈΙΈΚœ¨ Έ≤ΈΙΈ≤ΈΜΈ·ΈΩ. ΈöΈ§œÄΈΩΈΙΈ± Έ±œÄœ¨ Έ±œÖœ³Έ§ ΈΗΈ± ΈΒΈ·ΈΫΈ±ΈΙ œ³ΈΩ 1ΈΩ Έ‰Έ≠ΈΦΈ± œ³ΈΩœÖ Έ¥ΈΙΈ±Έ≥œâΈΫΈ·œÉΈΦΈ±œ³ΈΩœ²! βÄΔ ΈΘΈΒΈΜ.86: Έüœ¹ΈΙœÉΈΦœ¨œ² (ΈΛΈΩ œÉœçΈΫΈΩΈΜΈΩ C œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ Έ±œ¹ΈΙΈΗΈΦœéΈΫ) βÄΔ ΈΘΈΒΈΜ.87: Έüœ¹ΈΙœÉΈΦΈΩΈ· (ΈôœÉœ¨œ³ΈΖœ³Έ± ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ Έ±œ¹ΈΙΈΗΈΦœéΈΫ , Έ™ΈΒœâΈΦΈΒœ³œ¹ΈΙΈΚΈ° œÄΈ±œ¹Έ§œÉœ³Έ±œÉΈΖ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ) βÄΔ ΈΘΈΒΈΜ.88-90: Έ†œ¹Έ§ΈΨΈΒΈΙœ² œÉœ³ΈΩ C. Έ†œ¹ΈΩœÉΈ≠œ΅œâ œ³ΈΙœ² 2 œÄœ¹ΈΩœ³Έ§œÉΈΒΈΙœ² œÉœ³ΈΖ œÉΈΒΈΜ.89 ΈΦΈΒ œ³Έ± Έ≠ΈΫœ³ΈΩΈΫΈ± Έ≥œ¹Έ§ΈΦΈΦΈ±œ³Έ± βÄΔ ΈΘΈΒΈΜ.90: Έüœ¹ΈΙœÉΈΦœ¨œ² (ΈîœçΈΫΈ±ΈΦΈΖ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç) ΈΘΈΒΈΜ.90: ΈëœÄœ¨Έ¥ΈΒΈΙΈΨΈΖ (ΈîœÖΈΫΈ§ΈΦΈΒΈΙœ² œ³ΈΩœÖ i) βÄΔ ΈΘΈΒΈΜ.91: ΈôΈ¥ΈΙœ¨œ³ΈΖœ³ΈΒœ² œÉœÖΈΕœÖΈ≥œéΈΫ (Έ¨ΈΜΈΖ œ³ΈΖ œÉΈΒΈΜΈ·Έ¥Έ±) βÄΔ ΈΘΈΒΈΜ.91: ΈëœÄœ¨Έ¥ΈΒΈΙΈΨΈΖ: πùëß1 + πùëß2 = πùëß1 + πùëß2 βÄΔ ΈΘΈΒΈΜ.92: ΈëœÄœ¨Έ¥ΈΒΈΙΈΨΈΖ (ΈïœÄΈ·ΈΜœÖœÉΈΖ œ³ΈΖœ² Έ±z2 + Έ≤z + Έ≥ = 0) βÄΔ ΈΘΈΒΈΜ.93: Έ†Έ±œ¹Έ±œ³Έ°œ¹ΈΖœÉΈΖ βÄΔ ΈΘΈΒΈΜ.97: Έüœ¹ΈΙœÉΈΦœ¨œ² (Έ€Έ≠œ³œ¹ΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç) βÄΔ ΈΘΈΒΈΜ.97: ΈΛΈΙœ² ΈΙΈ¥ΈΙœ¨œ³ΈΖœ³ΈΒœ² œÄΈΩœÖ Έ≤œ¹Έ·œÉΈΚΈΩΈΫœ³Έ±ΈΙ œÉœ³ΈΩ Έ¥ΈΒœçœ³ΈΒœ¹ΈΩ ΈΦœÄΈΜΈΒ œÄΈΜΈ±Έ·œÉΈΙΈΩ βÄΔ ΈΘΈΒΈΜ.98: œ¨ΈΜΈ± œ³Έ± ΈΦœÄΈΜΈΒ œÄΈΜΈ±Έ·œÉΈΙΈ± βÄΔ ΈΘΈΒΈΜ.98: ΈëœÄœ¨Έ¥ΈΒΈΙΈΨΈΖ: ( |z1 z2| = |z1| |z2| ) βÄΔ ΈΘΈΒΈΜ.99: ΈüΈΙ ΈΒΈΨΈΙœÉœéœÉΈΒΈΙœ²: |z βÄ™ z0| = œ¹ , œ¹ > 0 ΈΚΈ±ΈΙ |z βÄ™ z1| = |z βÄ™ z2| βÄΔ ΈΘΈΒΈΜ.124-5: œ³ΈΙœ² ΈΒœ¹œâœ³Έ°œÉΈΒΈΙœ² ΈΚΈ±œ³Έ±ΈΫœ¨ΈΖœÉΈΖœ² Έ½ ΈΗΈΒœâœ¹Έ·Έ± œÉœ³ΈΩ œÉœ΅ΈΩΈΜΈΙΈΚœ¨ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 3. ΈïΈΠΈëΈΓΈ€ΈüΈ™ΈïΈΘ ΈîΈΙΈ±Έ≤Έ§ΈΕœâ œ³ΈΙœ² 2 ΈΒœÜΈ±œ¹ΈΦΈΩΈ≥Έ≠œ² œÉΈΒΈΜ.93-94 ΈΚΈ±ΈΙ œ³ΈΙœ² 2 ΈΒœÜΈ±œ¹ΈΦΈΩΈ≥Έ≠œ² œÉΈΒΈΜ. 99-100 œÉœ΅ΈΩΈΜΈΙΈΚΈΩœç ΈëΈΘΈöΈ½ΈΘΈïΈôΈΘ ΈΘΈßΈüΈ¦ΈôΈöΈüΈΞ ΈîœÖΈΫΈ§ΈΦΈΒΈΙœ² 8Έë/95, 3Έ£/96, 4Έ£/96, 7Έ£/96 ΈïΈΨΈΙœÉœéœÉΈΒΈΙœ²- ΈΛœçœÄΈΩΈΙ Vieta 14A/96 z: œÄœ¹Έ±Έ≥ΈΦΈ±œ³ΈΙΈΚœ¨œ² z : œÜΈ±ΈΫœ³Έ±œÉœ³ΈΙΈΚœ¨œ² 11Έë/96, 6Έ£/96, 8Έ£/96 ΈôΈ¥ΈΙœ¨œ³ΈΖœ³ΈΒœ² ΈΦΈ≠œ³œ¹œâΈΫ 9Έë/101, 1Έ£/101, 7Έ£/102, 10Έ£/102 Έ™ΈΒœâΈΦΈΒœ³œ¹ΈΙΈΚΈΩΈ· œ³œ¨œÄΈΩΈΙ Έïœçœ¹ΈΒœÉΈΖ Έ≥œ¹Έ±ΈΦΈΦΈ°œ² œÄΈΩœÖ ΈΚΈΙΈΫΈΩœçΈΫœ³Έ±ΈΙ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç 12Έë/96, 9Έ£/97, 4Έë/101, 5Έë/101, 6Έë/101, 8Έë/101, 2Έ£/101, 3Έ£/101, 4Έ£/102, 5Έ£/102, 6Έ£/102, 9Έ£/102, 1Έ™/123, 6Έ™/103 Έ€Έ≠Έ≥ΈΙœÉœ³ΈΩ βÄ™ ΈïΈΜΈ§œ΅ΈΙœÉœ³ΈΩ ΈΦΈ≠œ³œ¹ΈΩ 7Έë/101, 8Έ£/102, 3Έ™/123 ΈöΈ±œ³ΈΖΈ≥ΈΩœ¹Έ·ΈΒœ² Έ±œÉΈΚΈ°œÉΈΒœâΈΫ œÉœ³ΈΩ œÉœ΅ΈΩΈΜΈΙΈΚœ¨ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 4. ΈîœÖΈΫΈ§ΈΦΈΒΈΙœ² œ³ΈΩœÖ i οÄ® οÄ© * œ¹ 4œ¹ + œÖ 4œ¹ΈΫ œÖ 4 œÖ œÖ , ΈΫ Έù , ΈΫ = 4œ¹ + œÖ ΈΦΈΒ 0 œÖ < 4 1 , Έ±ΈΫ œÖ = 0 i , Έ±ΈΫ œÖ = 1 i = i = i i = i i = i = - 1 , Έ±ΈΫ œÖ = 2 - i , Έ±ΈΫ œÖ = 3 οɧ οÉ· οÉ· οÉé ο²ΘοÉ≠ οÉ· οÉ·οÉ° 2015 =i 2 3 1996 ... =i i i iοɽ οɽ οɽ οɽ Έ£œ¹ΈΒœ² œ³ΈΙœ² Έ¥œÖΈΫΈ§ΈΦΈΒΈΙœ²: iοÄ≠ 1οÄ≠ ΈëœÄΈ±ΈΫœ³Έ°œÉΈΒΈΙœ² ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 5. ΈΞœÄΈΩΈΜœ¨Έ≥ΈΙœÉΈΒ œ³Έ± œÄΈ±œ¹Έ±ΈΚΈ§œ³œâ: ΈëœÄΈ±ΈΫœ³Έ°œÉΈΒΈΙœ² 1 + πùë• 2 1 β࣠πùë• 2 πùëé + πùëéπùë• 2 πùëé β࣠πùëéπùë• 2 πùëé 3 + πùëéπùë• 3 πùëé + πùëé 3πùë• 3 1 β࣠πùë• 20 2 3 + 2πùë• 3 2i 2iοÄ≠ 2 2Έ± i 2 2Έ± iοÄ≠ 3 8a i 3 8aοÄ≠ 10 2οÄ≠ 64i ΈîœÖΈΫΈ§ΈΦΈΒΈΙœ² œ³ΈΩœÖ Έ± Έ±i, Έ± Έ± πùüë i , Έ± πùüë Έ± i ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 6. z + πù£¦ , z - πù£¦ z+z=2Re(z) οɽz-z=2Im(z)i ΈΘœÖΈΦœÄΈΜΈ°œ¹œâœÉΈΒ œ³Έ± œÄΈ±œ¹Έ±ΈΚΈ§œ³œâ: ΈëœÄΈ§ΈΫœ³ΈΖœÉΈΖ z w + z w z w - z w z z w w οÄΪ z z w w οÄ≠ 2Re(z w) 2Im(z w) i 2Re z w οÉΠ οÉΕ οÉß οÉΖ οÉ® οÉΗ 2Im i z w οÉΠ οÉΕ οÉß οÉΖ οÉ® οÉΗ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 7. βÄΔ ΈëΈΫ z=z1+z2i ΈΦΈΒ z1 , z2 C, œ³œ¨œ³ΈΒ: πùëß = πùëß1 β࣠πùëß2 πùë• βÄΔ ΈïΈ·ΈΫΈ±ΈΙ ΈΜΈ§ΈΗΈΩœ² ΈΫΈ± œÄΈΒΈΙœ²: πùëß = πùëß1 β࣠πùëß2 πùë• , Έ¥ΈΙœ¨œ³ΈΙ ΈΩ z Έ¥ΈΒΈΫ ΈΒΈ·ΈΫΈ±ΈΙ œÉΈΒ ΈΚΈ±ΈΫΈΩΈΫΈΙΈΚΈ° ΈΦΈΩœ¹œÜΈ°. βÄΔ ΈîΈΒΈΫ ΈΙœÉœ΅œçΈΒΈΙ ΈΖ Έ¥ΈΙΈ§œ³Έ±ΈΨΈΖ œÉœ³ΈΩœÖœ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœçœ². (ΈîΈΖΈΜΈ±Έ¥Έ° Έ¥ΈΒΈΫ Έ≠œ΅ΈΒΈΙ ΈΫœ¨ΈΖΈΦΈ± ΈΖ œÉœ΅Έ≠œÉΈΖ z1 < z2 ΈΦΈΒ z1 , z2 C ) Έ†œ¹ΈΩœÉΈ≠œ΅œâ ! ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 8. βÄΔ ΈëΈΫ Έî < 0 œ³œ¨œ³ΈΒ Έ≠œ΅ΈΒΈΙ Έ¥œçΈΩ œÉœÖΈΕœÖΈ≥ΈΒΈ·œ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈ≠œ² ΈΜœçœÉΈΒΈΙœ² : πù£¦ πùüè,πùüê = βà£πù€Ζ¬± βà£πùöΪ πù£ä πùüêπù€Ε βÄΔ Έ†œ¹œ¨œÉΈΒΈΨΈΒ œ¨œ³ΈΙ Έ≥ΈΙΈ± ΈΫΈ± œ΅œ¹ΈΖœÉΈΙΈΦΈΩœÄΈΩΈΙΈ°œÉΈΒΈΙœ² œ³ΈΩΈΫ œÄΈ±œ¹Έ±œÄΈ§ΈΫœâ œ³œçœÄΈΩ œÄœ¹Έ≠œÄΈΒΈΙ œ³Έ± Έ±, Έ≤, Έ≥ ΈΫΈ± ΈΒΈ·ΈΫΈ±ΈΙ œÄœ¹Έ±Έ≥ΈΦΈ±œ³ΈΙΈΚΈΩΈ· Έ±œ¹ΈΙΈΗΈΦΈΩΈ·! βÄΔ ΈüΈΙ ΈΜœçœÉΈΒΈΙœ² ΈΒΈ·ΈΫΈ±ΈΙ œÉœÖΈΕœÖΈ≥ΈΒΈ·œ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩΈ·, Έ§œ¹Έ±: z1+ z2= 2Re(z1) ΈΚΈ±ΈΙ z1z2=|z1|2 βÄΔ ΈôœÉœ΅œçΈΩœÖΈΫ ΈΚΈ±ΈΙ ΈΩΈΙ œ³œçœÄΈΩΈΙ Vieta: πù£¦ πùüè + πù£¦ πùüê = βà£πù€Ζ πù€Ε ΈΚΈ±ΈΙ πù£¦ πùüè πù£¦ πùüê = πù€Η πù€Ε βÄΔ Έ™ΈΙΈ± ΈΒΈΨΈ§œÉΈΚΈΖœÉΈΖ : βÄΔ 1. Έ§œÉΈΚΈΖœÉΈΖ Έë14 œÉΈΒΈΜΈ·Έ¥Έ± 96 œÉœ΅ΈΩΈΜΈΙΈΚΈΩœç. βÄΔ 2. ΈùΈ± ΈΜœÖΈΗΈΒΈ· ΈΖ ΈΒΈΨΈ·œÉœâœÉΈΖ: z2 βÄ™ i z + 2 = 0 , z C. Έ†œ¹ΈΩœÉΈ≠œ΅œâ ! βÄΔ ΈïœÄΈ·ΈΜœÖœÉΈΖ œ³ΈΖœ² ΈΒΈΨΈ·œÉœâœÉΈΖœ² : Έ±z2 + Έ≤z + Έ≥ = 0 ΈΦΈΒ Έ±, Έ≤, Έ≥ R ΈΚΈ±ΈΙ Έ± β↠0 ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 9. βÄΔ ΈëΈΫ ΈΖ ΈΒΈΨΈ·œÉœâœÉΈΖ œÄΈΒœ¹ΈΙΈ≠œ΅ΈΒΈΙ ΈΦœ¨ΈΫΈΩ œ³ΈΩΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœ¨ z ΈΚΈ±ΈΙ ΈΒΈ·ΈΫΈ±ΈΙ Έ¥ΈΒœÖœ³ΈΒœ¹ΈΩΈ≤Έ§ΈΗΈΦΈΙΈ± ΈΦΈΒ œÄœ¹Έ±Έ≥ΈΦΈ±œ³ΈΙΈΚΈΩœçœ² œÉœÖΈΫœ³ΈΒΈΜΈΒœÉœ³Έ≠œ² , œ΅œ¹ΈΖœÉΈΙΈΦΈΩœÄΈΩΈΙΈΩœçΈΦΈΒ œ³ΈΩœÖœ² œ³œçœÄΈΩœÖœ² œ³ΈΖœ² Έ¥ΈΒœÖœ³ΈΒœ¹ΈΩΈ≤Έ§ΈΗΈΦΈΙΈ±œ² ,ΈΒΈΫœé Έ±ΈΫ ΈΒΈ·ΈΫΈ±ΈΙ ΈΦΈΒΈ≥Έ±ΈΜœçœ³ΈΒœ¹ΈΩœÖ Έ≤Έ±ΈΗΈΦΈΩœç ΈΚΈ§ΈΫΈΩœÖΈΦΈΒ Έ±ΈΫ Έ≥Έ·ΈΫΈΒœ³Έ±ΈΙ œÄΈ±œ¹Έ±Έ≥ΈΩΈΫœ³ΈΩœÄΈΩΈ·ΈΖœÉΈΖ. βÄΔ ΈëΈΫ ΈΖ ΈΒΈΨΈ·œÉœâœÉΈΖ œÄΈΒœ¹ΈΙΈ≠œ΅ΈΒΈΙ œ³ΈΩœÖœ² z ΈΚΈ±ΈΙ πùëß Έ° ΈΚΈ±ΈΙ Έ¥œÖΈΫΈ§ΈΦΈΒΈΙœ² œ³ΈΩœÖœ² ,œ³œ¨œ³ΈΒ ΈΗΈ≠œ³ΈΩœÖΈΦΈΒ z = x + y i ΈΚΈ±ΈΙ Έ≤œ¹Έ·œÉΈΚΈΩœÖΈΦΈΒ œ³Έ± x , y. Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ Έ™ΈΙΈ± œ³ΈΖΈΫ ΈΒœÄΈ·ΈΜœÖœÉΈΖ ΈΒΈΨΈΙœÉœéœÉΈΒœâΈΫ œÉœ³ΈΩ œÉœçΈΫΈΩΈΜΈΩ œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ Έ±œ¹ΈΙΈΗΈΦœéΈΫ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 10. βÄΔ Έ™ΈΙΈ± ΈΫΈ± Έ¥ΈΒΈ·ΈΨΈΩœÖΈΦΈΒ œ¨œ³ΈΙ ΈΩ z ΈΒΈ·ΈΫΈ±ΈΙ œÄœ¹Έ±Έ≥ΈΦΈ±œ³ΈΙΈΚœ¨œ² : βÄΔ œ³ΈΩΈΫ Έ≥œ¹Έ§œÜΈΩœÖΈΦΈΒ œÉœ³ΈΖ ΈΦΈΩœ¹œÜΈ° z = Έ± + Έ≤i ΈΚΈ±ΈΙ Έ±œÄΈΩΈ¥ΈΒΈΙΈΚΈΫœçΈΩœÖΈΦΈΒ œ¨œ³ΈΙ: Έ≤ = 0 Έ° Έ¥ΈΒΈ·œ΅ΈΫΈΩœÖΈΦΈΒ œ¨œ³ΈΙ: πù£¦ = πù£¦ . βÄΔ Έ™ΈΙΈ± ΈΫΈ± Έ¥ΈΒΈ·ΈΨΈΩœÖΈΦΈΒ œ¨œ³ΈΙ ΈΩ z ΈΒΈ·ΈΫΈ±ΈΙ œÜΈ±ΈΫœ³Έ±œÉœ³ΈΙΈΚœ¨œ² : œ³ΈΩΈΫ Έ≥œ¹Έ§œÜΈΩœÖΈΦΈΒ œÉœ³ΈΖ ΈΦΈΩœ¹œÜΈ° z = Έ± + Έ≤i ΈΚΈ±ΈΙ Έ±œÄΈΩΈ¥ΈΒΈΙΈΚΈΫœçΈΩœÖΈΦΈΒ œ¨œ³ΈΙ: Έ± = 0 Έ° Έ¥ΈΒΈ·œ΅ΈΫΈΩœÖΈΦΈΒ œ¨œ³ΈΙ: πù£¦ = - πù£¦ . βÄΔ Έ™ΈΙΈ± ΈΒΈΨΈ§œÉΈΚΈΖœÉΈΖ : βÄΔ ΈëΈΫ z , w ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩΈ· ΈΦΈΒ |z|=|w|= 3 , ΈΫΈ± Έ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ ΈΩ z1= πùëß βà£πùëΛ 3+πùëß πùëΛ ΈΒΈ·ΈΫΈ±ΈΙ œÜΈ±ΈΫœ³Έ±œÉœ³ΈΙΈΚœ¨œ². Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 11. βÄΔ ΈΘœ³ΈΩ œÉœçΈΫΈΩΈΜΈΩ œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ Έ±œ¹ΈΙΈΗΈΦœéΈΫ ΈΦœÄΈΩœ¹ΈΒΈ· ΈΫΈ± Έ±ΈΜΈΖΈΗΈΒœçΈΒΈΙ ΈΦΈΙΈ± ΈΙœÉœ¨œ³ΈΖœ³Έ± œ³ΈΖœ² ΈΦΈΩœ¹œÜΈ°œ²: z1 2 + z2 2 = 0 ΈΚΈ±ΈΙ œ¨œ³Έ±ΈΫ z1β↠0 ΈΚΈ±ΈΙ z2 β↠0 . βÄΔ Έ¨œ³Έ±ΈΫ Έ¥Έ·ΈΫΈΒœ³Έ±ΈΙ ΈΖ œÉœ΅Έ≠œÉΈΖ z1 2 + z2 2 = 0, œ³œ¨œ³ΈΒ ΈΦœÄΈΩœ¹ΈΩœçΈΦΈΒ ΈΫΈ± œ³ΈΖ Έ≥œ¹Έ§œàΈΩœÖΈΦΈΒ œâœ² ΈΒΈΨΈ°œ²: βÄΔ πùëß1 2 + πùëß2 2 = 0 πùëß1 2 - i2 πùëß2 2 = 0 βÄΔ (z1 + iz2) (z1 βÄ™ iz2) = 0 βÄΔ z1 = -iz2 Έ° z1 = iz2 βÄΔ ΈïœÄΈ·œÉΈΖœ² œÄΈ±œ¹Έ±œ³Έ°œ¹ΈΖœÉΈΒ œ¨œ³ΈΙ: βÄ™iz2= πùëß2 πùë• Έ†œ¹ΈΩœÉΈΩœ΅Έ°! ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 12. βÄΔ ΈëΈΫœ³ΈΙœÉœÖΈΕœÖΈ≥Έ°œ² βÄΔ ΈëΈΫ z = Έ± + Έ≤i , Έ± , Έ≤ R œ³œ¨œ³ΈΒ œâœ² Έ±ΈΫœ³ΈΙœÉœÖΈΕœÖΈ≥Έ°œ² œ³ΈΩœÖ z ΈΩœ¹Έ·ΈΕΈΒœ³Έ±ΈΙ ΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœ¨œ²: w = Έ≤ βÄ™ Έ±i (Έ° w = - Έ≤ + Έ±i ). βÄΔ Έ†Έ±œ¹Έ±œ³ΈΖœ¹ΈΩœçΈΦΈΒ œ¨œ³ΈΙ: Έ≤ βÄ™ Έ±i = -i(Έ± + Έ≤i) Έ¥ΈΖΈΜΈ±Έ¥Έ° w = -i z Έ± + Έ≤i = i(Έ≤ βÄ™ Έ±i) Έ¥ΈΖΈΜΈ±Έ¥Έ° z = i w -Έ≤ + Έ±i = i(Έ± + Έ≤i) Έ¥ΈΖΈΜΈ±Έ¥Έ° -w = i z βÄΔ Έ™ΈΙΈ± œÄΈ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ±: z 4ΈΚ+2 + w 4ΈΚ+2 = ( i w )4ΈΚ+2 + w 4ΈΚ+2 = - w 4ΈΚ+2 + w 4ΈΚ+2 = 0 βÄΔ Έ™ΈΙΈ± ΈΒΈΨΈ§œÉΈΚΈΖœÉΈΖ: βÄΔ ΈΞœÄΈΩΈΜœ¨Έ≥ΈΙœÉΈΒ œ³ΈΖΈΫ œÄΈ±œ¹Έ§œÉœ³Έ±œÉΈΖ: (3-i)2010 + (1+3i)2010 Έ‰œÖΈΦΈ§ΈΦΈ±ΈΙ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 13. βÄΔ Έ€ΈΙΈ± Έ±œÉΈΚΈΖœÉΈΩœçΈΜΈ± Έ≥ΈΙΈ± ΈΒΈΨΈ§œÉΈΚΈΖœÉΈΖ œÉœ³ΈΙœ² Έ¥œÖΈΫΈ§ΈΦΈΒΈΙœ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ: βÄΔ ΈîΈ·ΈΫΈΩΈΫœ³Έ±ΈΙ ΈΩΈΙ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩΈ· z1 , z2 β↠0 ΈΦΈΒ πùëß1 πùëß2 + πùëß2 πùëß1 = 1. βÄΔ ΈùΈ± Έ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ: βÄΔ Έ±. πùëß1 3= -πùëß2 3 βÄΔ Έ≤ . πùëß1 πùëß2 2010 + πùëß2 πùëß1 2010 = 2 ΈïΈΨΈ§œÉΈΚΈΖœÉΈΖ œÉœ³ΈΙœ² Έ¥œÖΈΫΈ§ΈΦΈΒΈΙœ² ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 14. βÄΔ Έ€Έ≠œ³œ¹ΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç βÄΔ Έ±ΈΫ z = Έ± + Έ≤ i , œ³œ¨œ³ΈΒ: |z|= πù€Ε πùüê + πù€Ζ πùüê βÄΔ ΈôΈ¥ΈΙœ¨œ³ΈΖœ³ΈΒœ² βÄΔ |z|= |-z|=|πù£¦| βÄΔ |z|2 = z πù£¦ βÄΔ |z1 z2|=|z1||z2| βÄΔ πù£¦ πùüè πù£¦ πùüê = πù£¦ πùüè πù£¦ πùüê , z2βâ†0 βÄΔ Έ†œ¹œ¨œÉΈΒΈΨΈΒ ΈΒœÄΈ·œÉΈΖœ²: |iz| = |i| |z| = |z| βÄΔ ΈöΈ±ΈΙ ΈΦΈΙΈ± Έ±œÉΈΚΈΖœÉΈΩœçΈΜΈ± œÉœ³Έ± ΈΦΈ≠œ³œ¹Έ±: βÄΔ ΈîΈ·ΈΫΈΩΈΫœ³Έ±ΈΙ ΈΩΈΙ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩΈ· z1 , z2 , z3 ΈΦΈΒ: z1 = 1, z2 = 3, z3 = 5 ΈùΈ± Έ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ:|z1 + z2 + z3|= 1 15 |z2z3+9z1z3+25z1z2| Έ‰œÖΈΦΈ§ΈΦΈ±ΈΙ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 15. βÄΔ Έ€Έ≠œ³œ¹ΈΩ Έ±ΈΗœ¹ΈΩΈ·œÉΈΦΈ±œ³ΈΩœ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ βÄΔ ||z1|-|z2|| |z1 + z2| |z1|+|z2| βÄΔ Έßœ¹ΈΖœÉΈΙΈΦΈΩœÄΈΩΈΙΈΒΈ·œ³Έ±ΈΙ ΈΚœÖœ¹Έ·œâœ² Έ≥ΈΙΈ± Έ±œÄœ¨Έ¥ΈΒΈΙΈΨΈΖ Έ±ΈΫΈΙœÉΈΩœ³ΈΙΈΚœéΈΫ œÉœ΅Έ≠œÉΈΒœâΈΫ. βÄΔ Έ†Έ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ± βÄΔ ΈëΈΫ |z|=2 ΈΦΈΒ z C ΈΚΈ±ΈΙ w = 3 βÄ™ 4i , ΈΫΈ± Έ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ: 3 |z+w| 7 Έ‰œÖΈΦΈ§ΈΦΈ±ΈΙ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 16. βÄΔ Έ€Έ≠œ³œ¹ΈΩ Έ¥ΈΙΈ±œÜΈΩœ¹Έ§œ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ βÄΔ ΈëΈΫ z1 , z2 ΈΒΈ·ΈΫΈ±ΈΙ Έ¥œçΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩΈ· Έ±œ¹ΈΙΈΗΈΦΈΩΈ· ΈΚΈ±ΈΙ Έ€1 , Έ€2 ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³ΈΩœÖœ² œÉœ³ΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœ¨ ΈΒœÄΈ·œÄΈΒΈ¥ΈΩ Έ±ΈΫœ³Έ·œÉœ³ΈΩΈΙœ΅Έ± , œ³œ¨œ³ΈΒ |z1 βÄ™ z2| = (M1M2) , Έ¥ΈΖΈΜΈ±Έ¥Έ° œ³ΈΩ ΈΦΈ≠œ³œ¹ΈΩ œ³ΈΖœ² Έ¥ΈΙΈ±œÜΈΩœ¹Έ§œ² Έ¥œçΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ ΈΒΈ·ΈΫΈ±ΈΙ Έ·œÉΈΩ ΈΦΈΒ œ³ΈΖΈΫ Έ±œÄœ¨œÉœ³Έ±œÉΈΖ œ³œâΈΫ ΈΒΈΙΈΚœ¨ΈΫœâΈΫ œ³ΈΩœÖœ². βÄΔ ΈïœÄΈ·œÉΈΖœ² ΈΙœÉœ΅œçΈΒΈΙ: ||z1|-|z2|| |z1 - z2| |z1|+|z2| βÄΔ Έ†Έ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ± βÄΔ ΈëΈΫ Έ≥ΈΙΈ± œ³ΈΩœÖœ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœçœ² z1 , z2 , z3 ΈΙœÉœ΅œçΈΒΈΙ: |z1|=|z2|=|z3|=1 ΈΚΈ±ΈΙ z1+z2+z3=1, ΈΫΈ± Έ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ : βÄΔ Έ±) πùüè πù£¦ πùüè + πùüè πù£¦ πùüê + πùüè πù£¦ πùüë = 1 βÄΔ Έ≤) |z1 βÄ™ 2z2|2 9 βÄΔ Έ≥) Re(πùëß1 πùëß2) -1 Έ‰œÖΈΦΈ§ΈΦΈ±ΈΙ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
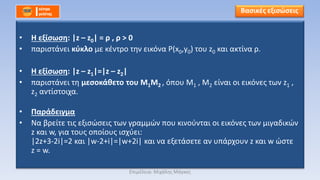
- 17. βÄΔ Έ½ ΈΒΈΨΈ·œÉœâœÉΈΖ: |z βÄ™ z0| = œ¹ , œ¹ > 0 βÄΔ œÄΈ±œ¹ΈΙœÉœ³Έ§ΈΫΈΒΈΙ ΈΚœçΈΚΈΜΈΩ ΈΦΈΒ ΈΚΈ≠ΈΫœ³œ¹ΈΩ œ³ΈΖΈΫ ΈΒΈΙΈΚœ¨ΈΫΈ± ΈΓ(x0,y0) œ³ΈΩœÖ z0 ΈΚΈ±ΈΙ Έ±ΈΚœ³Έ·ΈΫΈ± œ¹. βÄΔ Έ½ ΈΒΈΨΈ·œÉœâœÉΈΖ: |z βÄ™ z1|=|z βÄ™ z2| βÄΔ œÄΈ±œ¹ΈΙœÉœ³Έ§ΈΫΈΒΈΙ œ³ΈΖ ΈΦΈΒœÉΈΩΈΚΈ§ΈΗΈΒœ³ΈΩ œ³ΈΩœÖ Έ€1Έ€2 , œ¨œÄΈΩœÖ Έ€1 , Έ€2 ΈΒΈ·ΈΫΈ±ΈΙ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ z1 , z2 Έ±ΈΫœ³Έ·œÉœ³ΈΩΈΙœ΅Έ±. βÄΔ Έ†Έ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ± βÄΔ ΈùΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ œ³ΈΙœ² ΈΒΈΨΈΙœÉœéœÉΈΒΈΙœ² œ³œâΈΫ Έ≥œ¹Έ±ΈΦΈΦœéΈΫ œÄΈΩœÖ ΈΚΈΙΈΫΈΩœçΈΫœ³Έ±ΈΙ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ z ΈΚΈ±ΈΙ w, Έ≥ΈΙΈ± œ³ΈΩœÖœ² ΈΩœÄΈΩΈ·ΈΩœÖœ² ΈΙœÉœ΅œçΈΒΈΙ: |2z+3-2i|=2 ΈΚΈ±ΈΙ |w-2+i|=|w+2i| ΈΚΈ±ΈΙ ΈΫΈ± ΈΒΈΨΈΒœ³Έ§œÉΈΒœ³ΈΒ Έ±ΈΫ œÖœÄΈ§œ¹œ΅ΈΩœÖΈΫ z ΈΚΈ±ΈΙ w œéœÉœ³ΈΒ z = w. Έ£Έ±œÉΈΙΈΚΈ≠œ² ΈΒΈΨΈΙœÉœéœÉΈΒΈΙœ² ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 18. βÄΔ Έ½ ΈΒΈΨΈ·œÉœâœÉΈΖ: |z βÄ™ z1| + |z βÄ™ z2| = 2Έ± , Έ± > 0 βÄΔ Έ†Έ±œ¹ΈΙœÉœ³Έ§ΈΫΈΒΈΙ Έ≠ΈΜΈΜΈΒΈΙœàΈΖ ΈΦΈΒ ΈΒœÉœ³Έ·ΈΒœ² Έ€1 , Έ€2 œ¨œÄΈΩœÖ Έ€1 , Έ€2 ΈΒΈ·ΈΫΈ±ΈΙ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ z1 , z2 Έ±ΈΫœ³Έ·œÉœ³ΈΩΈΙœ΅Έ± ΈΚΈ±ΈΙ ΈΒœÉœ³ΈΙΈ±ΈΚΈ° Έ±œÄœ¨œÉœ³Έ±œÉΈΖ: 2Έ≥=(Έ€1Έ€2)=|z1 βÄ™ z2|<2Έ± βÄΔ Έ½ ΈΒΈΨΈ·œÉœâœÉΈΖ: ||z βÄ™ z1| - |z βÄ™ z2|| = 2Έ± , Έ± > 0 βÄΔ Έ†Έ±œ¹ΈΙœÉœ³Έ§ΈΫΈΒΈΙ œÖœÄΈΒœ¹Έ≤ΈΩΈΜΈ° ΈΦΈΒ ΈΒœÉœ³Έ·ΈΒœ² Έ€1 , Έ€2 œ¨œÄΈΩœÖ Έ€1 , Έ€2 ΈΒΈ·ΈΫΈ±ΈΙ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ z1 , z2 Έ±ΈΫœ³Έ·œÉœ³ΈΩΈΙœ΅Έ± ΈΚΈ±ΈΙ ΈΒœÉœ³ΈΙΈ±ΈΚΈ° Έ±œÄœ¨œÉœ³Έ±œÉΈΖ: 2Έ≥=(Έ€1Έ€2)=|z1 βÄ™ z2|>2Έ± Έ£Έ±œÉΈΙΈΚΈ≠œ² ΈΒΈΨΈΙœÉœéœÉΈΒΈΙœ² ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 19. Έ£Έ±œÉΈΙΈΚΈ≠œ² œÉœ΅Έ≠œÉΈΒΈΙœ² ΈΘΈßΈïΈΘΈ½ Έ†ΈëΈΓΈôΈΘΈΛΈëΈùΈïΈô |z βÄ™ z0| = œ¹ , œ¹ > 0 ΈöœçΈΚΈΜΈΩ ΈΦΈΒ ΈΚΈ≠ΈΫœ³œ¹ΈΩ œ³ΈΩ œÉΈΖΈΦΈΒΈ·ΈΩ Έö(x0,y0) ΈΚΈ±ΈΙ Έ±ΈΚœ³Έ·ΈΫΈ± œ¹ |z βÄ™ z0| œ¹ , œ¹ > 0 ΈöœÖΈΚΈΜΈΙΈΚœ¨ Έ¥Έ·œÉΈΚΈΩ ΈΦΈΒ ΈΚΈ≠ΈΫœ³œ¹ΈΩ œ³ΈΩ œÉΈΖΈΦΈΒΈ·ΈΩ Έö(x0,y0) ΈΚΈ±ΈΙ Έ±ΈΚœ³Έ·ΈΫΈ± œ¹ |z βÄ™ z0|< œ¹ , œ¹ > 0 ΈΛΈ± ΈΒœÉœâœ³ΈΒœ¹ΈΙΈΚΈ§ œÉΈΖΈΦΈΒΈ·Έ± œ³ΈΩœÖ ΈΚœçΈΚΈΜΈΩœÖ ΈΦΈΒ ΈΚΈ≠ΈΫœ³œ¹ΈΩ œ³ΈΩ œÉΈΖΈΦΈΒΈ·ΈΩ Έö(x0,y0) ΈΚΈ±ΈΙ Έ±ΈΚœ³Έ·ΈΫΈ± œ¹ |z βÄ™ z0|> œ¹ , œ¹ > 0 ΈΛΈ± ΈΒΈΨœâœ³ΈΒœ¹ΈΙΈΚΈ§ œÉΈΖΈΦΈΒΈ·Έ± œ³ΈΩœÖ ΈΚœçΈΚΈΜΈΩœÖ ΈΦΈΒ ΈΚΈ≠ΈΫœ³œ¹ΈΩ œ³ΈΩ œÉΈΖΈΦΈΒΈ·ΈΩ Έö(x0,y0) ΈΚΈ±ΈΙ Έ±ΈΚœ³Έ·ΈΫΈ± œ¹ |z βÄ™ z0| œ¹ , œ¹ > 0 ΈΛΈ± œÉΈΖΈΦΈΒΈ·Έ± œ³ΈΩœÖ ΈΚœçΈΚΈΜΈΩœÖ ΈΦΈΒ ΈΚΈ≠ΈΫœ³œ¹ΈΩ œ³ΈΩ œÉΈΖΈΦΈΒΈ·ΈΩ Έö(x0,y0) ΈΚΈ±ΈΙ Έ±ΈΚœ³Έ·ΈΫΈ± œ¹ ΈΚΈ±ΈΙ œ³Έ± œÉΈΖΈΦΈΒΈ·Έ± œÄΈΩœÖ Έ≤œ¹Έ·œÉΈΚΈΩΈΫœ³Έ±ΈΙ ΈΒΈΨœâœ³ΈΒœ¹ΈΙΈΚΈ§ Έ±œÖœ³ΈΩœç œ³ΈΩœÖ ΈΚœçΈΚΈΜΈΩœÖ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 20. βÄΔ ΈëΈΫ Έ≥ΈΙΈ± œ³ΈΩΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœ¨ z ΈΙœÉœ΅œçΈΒΈΙ:|z βÄ™ z0| = œ¹ , œ¹ > 0 Έ° Έ≠œ΅ΈΒΈΙœ² Έ¥ΈΒΈ·ΈΨΈΒΈΙ œ¨œ³ΈΙ ΈΖ ΈΒΈΙΈΚœ¨ΈΫΈ± œ³ΈΩœÖ z ΈΚΈΙΈΫΈΒΈ·œ³Έ±ΈΙ œÉΈΒ ΈΚœçΈΚΈΜΈΩ ΈΚΈ±ΈΙ œÉΈΩœÖ ΈΕΈΖœ³ΈΩœçΈΫ ΈΫΈ± Έ≤œ¹ΈΒΈΙœ² œ³ΈΖ ΈΦΈ≠Έ≥ΈΙœÉœ³ΈΖ ΈΚΈ±ΈΙ œ³ΈΖΈΫ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΖ œ³ΈΙΈΦΈ° œ³ΈΩœÖ |z| , œ³œ¨œ³ΈΒ: βÄΔ max|z| = (KO) + œ¹ βÄΔ min|z| = (KO) βÄ™ œ¹ βÄΔ œ¨œÄΈΩœÖ Έö ΈΖ ΈΒΈΙΈΚœ¨ΈΫΈ± œ³ΈΩœÖ z0 ΈΚΈ±ΈΙ œ¹ ΈΖ Έ±ΈΚœ³Έ·ΈΫΈ± œ³ΈΩœÖ ΈΚœçΈΚΈΜΈΩœÖ ΈΦΈΒ ΈΚΈ≠ΈΫœ³œ¹ΈΩ œ³ΈΩ Έö . βÄΔ Έ™ΈΙΈ± ΈΫΈ± Έ≤œ¹ΈΒΈΙœ² œ³ΈΩœÖœ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœçœ² ΈΦΈΒ œ³ΈΩ ΈΦΈ≠Έ≥ΈΙœÉœ³ΈΩ ΈΚΈ±ΈΙ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΩ ΈΦΈ≠œ³œ¹ΈΩ, ΈΜœçΈΫΈΒΈΙœ² œ³ΈΩ œÉœçœÉœ³ΈΖΈΦΈ± œ³œâΈΫ ΈΒΈΨΈΙœÉœéœÉΈΒœâΈΫ œ³ΈΖœ² ΈΒœÖΈΗΈΒΈ·Έ±œ² ΈüΈö ΈΚΈ±ΈΙ œ³ΈΩœÖ ΈΚœçΈΚΈΜΈΩœÖ Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ Έ€Έ≠Έ≥ΈΙœÉœ³ΈΖ ΈΚΈ±ΈΙ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΖ œ³ΈΙΈΦΈ° ΈΦΈ≠œ³œ¹ΈΩœÖ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç Έü Έë Έ£ Έö ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 21. βÄΔ ΈëΈΫ ΈΖ ΈΒΈΙΈΚœ¨ΈΫΈ± œ³ΈΩœÖ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç z ΈΨΈ≠œ¹ΈΒΈΙœ² œ¨œ³ΈΙ ΈΚΈΙΈΫΈΒΈ·œ³Έ±ΈΙ œÉΈΒ ΈΒœÖΈΗΈΒΈ·Έ± (ΈΒ), œ³œ¨œ³ΈΒ ΈΩ z Έ≠œ΅ΈΒΈΙ ΈΦœ¨ΈΫΈΩ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΩ ΈΦΈ≠œ³œ¹ΈΩ. βÄΔ Έ™ΈΙΈ± ΈΫΈ± Έ≤œ¹ΈΒΈΙœ² œ³ΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœ¨ ΈΦΈΒ œ³ΈΩ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΩ ΈΦΈ≠œ³œ¹ΈΩ, œÜΈ≠œ¹ΈΫΈΒΈΙœ² ΈΚΈ§ΈΗΈΒœ³ΈΖ Έ±œÄœ¨ œ³ΈΖΈΫ Έ±œ¹œ΅Έ° œ³œâΈΫ Έ±ΈΨœ¨ΈΫœâΈΫ œÉœ³ΈΖΈΫ ΈΒœÖΈΗΈΒΈ·Έ± (ΈΒ) ΈΚΈ±ΈΙ Έ≤œ¹Έ·œÉΈΚΈΒΈΙœ² œ³ΈΩ œÉΈΖΈΦΈΒΈ·ΈΩ œ³ΈΩΈΦΈ°œ² œ³œâΈΫ Έ¥œçΈΩ ΈΒœÖΈΗΈΒΈΙœéΈΫ. βÄΔ min|z|= d(O,ΈΒ) βÄΔ Έ™ΈΙΈ± ΈΒœÜΈ±œ¹ΈΦΈΩΈ≥Έ°: βÄΔ ΈΒœÜΈ±œ¹ΈΦΈΩΈ≥Έ° 2 œÉΈΒΈΜ.99 , Έë7 œÉΈΒΈΜ.101 , Έ£8 œÉΈΒΈΜ.102 , Έ™3 œÉΈΒΈΜ. 123 œÉœ΅ΈΩΈΜΈΙΈΚΈΩœç Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ Έ€Έ≠Έ≥ΈΙœÉœ³ΈΖ ΈΚΈ±ΈΙ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΖ œ³ΈΙΈΦΈ° ΈΦΈ≠œ³œ¹ΈΩœÖ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç Έü ΈΒ ΈΕ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 22. βÄΔ ΈëΈΫ ΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœ¨œ² z ΈΦΈΒ ΈΒΈΙΈΚœ¨ΈΫΈ± Έ€ ΈΚΈΙΈΫΈΒΈ·œ³Έ±ΈΙ œÉΈΒ ΈΚœçΈΚΈΜΈΩ (Έö,œ¹) ΈΚΈ±ΈΙ ΈΩ w ΈΦΈΒ ΈΒΈΙΈΚœ¨ΈΫΈ± Έù ΈΒΈ·ΈΫΈ±ΈΙ œÉœ³Έ±ΈΗΈΒœ¹œ¨œ² ,œ³œ¨œ³ΈΒ: βÄΔ max |z βÄ™ w|=(NB)=(NΈö)+œ¹ ΈΚΈ±ΈΙ βÄΔ min |z βÄ™ w|=(NA)=|(NK)-œ¹| βÄΔ ΈëΈΫ ΈΖ ΈΒΈΙΈΚœ¨ΈΫΈ± œ³ΈΩœÖ w Έ±ΈΫΈ°ΈΚΈΒΈΙ ΈΚΈ±ΈΙ Έ±œÖœ³Έ° œÉœ³ΈΩΈΫ ΈΚœçΈΚΈΜΈΩ (Έö , œ¹) œ³œ¨œ³ΈΒ: βÄΔ max |z βÄ™ w|=(NB)=2œ¹ ΈΚΈ±ΈΙ βÄΔ min |z βÄ™ w|=0 Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ Έ€Έ≠Έ≥ΈΙœÉœ³ΈΖ ΈΚΈ±ΈΙ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΖ œ³ΈΙΈΦΈ° ΈΦΈ≠œ³œ¹ΈΩœÖ Έ¥ΈΙΈ±œÜΈΩœ¹Έ§œ² Έ¥œçΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ O K y x N B A ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 23. βÄΔ ΈëΈΫ ΈΖ ΈΒΈΙΈΚœ¨ΈΫΈ± Έ€ œ³ΈΩœÖ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç z ΈΚΈΙΈΫΈΒΈ·œ³Έ±ΈΙ œÉΈΒ ΈΒœÖΈΗΈΒΈ·Έ± (ΈΒ) ΈΚΈ±ΈΙ Έù ΈΒΈ·ΈΫΈ±ΈΙ ΈΖ ΈΒΈΙΈΚœ¨ΈΫΈ± œ³ΈΩœÖ w,œ³œ¨œ³ΈΒ: βÄΔ max |z βÄ™ w| Έ¥ΈΒΈΫ œÖœÄΈ§œ¹œ΅ΈΒΈΙ ΈΚΈ±ΈΙ βÄΔ min |z βÄ™ w|= d(N,ΈΒ) Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ Έ€Έ≠Έ≥ΈΙœÉœ³ΈΖ ΈΚΈ±ΈΙ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΖ œ³ΈΙΈΦΈ° ΈΦΈ≠œ³œ¹ΈΩœÖ Έ¥ΈΙΈ±œÜΈΩœ¹Έ§œ² Έ¥œçΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ O y x N ΈΒ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 24. Έ‰œÖΈΦΈ§ΈΦΈ±ΈΙ ΈëœÄœ¨œÉœ³Έ±œÉΈΖ œÉΈΖΈΦΈΒΈ·ΈΩœÖ Έ±œÄœ¨ ΈΒœÖΈΗΈΒΈ·Έ± ΈëΈΫ Έ€1(x1,y1) ΈΚΈ±ΈΙ ΈΒ:Έëx+By+Έ™ = 0 œ³œ¨œ³ΈΒ : d(M1 , ΈΒ) = πùö®πù£ô πùüè+πùö©πù£ö πùüè+πùöΣ πùö® πùüê+πùö© πùüê ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 25. Έ‰œÖΈΦΈ§ΈΦΈ±ΈΙ ΈöœçΈΚΈΜΈΩœ² ΈöΈ≠ΈΫœ³œ¹ΈΩ ΈΚœçΈΚΈΜΈΩœÖ ΈïΈΨΈ·œÉœâœÉΈΖ ΈΚœçΈΚΈΜΈΩœÖ O(0 , 0) C: x2 + y2 = œ¹2 Έö(x0 , y0) C: (x βÄ™ x0)2 + (y βÄ™ y0)2 = œ¹2 πùö± β࣠πùö® πùüê , β࣠πùö© πùüê C: x2 + y2 + Ax + By + Έ™= 0 ΈΦΈΒ Έë2 + Έ£2 βÄ™ 4Έ™ > 0 ΈëΈΚœ³Έ·ΈΫΈ± : πùùÜ = πùö® πùüê+πùö© πùüêβà£πùü£πùöΣ πùüê ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 26. βÄΔ ΈëΈΫ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ z , w ΈΚΈΙΈΫΈΩœçΈΫœ³Έ±ΈΙ œÉΈΒ ΈΚœçΈΚΈΜΈΩ (Έö,œ¹), ΈΦΈΒ z β↠w, œ³œ¨œ³ΈΒ: βÄΔ max |z βÄ™ w|= Έ€Έù = 2œ¹. βÄΔ min |z βÄ™ w|Έ¥ΈΒΈΫ œÖœÄΈ§œ¹œ΅ΈΒΈΙ Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ Έ€Έ≠Έ≥ΈΙœÉœ³ΈΖ ΈΚΈ±ΈΙ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΖ œ³ΈΙΈΦΈ° ΈΦΈ≠œ³œ¹ΈΩœÖ Έ¥ΈΙΈ±œÜΈΩœ¹Έ§œ² Έ¥œçΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ O K y x Έ€ Έù ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 27. βÄΔ ΈëΈΫ ΈΖ ΈΒΈΙΈΚœ¨ΈΫΈ± œ³ΈΩœÖ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç z ΈΚΈΙΈΫΈΒΈ·œ³Έ±ΈΙ œÉΈΒ ΈΚœçΈΚΈΜΈΩ (Έö,œ¹) ΈΚΈ±ΈΙ œ³ΈΩœÖ w œÉΈΒ ΈΒœÖΈΗΈΒΈ·Έ± (ΈΒ) ,œ³œ¨œ³ΈΒ βÄΔ max |z βÄ™ w|Έ¥ΈΒΈΫ œÖœÄΈ§œ¹œ΅ΈΒΈΙ βÄΔ min |z βÄ™ w|= |d(K , ΈΒ) βÄ™ œ¹| Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ Έ€Έ≠Έ≥ΈΙœÉœ³ΈΖ ΈΚΈ±ΈΙ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΖ œ³ΈΙΈΦΈ° ΈΦΈ≠œ³œ¹ΈΩœÖ Έ¥ΈΙΈ±œÜΈΩœ¹Έ§œ² Έ¥œçΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ O K y x ΈΒ ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 28. βÄΔ ΈëΈΫ ΈΖ ΈΒΈΙΈΚœ¨ΈΫΈ± œ³ΈΩœÖ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç z ΈΚΈΙΈΫΈΒΈ·œ³Έ±ΈΙ œÉΈΒ ΈΚœçΈΚΈΜΈΩ (Έö , œ¹) ΈΚΈ±ΈΙ œ³ΈΩœÖ w œÉΈΒ ΈΚœçΈΚΈΜΈΩ (Έ¦,R) ΈΚΈ±ΈΙ ΈΩΈΙ ΈΚœçΈΚΈΜΈΩΈΙ Έ¥ΈΒΈΫ Έ≠œ΅ΈΩœÖΈΫ ΈΚΈΩΈΙΈΫœ¨ œÉΈΖΈΦΈΒΈ·ΈΩ (œÉœ΅Έ°ΈΦΈ± 1), œ³œ¨œ³ΈΒ βÄΔ max |z βÄ™ w|= (ΈöΈ¦) + œ¹ + R βÄΔ min |z βÄ™ w|= |(ΈöΈ¦)βÄ™ œ¹ - R| βÄΔ ΈëΈΫ ΈΩΈΙ ΈΚœçΈΚΈΜΈΩΈΙ Έ≠œ΅ΈΩœÖΈΫ ΈΚΈΩΈΙΈΫœ¨ œÉΈΖΈΦΈΒΈ·ΈΩ (œÉœ΅Έ°ΈΦΈ± 2) œ³œ¨œ³ΈΒ min|z βÄ™ w|= 0. Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ Έ€Έ≠Έ≥ΈΙœÉœ³ΈΖ ΈΚΈ±ΈΙ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΖ œ³ΈΙΈΦΈ° ΈΦΈ≠œ³œ¹ΈΩœÖ Έ¥ΈΙΈ±œÜΈΩœ¹Έ§œ² Έ¥œçΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ O K y x Έë Έ£ Έ™ Έî Έ¦ œÉœ΅Έ°ΈΦΈ± 1 œÉœ΅Έ°ΈΦΈ± 2 y O K Έ¦ x x K Έ¦ O y ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 29. βÄΔ ΈëΈΫ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ z , w ΈΦΈΒ z β↠w ΈΚΈΙΈΫΈΩœçΈΫœ³Έ±ΈΙ œÉΈΒ Έ≠ΈΜΈΜΈΒΈΙœàΈΖ, œ³œ¨œ³ΈΒ βÄΔ max |z βÄ™ w|= 2Έ± , Έ¥ΈΖΈΜΈ±Έ¥Έ° ΈΩ ΈΦΈΒΈ≥Έ§ΈΜΈΩœ² Έ§ΈΨΈΩΈΫΈ±œ². βÄΔ Έ™ΈΙΈ± ΈΒΈΨΈ§œÉΈΚΈΖœÉΈΖ Έ¥ΈΒœ²: ΈïœÜΈ±œ¹ΈΦΈΩΈ≥Έ° 2 œÉΈΒΈΜ.99 œÉœ΅ΈΩΈΜΈΙΈΚΈΩœç, Έ±œÉΈΚΈ°œÉΈΒΈΙœ² Έë7 œÉΈΒΈΜ.101, Έ£8 œÉΈΒΈΜ.102 ΈΚΈ±ΈΙ Έ™3 œÉΈΒΈΜ.123 œÉœ΅ΈΩΈΜΈΙΈΚΈΩœç Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ Έ€Έ≠Έ≥ΈΙœÉœ³ΈΖ ΈΚΈ±ΈΙ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΖ œ³ΈΙΈΦΈ° ΈΦΈ≠œ³œ¹ΈΩœÖ Έ¥ΈΙΈ±œÜΈΩœ¹Έ§œ² Έ¥œçΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ O y xΈëΈ³ Έë ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 30. βÄΔ Έ¥ΈΖΈΜΈ±Έ¥Έ° Έ±ΈΫ ΈΦΈΙΈ± œÄΈ±œ¹Έ§œÉœ³Έ±œÉΈΖ ΈΦΈΒ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœçœ² ΈΒΈ·ΈΫΈ±ΈΙ Έ·œÉΈΖ ΈΦΈΒ ΈΦΈΖΈ¥Έ≠ΈΫ ,œ³œ¨œ³ΈΒ ΈΚΈ±ΈΙ ΈΖ œÉœÖΈΕœÖΈ≥Έ°œ² œÄΈ±œ¹Έ§œÉœ³Έ±œÉΈΖ Έ±œÖœ³Έ°œ² ΈΒΈ·ΈΫΈ±ΈΙ Έ·œÉΈΖ ΈΦΈΒ ΈΦΈΖΈ¥Έ≠ΈΫ. βÄΔ Έ†Έ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ± βÄΔ ΈëΈΫ z1 + z2 = z3 ΈΚΈ±ΈΙ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ Έ±œÖœ³œéΈΫ ΈΚΈΙΈΫΈΩœçΈΫœ³Έ±ΈΙ œÉΈΒ ΈΚœçΈΚΈΜΈΩ ΈΦΈΒ ΈΚΈ≠ΈΫœ³œ¹ΈΩ œ³ΈΩ Έü(0,0) ΈΚΈ±ΈΙ Έ±ΈΚœ³Έ·ΈΫΈ± 2, ΈΫΈ± Έ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ: z2z3 + z1z3 = z1z2 Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ ΈëΈΫ πù£΅(πù£¦ , πù£‰) = 0 œ³œ¨œ³ΈΒ ΈΚΈ±ΈΙ πù£΅(πù£¦ , πù£‰) = 0 ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
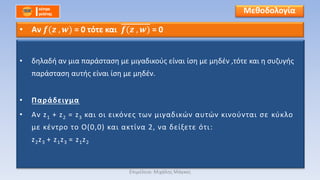
- 31. βÄΔ Έ¥ΈΖΈΜΈ±Έ¥Έ° ΈΦΈΙΈ± œÄΈ±œ¹Έ§œÉœ³Έ±œÉΈΖ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ ΈΚΈ±ΈΙ ΈΖ œÉœÖΈΕœÖΈ≥Έ°œ² œ³ΈΖœ² Έ≠œ΅ΈΩœÖΈΫ Έ·œÉΈ± ΈΦΈ≠œ³œ¹Έ±. βÄΔ Έ†Έ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ± βÄΔ ΈëΈΫ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ z1 , z2 , z3 ΈΚΈΙΈΫΈΩœçΈΫœ³Έ±ΈΙ œÉΈΒ ΈΚœçΈΚΈΜΈΩ ΈΦΈΒ ΈΚΈ≠ΈΫœ³œ¹ΈΩ œ³ΈΩ Έü(0,0) ΈΚΈ±ΈΙ Έ±ΈΚœ³Έ·ΈΫΈ± 2, ΈΫΈ± Έ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ: πùëß1 + 2πùëß2 β࣠3πùëß3 = 1 2 πùëß2 πùëß3 + 2πùëß1 πùëß3 β࣠3πùëß1 πùëß2 Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ |πù£΅ πù£¦ , πù£‰ | = |πù£΅(πù£¦ , πù£‰)| ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 32. βÄΔ Έ€ΈΒœ³Έ§ œÖœàœéΈΫΈΩœÖΈΦΈΒ œÉœ³ΈΩ œ³ΈΒœ³œ¹Έ§Έ≥œâΈΫΈΩ œ³Έ± Έ¥œçΈΩ ΈΦΈ≠ΈΜΈΖ ΈΚΈ±ΈΙ œ΅œ¹ΈΖœÉΈΙΈΦΈΩœÄΈΩΈΙΈΩœçΈΦΈΒ œ³ΈΖΈΫ ΈΙΈ¥ΈΙœ¨œ³ΈΖœ³Έ± |z|2 = πù£¦πù£¦ βÄΔ Έ™ΈΙΈ± œÄΈ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ±: βÄΔ 1. ΈëΈΫ z , w C ΈΚΈ±ΈΙ zΈΫ = w |zΈΫ| = |w| |z|= | πù£‰|πùù² βÄΔ 2. ΈëΈΫ z , w C ΈΚΈ±ΈΙ zΈΫ = wΈΫ |z|ΈΫ = |w|ΈΫ βÄΔ |z| = |w| |z|2 = |w|2 πù£¦πù£¦ = πù£‰ πù£‰ βÄΔ 3. Έ™ΈΒΈΫΈΙΈΚΈ§ [f(z)]ΈΫ = [g(z)]ΈΫ | f(z)|ΈΫ = |g(z)|ΈΫ |f(z)|=|g(z)| βÄΔ |f(z)|2 = |g(z)|2 πù£΅(πù£¦)πù£΅(πù£¦) πù£à( πù£¦)πù£à(πù£¦) Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ± βÄΔ Έ¨œ³Έ±ΈΫ Έ≠œ΅ΈΩœÖΈΦΈΒ ΈΦΈΙΈ± ΈΙœÉœ¨œ³ΈΖœ³Έ± ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ, œÉΈΒ œÄΈΩΈΜΈΜΈ≠œ² œÄΈΒœ¹ΈΙœÄœ³œéœÉΈΒΈΙœ² œ΅œ¹ΈΖœÉΈΙΈΦΈΩœÄΈΩΈΙΈΩœçΈΦΈΒ œ¨œ³ΈΙ ΈΚΈ±ΈΙ œ³Έ± ΈΦΈ≠œ³œ¹Έ± œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ ΈΒΈ·ΈΫΈ±ΈΙ Έ·œÉΈ± (œ΅œâœ¹Έ·œ² ΈΫΈ± ΈΙœÉœ΅œçΈΒΈΙ œ³ΈΩ Έ±ΈΫœ³Έ·œÉœ³œ¹ΈΩœÜΈΩ) ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 33. βÄΔ 1. Έ§œÉΈΚΈΖœÉΈΖ Έ™6 œÉΈΒΈΜΈ·Έ¥Έ± 123 œÉœ΅ΈΩΈΜΈΙΈΚΈΩœç Έ≤ΈΙΈ≤ΈΜΈ·ΈΩœÖ βÄΔ 2. ΈëΈΫ (1 + iz)ΈΫ = (1 βÄ™ iz)ΈΫ ΈΫΈ± Έ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ z R. βÄΔ ΈΘΈΒ œ³œ¹Έ·Έ≥œâΈΫΈΩ, Έ±ΈΫ Έë,Έ£,Έ™ ΈΒΈ·ΈΫΈ±ΈΙ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ z , w , u, œ³œ¨œ³ΈΒ: βÄΔ Έ±. ΈëΈ£Έ™ ΈΙœÉœ¨œÄΈΜΈΒœÖœ¹ΈΩ ΈëΈ£ = Έ£Έ™ = Έ™Έë |z-w|=|u-w|=|z-u| βÄΔ Έ≤. ΈëΈ£Έ™ ΈΙœÉΈΩœÉΈΚΈΒΈΜΈ≠œ² ΈΦΈΒ Έ≤Έ§œÉΈΖ Έ£Έ™ ΈëΈ£=ΈëΈ™ |z-w|=|z-u| βÄΔ Έ≥. ΈëΈ£Έ™ ΈΩœ¹ΈΗΈΩΈ≥œéΈΫΈΙΈΩ ΈΦΈΒ πùö®=900 ΈëΈ£2 + ΈëΈ™2 = Έ£Έ™2 |z-w|2 + |z-u|2 = |w-u|2 βÄΔ Έ†Έ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ±: βÄΔ ΈëΈΫ Έ≥ΈΙΈ± œ³ΈΩœÖœ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœçœ² z1 , z2 , z3 ΈΙœÉœ΅œçΈΩœÖΈΫ ΈΩΈΙ œÉœ΅Έ≠œÉΈΒΈΙœ²: z1 + z2 + z3 = 0 ΈΚΈ±ΈΙ |z1|=|z2|=|z3|=1 , ΈΫΈ± Έ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ z1 , z2 , z3 ΈΒΈ·ΈΫΈ±ΈΙ ΈΚΈΩœ¹œÖœÜΈ≠œ² ΈΙœÉΈΩœÄΈΜΈΒœçœ¹ΈΩœÖ œ³œ¹ΈΙΈ≥œéΈΫΈΩœÖ ΈΒΈ≥Έ≥ΈΒΈ≥œ¹Έ±ΈΦΈΦΈ≠ΈΫΈΩœÖ œÉΈΒ ΈΚœçΈΚΈΜΈΩ Έ±ΈΚœ³Έ·ΈΫΈ±œ² 1 . Έ€ΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩΈ· ΈΚΈ±ΈΙ œ³œ¹Έ·Έ≥œâΈΫΈΩΈ†Έ±œ¹Έ±Έ¥ΈΒΈ·Έ≥ΈΦΈ±œ³Έ± ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 34. Έ™ΈΒœâΈΦΈΒœ³œ¹ΈΙΈΚΈΩΈ· œ³œ¨œÄΈΩΈΙ ΈΘΈΒ Έ±œÉΈΚΈ°œÉΈΒΈΙœ² œÄΈΩœÖ ΈΦΈ±œ² ΈΕΈΖœ³ΈΩœçΈΫ ΈΫΈ± Έ≤œ¹ΈΩœçΈΦΈΒ œ³ΈΩ Έ≥ΈΒœâΈΦΈΒœ³œ¹ΈΙΈΚœ¨ œ³œ¨œÄΈΩ œ³œâΈΫ ΈΒΈΙΈΚœ¨ΈΫœâΈΫ ΈΒΈΫœ¨œ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœç Έ±œ¹ΈΙΈΗΈΦΈΩœç z ΈΩ ΈΩœÄΈΩΈ·ΈΩœ² ΈΙΈΚΈ±ΈΫΈΩœÄΈΩΈΙΈΒΈ· ΈΦΈΙΈ± œÉœ΅Έ≠œÉΈΖ Έ° œÉœÖΈΫΈ¥Έ≠ΈΒœ³Έ±ΈΙ ΈΦΈΒ ΈΦΈΙΈ± œÉœ΅Έ≠œÉΈΖ ΈΦΈΒ Έ≠ΈΫΈ± Έ§ΈΜΈΜΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœ¨ w 1. Έ†œ¹ΈΩœÉœÄΈ±ΈΗœé ΈΫΈ± ΈΚΈ±œ³Έ±ΈΜΈ°ΈΨœâ œÉΈΒ ΈΦΈΙΈ± œÉœ΅Έ≠œÉΈΖ œ³ΈΖœ² ΈΦΈΩœ¹œÜΈ°œ²: |z-z0|=œ¹, œ¹>0 Έ° |z-z1|=|z-z2| ΈΚΈ±ΈΙ ΈΒœÄΈΩΈΦΈ≠ΈΫœâœ² Έ≥ΈΫœâœ¹Έ·ΈΕœâ œÉΈΒ œÄΈΩΈΙΈ± Έ≥œ¹Έ±ΈΦΈΦΈ° ΈΚΈΙΈΫΈΩœçΈΫœ³Έ±ΈΙ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³ΈΩœÖ z. Έ†Έ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ± ΈëΈΫ Έ≥ΈΙΈ± œ³ΈΩœÖœ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœçœ² z ΈΚΈ±ΈΙ w ΈΙœÉœ΅œçΈΩœÖΈΫ |z|=2 ΈΚΈ±ΈΙ w=(- πùüë+i)iz, œ³œ¨œ³ΈΒ ΈΫΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ œ³ΈΩ Έ≥œ¹Έ±ΈΦΈΦΈ° œÉœ³ΈΖΈΫ ΈΩœÄΈΩΈ·Έ± Έ±ΈΫΈ°ΈΚΈΩœÖΈΫ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ w. 2. ΈëΈΫ Έ¥ΈΒΈΫ ΈΦœÄΈΩœ¹ΈΒΈ· ΈΫΈ± œÉœÖΈΦΈ≤ΈΒΈ· œ³ΈΩ 1. œ³œ¨œ³ΈΒ ΈΗΈ≠œ³ΈΩœÖΈΦΈΒ œÉœ³ΈΖ œÉœ΅Έ≠œÉΈΖ ΈΦΈ±œ² œ¨œÄΈΩœÖ z = x+yi œ³ΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœ¨ œ³ΈΩœÖ ΈΩœÄΈΩΈ·ΈΩœÖ œ³ΈΩ Έ≥ΈΒœâΈΦΈΒœ³œ¹ΈΙΈΚœ¨ œ³œ¨œÄΈΩ œ³œâΈΫ ΈΒΈΙΈΚœ¨ΈΫœâΈΫ ΈΗΈ≠ΈΜΈΩœÖΈΦΈΒ ΈΫΈ± Έ≤œ¹ΈΩœçΈΦΈΒ ΈΚΈ±ΈΙ w= ΈΚ+ΈΜi œ³ΈΩ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœ¨ Έ≥ΈΙΈ± œ³ΈΩΈΫ ΈΩœÄΈΩΈ·ΈΩ œÉœÖΈΫΈ°ΈΗœâœ² Έ≥ΈΫœâœ¹Έ·ΈΕΈΩœÖΈΦΈΒ œÉΈΒ œÄΈΩΈΙΈ± Έ≥œ¹Έ±ΈΦΈΦΈ° Έ±ΈΫΈ°ΈΚΈΩœÖΈΫ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³ΈΩœÖ, Έ§œ¹Έ± Έ≥ΈΫœâœ¹Έ·ΈΕΈΩœÖΈΦΈΒ ΈΦΈΙΈ± œÉœ΅Έ≠œÉΈΖ œÄΈΩœÖ ΈΙΈΚΈ±ΈΫΈΩœÄΈΩΈΙΈΩœçΈΫ œ³Έ± ΈΚ ΈΚΈ±ΈΙ ΈΜ. ΈΘœ³œ¨œ΅ΈΩœ² ΈΦΈ±œ² ΈΒΈ·ΈΫΈ±ΈΙ ΈΫΈ± ΈΒΈΚœÜœ¹Έ§œÉΈΩœÖΈΦΈΒ œ³Έ± ΈΚ , ΈΜ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒΈΙ œ³œâΈΫ x ΈΚΈ±ΈΙ y ΈΚΈ±ΈΙ ΈΫΈ± œ³Έ± Έ±ΈΫœ³ΈΙΈΚΈ±œ³Έ±œÉœ³Έ°œÉΈΩœÖΈΦΈΒ œÉœ³ΈΖ œÉœ΅Έ≠œÉΈΖ œÄΈΩœÖ ΈΙΈΚΈ±ΈΫΈΩœÄΈΩΈΙΈΩœçΈΫ œ³Έ± ΈΚ ΈΚΈ±ΈΙ ΈΜ. Έ†Έ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ± ΈëΈΫ Έ≥ΈΙΈ± œ³ΈΩœÖœ² ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚΈΩœçœ² z ΈΚΈ±ΈΙ w ΈΙœÉœ΅œçΈΩœÖΈΫ |z|=2 ΈΚΈ±ΈΙ w=2z+πù£¦ , œ³œ¨œ³ΈΒ ΈΫΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ œ³ΈΖ Έ≥œ¹Έ±ΈΦΈΦΈ° œÉœ³ΈΖΈΫ ΈΩœÄΈΩΈ·Έ± Έ±ΈΫΈ°ΈΚΈΩœÖΈΫ ΈΩΈΙ ΈΒΈΙΈΚœ¨ΈΫΈΒœ² œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ w. ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²
- 35. βÄΔ ΈïΈΞΈßΈüΈ€ΈëΈΘΈΛΈï ΈΘΈï ΈüΈ¦ΈïΈΘ ΈöΈëΈô ΈüΈ¦ΈüΈΞΈΘ ΈïΈ†ΈôΈΛΈΞΈßΈôΈë!! βÄΔ ΈùΈë ΈîΈôΈëΈ£ΈëΈΘΈïΈΛΈï ΈûΈëΈùΈë ΈΛΈ½ Έ‰ΈïΈ©ΈΓΈôΈë ΈöΈëΈô ΈùΈë ¬ΪΈΠΈΓΈïΈΘΈöΈëΈΓΈïΈΛΈï¬Μ ΈΛΈΓΈüΈ†ΈüΈΞΈΘ Έ¦ΈΞΈΘΈ½ΈΘ ΈëΈΘΈöΈ½ΈΘΈïΈ©Έù. βÄΔ ΈùΈë ΈïΈßΈïΈΛΈï Έ®ΈΞΈßΈΓΈëΈôΈ€ΈôΈë ΈöΈëΈô ΈùΈë Έ†ΈëΈΓΈëΈΛΈ½ΈΓΈïΈôΈΛΈï ΈöΈëΈ¦Έë ΈΛΈë ΈîΈïΈîΈüΈ€ΈïΈùΈë. βÄΔ ΈöΈëΈ‰ΈëΈΓΈü Έ€ΈΞΈëΈ¦Έü Έ†ΈëΈùΈ© ΈëΈ†Έ³ ΈüΈ¦Έë! Έ½ ΈΒœÄΈΙœÄΈΩΈΜΈ±ΈΙœ¨œ³ΈΖœ³Έ± ΈΚΈ±ΈΙ ΈΖ Έ≤ΈΙΈ±œÉœçΈΫΈΖ Έ¥ΈΒΈΫ œÉΈ±œ² œ³Έ±ΈΙœ¹ΈΙΈ§ΈΕΈΒΈΙ! βÄΔ ΈùΈë ΈΠΈΞΈ™ΈïΈΛΈï ΈΛΈïΈ¦ΈïΈΞΈΛΈëΈôΈüΈô ΈëΈ†Έü ΈΛΈ½Έù ΈëΈôΈ‰ΈüΈΞΈΘΈë! βÄΔ ΈùΈ± Έ≠œ΅ΈΒœ³ΈΒ ΈΒΈΦœÄΈΙœÉœ³ΈΩœÉœçΈΫΈΖ œÉœ³ΈΩΈΫ ΈΒΈ±œÖœ³œ¨ œÉΈ±œ² ΈΚΈ±ΈΙ œÉœ³ΈΖ Έ¥ΈΙΈ±Έ·œÉΈΗΈΖœÉΈ° œÉΈ±œ²! βÄΔ ΈΘΈëΈΘ ΈïΈΞΈßΈüΈ€ΈëΈΘΈΛΈï ΈùΈë Έ£Έ™ΈïΈôΈΛΈï ¬ΪΈùΈôΈöΈ½ΈΛΈïΈΘ¬Μ ΈöΈëΈô ΈëΈ†Έü ΈëΈΞΈΛΈ½Έù ΈΛΈ½ ΈîΈüΈöΈôΈ€ΈëΈΘΈôΈë! ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²


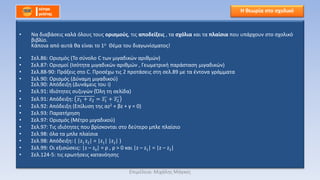



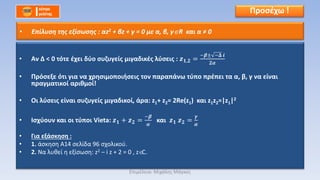


















![βÄΔ Έ€ΈΒœ³Έ§ œÖœàœéΈΫΈΩœÖΈΦΈΒ œÉœ³ΈΩ œ³ΈΒœ³œ¹Έ§Έ≥œâΈΫΈΩ œ³Έ± Έ¥œçΈΩ ΈΦΈ≠ΈΜΈΖ ΈΚΈ±ΈΙ œ΅œ¹ΈΖœÉΈΙΈΦΈΩœÄΈΩΈΙΈΩœçΈΦΈΒ œ³ΈΖΈΫ ΈΙΈ¥ΈΙœ¨œ³ΈΖœ³Έ±
|z|2 = πù£¦πù£¦
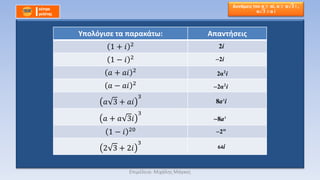
βÄΔ Έ™ΈΙΈ± œÄΈ±œ¹Έ§Έ¥ΈΒΈΙΈ≥ΈΦΈ±:
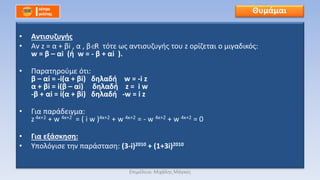
βÄΔ 1. ΈëΈΫ z , w C ΈΚΈ±ΈΙ zΈΫ = w |zΈΫ| = |w| |z|= | πù£‰|πùù²
βÄΔ 2. ΈëΈΫ z , w C ΈΚΈ±ΈΙ zΈΫ = wΈΫ |z|ΈΫ = |w|ΈΫ
βÄΔ |z| = |w| |z|2 = |w|2 πù£¦πù£¦ = πù£‰ πù£‰
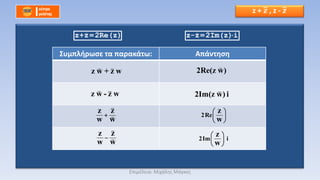
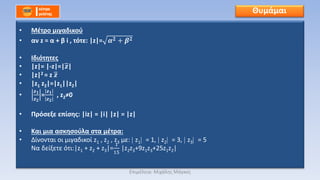
βÄΔ 3. Έ™ΈΒΈΫΈΙΈΚΈ§ [f(z)]ΈΫ = [g(z)]ΈΫ | f(z)|ΈΫ = |g(z)|ΈΫ |f(z)|=|g(z)|
βÄΔ |f(z)|2 = |g(z)|2 πù£΅(πù£¦)πù£΅(πù£¦) πù£à( πù£¦)πù£à(πù£¦)
Έ€ΈΒΈΗΈΩΈ¥ΈΩΈΜΈΩΈ≥Έ·Έ±
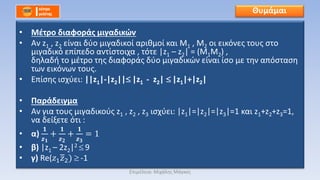
βÄΔ Έ¨œ³Έ±ΈΫ Έ≠œ΅ΈΩœÖΈΦΈΒ ΈΦΈΙΈ± ΈΙœÉœ¨œ³ΈΖœ³Έ± ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ, œÉΈΒ œÄΈΩΈΜΈΜΈ≠œ² œÄΈΒœ¹ΈΙœÄœ³œéœÉΈΒΈΙœ² œ΅œ¹ΈΖœÉΈΙΈΦΈΩœÄΈΩΈΙΈΩœçΈΦΈΒ œ¨œ³ΈΙ ΈΚΈ±ΈΙ œ³Έ±
ΈΦΈ≠œ³œ¹Έ± œ³œâΈΫ ΈΦΈΙΈ≥Έ±Έ¥ΈΙΈΚœéΈΫ ΈΒΈ·ΈΫΈ±ΈΙ Έ·œÉΈ± (œ΅œâœ¹Έ·œ² ΈΫΈ± ΈΙœÉœ΅œçΈΒΈΙ œ³ΈΩ Έ±ΈΫœ³Έ·œÉœ³œ¹ΈΩœÜΈΩ)
ΈïœÄΈΙΈΦΈ≠ΈΜΈΒΈΙΈ±: Έ€ΈΙœ΅Έ§ΈΜΈΖœ² Έ€Έ§Έ≥ΈΚΈΩœ²](https://image.slidesharecdn.com/random-140502042056-phpapp01/85/-32-320.jpg)