NDT-TKU

Apr 8, 2017Download as PPTX, PDF2 likes3,861 views

NDT-TKU is an improved 3D Normal Distributions Transform method for mobile robotic mapping proposed by Takeuchi from Nagoya University. It uses a two-stage converging process where the voxel size is adjusted based on point density during registration. This allows for higher accuracy while reducing computation compared to a single voxel size. The key aspects of NDT-TKU include overlapping voxels, trilinear interpolation, and dividing the registration into converging and adjustment states.

What is ndt_tku
?A 3-D Scan Matching using Improved 3-D Normal Distributions
Transform for Mobile Robotic Mapping
?名古屋大學竹內先生(TAKEUCHI)提出的 NDT 優化版
?Autoware/ros/src/computing/perception/localization/packages/n
dt_localizer/nodes/ndt_matching_tku/

Why is ndt_tku
?是指導教授提出的
?PCL 的 cuda 化極度麻煩，工程師表示不如自幹一套，然後
cuda 化

Outline ndt_tku
? ND
? NDT in slam
? NDT_TKU

Normal Distribution
? 正態分佈 - 是一個在數學、物理及工程等領域都非常重要的機率分佈，由於這個分布函數具有很多
非常漂亮的性質.使得其在諸多涉及統計科學離散科學等領域的許多方面都有著重大的影響力.
? 符合
? 台灣收入分佈
? 不符合
? 骰子各面機率，我跟連家人的收入分佈。

Normal Distribution Transform
Subdivide the space occupied by the scan into a grid of cells.
A PDF is computed for each cell, based on the point distribution within the cell

如何表示點雲的機率分布
? multivariate probability function p(~x)l
? mean
? covariance

Scan registration
? The current scan is represented as a point cloud X = {~x1, . . . , ~xn}. Assume
that there is a spatial transformation function T(~p, ~x) that moves a point ~x
in space by the pose ~p.
? Given some PDF p(~x) for scan points , the best pose ~p should be the one
that maximises the likelihood function

Scan registration
? Given a set of points X = {~x1, . . . , ~xn}, a pose ~p, and a transformation
function T(~p, ~x) to transform point ~x in space by ~p, the NDT score
function s(~p) for the current parameter vector is
? Using such a Gaussian approximation, the influence of one point from the
current scan on the NDT score function is

Newton’s algorithm for
? Newton’s algorithm can be used to find the parameters ~p that optimise s(~p)
? Newton’s method iteratively solves the equation H?~p = ?~g
? g and H are partial differential and second order partial differential of
optimizing function. They are

About ND Voxel size
? 太小
? 運算量大，memory 消耗大
? 匹配精確
? 但小於五個點，則很難形成正態分佈
? 太大
? 運算量少
? 匹配不精確

NDT - TKU version
格子重疊
? 提高精確度
? 運算量提高，一點點雲會有八個格子
? Trilinear interpolation

TKU - ND Voxel size
將收斂流程分成兩階段
? Converging state
按照距離切分 ND Voxel size，並運算
? Adjust state
到一定次數後則通通用
最小格子來運算

ENDING
THANKs FOR YOUR ATTENTION.
Reference
1. A 3-D Scan Matching using Improved 3-D Normal Distributions Transform
for Mobile Robotic Mapping(網路上不公開)
2. The Three-Dimensional Normal-Distributions Transform — an Efficient
Representation for Registration, Surface Analysis, and Loop Detection
3. The Normal Distributions Transform:A New Approach to Laser Scan
Matching

Other
1. Parameter
a. voxel size
b. step size
c. iterative times

ROSConJP2018の発表資料です！ http://roscon.jp 講演動画はこちら https://vimeo.com/292065411 組込み向けプロセッサで動作可能な実行性能とメモリ効率を備えるROS1ノードの軽量実行環境mROSを提案する．mROSは、ITRONベースのTOPPERSカーネルと組込み向けTCP/IPスタックのlwIPを核として研究開発しており、ROS仕様に準拠した通信機能を提供する．本研究成果によって、ROS1の豊富なロボット向けコンポーネントの組込みデバイス上への移植が可能となり、その省電力化およびリアルタイム性の向上が期待できる．

翱搁叠-厂尝础惭を动かしてみたTakuya Minagawa

Cvpr 2021 manydepthKenta Tanaka

20190825 vins monoTakuya Minagawa

30th コンピュータビジョン勉強会@関東 DynamicFusionHiroki Mizuno

DynamicFusion is a method for reconstructing and tracking non-rigid scenes in real-time by extending KinectFusion. It uses a volumetric truncated signed distance function (TSDF) to integrate depth maps from multiple viewpoints into a global reconstruction. Live depth frames are aligned to a dense surface prediction generated by raycasting the TSDF. This closes the loop between mapping and localization for tracking dynamic, non-rigid scenes.

ROS の活用による屋外の歩行者空間に適応した自律移動ロボットの開発Yoshitaka HARA

学術研究に役立った場合は、以下の論文を参考文献として引用して頂ければ幸いです。原祥尭: "ROSを用いた自律走行", 日本ロボット学会誌, vol. 35, no. 4, pp. 286--290, 2017. https://www.jstage.jst.go.jp/article/jrsj/35/4/35_35_286/_article/-char/ja 日本ロボット学会第94回ロボット工学セミナー「ロボット用オープンソースソフトウェアとその実用例」講演資料

リクルート式　自然言语処理技术の适応事例绍介Recruit Technologies

厂尝础惭勉强会(笔罢础惭)Masaya Kaneko

笔测迟丑辞苍ではじめるロケーションデータ解析Hiroaki Sengoku

PyDataTokyoでの発表資料をアップしました。 http://pydatatokyo.connpass.com/ スマートフォンやセンサーデバイスの普及に伴い、「ロケーション?インテリジェンス」と言われるように、位置情報データの解析が盛んになってきています。本発表では、地図オタクが位置情報データを扱う上でぶつかる特有の問題やPythonライブラリを活用した対処方法を紹介します。位置情報データにまつわる解析事例も交えつつ、地図の世界に誘います。参考） https://www.youtube.com/watch?v=2sXKpj9Z91k https://www.youtube.com/watch?v=dnPIwmlphII

尝颈顿础搁点群と厂蹿惭点群との位置合わせTakuya Minagawa

mcl_3dl: amcl並に軽量な3-D/6-DoFローカリゼーションパッケージAtsushi Watanabe

ROSConJP2018 (http://roscon.jp/) の発表資料です。 https://github.com/at-wat/mcl_3dl/ 実際の発表中では、bagファイルを再生して、ラップトップ上でローカリゼーションを行うライブデモを行いました。本講演では3-D/6-DoFローカリゼーションパッケージmcl_3dlを紹介する。本パッケージは3-D点群を地図とし、3-D LIDAR、IMU、オドメトリのデータから、パーティクルフィルタで3次元6自由度の位置姿勢を推定する。尤度計算に複数のモデルを用い、モデル毎に適切に点群をサンプリングすること、チャンク化したkd-Treeで地図を格納することで、amclに近い、少ない計算量で動作する。

NDTスキャンマッチング第1回3D勉強会@PFN 2018年5月27日Kitsukawa Yuki

翱搁叠-厂尝础惭の手法解説Masaya Kaneko

06 第5.1節-第5.7節 ROS2に対応したツール／パッケージMori Ken

3次元レジストレーションの基础と翱辫别苍3顿を用いた3次元点群処理Toru Tamaki

【論文紹介】Deep Mimic: Example-Guided Deep Reinforcement Learning of Physics-Based...Tomoyuki Hioki

颁痴分野での最近の脱○○系3选Kazuyuki Miyazawa

Deep Learning Tutorial Ligeng Zhu

This document provides an overview of deep learning including definitions, prerequisites, and examples of techniques like linear regression, multi-layer perceptrons, backpropagation, convolutional neural networks, and frameworks like PyTorch. It defines deep learning as being driven by very deep neural networks, explains why large networks are necessary to handle non-well-defined and ambiguous problems, and discusses how frameworks make deep learning models easy to implement and generalize.

Cvpr 2018 papers review (efficient computing)DonghyunKang12

More Related Content

What's hot (20)

确率的自己位置推定Horiguchi Shuhei

迟蹿,迟蹿2完全理解Koji Terada

Unsupervised Collaborative Learning of Keyframe Detection and Visual Odometry...Masaya Kaneko

尘搁翱厂：组込みデバイス向けの搁翱厂1ノード軽量実行环境Hideki Takase

翱搁叠-厂尝础惭を动かしてみたTakuya Minagawa

Cvpr 2021 manydepthKenta Tanaka

20190825 vins monoTakuya Minagawa

30th コンピュータビジョン勉強会@関東 DynamicFusionHiroki Mizuno

ROS の活用による屋外の歩行者空間に適応した自律移動ロボットの開発Yoshitaka HARA

リクルート式　自然言语処理技术の适応事例绍介Recruit Technologies

厂尝础惭勉强会(笔罢础惭)Masaya Kaneko

笔测迟丑辞苍ではじめるロケーションデータ解析Hiroaki Sengoku

尝颈顿础搁点群と厂蹿惭点群との位置合わせTakuya Minagawa

mcl_3dl: amcl並に軽量な3-D/6-DoFローカリゼーションパッケージAtsushi Watanabe

NDTスキャンマッチング第1回3D勉強会@PFN 2018年5月27日Kitsukawa Yuki

翱搁叠-厂尝础惭の手法解説Masaya Kaneko

06 第5.1節-第5.7節 ROS2に対応したツール／パッケージMori Ken

3次元レジストレーションの基础と翱辫别苍3顿を用いた3次元点群処理Toru Tamaki

【論文紹介】Deep Mimic: Example-Guided Deep Reinforcement Learning of Physics-Based...Tomoyuki Hioki

颁痴分野での最近の脱○○系3选Kazuyuki Miyazawa

确率的自己位置推定Horiguchi Shuhei

迟蹿,迟蹿2完全理解Koji Terada

Unsupervised Collaborative Learning of Keyframe Detection and Visual Odometry...Masaya Kaneko

尘搁翱厂：组込みデバイス向けの搁翱厂1ノード軽量実行环境Hideki Takase

翱搁叠-厂尝础惭を动かしてみたTakuya Minagawa

Cvpr 2021 manydepthKenta Tanaka

20190825 vins monoTakuya Minagawa

30th コンピュータビジョン勉強会@関東 DynamicFusionHiroki Mizuno

ROS の活用による屋外の歩行者空間に適応した自律移動ロボットの開発Yoshitaka HARA

リクルート式　自然言语処理技术の适応事例绍介Recruit Technologies

厂尝础惭勉强会(笔罢础惭)Masaya Kaneko

笔测迟丑辞苍ではじめるロケーションデータ解析Hiroaki Sengoku

尝颈顿础搁点群と厂蹿惭点群との位置合わせTakuya Minagawa

mcl_3dl: amcl並に軽量な3-D/6-DoFローカリゼーションパッケージAtsushi Watanabe

NDTスキャンマッチング第1回3D勉強会@PFN 2018年5月27日Kitsukawa Yuki

翱搁叠-厂尝础惭の手法解説Masaya Kaneko

06 第5.1節-第5.7節 ROS2に対応したツール／パッケージMori Ken

3次元レジストレーションの基础と翱辫别苍3顿を用いた3次元点群処理Toru Tamaki

【論文紹介】Deep Mimic: Example-Guided Deep Reinforcement Learning of Physics-Based...Tomoyuki Hioki

颁痴分野での最近の脱○○系3选Kazuyuki Miyazawa

Similar to NDT-TKU (20)

Deep Learning Tutorial Ligeng Zhu

Cvpr 2018 papers review (efficient computing)DonghyunKang12

Neural machine translation by jointly learning to align and translate.pptxssuser2624f71

The document discusses machine translation techniques including rule-based machine translation (RBMT), statistical machine translation (SMT), and neural machine translation (NMT). It then focuses on neural network approaches, explaining recurrent neural networks (RNNs) and variants like long short-term memory (LSTM) and gated recurrent units (GRU). Finally, it presents a new methodology called RNNsearch that uses an attention mechanism to overcome limitations of fixed-length encodings in encoder-decoder NMT models, showing improved translation performance especially on longer sentences.

DigitRecognition.pptxruvex

The document discusses recognizing handwritten digits using a convolutional neural network model with PyTorch on GPUs. It summarizes the dataset used, which contains images of handwritten digits. The methodology describes building and training a CNN model on GPUs using data parallelism across multiple GPUs. Testing was done varying batch sizes and number of GPUs. Results found that using more GPUs did not always improve performance and larger batch sizes did not necessarily yield better accuracy. Overall, optimal GPU utilization and batch size are important for good model performance when using multiple GPUs.

Superworkflow of Graph Neural Networks with K8S and FugueDatabricks

This document introduces a superworkflow for running Node2Vec on graphs using the Fugue framework on Kubernetes. It describes the Node2Vec algorithm and different steps in the superworkflow, including graph creation and indexing, random walks, Word2Vec preprocessing, and embedding training. The superworkflow provides advantages like parallelizing steps, efficient resource usage through auto-persist and checkpointing. Benchmark results show the superworkflow reduces runtime significantly compared to Spark MLlib, such as reducing a 100M node graph embedding from 6,800 CPU hours to 100 CPU hours and 16 GPU hours. Open source links for the Node2Vec on Fugue project are also provided.

Convolutional and Recurrent Neural NetworksRamesh Ragala

Oxford 05-oct-2012Ted Dunning

This document describes a fast single-pass k-means clustering algorithm. It begins with an overview and rationale for using k-means clustering to enable fast search through large datasets. It then covers the theory behind clusterable data and k-means failure modes. The document outlines ball k-means and surrogate clustering algorithms. It discusses how to implement fast vector search methods like locality sensitive hashing. The document presents results on synthetic datasets and discusses applications like customer segmentation for a company with 100 million customers.

Tomoya Sato Master Thesispflab

This document presents a method for downsampling point cloud data to enable real-time scan matching for autonomous vehicles. It introduces two new downsampling algorithms: Ring Random Filter and Distance Voxel Grid Filter. It evaluates the algorithms based on execution time of scan matching, downsampling time, and relative error compared to raw point cloud data from tests in suburban and city environments. The results show the downsampling enables real-time scan matching with relative errors generally less than 10 cm.

Image Fusion Ehancement using DT-CWT TechniqueIRJET Journal

This document summarizes research on using the dual tree complex wavelet transform (DT-CWT) technique for image fusion. It begins with an abstract describing image fusion algorithms and comparing DT-CWT, discrete wavelet transform (DWT), and a basic fusion algorithm. It then provides background on image fusion, wavelet transforms, the proposed DT-CWT method, and performance metrics like peak signal-to-noise ratio and mean squared error. Simulation results show that DT-CWT yields higher PSNR and lower MSE than DWT and the basic algorithm, indicating better fusion quality.

Direct digital frequency synthesizerVenkat Malai Avichi

This document describes a project on the design and implementation of a Direct Digital Frequency Synthesizer (DDFS) system. The DDFS uses a Numerically Controlled Oscillator (NCO) as its digital part to generate waveforms from a single fixed frequency source. The project aims to understand the working of a DDFS, create a lookup table for the NCO, and modify the table to increase the frequency resolution and reduce errors. The document outlines the existing DDFS systems, proposed improvements, testing methods used and applications of DDFS technology.

Convolutional Neural Network and RNN for OCR problem.Vishal Mishra

This document presents a thesis on using sequence-to-sequence learning with deep learning techniques for optical character recognition. The author aims to convert images of mathematical equations into LaTeX representations. Convolutional neural networks, recurrent neural networks, long short-term memory networks, and attention models are discussed as approaches. Details are provided on the architecture and workings of CNNs, RNNs, and LSTMs. The thesis will propose a model and discuss results and future work.

Parallel kmeans clustering in ErlangChinmay Patel

Matt Purkeypile's Doctoral Dissertation Defense 狠狠撸smpurkeypile

This document summarizes a doctoral dissertation defense presentation on Cove, a practical quantum computer programming framework. The presentation introduces quantum computing concepts, provides a simple example of Shor's factoring algorithm, discusses challenges with programming quantum computers, and outlines Cove's object-oriented approach which aims to address usability issues with existing solutions by programming against interfaces rather than specific implementations. Cove includes a simulated quantum computer for executing code and provides extensibility, documentation, and handles classical computation through the host language (C#).

Data Mining Neural Network for House Price PredictionAnand Kumar

Neighborhood Component Analysis 20071108Ting-Shuo Yo

This document describes Neighbourhood Component Analysis (NCA), a machine learning algorithm that learns an optimal distance metric from training data to improve k-nearest neighbors (KNN) classification. NCA formulates the KNN classification error on training data as an objective function and learns a linear transformation of the data to minimize this error by optimizing the objective function. It then performs KNN classification on test data using the learned distance metric. The document presents the NCA algorithm, evaluates it on several datasets, and discusses its performance compared to other classification methods.

prescalers and dual modulus prescalersSakshi Bhargava

This document presents a unified approach to analyzing prescalers and dual modulus prescalers for low-power systems. It introduces various flip-flop circuit techniques like true single phase clock, extended true single phase clock, and hybrid master slave flip-flop that can be used to build prescalers. Prescalers are frequency dividers that can divide an input frequency by an integer value. Dual modulus prescalers can divide by two integers like N and N+1. The document discusses the construction of divide-by-N prescalers and divide-by-N/N+1 dual modulus prescalers. It then shows simulation results of various prescalers and compares the performance of the proposed divide

ACM 2013-02-25Ted Dunning

This document proposes a fast single-pass k-means clustering algorithm. It begins by discussing the rationale and theory behind k-means clustering, focusing on using it to enable fast search through large datasets. It then describes the ball k-means and surrogate methods algorithms, explaining how they provide provably better clustering for highly clusterable data. Implementation details are covered regarding search techniques, vector representations, and parallelization. Evaluation results show the approach works well on synthetic and real-world datasets, providing an order of magnitude speed improvement over traditional k-means while maintaining clustering quality. The document concludes by discussing applications for nearest neighbor search through large customer datasets.

PR-284: End-to-End Object Detection with Transformers(DETR)Jinwon Lee

TensorFlow Korea ?????? PR12 284?? ?? review???. ?? ??? Facebook?? ?? DETR(DEtection with TRansformer) ???. arxiv-sanity? top recent/last year?? ?? ??? ???? ?? ????? ???(http://www.arxiv-sanity.com/top?timefilter=year&vfilter=all) ??? ICLR 2021? submit? ViT? ??? ?? Transformer? CNN? ???? ? ??? ?? ???? ?? ??? ????, ? ? ECCV? ??? ???? feature extraction ??? CNN? ???? ??? transformer? ???? ????? Object Detection? ???? ??? ??? ??? ????? ?????. ? ????? detection ???? anchor box? NMS(Non Maximum Supression)? ?? heuristic ?? ?? ???? ???? ?? ????, ?? ??? ?? object detection ??? ???? ??? end-to-end ???? ???? ??? ??? ???? ????. ? ????? bounding box? ???? ??? set prediction problem(??? ???? ??, ??? ???)?? ?? transformer? ??? end-to-end ??? ????? ???????. anchor box? ???? NMS? ???? DETR ????? ??? ??? ?????? ??? ??????! ????: https://youtu.be/lXpBcW_I54U ????: https://arxiv.org/abs/2005.12872

[20240422_LabSeminar_Huy]Taming_Effect.pptxthanhdowork

MetaPerturb: Transferable Regularizer for Heterogeneous Tasks and ArchitecturesMLAI2

MetaPerturb is a meta-learned perturbation function that can enhance generalization of neural networks on different tasks and architectures. It proposes a novel meta-learning framework involving jointly training a main model and perturbation module on multiple source tasks to learn a transferable perturbation function. This meta-learned perturbation function can then be transferred to improve performance of a target model on an unseen target task or architecture, outperforming baselines on various datasets and architectures.

Deep Learning Tutorial Ligeng Zhu

Cvpr 2018 papers review (efficient computing)DonghyunKang12

Neural machine translation by jointly learning to align and translate.pptxssuser2624f71

DigitRecognition.pptxruvex

Superworkflow of Graph Neural Networks with K8S and FugueDatabricks

Convolutional and Recurrent Neural NetworksRamesh Ragala

Oxford 05-oct-2012Ted Dunning

Tomoya Sato Master Thesispflab

Image Fusion Ehancement using DT-CWT TechniqueIRJET Journal

Direct digital frequency synthesizerVenkat Malai Avichi

Convolutional Neural Network and RNN for OCR problem.Vishal Mishra

Parallel kmeans clustering in ErlangChinmay Patel

Matt Purkeypile's Doctoral Dissertation Defense 狠狠撸smpurkeypile

Data Mining Neural Network for House Price PredictionAnand Kumar

Neighborhood Component Analysis 20071108Ting-Shuo Yo

prescalers and dual modulus prescalersSakshi Bhargava

ACM 2013-02-25Ted Dunning

PR-284: End-to-End Object Detection with Transformers(DETR)Jinwon Lee

[20240422_LabSeminar_Huy]Taming_Effect.pptxthanhdowork

MetaPerturb: Transferable Regularizer for Heterogeneous Tasks and ArchitecturesMLAI2

Recently uploaded (20)

Threat Modeling a Batch Job System - AWS Security Community DayTeri Radichel

I've been working on building a batch job framework for a few years now and blogging about it in the process. This presentation explains how and why I started building and writing about this system and the reason it changed from deploying one simple batch job to a much bigger project. I explore a number of recent data breaches, how they occurred, and what may have prevented them along the way. We consider how what make goes into an effective security architecture and well-designed security controls that avoid common pitfalls. There are friend links to many blog posts in the notes of the presentation that bypass the paywall. Topics include security architecture, IAM, encryption (KMS), networking, MFA, source control, separation of duties, supply chain attacks, and more.

Future?Proofing the Nordic Economy with GenAIPete Nieminen

Ricardo Jebb Bruno - A Structural CAD TechnicianRicardo Jebb Bruno

Ricardo Jebb Bruno is a skilled Structural CAD Technician with over 10 years of experience. He specializes in structural analysis, design, and project management, and is proficient in AutoCAD, Revit, and SolidWorks. A graduate of the University of Miami with a degree in Civil Engineering, he currently works at Metrix Structural Group. Ricardo is a member of the American Society of Civil Engineers and the National CAD Society, and volunteers with Habitat for Humanity. His hobbies include 3D printing and sci-fi media.

BrightonSEO April 2025 - hreflang XML E-Commerce - Nick Samuel.pdfNick Samuel

Brighton April 2025 was my first ever attempt at public presentation. Full title was "XML + hreflang: A Practical Guide for Large E-Commerce Sites The presentation was suitable for anyone involved in deploying or managing hreflang for ecommerce websites (big and small). This talk challenges the sometimes-held assumption that HTML hreflang is automatically the “better” option compared to XML hreflang Sitemaps by exploring the advantages and disadvantages of each method. Drawing upon 12 years of experience in International SEO, I shared common scenarios where XML hreflang Sitemaps could be more effective compared to HTML, as well as practical tips for prioritising and troubleshooting your hreflang deployment. By reading this deck you will be aware of the possibilities of XML hreflang Sitemaps, and an understanding of when they might be suitable to use for your own website.

From SBOMs to xBOMs to Transparency - Pavel Shukhman at OWASP Ottawa on 2025-...Pavel Shukhman

Introduction to Generative AI refers to a subset of artificial intelligenceKongu Engineering College, Perundurai, Erode

Data Modelling For Software Engineers (Devoxx GR 2025).pdfScott Sosna

Really, data modeling? Is that even a thing any more? The days of formal data modeling are definitely years in the rearview mirror, empowered teams define their data as they see fit, implement, and move on. Done. And we'll deal with short-comings down the road when they arise, that's Agile, let's keep moving forward (to data architects' frustration when trying to make sense of it all after the fact). But "modeling data" extends beyond what is persisted in a database server: API Payloads, messages, configuration files, document metadata, Redis indexes are forms of data we define and work with regularly. If I've got your attention, join me to discuss data modeling, this time from a software engineering perspective!

Cybersecurity-Threat-Landscape-March-31-April-7-2025.pdfJoe Shenouda

Introduction to PHP from Beginning to Endchristopherneo4

April Patch TuesdayIvanti

Ivanti’s Patch Tuesday breakdown goes beyond patching your applications and brings you the intelligence and guidance needed to prioritize where to focus your attention first. Catch early analysis on our Ivanti blog, then join industry expert Chris Goettl for the Patch Tuesday Webinar Event. There we’ll do a deep dive into each of the bulletins and give guidance on the risks associated with the newly-identified vulnerabilities.

TrustArc Webinar - Data Privacy and Cyber Security: A Symbiotic RelationshipTrustArc

In today’s digital age, data has become an organization’s lifeblood. As the use of digital technologies continues to escalate, so do the risks associated with personal data, which continue to grow exponentially as well. To effectively safeguard personal and sensitive information, organizations must understand the intricate relationship between data privacy, cybersecurity, and incident response. Data privacy and cybersecurity are two sides of the same coin. Data privacy focuses on how personal data is to be collected, used, stored, shared and controlled, while cybersecurity aims to protect systems and networks from unauthorized access, digital attacks, malware and data breaches. However, even with the best data privacy and security measures in place, cyber incidents can still occur. A well-prepared incident response plan is crucial for minimizing the impact of a breach and restoring normal operations. Join our experts on this webinar to discuss how data privacy, cybersecurity, and incident response interact and are essential for safeguarding your organization’s digital assets. This webinar will review: - How data privacy and cybersecurity intersect - How to develop a comprehensive privacy and security strategy to safeguard personal and sensitive information - What are suggestions and expectations around incident response

Fran?ais Patch Tuesday - AvrilIvanti

Top 10 Mobile Hacking Tools – 2025 Editionanishachhikara2122

Explore the most powerful and widely-used mobile hacking tools in cybersecurity today. This presentation covers top tools like MobSF, Frida, Hopper, Ghidra, Objection, and more—highlighting their core features, use cases, platforms, and practical tips. Whether you're a security researcher, ethical hacker, or mobile app developer, this slide deck offers a well-rounded introduction to both static and dynamic analysis tools for Android and iOS. Ideal for training, awareness, and professional development.

Meet, Greet, and Explore Agentic AI with UiPath ScotlandUiPathCommunity

After a long break, we're excited to reconnect and reignite our community. Join us for this engaging 'Meet & Greet' event, where you'll have the opportunity to connect with fellow RPA enthusiasts, industry professionals, and AI innovators. In this introductory session, we'll delve into the fascinating world of agentic AI, exploring how AI-powered agents are revolutionizing automation by bringing intelligence, autonomy, and decision-making capabilities to RPA workflows. ? What to expect: Networking opportunities with the UiPath Community in Scotland A clear and engaging introduction to agentic AI Interactive Q&A session to clarify your questions and ideas Whether you're an experienced developer, a business leader, or completely new to automation, come along to learn, share, and connect. Let's innovate together with UiPath Community Scotland! Speaker/Chapter Leader: ???Gunashekhar Kotla, UiPath MVP, AI Automation Consultant @EY This session streamed live on April 10, 2025, 14:00 GMT. Check out all our upcoming UiPath Community sessions at: ? https://community.uipath.com/events/#... Join UiPath Community Scotland chapter: ? https://community.uipath.com/scotland...

MariaDB Berlin Roadshow 狠狠撸s - 8 April 2025MariaDB plc

CitrineOS: Bridging the Past and Future of EV Charging with OCPP 1.6 & 2.x Su...DanBrown980551

Join us for an exclusive webinar showcasing the latest advancements in CitrineOS, the open-source, API-first Charge Station Management System. With expanded support for OCPP 1.6 alongside full OCPP 2.x compatibility, CitrineOS is now more adaptable than ever—allowing operators to seamlessly manage both legacy and next-generation EV chargers. Discover how our new dynamic UI enhances operational efficiency, providing native EV charging network management with intuitive TimeSeries data views for authorizations, transactions, charging stations, and locations. Learn about technical upgrades, including the addition of GraphQL, improved file storage flexibility, and a refactored core designed to support multiple OCPP protocols. Don’t miss this opportunity to see how CitrineOS is redefining charge station management with a future-proof platform that evolves with the industry. Register now to stay ahead in the rapidly changing EV charging landscape!

CEE Software Development M&A Report 2025Yevgen Sysoyev

Q1 FY26 TUG Leader Quarterly Call - APAC / EMEAlward7

AC1-intro-agenda-Agile concepts in an enterprise environmentDennis Van Aelst

AI in Bioinformatics: How Artificial Intelligence is Revolutionizing Healthca...Vadim Nareyko

Threat Modeling a Batch Job System - AWS Security Community DayTeri Radichel

Future?Proofing the Nordic Economy with GenAIPete Nieminen

Ricardo Jebb Bruno - A Structural CAD TechnicianRicardo Jebb Bruno

BrightonSEO April 2025 - hreflang XML E-Commerce - Nick Samuel.pdfNick Samuel

From SBOMs to xBOMs to Transparency - Pavel Shukhman at OWASP Ottawa on 2025-...Pavel Shukhman

Introduction to Generative AI refers to a subset of artificial intelligenceKongu Engineering College, Perundurai, Erode

Data Modelling For Software Engineers (Devoxx GR 2025).pdfScott Sosna

Cybersecurity-Threat-Landscape-March-31-April-7-2025.pdfJoe Shenouda

Introduction to PHP from Beginning to Endchristopherneo4

April Patch TuesdayIvanti

TrustArc Webinar - Data Privacy and Cyber Security: A Symbiotic RelationshipTrustArc

Fran?ais Patch Tuesday - AvrilIvanti

Top 10 Mobile Hacking Tools – 2025 Editionanishachhikara2122

Meet, Greet, and Explore Agentic AI with UiPath ScotlandUiPathCommunity

MariaDB Berlin Roadshow 狠狠撸s - 8 April 2025MariaDB plc

CitrineOS: Bridging the Past and Future of EV Charging with OCPP 1.6 & 2.x Su...DanBrown980551

CEE Software Development M&A Report 2025Yevgen Sysoyev

Q1 FY26 TUG Leader Quarterly Call - APAC / EMEAlward7

AC1-intro-agenda-Agile concepts in an enterprise environmentDennis Van Aelst

AI in Bioinformatics: How Artificial Intelligence is Revolutionizing Healthca...Vadim Nareyko

NDT-TKU

1. NDT - TKU heaton

2. What is ndt_tku ?A 3-D Scan Matching using Improved 3-D Normal Distributions Transform for Mobile Robotic Mapping ?名古屋大學竹內先生(TAKEUCHI)提出的 NDT 優化版 ?Autoware/ros/src/computing/perception/localization/packages/n dt_localizer/nodes/ndt_matching_tku/

3. Why is ndt_tku ?是指導教授提出的 ?PCL 的 cuda 化極度麻煩，工程師表示不如自幹一套，然後 cuda 化

4. Outline ndt_tku ? ND ? NDT in slam ? NDT_TKU

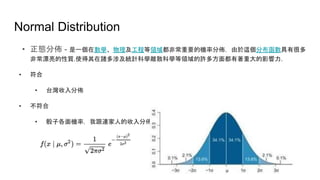
5. Normal Distribution ? 正態分佈 - 是一個在數學、物理及工程等領域都非常重要的機率分佈，由於這個分布函數具有很多非常漂亮的性質.使得其在諸多涉及統計科學離散科學等領域的許多方面都有著重大的影響力. ? 符合 ? 台灣收入分佈 ? 不符合 ? 骰子各面機率，我跟連家人的收入分佈。

6. Normal Distribution Transform Subdivide the space occupied by the scan into a grid of cells. A PDF is computed for each cell, based on the point distribution within the cell

7. NDT in tunnel - 3D

8. 如何表示點雲的機率分布 ? multivariate probability function p(~x)l ? mean ? covariance

9. Scan registration ? The current scan is represented as a point cloud X = {~x1, . . . , ~xn}. Assume that there is a spatial transformation function T(~p, ~x) that moves a point ~x in space by the pose ~p. ? Given some PDF p(~x) for scan points , the best pose ~p should be the one that maximises the likelihood function

10. Scan registration ? Given a set of points X = {~x1, . . . , ~xn}, a pose ~p, and a transformation function T(~p, ~x) to transform point ~x in space by ~p, the NDT score function s(~p) for the current parameter vector is ? Using such a Gaussian approximation, the influence of one point from the current scan on the NDT score function is

11. Newton’s algorithm for ? Newton’s algorithm can be used to find the parameters ~p that optimise s(~p) ? Newton’s method iteratively solves the equation H?~p = ?~g ? g and H are partial differential and second order partial differential of optimizing function. They are

12. 流程

13. 我知道大家看數字很痛苦但我只是要說算這個很麻煩。

14. About ND Voxel size ? 太小 ? 運算量大，memory 消耗大 ? 匹配精確 ? 但小於五個點，則很難形成正態分佈 ? 太大 ? 運算量少 ? 匹配不精確

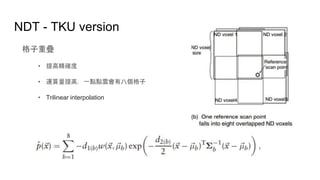
15. NDT - TKU version 格子重疊 ? 提高精確度 ? 運算量提高，一點點雲會有八個格子 ? Trilinear interpolation

16. 图片有感

17. TKU - ND Voxel size 將收斂流程分成兩階段 ? Converging state 按照距離切分 ND Voxel size，並運算 ? Adjust state 到一定次數後則通通用最小格子來運算

18. ENDING THANKs FOR YOUR ATTENTION. Reference 1. A 3-D Scan Matching using Improved 3-D Normal Distributions Transform for Mobile Robotic Mapping(網路上不公開) 2. The Three-Dimensional Normal-Distributions Transform — an Efficient Representation for Registration, Surface Analysis, and Loop Detection 3. The Normal Distributions Transform:A New Approach to Laser Scan Matching

19. Other 1. Parameter a. voxel size b. step size c. iterative times

20. score detail

Editor's Notes

#4: 虽然是这样说，但是这是好几周前说的
#6: 连续的，数学只要能表示出来就能算
#7: 先切成一格一格 The normal-distributions transform can be described as a method for compactly representing a surface. 正態分佈給出了點雲的分段平滑表示，具有連續的導數。每個PDF可以看作是局部表面的近似值，描述了表面的位置以及其取向和平滑度。 A 2D laser scan from a mine tunnel (shown as points) and the PDFs describing the surface shape. Each cell is a square with 2 m side length in this case. Brighter areas represent a higher probability. PDFs have been computed only for cells with more than five points.
#8: 3D-NDT surface representation for a tunnel section, seen from above. Brighter, denser parts represent Higher probabilities. The cells have a side length of 1 m
#9: D-dimensional normal random process, the likelihood of having measured ~x is where ~yk=1,..., m are the positions of the reference scan points contained in the cell. 正態分佈給出了點雲的分段平滑表示，具有連續的導數。每個PDF可以看作是局部表面的近似值，描述了表面的位置以及其取向和平滑度。协方差矩阵的特征向量和特征值可以表达表面信息 . Each PDF can be seen as an approximation of the local surface, describing the position of the surface as well as its orientation and smoothness
#10: 當前掃描被表示為點雲X = {?x1，...。。。，?xn}。假設有一個空間變換函數T（?p，?x）通過姿態p移動空間中的點?x。給定一些用於掃描點的PDF p（?x）（例如，等式6.1），最佳姿態p應該是最大化似然函數的姿態使用近似法去取得最近值, 這是一個疊代過程 n學生身高(X) à X~(135, 102)
#11: 收斂的參數計算學力偏差值，上一頁的 -4 , -2 , 0 , 2 , 4 ，為只表示的點值正規化
#12: 老樣子超過15個符號我們就不要理會 https://www.youtube.com/watch?v=Quw4ZHLH2CY 利用微分找出切線，疊代法趨近找出 function = 0 的根
#13: s
#14: 但跟其他算法比算快了(Iterative Closest Point，迭代最近点)
#15: 格子大小 ND Voxel size 包含點多少的定值，通常至大於五個點，形成正態分布太大也會讓nd不好形成迭代次數 iterative times 決定格子大小變成最主要優化的手段必須取決sensor 類型
#16: 這並非TKU提出來的。 Peter Biber and Wolfgang Stra?er: “The Normal Distributions Transform:A New Approach to Laser Scan Matching”, Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2743–2748, 2003 那麼就會需要降低運算量
#18: 通常是四次切割
#19: CODE TRANSFER TO JJ

狠狠撸

NDT-TKU

Recommended

More Related Content

What's hot (20)

Similar to NDT-TKU (20)

Recently uploaded (20)

NDT-TKU

Editor's Notes