SGD+α: 確率的勾配降下法の現在と未来
84 likes44,628 views
SGDの最新の拡張手法を紹介： Importance-aware UpdateやNormalized Online Learningなど．SGD+αはここまで出来る！
![Importance-aware step width
ステップ幅の再設定式
Table 1: Importance Weight Aware Updates for Various Loss Functions
Loss
`(p, y)
Update s(h)
?
?
>
p y
Squared
(y p)2
1 e h?x x
x> x
Logistic
log(1 + e
Exponential
e
y log
Logarithmic
Hellinger
Hinge
? -Quantile
p
( p
y
p
p
2
y)
yp
)
yp
+ (1
p
( 1
y) log
p
1 y
1 p
p
1
max(0, 1 yp)
if y > p
? (y p)
if y ? p (1 ? )(p y)
(6) gives a di?erential equation whose solution is the
result of a continuous gradient descent process.
As a sanity check we rederive (5) using (6). For
@`
squared loss @p = p y and we get a linear ODE:
y)2
> x+yp+eyp
) h?x> x eyp
for y 2 { 1, 1}
yx> x
py log(h?x> x+epy )
for y 2 { 1, 1}
x> xy
p
p 1+ (p 1)2 +2h?x> x
if y = 0
p x> x
p
p2 +2h?x> x
if y = 1
x> x
>
1
p 1+ 4 (12h?x x+8(1 p)3/2 )2/3
if y = 0
x> x
1
p 4 (12h?x> x+8p3/2 )2/3
if y = 1
x> x
1 yp
y min h?, x> x for y 2 { 1, 1}
if y > p
? min(h?, ?yx>p )
x
p y
if y ? p (1 ? ) min(h?, (1 ? )x> x )
W (eh?x
solution to (6) has no simple form for all y 2 [0, 1] but
for y 2 {0, 1} we get the expressions in table 1.
3.1.1
(Karampatziakis+ 11) より
Hinge Loss and Quantile Loss
Two other commonly used loss function are the hinge
loss
21 and the ? -quantile loss where ? 2 [0, 1] is a parameter function. These are di?erentiable everywhere](https://image.slidesharecdn.com/sgdfuturebest-131017193043-phpapp02/85/SGD-21-320.jpg)
![線形収束するSGD
?
?線形予測器ならば，一データにつきスカラー
f が強凸かつ各 fn (·) が滑らかな時，線形収束
(?oat/double)を一つ持てば良い
?正則化項を加えたい場合
?SAGでは，L1を使ったスパース化の収束性は
未証明 (近接勾配法)
?SDCA [Shalev+ 13], MISO[Mairal 13]
39](https://image.slidesharecdn.com/sgdfuturebest-131017193043-phpapp02/85/SGD-39-320.jpg)
SGD+α: 確率的勾配降下法の現在と未来
- 1. 2013/10/17 PFIセミナー SGD+α 確率的勾配降下法の現在と未来 東京大学 情報理工学系研究科 大岩 秀和 / @kisa12012
- 2. 自己紹介 ?大岩 秀和 (a.k.a. @kisa12012) ?所属: 東大 数理情報 D2 (中川研) ?研究: 機械学習?言語処理 ?オンライン学習/確率的最適化/スパース正 則化 etc... ?前回のセミナー: 能動学習入門 ?PFI: インターン(10) -> アルバイト(-12) 2
- 3. 今日の話 1/2 ?みんな大好き（？）確率的勾配降下法 ?Stochastic Gradient Descent (SGD) ?オンライン学習の文脈では，Online Gradient Decent (OGD)と呼ばれる ?SGDは便利だけど，使いにくい所も ?ステップ幅の設定方法とか 3
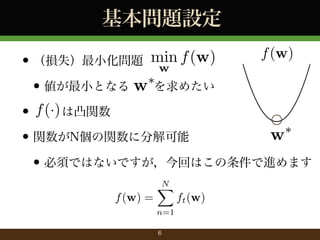
- 6. 基本問題設定 min f (w) f (w) ? （損失）最小化問題 w ? ? 値が最小となる w を求めたい f (·) は凸関数 ? ? w 関数がN個の関数に分解可能 ? ? 必須ではないですが，今回はこの条件で進めます f (w) = N X n=1 6 ft (w)
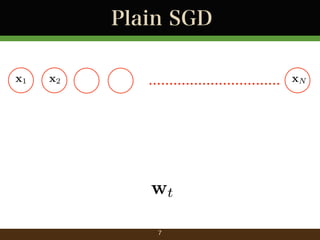
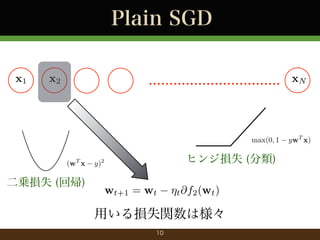
- 9. Plain SGD x1 x2 ................................ xN wt+1 = wt ?t @f2 (wt ) 選んだデータに対応する勾配でパラメータ更新 9
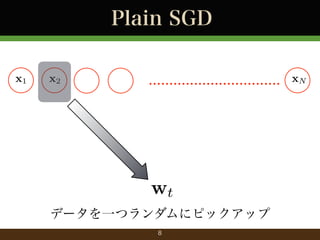
- 10. Plain SGD x1 x2 ................................ xN max(0, 1 (wT x 二乗損失 (回帰) ヒンジ損失 (分類) y)2 wt+1 = wt ?t @f2 (wt ) 用いる損失関数は様々 10 ywT x)
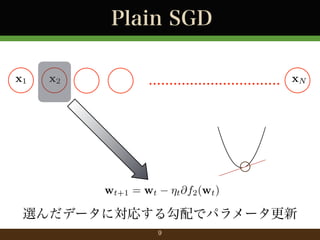
- 11. Plain SGD ?関数を一つだけサンプルして，勾配を計算 wt+1 = wt ?t rfnt (wt ) ? 関数 fnt (·) の値が一番小さくなる 方向へパラメータを更新 ?t でステップの幅を調整 ? ?微分不可能な場合も劣勾配で 11
- 12. Pros and Cons of Plain SGD wt+1 = wt ?t rfnt (wt ) ?長所 ?大規模データに有効 (Bottou+ 11) ? そこそこの 解がすぐに欲しい時 ?実装?デバッグ?実験サイクルを回すのが楽 ?ノウハウ集 (Bottou 12) ?最適解への収束証明あり 12
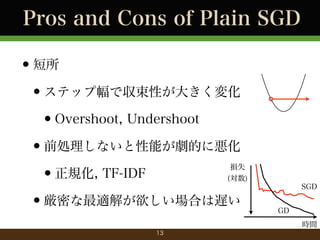
- 13. Pros and Cons of Plain SGD ?短所 ?ステップ幅で収束性が大きく変化 ?Overshoot, Undershoot ?前処理しないと性能が劇的に悪化 ?正規化, TF-IDF ?厳密な最適解が欲しい場合は遅い 損失 (対数) SGD GD 時間 13
- 15. 今日紹介する+α ? Importance-aware Update ? ステップ幅の問題を緩和 ? Normalized Online Learning ? 前処理なし，オンラインで特徴量の正規化 ? Linear Convergence SGD ? バッチデータに対して，線形収束するSGD ? 他にもAdaGrad／省メモリ化等を紹介したかったで (Karampatziakis+ 11) (Stéphane+ 13) (Le Roux+ 12) すが，略 15
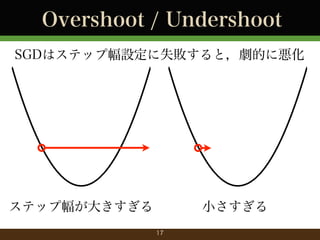
- 18. ステップ幅設定は大変 w = (inf, inf, . . . ) ?Overshootで生じるnan/infの嵐 ?Cross-Validationで最適ステップ幅探しの旅 ?つらい ?ステップ幅選択に悩みたくない ?Importance-aware Update ?キーワード: Invariance, Safety 18
- 20. Importance-aware Update (Karampatziakis+ 11) ?Invarianceを満たすステップ幅の再設定法 ?線形予測器では変化するのはステップ幅のみ ?主な損失関数のステップ幅は，閉じた式で計 算可能 ?L2正則化等が入っても大丈夫 ?Regret Boundの証明あり 20
- 21. Importance-aware step width ステップ幅の再設定式 Table 1: Importance Weight Aware Updates for Various Loss Functions Loss `(p, y) Update s(h) ? ? > p y Squared (y p)2 1 e h?x x x> x Logistic log(1 + e Exponential e y log Logarithmic Hellinger Hinge ? -Quantile p ( p y p p 2 y) yp ) yp + (1 p ( 1 y) log p 1 y 1 p p 1 max(0, 1 yp) if y > p ? (y p) if y ? p (1 ? )(p y) (6) gives a di?erential equation whose solution is the result of a continuous gradient descent process. As a sanity check we rederive (5) using (6). For @` squared loss @p = p y and we get a linear ODE: y)2 > x+yp+eyp ) h?x> x eyp for y 2 { 1, 1} yx> x py log(h?x> x+epy ) for y 2 { 1, 1} x> xy p p 1+ (p 1)2 +2h?x> x if y = 0 p x> x p p2 +2h?x> x if y = 1 x> x > 1 p 1+ 4 (12h?x x+8(1 p)3/2 )2/3 if y = 0 x> x 1 p 4 (12h?x> x+8p3/2 )2/3 if y = 1 x> x 1 yp y min h?, x> x for y 2 { 1, 1} if y > p ? min(h?, ?yx>p ) x p y if y ? p (1 ? ) min(h?, (1 ? )x> x ) W (eh?x solution to (6) has no simple form for all y 2 [0, 1] but for y 2 {0, 1} we get the expressions in table 1. 3.1.1 (Karampatziakis+ 11) より Hinge Loss and Quantile Loss Two other commonly used loss function are the hinge loss 21 and the ? -quantile loss where ? 2 [0, 1] is a parameter function. These are di?erentiable everywhere
- 22. Safety ?Importance-aware Updateとなった二乗損失や ヒンジ損失は，Safetyの性質を持つ Safety T wt+1 x y T wt x y 0 が必ず満たされる 領域を超えない 22
- 23. No more step width war! ?SafetyによりOvershootの危険性が減る ?初期ステップ幅を大きめにとれる ?ステップ幅の精密化により，精度も改善 ?賢いステップ幅選択方法は他にも提案 ?(Duchi+ 10), (Schaul+ 13)... 23
- 24. 3. Normalized Online Learning 24
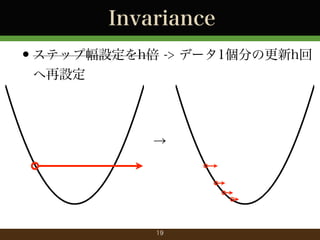
- 25. 特徴量の正規化 ? 各特徴量のスケールに強い影響を受ける ? スケールの上限／下限の差が大きいほど，理論的にも実 証的にも性能悪化 ? バッチ学習の場合は前処理で正規化する場合がほとんど ? オンライン学習では，前処理が不可能な場合がある ? 全部のデータを前もって用意出来ない etc. x = (1.0, 5.2, . . . ) x = (1000.0, 5.2, . . . ) 25 x = (0.001, 5.2, . . . )
- 26. Normalized Online Learning (Stéphane+ 13) s1 s2 ................................ wt = (1.0, 2.0, . . . , 5.0) 各特徴量に，最大値保存用のボックスを設置 26 sD
- 27. Normalized Online Learning s1 s2 ................................ x2 = (2.0, 1.0, . . . , 5.0) wt = (1.0, 2.0, . . . , 5.0) データを一つランダムにピックアップ 27 sD
- 28. Normalized Online Learning s1 s2 ................................ x2 = (2.0, 1.0, . . . , 5.0) wt = (1.0, 2.0, . . . , 5.0) 選択したデータの各特徴量の値が 最大値を超えていないかチェック 28 sD
- 29. Normalized Online Learning 2.0 s2 ................................ sD If 2.0 > s1 x2 = (2.0, 1.0, . . . , 5.0) 1.0 ? s2 1 wt = ( 2 , 2.0, . . . , 5.0) 2.0 もし超えていたら，正規化せずに過去データを 処理してしまった分，重みを補正 29
- 30. Normalized Online Learning 2.0 ................................ s2 wt+1 = wt sD ?t g (@f2 (wt ), s1:D ) x2 = (2.0, 1.0, . . . , 5.0) あとは，サンプルしてきたデータを使って， 正規化しながら確率的勾配法でアップデート 30
- 31. Normalized Online Learning ? オンライン処理しながら自動で正規化 ? スケールを（あまり）気にせず，SGDを回せるように！ ? スケールも敵対的に設定されるRegret Boundの証明付き Algorithm 1 NG(learning rate ?t ) Algorithm 2 NAG(learning rate ?) 1. Initially wi = 0, si = 0, N = 0 1. Initially wi = 0, si = 0, Gi = 0, N 2. For each timestep t observe example (x, y) 2. For each timestep t observe example (a) For each i, if |xi | > si (a) For each i, if |xi | > si wi si i. wi |xi | ii. si |xi | P (b) y = i wi xi ? P x2 i (c) N N + i s2 wi s2 i |xi |2 i. wi ii. si |xi | P (b) y = i wi xi ? P (c) N N+ i (d) For each i, i. wi wi x2 i 2 si (d) For each i, y ,y) t ?t N s1 @L(?i 2 @w i 31 i. Gi Gi + ii. wi wi i ? @L(?,y) y @wi (Stéphane+ 13)より q t ? N si ?2 1 p @L Gi @
- 32. 4. Linear Convergence SGD 32
- 33. 線形収束するSGD ?Plain SGDの収束速度 p 一般的な条件の下で凸関数 O(1/ T ) ? O(1/T ) 滑らかで強凸 ? ?使用データが予め固定されている場合 SGD+αで線形収束が可能に O(c ) ? ?厳密な最適解を得たい場合もSGD+α ? f (w) f (w? ) T 33
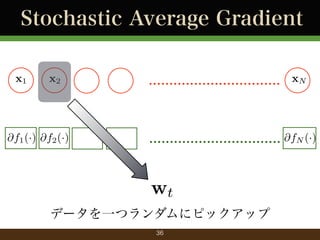
- 34. Stochastic Average Gradient (Le Roux+ 12) x1 x2 ................................ xN wt 34
- 35. Stochastic Average Gradient x1 x2 @f1 (·) @f2 (·) ................................ xN ................................ @fN (·) wt 各データに，勾配保存用のボックスを一つ用意 35
- 36. Stochastic Average Gradient x1 x2 @f1 (·) @f2 (·) ................................ xN ................................ @fN (·) wt データを一つランダムにピックアップ 36
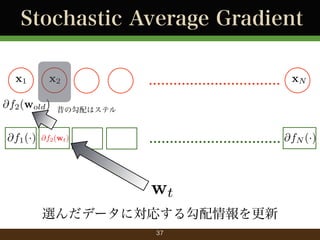
- 37. Stochastic Average Gradient x1 x2 @f2 (wold ) @f1 (·) ................................ xN 昔の勾配はステル @f2 (wt ) ................................ @fN (·) wt 選んだデータに対応する勾配情報を更新 37
- 38. Stochastic Average Gradient x1 x2 ................................ xN 新しい勾配もあれば @f1 (·) 古い勾配もある ................................ @fN (·) @f2 (wt ) wt+1 = wt N X ?t @fn (·) N n=1 全勾配情報を使って，重みベクトルを更新 38
- 39. 線形収束するSGD ? ?線形予測器ならば，一データにつきスカラー f が強凸かつ各 fn (·) が滑らかな時，線形収束 (?oat/double)を一つ持てば良い ?正則化項を加えたい場合 ?SAGでは，L1を使ったスパース化の収束性は 未証明 (近接勾配法) ?SDCA [Shalev+ 13], MISO[Mairal 13] 39
- 40. まとめ ? SGD+α ? ステップ幅設定／自動正規化／線形収束化 ? その他，特徴適応型のステップ幅調整／省メモリ化 等，SGD拡張はまだまだ終わらない ? フルスタックなSGDピザが出来る．．？ ? 近いうちに，ソルバーの裏側でよしなに動いてくれ る．．はず？ ? そんなソルバーを募集中 40
- 41. 参考文献 ? L. Bottou, O.Bousquet, The Tradeo?s of Large-Scale Learning , Optimization for Machine Learning, 2011. ? ? L. Bottou, Stochastic Gradient Descent Tricks , Neural Networks, 2012. Nikos Karampatziakis, John Langford, "Online Importance Weight Aware Updates", UAI, 2011. ? John C. Duchi, Elad Hazan, Yoram Singer, "Adaptive Subgradient Methods for Online Learning and Stochastic Optimization", JMLR, 2011. ? Tom Schaul, Sixin Zhang and Yann LeCun., "No more Pesky Learning Rates", ICML, 2013. ? ? Stéphane Ross, Paul Mineiro, John Langford, "Normalized Online Learning", UAI, 2013. Nicolas Le Roux, Mark Schmidt, Francis Bach, Stochastic Gradient Method with an Exponential Convergence Rate for Finite Training Sets , NIPS, 2012. ? Shai Shalev-Shwartz, Tong Zhang, Stochastic Dual Coordinate Ascent Methods for Regularized Loss Minimization , JMLR, 2013. ? Julien Mairal, Optimization with First-Order Surrogate Functions , ICML, 2013. 41