�ݺ�ߣ

z
Is this
normal?
Why do you
think its not
normal?

z
Is this normal?
Why should we
normalize this
kind of
practice?

z
Is this normal?
Why should we
NOT normalize
this kind of
behavior?

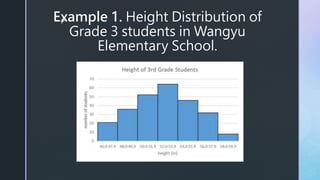
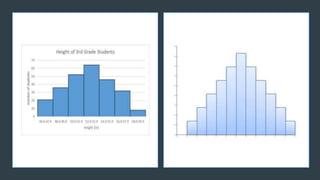
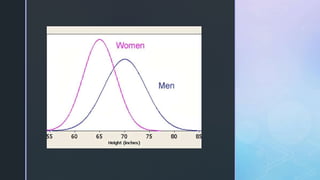
z
Example 1. Height Distribution of
Grade 3 students in Wangyu
Elementary School.

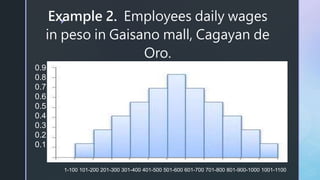
z
Example 2. Employees daily wages
in peso in Gaisano mall, Cagayan de
Oro.
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
1-100 101-200 201-300 301-400 401-500 501-600 601-700 701-800 801-900-1000 1001-1100

z
Normal Distribution is
also called as
Gaussian Distribution.
It is the probability of
continuous random
variable and consider
as the most
important curve in
statistics.

z
z
The equation
of the
theoretical
normal
distribution
is given by
the formula.

Properties of Normal
Curve.
1.The distribution curve is bell
shaped.
2.The curve is symmetrical to
its center, the mean.
3.The mean, median and
mode coincide at the center.

Properties of Normal
Curve.
3. The width of the curve is determined
by the standard deviation of the
distribution.
4. The curve is asymptotic to the
horizontal axis.
5. The area under the curve is 1, thus
it represents the probability or
proportion, or percentage associated
with specific sets of measurements
values.

Normal distribution is determined by two
parameters: the mean and the standard
deviation.
1. Mean Value
2. Standard Deviation Value

z
z
Empirical Rule referred to as the 68-
95-99.7% Rule. It tells that for a
normally distributed variable the
following are true.
Distribution Area Under The Normal Curve

z
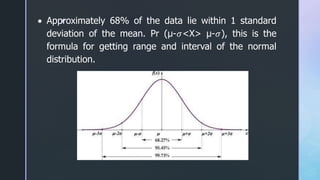
 Approximately 68% of the data lie within 1 standard
deviation of the mean. Pr (μ-𝜎<X> μ-𝜎), this is the
formula for getting range and interval of the normal
distribution.

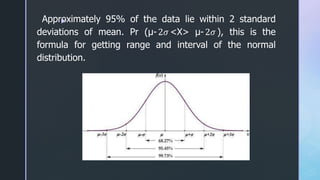
z
Approximately 95% of the data lie within 2 standard
deviations of mean. Pr (μ-2𝜎 <X> μ-2𝜎 ), this is the
distribution.

z
 Approximately 99.7% of the lie within 3 standard
deviations of the mean. Pr (μ-2𝜎<X> μ-2𝜎), this is the
distribution.

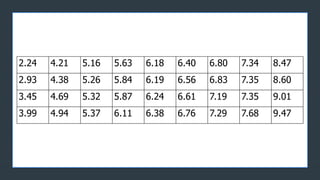
z
z
Example 1. What is the
frequency and relative
frequency of babies’
weight that are within;
a. What is the frequency
or percentage of one
standard deviation from
mean.
b. What is the frequency
or percentage of two
standard deviation from
mean.
4.94 4.69 5.26 7.29 7.19 9.47 6.61 5.84 6.83
3.45 2.93 6.38 4.38 6.76 9.02 8.47 6.80 6.40
8.60 3.99 7.68 2.24 5.32 6.24 6.29 5.63 5.37
5.26 7.35 6.11 7.34 5.87 6.56 6.18 7.35 4.21

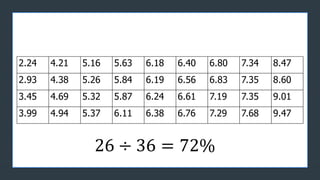
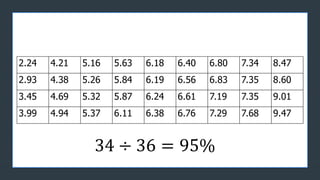
z
2.24 4.21 5.16 5.63 6.18 6.40 6.80 7.34 8.47
2.93 4.38 5.26 5.84 6.19 6.56 6.83 7.35 8.60
3.45 4.69 5.32 5.87 6.24 6.61 7.19 7.35 9.01
3.99 4.94 5.37 6.11 6.38 6.76 7.29 7.68 9.47

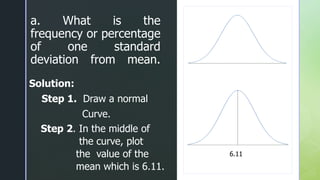
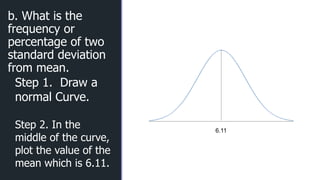
z
z
a. What is the
frequency or percentage
of one standard
deviation from mean.
Solution:
Step 1. Draw a normal
Curve.
Step 2. In the middle of
the curve, plot
the value of the
mean which is 6.11.
6.11

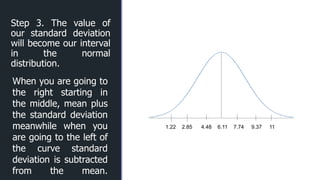
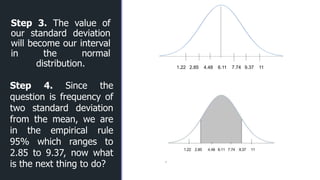
z
z
Step 3. The value of
our standard deviation
will become our interval
in the normal
distribution.
1.22 2.85 4.48 6.11 7.74 9.37 11
When you are going to
the right starting in
the middle, mean plus
the standard deviation
meanwhile when you
are going to the left of
the curve standard
deviation is subtracted
from the mean.

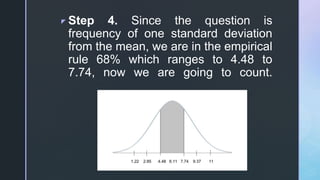
z Step 4. Since the question is
frequency of one standard deviation
from the mean, we are in the empirical
rule 68% which ranges to 4.48 to
7.74, now we are going to count.

z
2.24 4.21 5.16 5.63 6.18 6.40 6.80 7.34 8.47
2.93 4.38 5.26 5.84 6.19 6.56 6.83 7.35 8.60
3.45 4.69 5.32 5.87 6.24 6.61 7.19 7.35 9.01
3.99 4.94 5.37 6.11 6.38 6.76 7.29 7.68 9.47
26 ÷ 36 = 72%
÷÷

z
z
b. What is the
frequency or
percentage of two
standard deviation
from mean.
6.11
Step 1. Draw a
normal Curve.
Step 2. In the
middle of the curve,
plot the value of the
mean which is 6.11.

z
z
Step 3. The value of
our standard deviation
will become our interval
in the normal
distribution. 1.22 2.85 4.48 6.11 7.74 9.37 11
Step 4. Since the
question is frequency of
two standard deviation
from the mean, we are
in the empirical rule
95% which ranges to
2.85 to 9.37, now what
is the next thing to do?

z
2.24 4.21 5.16 5.63 6.18 6.40 6.80 7.34 8.47
2.93 4.38 5.26 5.84 6.19 6.56 6.83 7.35 8.60
3.45 4.69 5.32 5.87 6.24 6.61 7.19 7.35 9.01
3.99 4.94 5.37 6.11 6.38 6.76 7.29 7.68 9.47
34 ÷ 36 = 95%
÷÷

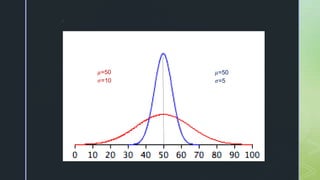
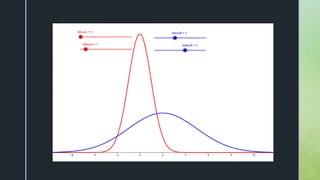
z
How about if we
compare two data
sets with normal
curve?

z
𝜇=50
𝜎=10
𝜇=50
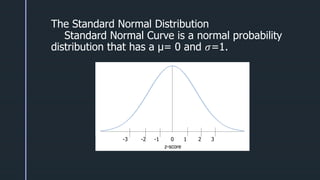
𝜎=5

z
z
The Standard Normal Distribution
Standard Normal Curve is a normal probability
distribution that has a μ= 0 and 𝜎=1.
-3 -2 -1 0 1 2 3
z-score

z The letter Z is used to denote
the standard normal random
variable. The specific value of
the random variable z is called
the z-score. The Table of Area
Under the Normal Standard
Curve is also known as the Z-
table. It is where you are going
to look for the value of random
variable z or the z-core.

z
Areas Under Normal
Curve using z-table.
z=1.09

z
z
Example. Find the area between
z=0 and z=1.54.
0.4382

z
z
Areas Under
Standard
Normal Curve
Find the area
between z=1.52
and z=2.5

z
Find the area
between z= -1.5
and z=-2.5

z
Let’s try
this !
1. Anna is planning to enroll in MSU
taking up Bachelor of Science in Civil
Engineering. The average academic
performance of all the students 80 and
a standard deviation of 5, it follows a
normal distribution.
a. Sketch a Normal Curve using
Empirical Rule and describe the
curves.
2. Find the area between z=1.7 and z=2

z
Let's have a short quiz.
Instruction: Answer the following questions and
make sure your writings clear and readable.
I. Find the area under the normal curve in
each of the following cases.
1. Find the Area between z= -1.36
and z=2.25.
2. To the right of z=1.85
3. To the left z=-0.45

z
II. Sketch a normal curve.
1. Mean of 15 and a standard deviation of 4.
On same axis, sketch another curve that has a
mean of 25 and a standard deviation of 4.
Describe the two random curves.
III. Essay
1. State a real-life situation that a normal curve
distribution can be used.

�ݺ�ߣ

NORMAL CURVE DISTRIBUTION OR BALANCE CURVE

Recommended

More Related Content

Similar to NORMAL CURVE DISTRIBUTION OR BALANCE CURVE (20)

Recently uploaded (20)

NORMAL CURVE DISTRIBUTION OR BALANCE CURVE