OIR1-L3.pptx
- 1. 1.3. Prevođenje brojeva između različitih brojnih sistema Pošto svaki broj predstavlja način za prebrojavanje elemenata nekog skupa, logično je zaključiti da za svaku vrednost postoji broj napisan u određenom brojnom sistemu koji je predstavlja. U tabeli su prikazane vrednosti od 0 do 20 predstavljene brojevima u brojnim sistemima osnove 10, 2, 8 i 16. Osnova 10 Osnova 2 Osnova 8 Osnova 16 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 17 10001 21 11 18 10010 22 12 19 10011 23 13 20 10100 24 14
- 2. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.1. Prevođenje brojeva iz brojnog sistema sa proizvoljnom osnovom u brojni sistem osnove 10 Broj napisan u bilo kom pozicionom brojnom sistemu, gde svakoj cifri odgovara određena poziciona vrednost (težina) predstavlja način za prebrojavanje elemenata nekog skupa. Ukoliko je broj napisan u brojnom sistemu koji nije dekadni, da bi stekli uvid u broj elemenata ili vrednost koju predstavlja, treba ga prevesti u dekadni brojni sistem. Primer: Binarni broj 1011 može da se predstavi kao: 1 ∗ 23 + 0 ∗ 22 + 1 ∗ 21 + 1 ∗ 20 = 8 + 0 + 2 + 1 = 11 Dakle, ukoliko se pomnoži svaka cifra sa njenom pozicionom vrednošću (težinom) i izvrši sabiranje tako dobijenih vrednosti, dobija se broj u dekadnom brojnom sistemu, koji u prethodnom primeru iznosi 11.
- 3. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.1. Prevođenje brojeva iz brojnog sistema sa proizvoljnom osnovom u brojni sistem osnove 10 Praktično prevođenje brojeva napisanih u bilo kom pozicionom brojnom sistemu u dekadni brojni sistem može se obaviti po sledećim koracima: 1. Izračunati težinu na svakoj poziciji broja stepenovanjem osnove brojnog sistema brojem (oznakom) pozicije. 2. Pomnožiti dobijenu težinu cifrom na datoj poziciji. 3. Sabrati sve dobijene vrednosti. Pri tome se sva izračunavanja obavljaju u dekadnom brojnom sistemu.
- 4. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.1. Prevođenje brojeva iz brojnog sistema sa proizvoljnom osnovom u brojni sistem osnove 10 Primer: Izračunavanje numeričke vrednosti broja 642 zapisanog u brojnom sistemu osnove 8 (zapisuje se kao 6428) može se obaviti sledeći ove korake: 6 ∗ 82 + 4 ∗ 81 + 2 ∗ 80 = 6 ∗ 64 + 4 ∗ 8 + 2 ∗ 1 = 384 + 32 + 2 = 418 (u dekadnom brojnom sistemu) Dakle, može se napisati 6428 = 41810
- 5. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.1. Prevođenje brojeva iz brojnog sistema sa proizvoljnom osnovom u brojni sistem osnove 10 Primer: Na isti način se može odrediti dekadna vrednost broja 5A7F16, zapisanog u brojnom sistemu osnove 16. 5 ∗ 163 + 𝐴 ∗ 162 + 7 ∗ 161 + 𝐹 ∗ 160 = 5 ∗ 4096 + 10 ∗ 256 + 7 ∗ 16 + 15 ∗ 1 = 2316710 (u dekadnom brojnom sistemu) Dakle, može se napisati 5A7F16 = 2316710
- 6. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.1. Prevođenje brojeva iz brojnog sistema sa proizvoljnom osnovom u brojni sistem osnove 10 Primer: Koristeći isti postupak, za binarni broj 10100110.112 određuje se njegova dekadna vrednost: 1 ∗ 27 + 0 ∗ 26 + 1 ∗ 25 + 0 ∗ 24 + 0 ∗ 23 + 1 ∗ 22 + 1 ∗ 21 + 0 ∗ 20 + 1 ∗ 2−1 + 1 ∗ 2−2 = 128 + 0 + 32 + 0 + 0 + 4 + 2 + 0 + 0.5 + 0.25 = 166.7510 (u dekadnom brojnom sistemu) Dakle, može se napisati 10100110.112 = 166.7510
- 7. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.2. Prevođenje brojeva iz dekadnog brojnog sistema u pozicioni brojni sistem sa proizvoljnom osnovom Konvertovanje celog broja iz dekadnog brojnog sistema u bilo koji drugi brojni sistem obavlja se sledećim koracima: 1. Podeliti broj napisan u dekadnom brojnom sistemu osnovom brojnog sistema u koji prevodimo. 2. Zapisati ostatak pri deljenju. 3. Dok je celobrojni deo količnika različit od nule ponavljati korake 4 i 5. 4. Celobrojni deo količnika podeliti osnovom brojnog sistema u koji prevodimo. 5. Zapisati ostatak pri deljenju s leve strane poslednjeg upisanog ostatka.
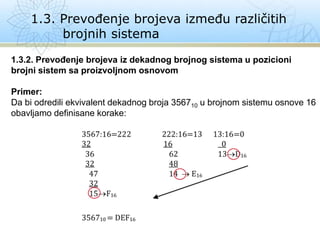
- 8. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.2. Prevođenje brojeva iz dekadnog brojnog sistema u pozicioni brojni sistem sa proizvoljnom osnovom Primer: Da bi odredili ekvivalent dekadnog broja 356710 u brojnom sistemu osnove 16 obavljamo definisane korake:
- 9. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.2. Prevođenje brojeva iz dekadnog brojnog sistema u pozicioni brojni sistem sa proizvoljnom osnovom Ukoliko se radi o realnom broju koji ima razlomljeni deo, tj. deo iza decimalne tačke, taj razlomljeni deo broja se prevodi sledećim koracima: 1. Pomnožiti razlomljeni deo broja osnovom brojnog sistema u koji prevodimo. 2. Zapisati celi deo proizvoda, kao prvu cifru razlomljenog dela broja u novom brojnom sistemu. 3. Ponavljati korake 3 i 4 dok razlomljeni deo proizvoda ne dobije vrednost 0 ili dok se ne postigne zahtevana tačnost u zapisu broja u novom brojnom sistemu 4. Razlomljeni deo proizvoda pomnožiti osnovom brojnog sistema u koji prevodimo. 5. Zapisati celi deo proizvoda s desne strane u odnosu na prethodno zapisanu cifru.
- 10. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.2. Prevođenje brojeva iz dekadnog brojnog sistema u pozicioni brojni sistem sa proizvoljnom osnovom Primer: Pri prevođenju dekadnog broja 29.77510 u binarni broj posebno se prevodi celi deo broja, a posebno razlomljeni deo broja po prethodno opisanim postupcima: Ovaj postupak nije konačan već se prevođenje u ovom primeru završava sa tačnošću do šeste decimale binarnog broja. 0.77510 = 0.1100012
- 11. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.2. Prevođenje brojeva iz dekadnog brojnog sistema u pozicioni brojni sistem sa proizvoljnom osnovom Nakon završetka ovog postupka biće određen ekvivalent dekadnog broja u traženom brojnom sistemu. Postupak prevođenja razlomljenog dela broja ne mora uvek da dâ konačan rezultat i konačan zapis u traženom brojnom sistemu, već se određuje onoliko cifara iza decimalne tačke zavisno od zahtevane tačnosti. Za prevođenje brojeva iz proizvoljnog brojnog sistema u neki drugi brojni sistem primenjuje se postupak kojim se dati broj najpre prevede u dekadni brojni sistem, a zatim iz dekadnog brojnog sistema u traženi brojni sistem.
- 12. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.3. Prevođenje brojeva iz binarnog brojnog sistema u brojni sistem čija je osnova stepen dvojke i obrnuto Pošto za osnove heksadekadnog i oktalnog brojnog sistema važi da predstavljaju odgovarajući stepen osnove binarnog brojnog sistema, tačnije, 16 = 24 i 8 = 23, prevođenje brojeva između ovih brojnih sistema u binarni brojni sistem obavlja se pojedinačnim prevođenjem svake cifre heksadekadnog, odnosno oktalnog brojnog sistema. Tako svakoj cifri heksadekadnog brojnog sistema odgovaraju četiri binarne cifre zapisane u binarnom brojnom sistemu. Primer: Prevođenje brojeva iz oktalnog i heksadekadnog u binarni A36D16 = 1010 0011 0110 11002 7248 = 111 010 1002 F12.B316 = 1111 0001 0010. 1011 00112
- 13. 1.3. Prevođenje brojeva između različitih brojnih sistema 1.3.3. Prevođenje brojeva iz binarnog brojnog sistema u brojni sistem čija je osnova stepen dvojke i obrnuto Na analogni način vrši se prevođenje brojeva iz binarnog brojnog sistema u heksadekadni i oktalni brojni sistem, grupisanjem po četiri, odnosno tri, cifre binarnog brojnog sistema i njihovim prevođenjem u heksadekadni, odnosno oktalni brojni sistem. Primer: Prevođenje brojeva iz binarnog u oktalni i heksadekadni brojni sistem 101010112 = 1010 1011 = AB16 A B 101010112 = 010 101 011 = 2538 2 5 3 1111.1012 = 001 111 . 101 = 17.58 1 7 . 5