O-net 01 а№ҖаёЈаё·а№ҲаёӯаёҮ๶ДаёӢаё• аёӮаёӯаёҮ MATH HOUSE
- 1. а№ҖаёӣпңҒаё”аёӣаёЈаё°аё•аё№аёӘаё№пңҠ O-Net аёҷпңӢаёӯаёҮа№ҶаёҷаёұаёҒа№ҖаёЈаёөаёўаёҷаёЎаёұаёҳаёўаёЎаёӣаёҘаёІаёў а№Җаё•аёЈаёөаёўаёЎаё•аёұаё§аёӘа№ҚаёІаё«аёЈаёұаёҡаё—аёөа№ҲаёҲаё°аёӘаёӯаёҡ O-Net а№ғаёҷа№Җаё”аё·аёӯаёҷ аёҒаёёаёЎаё аёІаёһаёұаёҷаёҳпңҺ аё«аёЈаё·аёӯ аёЎаёөаёҷаёІаё„аёЎ аёҒаёұаёҷаё«аёЈаё·аёӯаёўаёұаёҮ аё–пңӢаёІаёўаёұаёҮаёҘаёӯаёҮа№Җаё•аёЈаёөаёўаёЎаё•аёұаё§аёҒаёұаёҡMath House а№ғаёҷаё§аёҙаёҠаёІаё„аё“аёҙаё•аёЁаёІаёӘаё•аёЈпңҺ аёҷпңӢаёӯаёҮа№Ҷаё„аёҮไดпңӢ а№Ғаёҷаё§аё—аёІаёҮаёҒаёұаёҡ а№ӮаёҲаё—аёўпңҺа№Ғаёҷаё§ O-Net аёӯаёўпңҠаёІаёҮаёҲаёёа№ғаёҲ аёӮаёӯаёҡа№ҖаёӮаё•аёӮаёӯаёҮа№Җаёҷаё·а№үаёӯаё«аёІаё§аёҙаёҠаёІаё„аё“аёҙаё•аёЁаёІаёӘаё•аёЈпңҺ а№ғаёҷаёҒаёІаёЈаё—аё”аёӘаёӯаёҡ O-Net аёҒаёҘаёёпңҠаёЎаёӘаёІаёЈаё°аёҒаёІаёЈа№ҖаёЈаёөаёўаёҷаёЈаё№пңӢаё„аё“аёҙаё•аёЁаёІаёӘаё•аёЈпңҺ ( аё•аёІаёЎаёӘаёІаёЈаё°аёҒаёІаёЈа№ҖаёЈаёөаёўаёҷаёЈаё№пңӢа№ғаёҷаё«аёҘаёұаёҒаёӘаё№аё•аёЈаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаёӮаёұа№үаёҷаёһаё·а№үаёҷаёҗаёІаёҷ аёһ.аёЁ. 2544) 1. ๶ДаёӢаё• 1.1 аёӘаёұаёҡ๶ДаёӢаё•а№ҒаёҘаё°а№ҖаёһаёІа№Җаё§аёӯаёЈпңҺ๶ДаёӢаё• 1.2 аёўаё№а№Җаёҷаёөаёўаёҷ аёӯаёҙаёҷа№Җаё•аёӯаёЈпңҺа№ҖаёӢаёҒаёҠаёұаёҷа№ҒаёҘаё°аё„аёӯаёЎаёһаёҘаёөа№ҖаёЎаёҷаё•пңҺаёӮаёӯаёҮ๶ДаёӢаё• 2. аёҒаёІаёЈа№ғаё«пңӢа№Җаё«аё•аёёаёңаёҘа№Ғаёҡаёҡаёӯаёёаёӣаёҷаёұаёўа№ҒаёҘаё°аёҷаёҙаёЈаёҷаёұаёў 3. аёҲа№ҚаёІаёҷаё§аёҷаёҲаёЈаёҙаёҮ 3.1 аёӘаёЎаёҡаёұаё•аёҙаёҒаёІаёЈаёҡаё§аёҒа№ҒаёҘаё°аёҒаёІаёЈаё„аё№аё“аёӮаёӯаёҮаёҲа№ҚаёІаёҷаё§аёҷаёҲаёЈаёҙаёҮ 3.2 аёҒаёІаёЈа№ҒаёҒпңӢаёӘаёЎаёҒаёІаёЈаёҒа№ҚаёІаёҘаёұаёҮаёӘаёӯаёҮаё«аёҷаё¶а№ҲаёҮаё•аёұаё§а№ҒаёӣаёЈ 3.3 аё„пңҠаёІаёӘаёұаёЎаёҡаё№аёЈаё“пңҺ 3.4 аёҒаёІаёЈа№ҒаёҒпңӢаёӯаёӘаёЎаёҒаёІаёЈ 3.5 аёЈаёІаёҒаё—аёөа№Ҳn аёӮаёӯаёҮаёҲа№ҚаёІаёҷаё§аёҷаёҲаёЈаёҙаёҮ 3.6 а№ҖаёҘаёӮаёўаёҒаёҒа№ҚаёІаёҘаёұаёҮаё—аёөа№ҲаёЎаёөа№ҖаёҘаёӮаёҠаёөа№үаёҒа№ҚаёІаёҘаёұаёҮа№Җаёӣпң’аёҷаёҲа№ҚаёІаёҷаё§аёҷаё•аёЈаёЈаёҒаёўаё° 4. аё„аё§аёІаёЎаёӘаёұаёЎаёһаёұаёҷаёҳпңҺа№ҒаёҘаё°аёҹпңҗаёҮаёҒпңҺаёҠаёұаёҷ 4.1 аё„аё§аёІаёЎаёӘаёұаёЎаёһаёұаёҷаёҳпңҺа№ҒаёҘаё°аёҹпңҗаёҮаёҒпңҺаёҠаёұаёҷ 4.2 аёҹпңҗаёҮаёҒпңҺаёҠаёұаёҷа№ҖаёҠаёҙаёҮа№ҖаёӘпңӢаёҷ 4.3 аёҹпңҗаёҮаёҒпңҺаёҠаёұаёҷаёҒа№ҚаёІаёҘаёұаёҮаёӘаёӯаёҮ 4.4 аёҒаёІаёЈа№ҒаёҒпңӢаёӘаёЎаёҒаёІаёЈа№ҒаёҘаё°аёӯаёӘаёЎаёҒаёІаёЈа№Ӯаё”аёўа№ғаёҠпңӢаёҒаёЈаёІаёҹ 4.5 аёҹпңҗаёҮаёҒпңҺаёҠаёұаёҷа№ҖаёӯаёҒаёӢпңҺа№Ӯаёһа№Җаёҷаёҷа№ҖаёҠаёөаёўаёҘ 4.6 аёҹпңҗаёҮаёҒпңҺаёҠаёұаёҷаё„пңҠаёІаёӘаёұаёЎаёҡаё№аёЈаё“пңҺ 5. аёӯаёұаё•аёЈаёІаёӘпңҠаё§аёҷаё•аёЈаёөа№ӮаёҒаё“аёЎаёҙаё•аёҙ 6. аёҘа№ҚаёІаё”аёұаёҡа№ҒаёҘаё°аёӯаёҷаёёаёҒаёЈаёЎ 6.1 аёҘа№ҚаёІаё”аёұаёҡа№ҖаёҘаёӮаё„аё“аёҙаё•а№ҒаёҘаё°аёҘа№ҚаёІаё”аёұаёҡа№ҖаёЈаёӮаёІаё„аё“аёҙаё• 6.2 аёӯаёҷаёёаёҒаёЈаёЎа№ҖаёҘаёӮаё„аё“аёҙаё•а№ҒаёҘаё°аёӯаёҷаёёаёҒаёЈаёЎа№ҖаёЈаёӮаёІаё„аё“аёҙаё•
- 2. 7. аё„аё§аёІаёЎаёҷпңҠаёІаёҲаё°а№Җаёӣпң’аёҷ 7.1 аёҒаёҺа№ҖаёҒаё“аё‘пңҺа№Җаёҡаё·а№үаёӯаёҮаё•пңӢаёҷа№ҖаёҒаёөа№Ҳаёўаё§аёҒаёұаёҡаёҒаёІаёЈаёҷаёұаёҡ 7.2 аё„аё§аёІаёЎаёҷпңҠаёІаёҲаё°а№Җаёӣпң’аёҷ 8. аёӘаё–аёҙаё•аёҙ 8.1 аёӘаё–аёҙаё•аёҙа№ҒаёҘаё°аёӮпңӢаёӯаёЎаё№аёҘ 8.2 аёҒаёІаёЈа№ҒаёҲаёҒа№ҒаёҲаёҮаё„аё§аёІаёЎаё–аёөа№ҲаёӮаёӯаёҮаёӮпңӢаёӯаёЎаё№аёҘ 8.3 аёҒаёІаёЈаё§аёұаё”аё•а№ҚаёІа№Ғаё«аёҷпңҠаёҮаё—аёөа№ҲаёӮаёӯаёҮаёӮпңӢаёӯаёЎаё№аёҘ 8.4 аёҒаёІаёЈаё§аёұаё”аё„пңҠаёІаёҒаёҘаёІаёҮаёӮаёӯаёҮаёӮпңӢаёӯаёЎаё№аёҘ 8.5 аёҒаёІаёЈаё§аёұаё”аёҒаёІаёЈаёҒаёЈаё°аёҲаёІаёўаёӮаёӯаёҮаёӮпңӢаёӯаёЎаё№аёҘ 8.6 аёҒаёІаёЈаёӘа№ҚаёІаёЈаё§аёҲаё„аё§аёІаёЎаё„аёҙаё”а№Җаё«а№Үаёҷ аё•аёІаёЈаёІаёҮаё§аёҙа№Җаё„аёЈаёІаё°аё«пңҺаёӮпңӢаёӯаёӘаёӯаёҡ O-Net аёӣпңӮаёһ.аёЁ.2549 аёӣпңӮаёһ.аёЁ. 2550а№ҖаёЈаё·а№ҲаёӯаёҮ аё•аёӯаёҷаё—аёөа№Ҳ1(аёӣаёЈаёҷаёұаёў) аё•аёӯаёҷаё—аёөа№Ҳ2(аёӯаёұаё•аёҷаёұаёў) аё•аёӯаёҷаё—аёөа№Ҳ1(аёӣаёЈаёҷаёұаёў) аё•аёӯаёҷаё—аёөа№Ҳ2 (аёӣаёЈаёҷаёұаёў) 1. ๶ДаёӢаё• 2 1 2 1 2. аёҒаёІаёЈа№ғаё«пңӢа№Җаё«аё•аёёаёңаёҘа№Ғаёҡаёҡаёӯаёёаёӣаёҷаёұаёўа№ҒаёҘаё° аёҷаёҙаёЈаёҷаёұаёў 1 - - 1 3. аёҲа№ҚаёІаёҷаё§аёҷаёҲаёЈаёҙаёҮа№ҒаёҘаё°а№ҖаёҘаёӮаёўаёҒаёҒа№ҚаёІаёҘаёұаёҮ 6 1 6 4 4. аё„аё§аёІаёЎаёӘаёұаёЎаёһаёұаёҷаёҳпңҺа№ҒаёҘаё°аёҹпңҗаёҮаёҒпңҺаёҠаёұаёҷ 4 2 2 3 5. аёӯаёұаё•аёЈаёІаёӘпңҠаё§аёҷаё•аёЈаёөа№ӮаёҒаё“аёЎаёҙаё•аёҙ 3 2 1 2 6. аёҘа№ҚаёІаё”аёұаёҡа№ҒаёҘаё°аёӯаёҷаёёаёҒаёЈаёЎ 6 - 2 2 7. аё„аё§аёІаёЎаёҷпңҠаёІаёҲаё°а№Җаёӣпң’аёҷ 1 3 1 2 8. аёӘаё–аёҙаё•аёҙ 9 1 6 5 аё«аёЎаёІаёўа№Җаё«аё•аёё : аёӮпңӢаёӯаёӘаёӯаёҡаё•аёӯаёҷаё—аёөа№Ҳ 2 1) аёӣпңӮаёһ.аёЁ. 2549 а№Җаёӣпң’аёҷаёӮпңӢаёӯаёӘаёӯаёҡа№Җаё•аёҙаёЎаё„а№ҚаёІаё•аёӯаёҡ 2) аёӣпңӮаёһ.аёЁ. 2550 а№Җаёӣпң’аёҷаёӮпңӢаёӯаёӘаёӯаёҡа№Ғаёҡаёҡа№ҖаёҘаё·аёӯаёҒаё•аёӯаёҡ
- 3. аёӘаёЈаёёаёӣаёӣаёЈаё°а№Җаё”а№ҮаёҷаёӘа№ҚаёІаё„аёұаёҚа№Җаё•аёЈаёөаёўаёЎаёӘаёӯаёҡ O-Net а№ҖаёЈаё·а№ҲаёӯаёҮ ๶ДаёӢаё• аёЈаё§аёҡаёЈаё§аёЎа№Ӯаё”аёў аёӯаёІаёҲаёІаёЈаёўпңҺаёӘаёЎаёҡаё№аёЈаё“пңҺ аёҘаёұаёҒаё©аё“аё°аё§аёҙаёЎаёҘ аёӯаёІаёҲаёІаёЈаёўпңҺаёӣаёЈаё°аёҲа№ҚаёІ аёӘаёІаёӮаёІаёһаёЈаё°аёЈаёІаёЎаёӘаёӯаёҮ 1 аё–пңӢаёІ A аёЎаёөаёӘаёЎаёІаёҠаёҙаёҒ n аё•аёұаё§ аёӘаёұаёҡ๶ДаёӢаё•аёӮаёӯаёҮ A аё—аёұа№үаёҮаё«аёЎаё” = 2n ๶ДаёӢаё• а№ҒаёҘаё° аёӘаёұаёҡ๶ДаёӢаё•а№Ғаё—пңӢ = 2n вҖ“ 1 ๶ДаёӢаё• 2 аёҒаёІаёЈаёҒаёЈаё°аё—а№ҚаёІаёӮаёӯаёҮ๶ДаёӢаё• AвҲӘB = { x | x вҲҲAвҲЁ xвҲҲB} AвҲ©B = { x | x вҲҲA вҲ§ xвҲҲB} A вҖ“ B = { x | x вҲҲA вҲ§ xвҲүB} AвҖІ = { x | x вҲҲU вҲ§ xвҲүA} 3 аё„аёёаё“аёӘаёЎаёҡаёұаё•аёҙаё—аёөа№Ҳаё•пңӢаёӯаёҮаё—аёЈаёІаёҡ (1) P(A) вҲӘP(B)вҠӮP(AвҲӘB) а№ҒаёҘаё° (2) P(A) вҲ©P(B) = P(AвҲ©B) (3) AвҲ© (BвҲӘC) = (AвҲ©B) вҲӘ (AвҲ©C) (4) A вҲӘ (BвҲ©C) = (AвҲӘB)вҲ© (AвҲӘC) (5) (AвҲ©B)вҖІ = AвҖІвҲӘBвҖІ , (AвҲӘB)вҖІ = AвҖІвҲ©BвҖІ (6) A вҖ“ B = A вҲ©BвҖІ = BвҖІвҖ“ AвҖІ (7) AвҲ© (AвҲӘB) = A , A вҲӘ (AвҲ©B) = A (8) AвҲ© (AвҖІвҲӘB) = AвҲ©B (9) AвҲӘ (AвҖІвҲ©B) = AвҲӘB (10)(AвҲӘB)вҲ© (AвҲӘBвҖІ) = A (11)(AвҲ©B) вҲӘ (AвҲ©BвҖІ) = A 4 аёҲа№ҚаёІаёҷаё§аёҷаёӘаёЎаёІаёҠаёҙаёҒаёӮаёӯаёҮ๶ДаёӢаё• n (AвҲӘBвҲӘC) = n(A) + n(B) + n(C) вҖ“ n(AвҲ©B) вҖ“ n(AвҲ©C) вҖ“ n(BвҲ©C) + n(AвҲ©BвҲ©C)
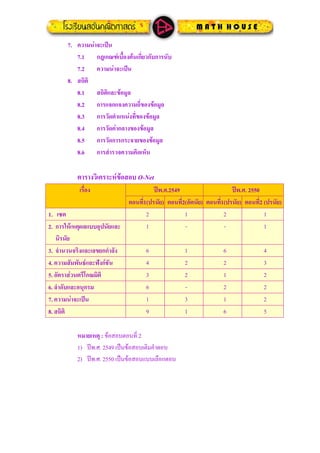
- 4. 5 аёӘаёЎаёҡаёұаё•аёҙа№ҖаёҒаёөа№Ҳаёўаё§аёҒаёұаёҡ๶ДаёӢаё•аё—аёөа№Ҳаё«пңӢаёІаёЎаёҘаё·аёЎ (1) аёӘаёЎаёҡаёұаё•аёҙа№ҖаёҒаёөа№Ҳаёўаё§аёҒаёұаёҡаёӘаёұаёҡ๶ДаёӢаё• AвҠӮB аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ AвҲ©B = A AвҠӮB аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ AвҲӘB = B AвҠӮB аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ BвҖІвҠӮAвҖІ (2) аёӘаёЎаёҡаёұаё•аёҙа№ҖаёҒаёөа№Ҳаёўаё§аёҒаёұаёҡаёҒаёІаёЈаёҒаёЈаё°аё—а№ҚаёІ AвҲӘB = ПҶ аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ A= ПҶ а№ҒаёҘаё° B= ПҶ AвҲ©B = ПҶ аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ AвҠӮBвҖІ а№ҒаёҘаё° BвҠӮAвҖІ AвҖ“ B = ПҶ аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ AвҠӮB (3) аёӘаёЎаёҡаёұаё•аёҙаёӮаёӯаёҮа№ҖаёһаёІа№Җаё§аёӯаёЈпңҺ๶ДаёӢаё• а№ҖаёЎаё·а№Ҳаёӯ A , B а№Җаёӣпң’аёҷ๶ДаёӢаё•а№ғаё” а№Ҷ 1.) x вҲҲP(A) вҶ” xвҠӮA 2.) ПҶ вҲҲ P(A) а№ҒаёҘаё° AвҲҲ P(A) 3.) ПҶ вҠӮ P(A) , {ПҶ}вҠӮ P(A) а№ҒаёҘаё° {A} вҠӮ P(A) 4.) аё–пңӢา๶ДаёӢаё• A аёЎаёөаёӘаёЎаёІаёҠаёҙаёҒ n аё•аёұаё§ а№ҒаёҘпңӢаё§ P(A) аёЎаёөаёӘаёЎаёІаёҠаёҙаёҒ 2n аё•аёұаё§ (4) а№ғаё«пңӢ A = {1 , 2 , 3 , вҖҰ , m} а№ҒаёҘаё° B = { 1 , 2 , 3 , вҖҰ , n} а№Ӯаё”аёўаё—аёөа№Ҳ m < n 1.) аё–пңӢаёІ AвҠӮ XвҠӮB аёҲаё°аёЎаёө๶ДаёӢаё• X ไดпңӢ = 2n-m ๶ДаёӢаё• 2.) аё–пңӢаёІ A вҲ© X вү ПҶ а№ҒаёҘаё° X вҠӮB аёҲаё°аёЎаёө๶ДаёӢаё• X ไดпңӢ = 2n вҖ“ 2n-m ๶ДаёӢаё• (5) n(A вҖ“ B) = n(A) вҖ“ n(AвҲ©B) (6) n(AвҲӘB) вҖІ = n(U) вҖ“ n(AвҲӘB) (7) n[P(A) вҖ“ P(B)] = n[P(A)] вҖ“ n[P(AвҲ©B)]
- 5. а№Ғаёҷаё§аёӮпңӢаёӯаёӘаёӯаёҡа№ҖаёЈаё·а№ҲаёӯаёҮ ๶ДаёӢаё• аёЈаё§аёҡаёЈаё§аёЎа№Ӯаё”аёў аёӯаёІаёҲаёІаёЈаёўпңҺаёӘаёЎаёҡаё№аёЈаё“пңҺ аёҘаёұаёҒаё©аё“аё°аё§аёҙаёЎаёҘ аёӯаёІаёҲаёІаёЈаёўпңҺаёӣаёЈаё°аёҲа№ҚаёІ аёӘаёІаёӮаёІаёһаёЈаё°аёЈаёІаёЎаёӘаёӯаёҮ аёҒа№ҚаёІаё«аёҷаё” A , B , C а№ҒаёҘаё° D а№Җаёӣпң’аёҷ๶ДаёӢаё•а№ғаё”а№Ҷ (AвҲ©B) вҖ“ (CвҲӘD) а№Җаё—пңҠаёІаёҒаёұаёҡ๶ДаёӢаё•а№ғаёҷаёӮпңӢаёӯа№ғаё”1. 1. (A вҖ“ B) вҲ© (C вҖ“ D) 2. (A вҖ“ B) вҲ© (D вҖ“ C) 3. (A вҖ“ C) вҲ© (B вҖ“ D) 4. (A вҖ“ C) вҲ© (D вҖ“ B) а№Ғаёҷаё§аё„аёҙаё” (AвҲ©B) вҖ“ (CвҲӘD) = (AвҲ©B) вҲ© (CвҲӘDQ )вҖІ = (AвҲ©B) вҲ© (CвҖІвҲ©DвҖІ) = (AвҲ©CвҖІ) вҲ© (B вҲ©DвҖІ) вҲҙ(AвҲ©B) вҖ“ (CвҲӘD) = (A вҖ“ C) вҲ© (B - D) 2. аёҒа№ҚаёІаё«аёҷаё” A а№ҒаёҘаё° B а№Җаёӣпң’аёҷ๶ДаёӢаё•а№ғаё”а№Ҷ аёҲаёҮаёһаёҙаёҲаёІаёЈаё“аёІаёӮпңӢаёӯаё„аё§аёІаёЎаё•пңҠаёӯไаёӣаёҷаёөа№ү аёҒ. аё–пңӢаёІ AвҲ©B = ПҶ а№ҒаёҘпңӢаё§ A вҠӮBвҖІ аёӮ. аё–пңӢаёІ AвҲ©B = ПҶ а№ҒаёҘпңӢаё§ B вҠӮAвҖІ вҖІ аёӮпңӢаёӯа№ғаё”аёӘаёЈаёёаёӣаё–аё№аёҒаё•пңӢаёӯаёҮ 1. аёҒ. аё–аё№аёҒ а№ҒаёҘаё° аёӮ аёңаёҙаё” 2. аёҒ. аёңаёҙаё” а№ҒаёҘаё° аёӮ. аё–аё№аёҒ 3. аёҒ. а№ҒаёҘаё° аёӮ. аё–аё№аёҒ 4. аёҒ. а№ҒаёҘаё° аёӮ. аёңаёҙаё” а№Ғаёҷаё§аё„аёҙаё” а№Җаёҷаё·а№ҲаёӯаёҮаёҲаёІаёҒ AвҲ©B = ПҶ аёһаёҙаёҲаёІаёЈаё“аёІа№Ғаёңаёҷаё аёІаёһаё”аёұаёҮаёҷаёөа№ү A B A B A B аёҲаё°аёһаёҡаё§пңҠаёІ A вҠӮ B а№Ғаё•пңҠ B вҠ„вҖІ вҖІ AвҖІ
- 6. 3. аёҒа№ҚаёІаё«аёҷаё” A = {0, {0}, ПҶ, {ПҶ}, 1} а№ҒаёҘаё° P(A) а№Җаёӣпң’аёҷа№ҖаёһаёІа№Җаё§аёӯаёЈпңҺ๶ДаёӢаё•аёӮаёӯаёҮ A аёҲа№ҚаёІаёҷаё§аёҷаёӘаёЎаёІаёҠаёҙаёҒаёӮаёӯаёҮ P(A) вҖ“ A а№Җаё—пңҠаёІаёҒаёұаёҡа№Җаё—пңҠаёІа№ғаё” 1. 29 2. 30 3. 31 4. 32 а№Ғаёҷаё§аё„аёҙаё” n(A) = 5Q аёҲะไดпңӢ n(P(A)) = 25 = 32 вҺҜ 1 а№Ғаё•пңҠ A а№ҒаёҘаё° P(A) аёЎаёөаёӘаёЎаёІаёҠаёҙаёҒаёӢа№үа№ҚаёІаёҒаёұаёҷ 3 аё•аёұаё§аё„аё·аёӯ {0}, ПҶ, {ПҶ} вҲҙ n(P(A) вҲ© A) = 3 вҺҜ 2 а№Җаёҷаё·а№ҲаёӯаёҮаёҲаёІаёҒ n[P(A) вҖ“ A] = n(P(A)) вҖ“ n(P(A) вҲ© A) аё”аёұаёҮаёҷаёұа№үаёҷ n[P(A) вҖ“ A] = 32 вҖ“ 3 = 29 аё•аёұаё§ аёҒа№ҚаёІаё«аёҷаё”а№ғаё«пңӢ A а№ҒаёҘаё° B а№Җаёӣпң’аёҷ๶ДаёӢаё•аёҲа№ҚаёІаёҒаёұаё”а№Ӯаё”аёўаё—аёөа№Ҳ n(A вҲӘ B) = 67 а№ҒаёҘаё° n[(A вҖ“ B)вҲӘ(B вҖ“ A)] = 584. аё–пңӢаёІ n(A) = 32 а№ҒаёҘпңӢаё§ n(B) аёЎаёөаё„пңҠаёІа№Җаё—пңҠаёІаёҒаёұаёҡаёӮпңӢаёӯа№ғаё”аё•пңҠаёӯไаёӣаёҷаёөа№ү 1. 28 2. 35 3. 39 4. 44 а№Ғаёҷаё§аё„аёҙаё” аёҲаёІаёҒа№Ғаёңаёҷаё аёІаёһа№Җаё§аёҷаёҷпңҺ вҖ“ аёӯаёӯаёўа№ҖаёҘаёӯаёЈпңҺ аёҲаё°аёһаёҡаё§пңҠаёІ n(A вҲӘ B) = n[(A вҖ“ B) вҲӘ (B вҖ“ A)] + n(AвҲ©B) а№Ғаё—аёҷаё„пңҠаёІаёҲะไดпңӢ 67 = 58 + n(A вҲ©B) A B U A - B B - A AвҲ©B вҲҙ n(A вҲ©B) = 67 вҖ“ 58 = 9 вҺҜ вҲ— а№Җаёҷаё·а№ҲаёӯаёҮаёҲаёІаёҒ n(A вҲӘ B) = n(A) + n(B) - n(A вҲ© B) аёҲะไดпңӢ 67 = 32 + n(B) вҖ“ 9 аё”аёұаёҮаёҷаёұа№үаёҷ n(B) = 67 вҖ“ 32 + 9 = 44
- 7. аёӮпңӢаёӯа№ғаё”аё•пңҠаёӯไаёӣаёҷаёөа№үไมпңҠаё–аё№аёҒаё•пңӢаёӯаёҮ5. 1. аёЎаёө๶ДаёӢаё•аёҡаёІаёҮ๶ДаёӢตไมпңҠаёЎаёөаёӘаёұаёҡ๶ДаёӢаё•а№Ғаё—пңӢ аё–пңӢаёІ A = {1, {1, 2}, ПҶ} а№ҒаёҘпңӢаё§ A вҲ© P(A) вү ПҶ2. 3. P(ПҶ)вҲ© P(P(ПҶ)) = ПҶ 4. аёЎаёө๶ДаёӢаё• A аё—аёөа№Ҳаё—а№ҚаёІа№ғаё«пңӢаёҲа№ҚаёІаёҷаё§аёҷаёӘаёЎаёІаёҠаёҙаёҒаёӮаёӯаёҮ P(A) а№Җаёӣпң’аёҷаёҲа№ҚаёІаёҷаё§аёҷа№ҖаёүаёһаёІаё° а№Ғаёҷаё§аё„аёҙаё” аёһаёҙаёҲаёІаёЈаё“аёІа№Ғаё•пңҠаёҘаё°аёӮпңӢаёӯаё”аёұаёҮаёҷаёөа№ү аёӮпңӢаёӯ1 аё–аё№аёҒаё•пңӢаёӯаёҮ а№ҖаёһаёЈаёІаё°аё§пңҠаёІ аё–пңӢаёІ A = ПҶ аёҲаё°аёһаёҡаё§пңҠаёІаёӘаёұаёҡ๶ДаёӢаё•аёӮаёӯаёҮ A аё„аё·аёӯ ПҶ аёӢаё¶а№ҲаёҮไมпңҠа№ғаёҠпңҠаёӘаёұаёҡ๶ДаёӢаё•а№Ғаё—пңӢ аёӮпңӢаёӯ2 аё–аё№аёҒаё•пңӢаёӯаёҮ а№ҖаёһаёЈаёІаё°аё§пңҠаёІ A = {1, {1, 2}, ПҶ} аёҲะไดпңӢ P(A) = {ПҶ, {1}, {{1, 2}}, {ПҶ}, {1,{1, 2}}, {1, ПҶ}, {{1, 2}, ПҶ}, {1,{1, 2}, ПҶ}} аёҲаё°аёһаёҡаё§пңҠаёІ A вҲ© P(A) = {ПҶ} вү ПҶ аёӮпңӢаёӯ3 ไมпңҠаё–аё№аёҒаё•пңӢаёӯаёҮ а№ҖаёһаёЈаёІаё°аё§пңҠаёІ P(ПҶ) = {ПҶ} P(P(ПҶ)) = {ПҶ, {ПҶ}} аё”аёұаёҮаёҷаёұа№үаёҷ P(ПҶ)вҲ©P(P(ПҶ) = {ПҶ} вү ПҶ аёӮпңӢаёӯ4 аё–аё№аёҒаё•пңӢаёӯаёҮ а№ҖаёһаёЈаёІаё°аё§пңҠаёІ аё–пңӢаёІ A = {1} вҶ’ A аёЎаёөаёӘаёЎаёІаёҠаёҙаёҒ 1 аё•аёұаё§ вҲҙ P(A) аёЎаёөаёӘаёЎаёІаёҠаёҙаёҒ = 2 = 2 аё•аёұаё§ а№ҒаёӘаё”аёҮаё§пңҠаёІ аёҲа№ҚаёІаёҷаё§аёҷаёӘаёЎаёІаёҠаёҙаёҒа№Җаёӣпң’аёҷаёҲа№ҚаёІаёҷаё§аёҷа№ҖаёүаёһаёІаё° а№ғаё«пңӢа№ҖаёӯаёҒаё аёһаёӘаёұаёЎаёһаёұаё—аёҳпңҺ U = {1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9} аё–пңӢаёІ A вҲӘ B = {1 , 2 , 3 , 4 , 5 , 6 , 7}6. а№ҒаёҘаё° = {4 , 6 , 8 , 9} аёҲа№ҚаёІаёҷаё§аёҷаёӘаёЎаёІаёҠаёҙаёҒаёӮаёӯаёҮ B вҖ“ A а№Җаё—пңҠаёІаёҒаёұаёҡаёӮпңӢаёӯа№ғаё”AвҖІ 1. 1 2. 2 3. 3 4. 4 а№Ғаёҷаё§аё„аёҙаё” аёҲаёІаёҒ U = {1 , 2 , 3 , 4 , 5 , 6 , 7, 8 , 9} а№ҒаёҘаё° = {4 , 6 , 8 , 9}AвҖІ аёҲะไดпңӢ A = {1 , 2 , 3 , 5 , 7} вҺҜвҲ— аёҲаёІаёҒ A вҲӘ B = {1 , 2 , 3 , 4 , 5 , 6 , 7} аёҲะไดпңӢ B вҖ“ A = {4 , 6} вҺҜвҲ— аё”аёұаёҮаёҷаёұа№үаёҷ B вҖ“ A аёЎаёөаёӘаёЎаёІаёҠаёҙаёҒ 2 аё•аёұаё§
- 8. 7. аёҲаёІаёҒаёҒаёІаёЈаёӘаёұаёЎаё аёІаё©аё“пңҺаёңаё№пңӢаёҠаёЎаёЈаёІаёўаёҒаёІаёЈа№Ӯаё—аёЈаё—аёұаёЁаёҷпңҺаёҲа№ҚаёІаёҷаё§аёҷ 220 аё„аёҷ аёһаёҡаё§пңҠаёІ аёЎаёө 140 аё„аёҷ аёҠаёӯаёҡаё”аё№аёЈаёІаёўаёҒаёІаёЈ вҖңа№ҖаёҒаёЎаёӘпңҺа№ӮаёҠаё§пңҺвҖқ аёЎаёө 110 аё„аёҷ аёҠаёӯаёҡаё”аё№аёЈаёІаёўаёҒаёІаёЈ вҖңа№ҖаёҒаёЎаёӘпңҺа№ҖаёЁаёЈаё©аёҗаёөвҖқ аёЎаёө 105 аё„аёҷ аёҠаёӯаёҡаё”аё№аёЈаёІаёўаёҒаёІаёЈ вҖңаё•аёөаёӘаёҙаёҡвҖқ аёЎаёө 45 аё„аёҷ аёҠаёӯаёҡаё”аё№аё—аёұа№үаёҮаёЈаёІаёўаёҒаёІаёЈ вҖңа№ҖаёҒаёЎаёӘпңҺа№ӮаёҠаё§пңҺвҖқ а№ҒаёҘаё° вҖңаё•аёөаёӘаёҙаёҡвҖқ аёЎаёө 40 аё„аёҷ аёҠаёӯаёҡаё”аё№аё—аёұа№үаёҮаёЈаёІаёўаёҒаёІаёЈ вҖңа№ҖаёҒаёЎаёӘпңҺа№ӮаёҠаё§пңҺвҖқ а№ҒаёҘаё° вҖңа№ҖаёҒаёЎаёӘпңҺа№ҖаёЁаёЈаё©аёҗаёөвҖқ аёЎаёө 15 аё„аёҷ аёҠаёӯаёҡаё”аё№аё—аёұа№үаёҮаёӘаёІаёЎаёЈаёІаёўаёҒаёІаёЈ аё–пңӢาไมпңҠаёЎаёөаёңаё№пңӢаёҠаёЎаё„аёҷа№ғаё”аё—аёөа№ҲไมпңҠаёҠаёӯаёҡаё”аё№аё—аёұа№үаёҮаёӘаёІаёЎаёЈаёІаёўаёҒаёІаёЈа№ҖаёҘаёў аёҲаёҮаё«аёІаёҲа№ҚаёІаёҷаё§аёҷаёңаё№пңӢаёҠаёЎаёЈаёІаёўаёҒаёІаёЈа№Ӯаё—аёЈаё—аёұаёЁаёҷпңҺаё—аёөа№ҲаёҠаёӯаёҡаё”аё№ аёЈаёІаёўаёҒаёІаёЈаё”аёұаёҮаёҒаёҘпңҠаёІаё§аёӯаёўпңҠаёІаёҮаёҷпңӢаёӯаёўаёӘаёӯаёҮаёЈаёІаёўаёҒаёІаёЈ 1. 80 аё„аёҷ 2. 110 аё„аёҷ 3. 120 аё„аёҷ 4. 130 аё„аёҷ а№Ғаёҷаё§аё„аёҙаё” а№ғаё«пңӢ A а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаёңаё№пңӢаёҠаёЎаёЈаёІаёўаёҒаёІаёЈ вҖңа№ҖаёҒаёЎаёӘпңҺа№ӮаёҠаё§пңҺвҖқ вҲҙn(A) = 140 B а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаёңаё№пңӢаёҠаёЎаёЈаёІаёўаёҒаёІаёЈ вҖңа№ҖаёҒаёЎаёӘпңҺа№ҖаёЁаёЈаё©аёҗаёөвҖқ вҲҙn(B) = 110 C а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаёңаё№пңӢаёҠаёЎаёЈаёІаёўаёҒаёІаёЈ вҖңаё•аёөаёӘаёҙаёҡвҖқ вҲҙn(C) = 105 аёҲะไดпңӢ n(AвҲ© B) = 40, n(A вҲ© C) = 45, n(AвҲ©BвҲ©C) = 15 а№ҖаёӮаёөаёўаёҷа№Ғаёңаёҷаё аёІаёһไดпңӢаё”аёұаёҮаёЈаё№аёӣ 15 A(140) B(110) U(220) 25 C(105) 30 a b c аёҲаёІаёҒа№Ғаёңаёҷаё аёІаёһ a + b + c = 80 а№Ғаё•пңҠ a + b = 70 вҲҙ c = 10 аёҲะไดпңӢ b = n(C) вҖ“ c вҖ“ 30 вҖ“ 15 = 105 вҖ“ 10 вҖ“ 45 = 50 аё”аёұаёҮаёҷаёұа№үаёҷ аёңаё№пңӢаёҠаёЎаёЈаёІаёўаёҒаёІаёЈа№Ӯаё—аёЈаё—аёұаёЁаёҷпңҺаё—аёөа№ҲаёҠаёӯаёҡаё”аё№аёЈаёІаёўаёҒаёІаёЈаёӯаёўпңҠаёІаёҮаёҷпңӢаёӯаёўаёӘаёӯаёҮаёЈаёІаёўаёҒаёІаёЈа№Җаё—пңҠаёІаёҒаёұаёҡ 30 + 15 + 25 + 50 = 120 аё„аёҷ
- 9. 8. аёҲаёІаёҒаёҒаёІаёЈаёӘа№ҚаёІаёЈаё§аёҲаёҒаёІаёЈаёӣаёЈаё°аёҒаёӯаёҡаёӯаёІаёҠаёөаёһаёҒаёІаёЈаёӣаёЈаё°аёЎаёҮаё—а№ҚаёІаёӘаё§аёҷаёўаёІаёҮаёһаёІаёЈаёІа№ҒаёҘаё°аё—а№ҚаёІаёӘаё§аёҷаёңаёҘไมпңӢаёӮаёӯаёҮаёҠаёІаё§аёҡпңӢаёІаёҷа№ғаёҷ аё«аёЎаё№пңҠаёҡпңӢаёІаёҷа№Ғаё«пңҠаёҮаё«аёҷаё¶а№ҲаёҮаёӮаёӯаёҮаёҲаёұаёҮаё«аё§аёұаё”аёЈаё°аёўаёӯаёҮ аёӢаё¶а№ҲаёҮаёЎаёөаёӯаёўаё№пңҠаё—аёұа№үаёҮаё«аёЎаё” 108 аё„аёЈаёӯаёҡаё„аёЈаёұаё§аёһаёҡаё§пңҠаёІ аёЎаёө 38 аё„аёЈаёӯаёҡаё„аёЈаёұаё§ ไมпңҠไดпңӢаёӣаёЈаё°аёҒаёӯаёҡаёӯаёІаёҠаёөаёһаё—аёұа№үаёҮаёӘаёІаёЎаёҷаёөа№ү аёЎаёө 16 аё„аёЈаёӯаёҡаё„аёЈаёұаё§ аё—аёөа№ҲаёӣаёЈаё°аёҒаёӯаёҡаёӯаёІаёҠаёөаёһаё—аёұа№үаёҮаёӘаёІаёЎаёҷаёөа№ү аёЎаёө 29 аё„аёЈаёӯаёҡаё„аёЈаёұаё§ аё—аёөа№ҲаёӣаёЈаё°аёҒаёӯаёҡаёӯаёІаёҠаёөаёһа№ҖаёһаёөаёўаёҮаёӯаёўпңҠаёІаёҮа№Җаё”аёөаёўаё§а№ғаёҷаёӘаёІаёЎаёӯаёўпңҠаёІаёҮаёҷаёөа№ү аёӮпңӢаёӯа№ғаё”аё•пңҠаёӯไаёӣаёҷаёөа№үа№Җаёӣпң’аёҷаёҲа№ҚаёІаёҷаё§аёҷаё„аёЈаёӯаёҡаё„аёЈаёұаё§аё—аёөа№ҲаёӣаёЈаё°аёҒаёӯаёҡаёӯаёІаёҠаёөаёһаёӯаёўпңҠаёІаёҮаёҷпңӢаёӯаёўаёӘаёӯаёҮа№ғаёҷаёӘаёІаёЎаёӯаёўпңҠаёІаёҮаёҷаёөа№ү 1. 25 2. 41 3. 45 4. 63 а№Ғаёҷаё§аё„аёҙаё” а№ғаё«пңӢ U а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаё„аёЈаёӯаёҡаё„аёЈаёұаё§аё—аёұа№үаёҮаё«аёЎаё” вҲҙn(U) = 108 A а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаё„аёЈаёӯаёҡаё„аёЈаёұаё§аё—аёөа№ҲไมпңҠไดпңӢаёӣаёЈаё°аёҒаёӯаёҡаёӯаёІаёҠаёөаёһаёҷаёөа№ү вҲҙn(A) = 38 B а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаё„аёЈаёӯаёҡаё„аёЈаёұаё§аё—аёөа№ҲаёӣаёЈаё°аёҒаёӯаёҡаёӯаёІаёҠаёөаёһаёҷаёөа№ү 1 аёӯаёўпңҠаёІаёҮ вҲҙn(B) = 29 C а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаё„аёЈаёӯаёҡаё„аёЈаёұаё§аё—аёөа№ҲаёӣаёЈаё°аёҒаёӯаёҡаёӯаёІаёҠаёөаёһаёҷаёөа№үаёӯаёўпңҠаёІаёҮаёҷпңӢаёӯаёў 2 а№ғаёҷ 3 аёӯаёўпңҠаёІаёҮаёҷаёөа№ү аёҲะไดпңӢ n(U) = n(A) + n(B) + n(C) вҲҙ n(C) = 108 вҖ“ 38 - 29 = 41 аё”аёұаёҮаёҷаёұа№үаёҷ аёҲа№ҚаёІаёҷаё§аёҷаё„аёЈаёӯаёҡаё„аёЈаёұаё§аё—аёөа№ҲаёӣаёЈаё°аёҒаёӯаёҡаёӯаёІаёҠаёөаёһаёӯаёўпңҠаёІаёҮаёҷпңӢаёӯаёўаёӘаёӯаёҮа№ғаёҷаёӘаёІаёЎаёӯаёўпңҠаёІаёҮаёҷаёөа№үа№Җаё—пңҠаёІаёҒаёұаёҡ 41 аё„аёЈаёӯаёҡаё„аёЈаёұаё§ 9. аёҷаёұаёҒаёҒаёІаёЈа№ҖаёЎаё·аёӯаёҮаёҒаёҘаёёпңҠаёЎаё«аёҷаё¶а№ҲаёҮаёЎаёө 50 аё„аёҷ а№Ғаё•пңҠаёҘаё°аё„аёҷаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё”пңӢаёІаёҷаё§аёҙаё—аёўаёІаёЁаёІаёӘаё•аёЈпңҺаё«аёЈаё·аёӯаёӘаёұаёҮаё„аёЎаёЁаёІаёӘаё•аёЈпңҺ аё«аёЈаё·аёӯаёЁаёҙаёҘаёӣаёЁаёІаёӘаё•аёЈпңҺаёӯаёўпңҠаёІаёҮаёҷпңӢаёӯаёўаё«аёҷаё¶а№ҲаёҮаё”пңӢаёІаёҷ аёҲаёІаёҒа№ҒаёҹпңҶаёЎаёӣаёЈаё°аё§аёұаё•аёҙаёһаёҡаёӯаёөаёҒаё§пңҠаёІаёЎаёө 33 аё„аёҷ аё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІ аё”пңӢаёІаёҷаёӘаёұаёҮаё„аёЎаёЁаёІаёӘаё•аёЈпңҺа№ҒаёҘаё°а№ғаёҷаёҲа№ҚаёІаёҷаё§аёҷаёҷаёөа№үаёЎаёө 8 аё„аёҷ аё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё—аёІаёҮаё”пңӢаёІаёҷаё§аёҙаё—аёўаёІаёЁаёІаёӘаё•аёЈпңҺаё”пңӢаё§аёў аёЎаёө 17 аё„аёҷ аё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё—аёІаёҮаё”пңӢаёІаёҷаёЁаёҙаёҘаёӣаёЁаёІаёӘаё•аёЈпңҺа№ҒаёҘаё°а№ғаёҷаёҲа№ҚаёІаёҷаё§аёҷаёҷаёөа№үаёЎаёө 2 аё„аёҷ аё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷ аёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё—аёІаёҮаё”пңӢаёІаёҷаё§аёҙаё—аёўаёІаёЁаёІаёӘаё•аёЈпңҺаё”пңӢаё§аёў аё–пңӢาไมпңҠаёӣаёЈаёІаёҒаёҸаё§пңҠаёІаёЎаёөаёңаё№пңӢаё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё—аёұа№үаёҮаё”пңӢаёІаёҷаёӘаёұаёҮаё„аёЎаёЁаёІаёӘаё•аёЈпңҺ а№ҒаёҘаё°аёЁаёҙаёҘаёӣаёЁаёІаёӘаё•аёЈпңҺа№ҒаёҘпңӢаё§ аёҷаёұаёҒаёҒаёІаёЈа№ҖаёЎаё·аёӯаёҮаё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё”пңӢаёІаёҷаё§аёҙаё—аёўаёІаёЁаёІаёӘаё•аёЈпңҺаёЎаёөаёҒаёөа№Ҳаё„аёҷ 1. 25 аё„аёҷ 2. 20 аё„аёҷ 3. 18 аё„аёҷ 4. 10 аё„аёҷ а№Ғаёҷаё§аё„аёҙаё” а№ғаё«пңӢ A а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаёҷаёұаёҒаёҒаёІаёЈа№ҖаёЎаё·аёӯаёҮаё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё”пңӢаёІаёҷаё§аёҙаё—аёўаёІаёЁаёІаёӘаё•аёЈпңҺ B а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаёҷаёұаёҒаёҒаёІаёЈа№ҖаёЎаё·аёӯаёҮаё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё”пңӢаёІаёҷаёӘаёұаёҮаё„аёЎаёЁаёІаёӘаё•аёЈпңҺ C а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаёҷаёұаёҒаёҒаёІаёЈа№ҖаёЎаё·аёӯаёҮаё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё”пңӢаёІаёҷаёЁаёҙаёҘаёӣаёЁаёІаёӘаё•аёЈпңҺ
- 10. а№ҖаёӮаёөаёўаёҷа№Ғаёңаёҷаё аёІаёһа№Җаё§аёҷаёҷпңҺ вҖ“ аёӯаёӯаёўа№ҖаёҘаёӯаёЈпңҺไดпңӢаё”аёұаёҮаёҷаёөа№ү 0 B (33) C (17) U 0 A 8 2 аёҲаёІаёҒа№Ғаёңаёҷаё аёІаёһ аёҲаё°а№Җаё«а№ҮаёҷไดпңӢаё§пңҠаёІаёҷаёұаёҒаёҒаёІаёЈа№ҖаёЎаё·аёӯаёҮаё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё”пңӢаёІаёҷаё§аёҙаё—аёўаёІаёЁаёІаёӘаё•аёЈпңҺаёӯаёўпңҠаёІаёҮа№Җаё”аёөаёўаё§ аёЎаёө 50 вҖ“ 33 вҖ“ 17 = 0 аё„аёҷ аё”аёұаёҮаёҷаёұа№үаёҷ аёҷаёұаёҒаёҒаёІаёЈа№ҖаёЎаё·аёӯаёҮаё—аёөа№ҲаёЎаёөаёһаё·а№үаёҷаёҗаёІаёҷаёҒаёІаёЈаёЁаё¶аёҒаё©аёІаё”пңӢаёІаёҷаё§аёҙаё—аёўаёІаёЁаёІаёӘаё•аёЈпңҺаёЎаёө 0 + 8 + 2 = 10 аё„аёҷ 10. аёҷаёұаёҒа№ҖаёЈаёөаёўаёҷаёҒаёҘаёёпңҠаёЎаё«аёҷаё¶а№ҲаёҮаёҲа№ҚаёІаёҷаё§аёҷ 50 аё„аёҷ а№Ғаё•пңҠаёҘаё°аё„аёҷаё•пңӢаёӯаёҮа№ҖаёЈаёөаёўаёҷаё§аёҙаёҠаёІаё„аё“аёҙаё•аёЁаёІаёӘаё•аёЈпңҺаё«аёЈаё·аёӯаё§аёҙаёҠаёІаё аёІаё©аёІаёӯаёұаёҮаёҒаёӨаё© аёӯаёўпңҠаёІаёҮаёҷпңӢаёӯаёў 1 аё§аёҙаёҠаёІ аё–пңӢаёІаёЎаёөаёҷаёұаёҒа№ҖаёЈаёөаёўаёҷа№ҖаёЈаёөаёўаёҷаё§аёҙаёҠаёІаё„аё“аёҙаё•аёЁаёІаёӘаё•аёЈпңҺ 29 аё„аёҷ а№ҒаёҘаё°а№ҖаёЈаёөаёўаёҷаё аёІаё©аёІаёӯаёұаёҮаёҒаёӨаё© 32 аё„аёҷ а№ҒаёҘпңӢаё§аёҲа№ҚаёІаёҷаё§аёҷаёҷаёұаёҒа№ҖаёЈаёөаёўаёҷаё—аёұа№үаёҮаё§аёҙаёҠаёІаё„аё“аёҙаё•аёЁаёІаёӘаё•аёЈпңҺа№ҒаёҘаё°аё аёІаё©аёІаёӯаёұаёҮаёҒаёӨаё©аёЎаёөаёҲа№ҚаёІаёҷаё§аёҷа№Җаё—пңҠаёІаёҒаёұаёҡаёӮпңӢаёӯа№ғаё” 1. 11 аё„аёҷ 2. 13 аё„аёҷ 3. 14 аё„аёҷ 4. 15 аё„аёҷ а№Ғаёҷаё§аё„аёҙаё” а№ғаё«пңӢ A а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаёҷаёұаёҒа№ҖаёЈаёөаёўаёҷаё—аёөа№Ҳа№ҖаёЈаёөаёўаёҷаё§аёҙаёҠаёІаё„аё“аёҙаё•аёЁаёІаёӘаё•аёЈпңҺ вҲҙ n(A) = 29 B а№Ғаё—аёҷ๶ДаёӢаё•аёӮаёӯаёҮаёҷаёұаёҒа№ҖаёЈаёөаёўаёҷаё—аёөа№Ҳа№ҖаёЈаёөаёўаёҷаё§аёҙаёҠаёІаё аёІаё©аёІаёӯаёұаёҮаёҒаёӨаё© вҲҙ n(B) = 32 а№ҖаёЎаё·а№Ҳаёӯ n(A вҲӘ B) = 50 аё„аёҷ аё•пңӢаёӯаёҮаёҒаёІаёЈаё«аёІ n(A вҲ©B) = ? аёҲаёІаёҒ n(A вҲӘ B) = n(A) + n(B) - n(A вҲ©B) а№Ғаё—аёҷаё„пңҠаёІаёҲะไดпңӢ 50 = 29 + 32 - n(A вҲ©B) вҲҙ n(A вҲ©B) = 29 + 32 вҖ“ 50 = 11 аё”аёұаёҮаёҷаёұа№үаёҷ аёҲа№ҚаёІаёҷаё§аёҷаёҷаёұаёҒа№ҖаёЈаёөаёўаёҷаё—аёөа№Ҳа№ҖаёЈаёөаёўаёҷаё—аёұа№үаёҮаё§аёҙаёҠаёІаё„аё“аёҙаё•аёЁаёІаёӘаё•аёЈпңҺа№ҒаёҘаё°аё аёІаё©аёІаёӯаёұаёҮаёҒаёӨаё©аёЎаёөа№Җаё—пңҠаёІаёҒаёұаёҡ 11 аё„аёҷ
- 11. а№ҖаёҒа№ҮаёҮа№Ғаёҷаё§аёӮпңӢаёӯаёӘаёӯаёҡ O-Net а№ҖаёЈаё·а№ҲаёӯаёҮ ๶ДаёӢаё• 1. аёҒа№ҚаёІаё«аёҷаё” A а№ҒаёҘаё° B а№Җаёӣпң’аёҷ๶ДаёӢаё•а№ғаё”а№Ҷ а№ғаёҷа№ҖаёӯаёҒаё аёһаёӘаёұаёЎаёһаёұаё—аёҳпңҺ U а№Җаё”аёөаёўаё§аёҒаёұаёҷ аёӮпңӢаёӯа№ғаё”аё•пңҠаёӯไаёӣаёҷаёөа№үаё–аё№аёҒ 1. аё–пңӢаёІ A вҲ© B = ПҶ а№ҒаёҘпңӢаё§ A = ПҶ а№ҒаёҘаё° B = ПҶ 2. аё–пңӢаёІ A вҲӘ B = ПҶ а№ҒаёҘпңӢวไมпңҠаёҲа№ҚаёІа№Җаёӣпң’аёҷаё—аёөа№Ҳ A = ПҶ а№ҒаёҘаё° B = ПҶ 3. аё–пңӢаёІ A - B = ПҶ а№ҒаёҘпңӢаё§ A = ПҶ а№ҒаёҘаё° B = ПҶ 4. аё–пңӢаёІ A вҲ© B = A вҲӘ B а№ҒаёҘпңӢаё§ A = B аё–пңӢаёІаёӘаёұаёҡ๶ДаёӢаё•аё—аёұа№үаёҮаё«аёЎаё”аёӮаёӯаёҮ๶ДаёӢаё• A аё„аё·аёӯ ПҶ, {1}, {2}, {1, 2}2. а№ҒаёҘаё°аёӘаёұаёҡ๶ДаёӢаё•аё—аёұа№үаёҮаё«аёЎаё”аёӮаёӯаёҮ B аё„аё·аёӯ ПҶ, {2}, {3}, {2, 3} а№ҒаёҘпңӢаё§ A вҲ©B аё„аё·аёӯ๶ДаёӢаё•а№ғаёҷаёӮпңӢаёӯа№ғаё” 1. ПҶ 2. {1} 3. {2} 4. {3} аёҒа№ҚаёІаё«аёҷаё” A а№ҒаёҘаё° B а№Җаёӣпң’аёҷ๶ДаёӢаё•аё—аёөа№ҲаёЎаёөаёҲа№ҚаёІаёҷаё§аёҷаёӘаёЎаёІаёҠаёҙаёҒа№Җаё—пңҠаёІаёҒаёұаёҷ а№Ӯаё”аёў n(AвҲ©B) = 2 а№ҒаёҘаё° n(AвҲӘB) = 103. а№ҒаёҘпңӢаё§аёӮпңӢаёӯа№ғаё”аё•пңҠаёӯไаёӣаёҷаёөа№үа№Җаёӣпң’аёҷаёҲа№ҚаёІаёҷаё§аёҷаёӘаёЎаёІаёҠаёҙаёҒаёӮаёӯаёҮ B вҖ“ A 1. 3 аё•аёұаё§ 2. 4 аё•аёұаё§ 3. 5 аё•аёұаё§ 4. 6 аё•аёұаё§ 4. аёҒа№ҚаёІаё«аёҷаё” A а№ҒаёҘаё° B а№Җаёӣпң’аёҷ๶ДаёӢаё•а№ғаё”а№Ҷ аёһаёҙаёҲаёІаёЈаё“аёІаёӮпңӢаёӯаё„аё§аёІаёЎаё•пңҠаёӯไаёӣаёҷаёөа№ү аёҒ. n(AвҲ©B) = n(A) + n(B) вҖ“ n(A вҲӘ B) аёӮ. n(AвҲӘB) = n(A - B) + n(AвҲ© B) + n(B вҖ“ A) аёӮпңӢаёӯа№ғаё”аё•пңҠаёӯไаёӣаёҷаёөа№үаё–аё№аёҒаё•пңӢаёӯаёҮ 1. аёӮпңӢаёӯ аёҒ. а№ҒаёҘаё° аёӮпңӢаёӯ аёӮ. аё–аё№аёҒ 2. аёӮпңӢаёӯ аёҒ. аёңаёҙаё” а№ҒаёҘаё° аёӮпңӢаёӯ аёӮ. аё–аё№аёҒ 3. аёӮпңӢаёӯ аёҒ. аё–аё№аёҒ а№ҒаёҘаё° аёӮпңӢаёӯ аёӮ. аёңаёҙаё” 4. аёӮпңӢаёӯ аёҒ. а№ҒаёҘаё° аёӮпңӢаёӯ аёӮ. аёңаёҙаё” аёҒа№ҚаёІаё«аёҷаё” A а№ҒаёҘаё° B а№Җаёӣпң’аёҷ๶ДаёӢаё•а№ғаё”а№Ҷ аё–пңӢаёІ n(A вҲӘ B) = 10, n(A - B) = 3 а№ҒаёҘаё° n(B - A) = 55. а№ҒаёҘпңӢаё§ n(A вҲ©B) а№Җаё—пңҠаёІаёҒаёұаёҡаёӮпңӢаёӯа№ғаё”аё•пңҠаёӯไаёӣаёҷаёөа№ү 1. 1 2. 2 3. 3 4. 4
- 12. 6. аёҒа№ҚаёІаё«аёҷаё” A , B а№ҒаёҘаё° C а№Җаёӣпң’аёҷ๶ДаёӢаё•а№ғаё”а№Ҷ а№ғаёҷа№ҖаёӯаёҒаё аёһаёӘаёұаёЎаёһаёұаё—аёҳпңҺ U а№Җаё”аёөаёўаё§аёҒаёұаёҷ а№ҒаёҘаё° n(A) = 50 , n(B) = 40 , n(C) = 30 , n(A вҲ©B) = 15 , n(BвҲ©C) = 13 , n(AвҲ©C) = 17 а№ҒаёҘаё° n(A вҲӘ B вҲӘ C) = 80 аёҲаёҮаё«аёІ n(A вҲ©BвҲ©C) 1. 5 2. 6 3. 7 4. 8 7. аё–пңӢаёІ A , B а№Җаёӣпң’аёҷ๶ДаёӢаё•аёӯаёҷаёұаёҷаё•пңҺа№ҒаёҘаё° C а№Җаёӣпң’аёҷ๶ДаёӢаё•аёҲа№ҚаёІаёҒаёұаё” а№ҒаёҘпңӢว๶ДаёӢаё•а№ғаёҷаёӮпңӢаёӯа№ғаё”аё•пңҠаёӯไаёӣаёҷаёөа№үа№Җаёӣпң’аёҷ๶ДаёӢаё•аёӯаёҷаёұаёҷаё•пңҺ 1. (A вҲ© C) вҲӘ (B вҲ©C) 2. A вҲӘ (BвҲ©C) 3. (C - B) вҲӘ (C - A) 4. (AвҲӘB)вҲ©C а№ғаё«пңӢ A = {ПҶ, 0, 1, {1}} а№ҒаёҘаё° P(A) а№Җаёӣпң’аёҷа№ҖаёһаёІа№Җаё§аёӯаёЈпңҺ๶ДаёӢаё•аёӮаёӯаёҮ A8. B аё„аё·аёӯаё„аёӯаёЎаёһаёҘаёөа№ҖаёЎаёҷаё•пңҺаёӮаёӯаёҮ A а№ҒаёҘаё° C аё„аё·аёӯаё„аёӯаёЎаёһаёҘаёөа№ҖаёЎаёҷаё•пңҺаёӮаёӯаёҮ P(A) аёҲа№ҚаёІаёҷаё§аёҷаёӘаёЎаёІаёҠаёҙаёҒаёӮаёӯаёҮ (B вҲ©C) вҲӘ (BвҲ©C ) а№Җаё—пңҠаёІаёҒаёұаёҡаёӮпңӢаёӯа№ғаё”вҖІ вҖІ 1. 12 2. 14 3. 16 4. 20 9. а№ғаёҷаёӘа№ҚаёІаёҷаёұаёҒаёҮаёІаёҷаёҒаёІаёҠаёІаё”аёӘаёІаёҒаёҘа№Ғаё«пңҠаёҮаё«аёҷаё¶а№ҲаёҮаёЎаёөа№ҖаёҲпңӢаёІаё—аёөа№Ҳ 18 аё„аёҷ а№Ғаё•пңҠаёҘаё°аё„аёҷаёһаё№аё”аё аёІаё©аёІаёЈаёұаёӘа№ҖаёӢаёөаёў аё«аёЈаё·аёӯ аё аёІаё©аёІаёӯаёұаёҮаёҒаёӨаё© аё«аёЈаё·аёӯ аё аёІаё©аёІаёқаёЈаёұа№ҲаёҮа№ҖаёЁаёӘ аёЎаёөа№ҖаёһаёөаёўаёҮаё„аёҷа№Җаё”аёөаёўаё§аё—аёөа№Ҳаёһаё№аё”аё аёІаё©аёІаёЈаёұаёӘа№ҖаёӢаёөаёў аё аёІаё©аёІаёқаёЈаёұа№ҲаёҮа№ҖаёЁаёӘа№ҒаёҘаё°аё аёІаё©аёІаёӯаёұаёҮаёҒаёӨษไดпңӢаё—аёұа№үаёҮаёӘаёІаёЎ аё аёІаё©аёІ аёЎаёө 3 аё„аёҷаёһаё№аё”аё аёІаё©аёІаёқаёЈаёұа№ҲаёҮа№ҖаёЁаёӘа№ҒаёҘаё°аё аёІаё©аёІаёӯаёұаёҮаёҒаёӨษไดпңӢ аёЎаёө 13 аё„аёҷаё—аёөа№Ҳаёһаё№аё”аё аёІаё©аёІаёЈаёұаёӘа№ҖаёӢаёөยไดпңӢ а№ҒаёҘаё°а№ғаёҷ 13 аё„аёҷаёҷаёөа№үаёЎаёө 5 аё„аёҷаё—аёөа№Ҳаёһаё№аё”аё аёІаё©аёІаёӯаёұаёҮаёҒаёӨษไดпңӢ аёЎаёө 9 аё„аёҷаё—аёөа№Ҳаёһаё№аё”аё аёІаё©аёІаёқаёЈаёұа№ҲаёҮа№ҖаёЁаёӘไดпңӢ ไมпңҠаёЎаёөа№ҖаёҲпңӢаёІаё«аёҷпңӢаёІаё—аёөа№Ҳаё„аёҷа№ғаё”аё—аёөа№Ҳ аёһаё№аё”аё аёІаё©аёІаёӯаёұаёҮаёҒаёӨษไดпңӢа№ҖаёһаёөаёўаёҮаё аёІаё©аёІа№Җаё”аёөаёўаё§ аёЎаёөа№ҖаёҲпңӢаёІаё«аёҷпңӢаёІаё—аёөа№ҲаёҒаёөа№Ҳаё„аёҷаё—аёөа№Ҳаёһаё№аё”аё аёІаё©аёІаёқаёЈаёұа№ҲаёҮа№ҖаёЁаёӘไดпңӢа№ҖаёһаёөаёўаёҮаё аёІаё©аёІа№Җаё”аёөаёўаё§ 1. 2 2. 3 3. 4 4. 5 10. а№ғаёҷаёҒаёІаёЈаёӘа№ҚаёІаёЈаё§аёҲаёҷаёұаёҒа№ҖаёЈаёөаёўаёҷаё—аёөа№ҲไดпңӢаёқпңғаёҒаё«аёұаё”аё§пңҠаёІаёўаёҷа№үа№ҚаёІа№Җаёӣпң’аёҷ 3 а№Җаё”аё·аёӯаёҷаёЎаёІа№ҒаёҘпңӢаё§ аёҲа№ҚаёІаёҷаё§аёҷ 40 аё„аёҷ аёһаёҡаё§пңҠаёІаё§пңҠаёІаёўаёҷа№үа№ҚаёІ аё—пңҠаёІаёҒаёҡไดпңӢ 20 аё„аёҷ аё§пңҠаёІаёўаёҷа№үа№ҚаёІаё—пңҠаёІаёңаёөа№ҖаёӘаё·а№үаёӯไดпңӢ 19 аё„аёҷ а№ҒаёҘаё°аё§пңҠายไมпңҠไดпңӢไมпңҠаё§пңҠаёІаё—пңҠаёІаёҒаёҡаё«аёЈаё·аёӯаё—пңҠаёІаёңаёөа№ҖаёӘаё·а№үаёӯ 7 аё„аёҷ аёЎаёөаёҷаёұаёҒа№ҖаёЈаёөаёўаёҷаё—аёұа№үаёҮаё«аёЎаё”аёҒаёөа№Ҳаё„аёҷаё—аёөа№ҲаёӘаёІаёЎаёІаёЈаё–аё§пңҠаёІаёўаёҷа№үа№ҚาไดпңӢаё—аёұа№үаёҮаё—пңҠаёІаёҒаёҡа№ҒаёҘаё°аё—пңҠаёІаёңаёөа№ҖаёӘаё·а№үаёӯ 1. 4 2. 6 3. 8 4. 10
- 13. ๶ДаёүаёҘаёўа№ҖаёҒа№ҮаёҮа№Ғаёҷаё§аёӮпңӢаёӯаёӘаёӯаёҡ O-Net а№ҖаёЈаё·а№ҲаёӯаёҮ ๶ДаёӢаё• 1. аёӮпңӢаёӯ 4 2. аёӮпңӢаёӯ 3 3. аёӮпңӢаёӯ 2 4. аёӮпңӢаёӯ 1 5. аёӮпңӢаёӯ 2 6. аёӮпңӢаёӯ 1 7. аёӮпңӢаёӯ 2 8. аёӮпңӢаёӯ 3 9. аёӮпңӢаёӯ 2 10. аёӮпңӢаёӯ 2 аёһаёҡаёҒаёұаёҡ๶ДаёүаёҘаёўаёҘаё°а№ҖаёӯаёөยดไดпңӢаё—аёөа№ҲвҖҰ MATH HOUSE а№Ӯаё—аёЈ 02-413-2556 -7



![5 аёӘаёЎаёҡаёұаё•аёҙа№ҖаёҒаёөа№Ҳаёўаё§аёҒаёұаёҡ๶ДаёӢаё•аё—аёөа№Ҳаё«пңӢаёІаёЎаёҘаё·аёЎ
(1) аёӘаёЎаёҡаёұаё•аёҙа№ҖаёҒаёөа№Ҳаёўаё§аёҒаёұаёҡаёӘаёұаёҡ๶ДаёӢаё•
AвҠӮB аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ AвҲ©B = A
AвҠӮB аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ AвҲӘB = B
AвҠӮB аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ BвҖІвҠӮAвҖІ
(2) аёӘаёЎаёҡаёұаё•аёҙа№ҖаёҒаёөа№Ҳаёўаё§аёҒаёұаёҡаёҒаёІаёЈаёҒаёЈаё°аё—а№ҚаёІ
AвҲӘB = ПҶ аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ A= ПҶ а№ҒаёҘаё° B= ПҶ
AвҲ©B = ПҶ аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ AвҠӮBвҖІ а№ҒаёҘаё° BвҠӮAвҖІ
AвҖ“ B = ПҶ аёҒа№Үаё•пңҠаёӯа№ҖаёЎаё·а№Ҳаёӯ AвҠӮB
(3) аёӘаёЎаёҡаёұаё•аёҙаёӮаёӯаёҮа№ҖаёһаёІа№Җаё§аёӯаёЈпңҺ๶ДаёӢаё• а№ҖаёЎаё·а№Ҳаёӯ A , B а№Җаёӣпң’аёҷ๶ДаёӢаё•а№ғаё” а№Ҷ
1.) x вҲҲP(A) вҶ” xвҠӮA
2.) ПҶ вҲҲ P(A) а№ҒаёҘаё° AвҲҲ P(A)
3.) ПҶ вҠӮ P(A) , {ПҶ}вҠӮ P(A) а№ҒаёҘаё° {A} вҠӮ P(A)
4.) аё–пңӢา๶ДаёӢаё• A аёЎаёөаёӘаёЎаёІаёҠаёҙаёҒ n аё•аёұаё§ а№ҒаёҘпңӢаё§ P(A) аёЎаёөаёӘаёЎаёІаёҠаёҙаёҒ 2n
аё•аёұаё§
(4) а№ғаё«пңӢ A = {1 , 2 , 3 , вҖҰ , m} а№ҒаёҘаё° B = { 1 , 2 , 3 , вҖҰ , n} а№Ӯаё”аёўаё—аёөа№Ҳ m < n
1.) аё–пңӢаёІ AвҠӮ XвҠӮB аёҲаё°аёЎаёө๶ДаёӢаё• X ไดпңӢ = 2n-m
๶ДаёӢаё•
2.) аё–пңӢаёІ A вҲ© X вү ПҶ а№ҒаёҘаё° X вҠӮB аёҲаё°аёЎаёө๶ДаёӢаё• X ไดпңӢ = 2n
вҖ“ 2n-m
๶ДаёӢаё•
(5) n(A вҖ“ B) = n(A) вҖ“ n(AвҲ©B)
(6) n(AвҲӘB) вҖІ = n(U) вҖ“ n(AвҲӘB)
(7) n[P(A) вҖ“ P(B)] = n[P(A)] вҖ“ n[P(AвҲ©B)]](https://image.slidesharecdn.com/o-net01-151012111355-lva1-app6891/85/O-net-01-MATH-HOUSE-4-320.jpg)

![3. аёҒа№ҚаёІаё«аёҷаё” A = {0, {0}, ПҶ, {ПҶ}, 1} а№ҒаёҘаё° P(A) а№Җаёӣпң’аёҷа№ҖаёһаёІа№Җаё§аёӯаёЈпңҺ๶ДаёӢаё•аёӮаёӯаёҮ A
аёҲа№ҚаёІаёҷаё§аёҷаёӘаёЎаёІаёҠаёҙаёҒаёӮаёӯаёҮ P(A) вҖ“ A а№Җаё—пңҠаёІаёҒаёұаёҡа№Җаё—пңҠаёІа№ғаё”
1. 29 2. 30 3. 31 4. 32
а№Ғаёҷаё§аё„аёҙаё” n(A) = 5Q
аёҲะไดпңӢ n(P(A)) = 25
= 32 вҺҜ 1
а№Ғаё•пңҠ A а№ҒаёҘаё° P(A) аёЎаёөаёӘаёЎаёІаёҠаёҙаёҒаёӢа№үа№ҚаёІаёҒаёұаёҷ 3 аё•аёұаё§аё„аё·аёӯ {0}, ПҶ, {ПҶ}
вҲҙ n(P(A) вҲ© A) = 3 вҺҜ 2
а№Җаёҷаё·а№ҲаёӯаёҮаёҲаёІаёҒ n[P(A) вҖ“ A] = n(P(A)) вҖ“ n(P(A) вҲ© A)
аё”аёұаёҮаёҷаёұа№үаёҷ n[P(A) вҖ“ A] = 32 вҖ“ 3 = 29 аё•аёұаё§
аёҒа№ҚаёІаё«аёҷаё”а№ғаё«пңӢ A а№ҒаёҘаё° B а№Җаёӣпң’аёҷ๶ДаёӢаё•аёҲа№ҚаёІаёҒаёұаё”а№Ӯаё”аёўаё—аёөа№Ҳ n(A вҲӘ B) = 67 а№ҒаёҘаё° n[(A вҖ“ B)вҲӘ(B вҖ“ A)] = 584.
аё–пңӢаёІ n(A) = 32 а№ҒаёҘпңӢаё§ n(B) аёЎаёөаё„пңҠаёІа№Җаё—пңҠаёІаёҒаёұаёҡаёӮпңӢаёӯа№ғаё”аё•пңҠаёӯไаёӣаёҷаёөа№ү
1. 28 2. 35 3. 39 4. 44
а№Ғаёҷаё§аё„аёҙаё” аёҲаёІаёҒа№Ғаёңаёҷаё аёІаёһа№Җаё§аёҷаёҷпңҺ вҖ“ аёӯаёӯаёўа№ҖаёҘаёӯаёЈпңҺ
аёҲаё°аёһаёҡаё§пңҠаёІ n(A вҲӘ B) = n[(A вҖ“ B) вҲӘ (B вҖ“ A)] + n(AвҲ©B)
а№Ғаё—аёҷаё„пңҠаёІаёҲะไดпңӢ 67 = 58 + n(A вҲ©B)
A B
U
A - B B - A
AвҲ©B
вҲҙ n(A вҲ©B) = 67 вҖ“ 58 = 9 вҺҜ вҲ—
а№Җаёҷаё·а№ҲаёӯаёҮаёҲаёІаёҒ n(A вҲӘ B) = n(A) + n(B) - n(A вҲ© B)
аёҲะไดпңӢ 67 = 32 + n(B) вҖ“ 9
аё”аёұаёҮаёҷаёұа№үаёҷ n(B) = 67 вҖ“ 32 + 9 = 44](https://image.slidesharecdn.com/o-net01-151012111355-lva1-app6891/85/O-net-01-MATH-HOUSE-6-320.jpg)






















































