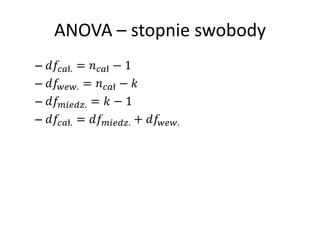Podstawy statystyki dla psycholog¿«w - zaj?cia 13 -ANOVA
- 1. Podstawy statystyki dla psycholog¿«w Jednoczynnikowa ANOVA Zaj?cia 13. Karol Wolski
- 2. ANOVA ¿C po co nam to? ? Czasami chcemy por¿«wna? wi?cej ni? jedna grup?, np. siedem grup poddanych r¿«?nemu leczeniu. Co mo?emy zrobi?? ? Pierwsza my?l, zrobi? test t i por¿«wna? wszystkie 21 mo?liwych par ? Dlaczego nie? Zauwa?my, ?e gdy obierzemy t? strategi?, to b??dy I rodzaju dla wszystkich analiz sumuj? nam si?, a prawdopodobie¿¢stwo odrzucenia prawdziwej hipotezy zerowej ro?nie do ok. 0,66 ¿C = 1 ? (0,95)21 ? I jeszcze jedno nawet je?li wykonamy wszystkie 21 por¿«wna¿¢ to i tak nie mamy obrazu ca?o?ci, mamy jego 21 cz??ci
- 3. ANOVA ¿C wprowadzenie ? Jednoczynnikowa ANOVA pozwala na por¿«wnywanie dw¿«ch lub wi?cej grup jednocze?nie. ? Jest blisko spokrewniona z testem t?. W przypadku por¿«wnania dw¿«ch grup obie techniki daj? to?same oszacowania. Test t mo?na wi?c potraktowa? jako specyficzny przyk?ad ANOVY
- 4. ANOVA ¿C wprowadzenie ? Pomimo tego, ?e m¿«wimy o analizie wariancji technika ta pos?u?y nam do testowania r¿«?nic pomi?dzy ?rednimi ? St?d H0 : = = = ? = ¿C Gdzie k oznacza liczb? warunk¿«w eksperymentalnych/grup ¿C Oczywi?cie hipoteza alternatywna zak?ada, ?e mamy przynajmniej jedn? r¿«?nic?, niezale?nie pomi?dzy, kt¿«ry dwie ?rednimi ¿C Mo?e ona by? jedna, a mo?e by? ich kilka ¿C Nie ma sensu m¿«wi? o hipotezie kierunkowej je?li k>2
- 5. ANOVA ¿C wprowadzenie ? Ca?kowite zr¿«?nicowanie mi?dzy wszystkimi wynikami podzieli? mo?emy na: ¿C Zr¿«?nicowanie wewn?trzgrupowe (inherentne) ¿C jest ono niezale?ne od warunku eksperymentalnego, wynika np. z losowej zmienno?ci pr¿«by ¿C inaczej nazywane b??dem ¿C Zr¿«?nicowanie mi?dzygrupowe ¿C zr¿«?nicowanie ?rednich dla r¿«?nych warunk¿«w eksperymentalnych b?d?ce efektem zr¿«?nicowania inherentnego oraz manipulacji eksperymentalnej
- 6. ANOVA ¿C wprowadzenie ? Logika ANOVA ¿C W skr¿«cie ANOVA polega na dokonaniu dw¿«ch niezale?nych oszacowa¿¢ wariancji populacyjnej oraz por¿«wnaniu ich ze sob? ¿C Pierwsze oszacowanie (wewn?trzgrupowe) oszacowanie tzw. wariancji b??du dokonywane jest na podstawie oszacowa¿¢ wariancji w poszczeg¿«lnych grupach oraz wyci?gni?ciu z nich 2 ?redniej ¿C Drugie (mi?dzygrupowe)
- 7. ANOVA ¿C podzia? sum kwadrat¿«w ? Ka?dy pojedynczy wynik jak otrzymali?my mo?emy zapisa? jako: ¿C X=?rednia generalna + efekt oddzia?ywa¿¢ + zr¿«?nicowanie inherentne ¿C Gdzie: ?rednia generalna to ?rednia ze wszystkich wynik¿«w, oznacza? j? b?dziemy: ¿C Czyli: = + ? + ? ? oznacza ?redni? z grupy, z kt¿«rej pochodzi dany X
- 8. ANOVA ¿C podzia? sum kwadrat¿«w ? Id?c dalej ka?dy wynik mo?emy zapisa? jako jego odchylenie od ?redniej generalnej: ? = ? + ? ? To daje nam ju? mo?liwo?? obliczenia sumy kwadrat¿«w odchyle¿¢ od ?redniej generalnej oraz dla zr¿«?nicowania wew. i mi?dzygrupowego ¿C ?. = ( ? )2 ¿C . = ( ? )2 ¿C . = ( ? )2 ? Gdzie k ¿C liczba grup, - liczba wynik¿«w i-tej grupie, a - ?rednia i-tej grupy
- 9. ANOVA ¿C podzia? sum kwadrat¿«w ? Zatem: ¿C ?. = . + . ¿C Poniewa?: ? = ? + ?
- 10. ANOVA ¿C stopnie swobody ¿C ?. = ? ? 1 ¿C . = ? ? ¿C . = ? 1 ¿C ?. = . + .
- 11. ANOVA ¿C oszacowanie wariancji ? Og¿«lnie wariancj? oszacowa? mo?emy wed?ug 2 wzoru = ? Mamy wi?c: 2 . 2 ? . = - oszacowanie . wariacji wewn?trzgrupowej (b??du) 2 ? . = . 2 + ?¿¢ ¿C . oszacowanie wariacji mi?dzygrupowej
- 12. ANOVA ¿C stosunek F ? Hipoteza zerowa jest utrzymywana je?li stosunek tych dw¿«ch wariancji jest r¿«wny (w granicach b??du losowego) 2 . .?+ ? = 2 = . .? ? Je?li hipoteza zerowa jest prawdziwa to F=1 ? Je?li nie, to stosunek F powinien by? wi?kszy ¿C Sk?d wiadomo o ile wi?kszy? Odnosimy to do rozk?adu F (tak jak wcze?niej do rozk?adu t)
- 13. Rozk?ad F dla r¿«?nych df ? Tablica: http://pl.wikisource.org/wiki/Tablica_rozk%C5 %82adu_F_Snedecora Wikipedia
- 14. Rozk?ad F dla r¿«?nych df ? Rozk?ad jest zawsze prawosko?ny, st?d ca?y obszar odrzucenia znajduje si? po jednej stronie rozk?adu ? Warto?? F nie mo?e by? mniejsza od zera (oszacowania wariancji nie mog? by? bowiem mniejsze ni? zero, w ko¿¢cu s? kwadratami SS) ? Je?li F<1 to zapewne mamy do czynienia z jakim? b??dem pr¿«by
- 15. Za?o?enia ANOVA ? Rozk?ad normalny w populacjach ? Homogeniczno?? wariancji ? Dob¿«r do ka?dej z pr¿«b jest niezale?ny ? Pr¿«by wybierane losowo zgodnie ze schematem losowania zwrotnego.
- 16. ANOVA ¿C wielko?? efektu ? Miara ta nale?y do rodziny r (nazywamy j? eta kwadrat): . ¿C ªÃ2 = ?.
- 17. Co dalej? ? ANOVA odpowiada nam na pytanie, czy gdzie? jest r¿«?nica, pytanie co r¿«?ni si? od czego? ? Mamy do wyboru dwie opcje dalszej analizy ¿C Por¿«wnania post hoc ¿C nie wymagaj? one wcze?niejszych za?o?e¿¢ ¿C Por¿«wnania zaplanowane
- 18. Por¿«wnania post hov ? Aby u?y?, kt¿«rego? z test¿«w pozwalaj?cego dokona? por¿«wna¿¢ post hoc, musimy najpierw otrzyma? istotny stosunek F ? Jednym z takich test¿«w jest test HSD Tukeya ? W przypadk¿«w tych test¿«w, nie nara?amy si? na sumowanie si? b??d¿«w I rodzaju, dlaczego? ¿C Poniewa? nie u?ywamy tutaj rozk?adu, ?rednie istotne stat. to po prostu takie ?rednie, kt¿«re b?d? si? r¿«?ni? o dan? warto?? ¿C R¿«?nice te jednak musz? by? wi?ksze ni? te wymagane przez test t, aby nie nara?a? nas na b??d I rodzaju
- 19. Por¿«wnania zaplanowane ? Planujemy wcze?niej co b?dziemy por¿«wnywa?, nie zawsze interesuj? nas wszystkie por¿«wnania ? Nie jest wymagana istotno?? F ? Aby je wykona? stosujemy test t dla pr¿«b niezale?nych, jednak jako b??d przyjmujemy 2 warto?? . co daje nam dok?adniejsze oszacowanie, a nie obliczamy go tylko na podstawie por¿«wnywanych grup