More Related Content
What's hot (18)
Viewers also liked (7)
Similar to Presentazione Tesi Laurea 2010 (20)
Presentazione Tesi Laurea 2010
- 1. UNIVERSITA DEGLI STUDI DELLINSUBRIAFACOLTADI SCIENZE MM.FF.NN.SCIENZE E TECNOLOGIE DELLINFORMAZIONE MODELLI PER LA DESCRIZIONE DI PROCESSI PROBABILISTICIA cura di: Polidoro Alessio1
- 2. Obiettivo tesi: Entit autonome/agenti/moduli
- 3. Distribuiti
- 4. Comunicazioni di tipo sincrono/asincrono/broadcasting
- 5. Gerarchici
- 6. Probabilistici2Descrizione composizionale di sistemi complessi :
- 7. Automi a stati finitiFSA Controllo di un sistema dinamico sequenziale discreto. Rabin, Scott 1954 Mc Culloch, Pitts 1943Sistema dinamico discreto: S Q : insiemi degli stati q0 : stato iniziale 裡 : alfabeto delle azioni 隆 : 裡 x Q -> Q funzione di transizione F : insieme degli stati finaliNOTA: FSA + DATI Macchina di Turing3
- 8. 4Problema: Estendere la classica teoria degli Automi per modellare/verificare sistemi:Distribuiti
- 9. Temporizzati
- 10. Gerarchici
- 11. ProbabilisticiModelli probabilisticiAutoma probabilistico di Rabin Nel 1963, Michael O. Rabin introduce gli Automi Probabilistici, come generalizzazione di automi non deterministici. Un automa viene descritto attraverso Caratterizzato attraverso una matrice stocastica, definendo per ogni transizione esistente una probabilit, la quale quantifica la possibilit del suo verificarsi. La somma delle probabilit delle transizioni etichettate da un determinato simbolo dellalfabeto uscenti da un determinato stato deve essere necessariamente uguale ad 1: Lo stato iniziale dellautoma probabilistico 竪 dato tramite un vettore coordinata v , le cui componenti rappresentano le probabilit che il sistema si trovi in un determinato stato iniziale, avente valori zero per tutte le componenti tranne una.5
- 12. Modelli per sistemi distribuitiIdea: Un Sistema viene visto come una n-upla di sottosistemi S1, S2 , , Sn interagenti tra loro.
- 13. Ogni componente locale 竪 descritta da un automa a stati finiti.
- 14. Lautoma globale, che descrive lintero sistema, 竪 ottenuto attraverso il prodotto delle componenti locali: gli stati globali raggiungibili sono il prodotto cartesiano degli insiemi degli stati locali ( problema dellesplosione combinatoria degli stati). Le componenti locali, interagendo tra di loro, creano situazioni complesse.6
- 15. Modelli per sistemi distribuitiCriticit: Lapproccio descritto non 竪 composizionale, cio竪 ogni componente di base viene vista come un sistema chiuso, non predisposto alla comunicazione.7
- 16. Modelli per sistemi distribuitiIdea: Necessario adottare un approccio differente , simile a quello per circuiti, consistente nel considerare ogni singola componente come un sistema aperto, in grado di comunicare con altri ai quali 竪 collegato. Un automa verr quindi arricchito da esplicite interfacce di comunicazione . Le componenti di base, aperte alla comunicazione, verranno composte con opportune operazioni (serie, parallelo con e senza comunicazione, feedback), realizzando reti di automi complesse, in modo composizionale. 8
- 17. ObiettivoCalcolare la probabilit di raggiungere o meno stati critici in reti di automi comunicanti attraverso interfacce, che siano: Composizionali (i.e algebra )
- 18. Riconfigurabili
- 19. Gerarchici-> Modelli per sistemi distribuiti e probabilistici9
- 20. Automi con interfacceIdea:Automa < S , T > + insieme di interfacce di comunicazione. Graficamente: Ogni transizione ha un effetto (anche nullo) su ogni interfaccia. Per ogni i, fi: T -> Xi t -> ti (etichettatura) dove ti rappresenta leffetto di t sullinterfacciaXiNota: Z X1 x X2 x Y1 x Y2 x Y3 X x Yleft right10
- 21. Automi con condizioni11Idea: Automi classici + decomposizione dello spazio degli stati in CASI differenti modalit di esecuzione Esempio: FSA Q = { q0 } + F + Qint
- 22. Automi con interfacce e condizioni12Un automa consiste di: Un grafo G = < S , T >.
- 23. Quattro insiemi X, Y, A, B.
- 24. Quattro funzioni : 隆0: T -> X, 隆1: T -> Y (etichettatura di interfacce) 粒0: A -> S, 粒1: B -> S A in-condizioni B out-condizioniLalgebra che descrive automi con interfacce e condizioni 竪 Cospan-Span(Graph)
- 25. Operazioni13 Composizione in serie ( G 属 H ):
- 26. Parallelo senza comunicazione ( G x H ):
- 27. Somma ( G + H ):
- 29. Feedback parallelo:Problema di Monty HallConcludendo 竪 interessante considerare un gioco legato alla teoria della probabilit.Il quale pu嘆 essere applicato al modello Span(Graph) probabilistico, coinvolgendoprobabilit condizionate.Il concorrente inizialmente sceglie tra tre porte disponibili, dietro una si nasconde una macchina, mentre le restanti nascondono una capra ciascuna.Il conduttore dello show, apre una porta mostrando una delle due capre. Successivamente offrir al giocatore la possibilit di cambiare la scelta iniziale. Domanda: Cambiando porta, il concorrente, pu嘆 aumentare le chance di vittoria?14
- 30. SoluzioneLa risposta alla domanda 竪 si. Esistono principalmente tre scenari possibili, con probabilit 1/3 di verificarsi: Il giocatore sceglie la porta dove si nasconde la capra numero 1. Il conduttore, sceglie la porta dove si nasconde laltra capra. Cambiando porta il giocatore vince lauto. Il giocatore sceglie la porta dove si nasconde la capra numero 2. Il conduttore, sceglie la porta dove si nasconde laltra capra. Cambiando porta il giocatore vince lauto. Il giocatore sceglie la porta dove si nasconde lauto. Il conduttore sceglie, una tra le due porte che nascondono una capra. Cambiando il giocatore trova la capra.15
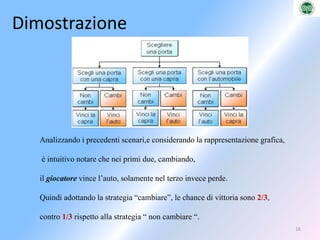
- 31. DimostrazioneAnalizzando i precedenti scenari,e considerando la rappresentazione grafica, 竪 intuitivo notare che nei primi due, cambiando, il giocatore vince lauto, solamente nel terzo invece perde. Quindi adottando la strategia cambiare, le chance di vittoria sono 2/3,contro 1/3 rispetto alla strategia non cambiare .16