disequazioni
- 2. Il concetto di disequazione nella vita di ogni giorno V < 50V < 50 (velocit minore di 50 Km/h) Voto > 60Voto > 60 (promosso!!) 6060
- 3. Il significato dei simboli.Il significato dei simboli. > Maggiore> Maggiore > Maggiore uguale> Maggiore uguale < Minore< Minore < Minore uguale< Minore uguale
- 4. Dati due numeri reali a,b a > b e a < b sono disuguaglianze Una disuguaglianza pu嘆 essere:
- 5. Le disuguaglianze possibili si chiamano disequazioni Sono disequazioni, per esempio: 2x < 6 x + 2 3x + 1 Se al posto della x sostituiamo un numero la disequazione si trasforma in disuguaglianza che pu嘆 essere Vera oppure Falsa Osserva: 2x+1>7 Se al posto della x sostituisco il numero 4 cosa ottengo??? 2(4)+1>7 ovvero 8+1>7 cio竪 9 > 7 竪 una disuguaglianza Vera Allora 4 竪 una soluzione della disequazione..
- 6. Definizione: Risolvere una disequazione vuol dire trovare linsieme dei numeri che sostituiti allincognita la trasformano in una disuguaglianza vera
- 7. Data la disequazione 3x - 1 > 2x + 1 1. Trasporto tutti i termini al primo membro cambiandone il segno 3x - 1 - 2x - 1 >0 2. Riduco i termini simili x - 2 > 0 3. Trasporto dopo il segno maggiore il termine noto (-6) cambiando il segno x > 2
- 8. Data la disequazione 3x - 1 > 2x + 1 Trasporto tutti i termini al primo membro cambiandone il segno: 3x - 1 - 2x - 1 >0 2. Riduco i termini simili x - 2> 0 2. Pongo x-6 uguale ad y ed ottengo y=x-2 Y= x-2 竪 lequazione di una retta la vogliamo disegnare???? Costruiamo la tabella x y -1 -3 0 -2 1 1 2 0 -3 -2 -1 0 1 2 La retta 竪 positiva per x>2 La retta 竪 positiva nella fascia maggiore di 2 cio竪 la soluzione 竪 x>2 + + - - -
- 9. Disequazione: 2(x-3)<x-5 Semplifico lespressione 2x-6<x-5 Porto tutti i termini al primo membro 2x-6-x+5<0 Riduco i termini simili x - 1 < 0 Chiamo y il valore di x-1 y = x-1 Costruisco la tabella per disegnare la retta (x=0; y=-1) (x=1; y=0) Disegno la retta y= x-1 Osservando la retta si vede che risultaOsservando la retta si vede che risulta sotto lasse x (y<0) cio竪 negativa per tutti i valori di x < 1sotto lasse x (y<0) cio竪 negativa per tutti i valori di x < 1 Schema risolutivo ed esercizio guida 1 ++ --
- 10. ax2 + bx + c > 0 ax2 + bx + c < 0 ax2 + bx + c 0 ax2 + bx + c 0 Risoluzione di una disequazione di 2属 grado Le disequazioni di 2 grado si devono ricondurre sempre alla forma:
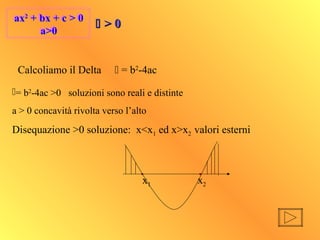
- 11. ax2 + bx + c > 0 a>0 ax2 + bx + c > 0 a>0 Calcoliamo il Delta = b2 -4ac = b2 -4ac >0 soluzioni sono reali e distinte a > 0 concavit rivolta verso lalto Disequazione >0 soluzione: x<x1 ed x>x2 valori esterni x1 x2 > 0> 0
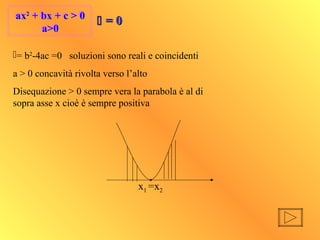
- 12. ax2 + bx + c > 0 a>0 ax2 + bx + c > 0 a>0 x1 =x2 = b2 -4ac =0 soluzioni sono reali e coincidenti a > 0 concavit rivolta verso lalto Disequazione > 0 sempre vera la parabola 竪 al di sopra asse x cio竪 竪 sempre positiva = 0= 0
- 13. ax2 + bx + c > 0 a>0 ax2 + bx + c > 0 a>0 = b2 -4ac < 0 soluzioni complesse coniugate a > 0 concavit rivolta verso lalto Disequazione > 0 sempre vera la parabola 竪 al di sopra asse x cio竪 竪 sempre positiva < 0< 0
- 14. ax2 + bx + c < 0 a>0 ax2 + bx + c < 0 a>0 Calcoliamo il Delta = b2 -4ac = b2 -4ac >0 soluzioni sono reali e distinte a > 0 concavit rivolta verso lalto Disequazione < 0 valori negativi (al di sotto asse x) soluzione: x1 < x < x2 valori interni x1 x2 > 0> 0
- 15. ax2 + bx + c < 0 a>0 ax2 + bx + c < 0 a>0 = b2 -4ac =0 soluzioni sono reali e coincidenti a > 0 concavit rivolta verso lalto Disequazione <0 mai vera la parabola 竪 al di sopra asse x cio竪 竪 sempre positiva x1 =x2 = 0= 0
- 16. ax2 + bx + c < 0 a>0 ax2 + bx + c < 0 a>0 = b2 -4ac < 0 soluzioni sono complesse coniugate a > 0 concavit rivolta verso lalto Disequazione < 0 mai vera la parabola 竪 al di sopra asse x cio竪 竪 sempre positiva < 0< 0
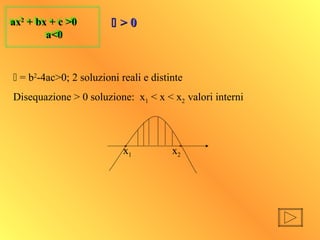
- 17. ax2 + bx + c >0 a<0 ax2 + bx + c >0 a<0 = b2 -4ac>0; 2 soluzioni reali e distinte Disequazione > 0 soluzione: x1 < x < x2 valori interni x1 x2 > 0> 0
- 18. ax2 + bx + c >0 a<0 ax2 + bx + c >0 a<0 = b2 -4ac = 0; 2 soluzioni reali e coincidenti Disequazione > 0 mai vera la parabola 竪 al di sotto asse x x1=x2 = 0= 0
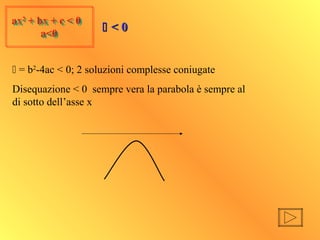
- 19. ax2 + bx + c >0 a<0 ax2 + bx + c >0 a<0 = b2 -4ac < 0; 2 soluzioni complesse coniugate Disequazione > 0 mai vera la parabola si trova al di sotto dellasse delle x quindi 竪 negativa < 0< 0
- 20. ax2 + bx + c < 0 a<0 ax2 + bx + c < 0 a<0 = b2 -4ac>0; 2 soluzioni reali e distinte Disequazione < 0 soluzione: x<x1; x > x2 valori esterni x1 x2 > 0> 0
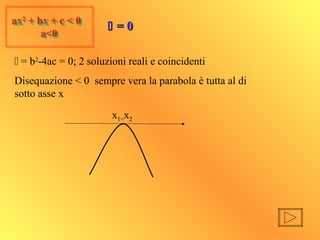
- 21. ax2 + bx + c < 0 a<0 ax2 + bx + c < 0 a<0 = b2 -4ac = 0; 2 soluzioni reali e coincidenti Disequazione < 0 sempre vera la parabola 竪 tutta al di sotto asse x x1=x2 = 0= 0
- 22. ax2 + bx + c < 0 a<0 ax2 + bx + c < 0 a<0 = b2 -4ac < 0; 2 soluzioni complesse coniugate Disequazione < 0 sempre vera la parabola 竪 sempre al di sotto dellasse x < 0< 0
- 23. a>0 ax2 + bx + c > 0 ax2 + bx + c < 0 > 0 due soluzioni reali e disstinte x < x1 e x > x2 Valori esterni x1 < x < x2 Valori interni = 0 Due sol. coincidenti Sempre vera Mai vera < 0 Nessuna soluzione reale Sempre vera Mai vera
- 24. a<0 ax2 + bx + c > 0 ax2 + bx + c < 0 > 0 due soluzioni x1 < x < x2 Valori interni x< x1 e x > x2 Valori esterni = 0 Due sol. coincidenti Mai vera Sempre vera < 0 Nessuna soluzione reale Mai vera Sempre vera
Editor's Notes
- #7: 2x+4&gt;0 2x&gt;-4 x&gt;-2 -5&gt;-2 NOOOO 0,1,2,3,4,5,... 0&gt;-2 1&gt;-2 2&gt;-2