1. RESOLUCION DE LA PRCTICA
VIRTUAL
Grupo 3
Echenique Garcia Brandon Eliel
Fernanadez Villegas Jeanpier
Inga Garcia Julio Esteban
Jaimes Leon erick Roy
Jaimes Plasencia Felipe
Ovalle Quispe Gerson Amadeus
Sanchez Casas Javier
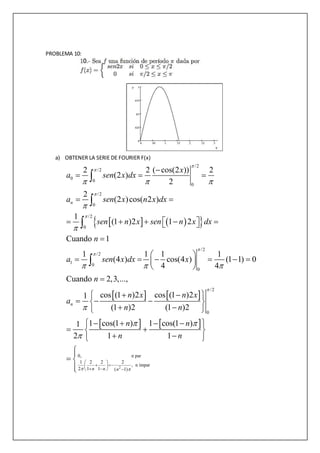
2. PROBLEMA 10:
a) OBTENER LA SERIE DE FOURIER F(x)
/2
/2
0 0
0
/2
0
/2
0
/2
/2
1 0
0
2 2 ( cos(2 )) 2
(2 )
2
2
(2 )cos( 2 )
1
(1 )2 1 2
Cuando 1
1 1 1 1
(4 ) cos(4 ) (1 1) 0
4 4
Cuando 2,3,...,
cos (1 )21
(1
n
n
x
a sen x dx
a sen x n x dx
sen n x sen n x dx
n
a sen x dx x
n
n x
a
緒 刻
緒
2
/2
0
0, n par
1 2 2 2
, n impar
2 1 1 ( 1)
cos (1 )2
)2 (1 )2
1 cos(1 ) 1 cos(1 )1
2 1 1
n n n
n x
n n
n n
n n
緒
種
種
3.
/2
0
/2
0
/2
/2 /2
1 0 0
0
/2
0
Analogamente
2
(2 ) ( 2 )
1
cos (1 )2 cos (1 )2
Cuando 1
1 1 1 (4 ) 1
cos(4 )
2 4 2
Cuando 2,3,...,
(1 )2 (1 )21
(1 )2 (1 )2
1
2
n
n
b sen x sen n x dx
n x n x dx
n
sen x
b dx x dx
n
sen n x sen n x
b
n n
sen
種
(1 ) (1 )
0
1 1
n sen n
n n
逸 種
緒
2
1
De donde,
1 1 2 1 1
( ) (2 ) cos(4 ) cos(8 ) ... .
2 3 15
O tambien,
1 1 2 cos(2 2 )
( ) (2 )
2 4 1n
f x sen x x x
n x
f x sen x
n
4. b) Deducir la convergencia 2
1
1
4 1n n
Considerando el valor X0=0, en la cual f es continua,
se obtiene por convergencia puntual.
2
1
2
1
2
1
1 1 2 cos(2 2 )
(2 ) (0) 1
2 4 1
1 2 1
1
4 1
1 1
2 4 1
n
n
n
n x
sen x f
n
n
n
5. 1
0
0 0
0 2
0
0
0
11. pulso triangular simetr狸co de altura y ancho ajustable es descrito por:
f(x){ } si .
2 (1 cos )
)Muestre que los coeficientes de son: ,
2 ( )
1
x
a
x bb
x
n
t
Un
ab ab nb
a a a
nb
ax
a a dx
b
a a
ｏ
0
0
0
2
0 0 02
2
0
0
0
1
1
1
2
2
b
b
b
b b
ax
dx dx
b
ax
a a dx
b
ax
a ax
b
ab
a ab
b
ab
a
駈
件
醐
0
0 0
0 0
0 0
0 0
0
1
( )cos
1
( )cos 0cos
1
cos cos
1
cos cos
1
cos
1
T
n
b
n
b b
n
b b
n
b b
n
n
ax
a a nxdx
b
ax
a a nxdx nxdx
b
ax
a a nxdx nxdx
b
ax
a a nxdx nxdx
b
ax sennx a sennx
a a nxdx dx
b n b n
asen
a
n
刻
削
削 醐
0 0
2 2
2
cos
(
1
( cos
2 (1 cos )
( )
b b b
n
n
sennx a nx
nx ax
n bn n
asennb sennb a a
a a nb
n n bn bn
ab nb
a
nb
削
削
6. 0 1 2 3 4 5
0
0
2
)Tome 1 y b= calcule y represente las cinco suma parciales
2
como b =0
1
( ) cos cos2 cos3 cos4 cos5
2
Remplezando los valores dados:
2
1
8
2 (1 cos )
( )
(1 cos )
2
(
2
n
n
n
b a
f t a a x a x a x a x a x
ab
a
a
ab nb
a
nb
n
a
n
2
0 1 2 3 4 5
2 2 2 2
)
1
( ) cos cos2 cos3 cos4 cos5
2
1 4 2 4 4
( ) cos cos2 cos3 cos5
8 9 25
f t a a x a x a x a x a x
f t x x x x
7.
2
1
12) Sea la f una funcion dada por f(x) = 1+ ;x 1,1
) ( ).
1
) :
4 1n
x
a Obtener la serie de Fourier de f x
b Deducir la convergencia de la serie
n
0
1
1
1 1
1 1
1
1
, 0
4
an = 1,2,3,4.... an = ( )cos( )
4
1cos( )
1
n = 4 cos( ) cos( )
1 1
4 ( ) cos(
:
T
L
Como f x es una funci坦n par entonces bn y
f t nwt
T
x nwx dx
a x nwx dx nwx dx
an xsen nwx nwx
n n
uego
an
1 1
1 1
1
1
1
0
1
0
1 21
0 0
1
1
) ( )
8
4( )
32
n =
1
(1 )
1
2 (1 )
1
2 (1 )
1 1
2 ( )
1 2
3.
32
( ) 3 + cos( )
n
sen nwx
n
an
n
a
n
ao x dx
T
ao x dx
T
ao x dx
T
ao x x
ao
f t nwt
n
8. Deducirlaconvergencia 2
1
1
4 1n n
Considerandoel valorX0=0,enlacual f escontinua,
se obtiene porconvergenciapuntual.
2
1
2
1
2
1
1 1 2 cos(2 2 )
(2 ) (0) 1
2 4 1
1 2 1
1
4 1
1 1
2 4 1
n
n
n
n x
sen x f
n
n
n
9. 13.-
a)Como f(x) esunafunci坦nimparan=0 ;n=0,1,2,3,..
0
0
1 2
( ) ( )
2 cos( )
n
n
b xsen n dx xsen n dx
x nx
b
n
削
2
; 1,3,5,...
2
; 2,4,6,...
n
n
b n
n
b n
n
Seriaigual a:
1 2
( 1)n
nb
n
Por lotanto:
1
1
( ) 2 3
( ) 2 ( 1) 2 ...
1 2 3
n
n
sen nx senx sen x sen x
f x
n
削
b)Aplicandolaidentidadde Parseval:
2
2 2 2
3 2
2
2
1
2
2
1
1 1 1 1
4 ...
1 2 3
1 1 1
4 4 3 6
1
6
n
n
x dx
x
x dx
n
n
逸
逸
削
C)
2 22 2
0
1
1
( ) 2( )
L
n n
nL
f x dx a a b
L
緒
刻
誌ワ
2
2 1
1
3 1
2
1
3 1
2
1
1 2
2
1
1 2
( 1)
2
1 ( 1)
4
2 3
1 2 ( 1)
4
2 3
( 1)
12
n
n
n
n
n
n
n
n
x dx
n
x
n
n
n
緒
削
ワ
