![22
Integrales de la forma + 賊
2) + =
2
5
3
2 +
5
6
[
5
3
] +
De la forma ; a=
5
3
, v=x, dv=dx
4) =
(+1)
2
4 ( + 1)2 + 2 [
(+1)
2
] +
De la forma 賊 ; a= 2, v= (x+1), dv=dx
6) + =
(モ
1
2
)
2
(
1
2
)
2
+
9
4
+
9
8
ln |(
1
2
) +
( +
1
2
)
2
+
9
4
| +
De la forma 賊 ; a=
3
2
, v=(
1
2
), dv=dx](https://image.slidesharecdn.com/trabajofinalcalculo-140514163212-phpapp02/85/Trabajo-final-calculo-22-320.jpg)
![25
2) 3
3
= (
1
2
2)
3
=
1
2
2 (
1
4
2
2)
=
1
4
1
2
2 (1 2) =
1
8
1
2
2 2
1
8
1
2
2 (2) 2 =
1
16
2 +
1
32
2
2 +
= 2 2 = (2)2
Quinto caso
2) 3
2
=
1
2
[ (3
2
) + (3 +
2
)] =
1
2
5
2
+
1
2
7
2
=
1
2
2
5
5
2
5
2
+
1
2
2
7
7
2
7
2
=
1
5
5
2
1
7
7
2
+
=
5
2
5
2
=
7
2
7
2
4) 4 =
1
2
[( 4) + ( + 4)] =
1
2
(3) +
1
2
5 =
1
2
(
1
3
) (3) 3 +
1
2
1
5
5 5 =
1
6
3 +
1
10
5 +
= (3) 3 = 5 5 aplicando cos(-A)=cosA](https://image.slidesharecdn.com/trabajofinalcalculo-140514163212-phpapp02/85/Trabajo-final-calculo-25-320.jpg)
Trabajo final calculo
- 1. C叩lculo ll Contenido del curso Martin Eduardo Gonzalez Miranda Matricula: 131430 Profesor: Carlos L坦pez Ruvalcaba
- 2. 2 Integrales de Monomios Algebraicos 2. 3 = 3 = 4 4 + 4. 5ヰ = 52 2 + 6. 72 = 73 3 + 8. 54 = 55 5 = 5 + 10. 32 2 = 3 2 2 = 3 2 3 3 = 3 2 + 12. = 2 2 + 14. 43 = 4 3 = 4 4 4 = 4 + 16. モ2 = モ1 1 + = 1 + 18. 4モ2 = 4 モ2 = 4 1 + = 4 +
- 3. 3 20. 4モ3 3 = 4 3 モ3 = 4 3 1 2 = 4 32 + 22. 2 3 2 = 2 3 2 = 4 5 2 5 + 24. 1 2 1 2 = 3 2 3 + 26. 3 ヰ = 3 1 2 = 2 3 2 + 28. 23 2 = 2 3 2 = 3 5 2 10 30. 2 = モ2 = モ1 1 + = 1 + 32. 2 2 = 2モ2 = 2 モ2 = 2 + 34. 3 4 = 3≠4 = 3 ≠4 = 9 3 + 36. 1 2 = ≒ 1 2 = 2 1 2 + 38. 2 3 = 2(3) 1 2 = 12 1 2 +
- 4. 4 40. 3 = 1 3 ≒ 1 2 = 2 3 1 2 + Integrales que conducen a la funci坦n logaritmo natural 1. 2 = 2 = 2 ln|| + = ln|2| + 2. = ln|| + = ln|モ1| + 3. 2 3 = 2 3 = 2 3 ln|| + 4. 3 5 = 3 5 = 3 5 ln|| + 5. = ln|| + = ln| | + 6. 2 3 6 = 4 = 4 ln|| + 7. 2 = 2 = 2 ln|| + 8. 4 = 4 = 4 ln|| +
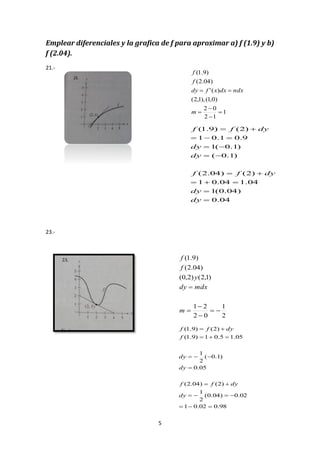
- 5. 5 Emplear diferenciales y la grafica de f para aproximar a) f (1.9) y b) f (2.04). 21.- 23.- 04.0 )04.0(1 04.104.01 )2()04.2( )1.0( )1.0(1 9.01.01 )2()9.1( 緒 緒 dy dy dyff dy dy dyff 1 12 02 )0,1(),1,2( )(' )04.2( )9.1( 緒 m ndxdxxfdy f f 2 1 02 21 )1,2()2,0( )04.2( )9.1( m mdxdy y f f 98.002.01 02.0)04.0( 2 1 )2()04.2( 05.0 )1.0( 2 1 05.15.01)9.1( )2()9.1( 緒 緒 緒 dy dyff dy dy f dyff
- 6. 6 27.-Area. Se encuentra que la medici坦n del lado de un cuadrado es igual a 12 pulgadas, con un posible error de 64 1 de pulgada. Usar diferenciales para aproximar el posible error propagado en el calculo del area del cuadrado. 29.- Area. Se mide el radio del extremo de un tronco y se encuentra que es igual a 14 pulgadas, con un posible error de de pulgada. Utilizar diferenciales para aproximar el posible error propagado en el calculo del area del extremo del tronco. errorindv inindxxdv indx xv 常 緒 3 22 3 75.6 )) 64 1 )(12((33 64 1 errordv ininxdxdv indx 常 緒 375.0 ) 64 1 )(12(22 64 1 errorinininxdxda indx xa 常緒緒 2 2 99.21) 4 1)(14(22 4 1 逸
- 7. 7 31.- Area. La medici坦n del lado de un cuadrado produce un valor igual a 15 cm, con un posible error de 0.05 cm. a) Aproximar el error porcentual en el calculo del area del cuadrado. b) Estimar el m叩ximo error porcentual permisible en la medici坦n del lado si el error en el calculo del area no fue mayor de 2.5% A) %66.0100. 5.2 5.1 _ _15)05.0)(15(22 05.0 2 緒 常緒緒 porcentualError areaerrorininxdxdx indx xa B) M叩ximo error porcentual de lado= 1.25% %25.1187.0 %10015 1875.0 30 625.5 _ 625.5)_)(15(2 625.5) 100 %5.2 (25.2 100. 25.2 %5.2 緒 緒 ladoerror ladoerror error error
- 8. 8 Integral de la potencia de una suma 2) (7x2 1)3/2 x dx = 1/2 (7x2 1)3/2 x dx= (1/2)(1/14) (7x2 1)3 x dx=1/28 * (7x2 1)4/4 = 1/112 *(7x2 1)4 + c 4) x (2+x2) dx = 遜 * (2 + x2)2 /2 = 村 (2 + x2)2 + c 6) (x3 + 2)3 x2 dx = 1/3 * (x3 + 2)3 x2 dx = 1/3 * (x3 + 2)4 /4 = 1/12 * (x3 + 2)4 +c 8) - (4-x)3 2 dx= 2 -(4-x)3 dx = 2 * (4-x)4/4 = 遜 (4-x)4 + c 10) u du = u * (3- 2u2)1/2 du = -1/4 u * (3- 2u2)1/2 du = -1/4 * (3-2u2)3/2 / 3/2 = -1/6 (3 22)3 + c 12) 3x dx/ (x2 + 3)2 = 3x dx * (x2 + 3)-2 = 3/2 x dx * (x2 + 3)-2 = 3/2 * (x2 + 3)-1/-1 =-3/2 * 1/(x2 + 3) + c 14) 2x2 dx / + = 2x2 dx * (a + bx3)-1/2 = 2/3b * (a + bx3)1/2/ 遜 = 4/3b * + 3 + c 16) dv / = dv * (1-v/2)-1/2 = -2 dv * (1-v/2)-1/2 = -2 * (1- v/2)1/2/ 遜 = -4 * 1 2 + c
- 9. 9 18) x2 + 4x 10 dx / (x + 2)2 = x2 +4x -10 dx * (x+2)-2 = x + 14/(x+2) + c 20) dx = (x4-x2)1/2 dx = (2 1)3 / 3 + c Casos especiales 2) (4x2-1) 5x dx = 5/8 (4x2-1)2 / 2 = 5/16 (4x2-1)2 + c
- 10. 10 Integrales de las funciones exponenciales 2) 8x/2 * 遜 dx = (8x/2 / ln8) + c 4) -3a5x * 5 dx = (-3a5x / lna) + c 6) bax^2 x dx = 遜 *(bax^2 / lna) +c 8) 10x^2 + 1 x dx = 遜 * (10x^2 + 1 / ln10) + c 10) dx / 74x = -村 * 7-4x / ln7 = (-1 / (4*74x * ln7)) + c 12) 5e2t dt = 遜 * 5e2t / lne = (5e2t / 2) + c 14) 5eay dy = 1/a * 5eay / lne = (5eay / a) + c 16) / dx = * x-1/2 dx = 2 + c 18) dx = ex^1/2 dx = 2 * + c 20) ( * ) dx / = (2 *( 2) ) / (ln2 + lne) + c 22) (e2x + 3)2 dx = e4x^2 + 6e2x + 9 dx = 村 e4x + 3e2x + 9x + c
- 11. 11 24) (e(x/2) + 4) dx / ex = e(x/2) dx / ex + 4 dx / ex = (-2 / ) (4 / ) + c
- 12. 12 Integrales en que intervienen la tangente, cotangente, secante y cosecante 2) tg x3 x2dx= 1/3 ln |sec x3| +c 4) 3 ctg 2x dx = 3/2 ln |sen 2x| + c 6) ctg dx / = 2 ln |sen | + c 8) sec (x2 /3) x dx = 3/2 ln |sec(x2/3) + tg (x2/3)| + c 10) ax sec ax dx = 1/ lna * ln |sec(ax) + tg(ax)| +c 12) -2 csc (3-2x) dx = ln |csc(3-2x) - ctg(3-2x)| + c 14) sec (x/2) tg (x/2) dx =sec (x/2) dx - tg(x/2) dx = 2 ln |sec(x/2) + tg(x/2)| - 2 ln |sec(x/2)| + c 2) sen 2x dx / (3 + cos 2x) = -1/2 sen 2x dx / (3 + cos 2x) = -1/2 ln |3 + cos 2x|+ c 4) csc2 u du / (3-ctg u) = ln |3-ctg u| + c 2) b dt / ctg(a bt) = - tg(a- bt) b dt = -ln |sec(a bt)| + c
- 13. 13 4) a dx / ( ) = 2a csc a dx = 2a ln |csc ctg | + c 6) xex^2 dx/ ctg ex^2 = 遜 tg ex^2 xex^2 dx = 遜 ln |sec ex^2| + c
- 14. 14 Integrales que conducen a las funciones trigonom辿tricas 2) cos (x/2) dx = 2cos(x/2) dx = 2 sen(x/2) + c 4) cos (1- x2) x dx = -1/2cos (1-x2) x dx = -1/2 sen (1-x2) +c 6 2/3 sen (a x/2) dx = (2/3)*(-2) sen (a x/2) dx =4/3 cos (a- x/2) +c 8) csc2 (1- ) dx / = 2 csc2 (1- ) dx / = 2 ctg (1 - ) + c 10) sec e-x tg e-x e-x dx = -Sec e-x + c Caso especial 2) 2 dx / 1 cos 2x =2 (dx/ (1-cos 2x)) * ((1+cos 2x) /(1+cos2x)) dx = 2 (1/2) (1 + cos 2x)/(1-cosx)2 = (1+ cos 2x)/ sen22x = csc22x + ctg 2x * csc 2x = -ctg 2x csc 2x + c 4) 5 dx / (1 sen 2x) = 5 dx / (1- sen2x) = 5(1/2) ( 1+sen2x/(cos22x) ) =5/2 sec22x dx + 5/2 tg2x * sec 2x dx = 5/2 tg 2x + 5/2 sec2x + c
- 15. 15
- 16. 16 Integrales de las formas , + , 54 2 2 4 2 x dx 42 7 xa xdx c ax arcsen x 72 1 2 2 )3(4 3 x dx 222 32 3 34 3 x dx x dx c x arcsen 2 3 2 1 3 Casos Especiales: Caso 1.- 222 12 3 423 3 x dx xx dx c x arcsen 2 1 3 54 4 2 x dx 22 1 ua bdu 42 7 xa xdx 2 23 v dv 19 2 yy dy x x e dxe 2 1 6.- 4.- 2.- 8.- 10.- 12.- 緒 c y arc yy dy 1 3 sec 1 1 13 3 1 3 22 cyarc 3sec 23 2 xx dx 2.- 駕 22 2 2 3 4 1 4 1 2 32 4 9 4 9 3 x dx x dx xx dx 緒 c x arcsen x dx 2 1 2 3 2 3 2 1 22 cxarcsen 32 2 23 3 xx dx 4.- 2 45 3 tt dx 6.- c x arctg 5 2 5 2 22 1 au du b 緒 c au arctg a b 1 cauarctg a b )( v dv 23 2 2 1 c v arcsen 3 2 2 1 carcsenex 14.- 222 23 3 8845 3 45 3 tt dx tt dx tt dx c t arcsen 3 2 3
- 17. 17 Caso 2.- Caso 3.- 8.- 10.- 12.- 2 352 xx dx 52xx dx 544 2 xx dx dx x x 2 9 23 dx x x 2 161 35 dx x x 254 2 2 2.- 4.- 6.- 駕 4 5 34 9 5412 95412128 2 2 2 1 2 xx dx xx dx dxxxx 駕 222 5623 1 11513 1 11513 x dx xx dx xx dx c x arcsen 7 56 3 1 222 215112 x dx xx dx c x arctg 2 1 2 1 212 4 4 1 52244 22 x dx xx dx c x arctg 2 12 4 1 駕 駕 2 2 1 2 22 9 392 99 3 2 x dx dxxx x dx x xdx c x arcsenx 3 293 2 駕 2 2 1 2 22 161 5161 4 3 161161 5 3 x dx dxxx x dx x xdx cxarcsenx 4 4 3 161 16 5 2 c x arctgx 5 2 5 1 254ln 8 1 2 駕駕駕 2548 1 525 1 254254 22222 x xdx x dx x xdx x dx
- 18. 18 駕駕 723 32 51212129 32 5129 32 222 x dxx xx dxx xx dxx dx xx x 5412 38 2 駕 2 2 2 2 2 3 1 2 9 1 2 32 9 4 5 4 9 4 9 3 2 9 x dx x dx xx dx cxarcsen xx 2 3 2 9 2 1 5412 2 1 2 2.- dx xx x 5129 32 2 dx xx x 2 3 54 4.- 6.- c a v arctg a av aav dv av vdv av dvv 3 )ln( 1 3 3 22 222222 cxarctgxx 235129ln 9 1 2 c a v arcsenva va dv dvvva va dv va vdv va dvv x dxx xx dxx 駕駕駕 4 42 2 1 4 4 323 54 333 54 22 22 2 1 22 222222 22 c x arcsenxx 3 32 34 2
- 19. 19 Integrales de las formas , 2) x dx / 4x4 1 = 1/2 * x dx / 4x4 1=resultado 1/43 ln |(2 3)/(2 + 3)| + c 4) 2x dx / (25-36x2) = 1/6 * 2x dx / (25-36x2) = (1/6)*(1/10) ln|(5+6x2)/(5-6x2) = resultado 1/60 * ln|5+6x2 / 5-6x2 | +c 6) dx/3-2x2 = 1/2 * dx/3-2x2 =resultado 6/ 12 ln |(3 - 2 )/ (3 + 2 )| + c 8) 2 2 2 2 1 1 6 ln 2 5 (x 2 1) 5 1 ( 1) ( 6) 2( 6 1 6 ln 12 6 1 66) 1 6 1 dx dx dx x x x x x x a v x dv d x C x x 10) du / (9-6u-3u2) = - du/(3u2 + 6u-9) = du/-(3u2-6u+9) -9 +9 =- du/(3u-3)*(u+3) = resultado= 1/12 ln| (3+u)/(1-u)| + c 12 (2-3z) dz/ 9-16z2 = 村 *2 dz/ (9-16z2) 村 *3z dz /(9-16z2) = resultado = 1/12 ln| (3+4z)/(3-4z)| + c
- 20. 20 14) 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ( 3) ( 3) (x 3) 3 4 5 (x 4 4) 5 4 ( 2) 9 2 2 ( 2) 1 int 1 #1 ln 4 5 4 5 2 4 5 2 4 1 int#2 3 3 (3)( 2 2 2 ( 2) (3 5 ) 2(3 x x dx vdv dv dx dx dv x x x x v a v a v a v x x v vdv x dx x x v a x x v x x dv x dv dx v a x v 2 2 3 1 1 )ln ln 1 1 1 ln 4 5 ln 2 2 5 ) 2 3 2 5 3 2 x x C x x a v x x dv dx resu xl o Ct xd x a
- 21. 21 Integrales de la forma + 2) 2+2+5 = (+1)2+4 = | + 1 + ( + 1)2 + 22| + = | + 1 + (2 + 2 + 5)| + V=x+1 a=2 = 4) (2y1)dy 2y2+4y+10 = (2y1)dy 2(y2+2y+5) = 1 2 (2y1)dy (y2+2y+1+4) = 1 2 (2y1)dy (y+1)2+22) = 1 2 (2y1)dy (y+1)2+22) = 1 2 ((tan慮1)1)2sec慮2d慮 2sec慮 = 1 2 (4tan慮 3)sec慮d慮 = 4 2 (tan慮)sec慮d慮 3 2 sec慮d慮 = 4 2 sec慮 3 2 ln|sec慮 + tan慮| + c = 22(y2+2y+5) 2 32 2 ln | (y2+2y+5) 2 + y+1 2 | + c = +1 (+1)2+22 = 2 (+1)2+22 ＄ = +1 2 ( + 1)2 + 22 = 2 22 = 6) (2+1) 325 = (2+1) 325 2 = 2ヰ 325 2 + 325 2 = 1 3 32 5 + 1 3 |3 + 32 5| +
- 22. 22 Integrales de la forma + 賊 2) + = 2 5 3 2 + 5 6 [ 5 3 ] + De la forma ; a= 5 3 , v=x, dv=dx 4) = (+1) 2 4 ( + 1)2 + 2 [ (+1) 2 ] + De la forma 賊 ; a= 2, v= (x+1), dv=dx 6) + = (モ 1 2 ) 2 ( 1 2 ) 2 + 9 4 + 9 8 ln |( 1 2 ) + ( + 1 2 ) 2 + 9 4 | + De la forma 賊 ; a= 3 2 , v=( 1 2 ), dv=dx
- 23. 23 Integral de las potencias del seno y/o coseno. Primer caso. 2) 1 2 3 4 4 = 1 2 3 4 4 = 1 2 1 4 3 4 cos 4 4= 1 32 4 4 + = 4 4 4) 5 5 3 5 3 4 = 4 5 5 3 5 3 = 4 3 5 5 5 3 5 3 5 3 = ( 12 5 ) ( 1 6 ) 6 5 3 = 2 5 6 5 3 + = 5 3 5 3 6) 1 3 2 2 2 = 1 3 2 2 2 = 2 1 3 2 2 ( 2 ) 1 2 = ( 2 3 ) ( 1 3 ) 3 2 = 2 9 3 2 + = 2 1 2 8) (2 ) (2 ) = 1 2 2(2 ) + = (2 ) 1 = (2 ) 10)(2 tg 3 + 2 5 2ヰ2) = 2 ＄3 + 2 5 2ヰ2 = 2 3 ＄3 3 + 1 5 2 5 5 1 2 2ヰ2 2 = 2 3 ln|3| + 1 5 ＄5 1 4 2 2 + = 3 = 5 = 2 2 Segundo caso 2) 3 2 = 2 2 2 = (1 2 2 ) 2 = 2 2 2 2 = 2 2 1 2 2 2 2 ( 2 ) 1 2 = 2 2 + 2 3 3 2 + = 1 2 = 2 1 2
- 24. 24 4) 3 5 = 2 5 5 = (1 2 5)5 = 5 2 5ヰ5 = 1 5 5 5 1 5 2 5 5 5 = 1 5 5 1 15 3 5 + = 5 = 5 5 6) 2 ヰ3 = 2 (1 2 ) = 2 4 = 1 3 3 1 5 5 + 8) 3 3 5 3 = 2 3 3ヰ5 3 = (1 2 3) 5 3 3 = 1 3 5 3 (3)3 1 3 7 3 (3)3 = 1 18 6 3 + 1 24 8 3 + = 3 3 = 3 3 Tercer caso 2) 2 = 1 2 + 1 2 2 = 1 2 + 1 2 1 2 2 2 = 1 2 + 1 4 2 + = 2 2 4) 4 = ( 1 2 1 2 2) 2 = ( 1 4 2 1 2 1 2 2 + 1 4 2 2) = 1 4 1 2 2 + 1 4 2 2 = 1 4 ( 1 2 ) ( 1 2 ) 2 2 + ( 1 8 + 1 8 4) = 1 4 ( 1 2 ) ( 1 2 ) 2 2 + 1 8 + ( 1 8 ) 1 4 4 4 = 3 8 1 4 2 + 1 32 4 + = 2 2 = 4 4 Cuarto caso
- 25. 25 2) 3 3 = ( 1 2 2) 3 = 1 2 2 ( 1 4 2 2) = 1 4 1 2 2 (1 2) = 1 8 1 2 2 2 1 8 1 2 2 (2) 2 = 1 16 2 + 1 32 2 2 + = 2 2 = (2)2 Quinto caso 2) 3 2 = 1 2 [ (3 2 ) + (3 + 2 )] = 1 2 5 2 + 1 2 7 2 = 1 2 2 5 5 2 5 2 + 1 2 2 7 7 2 7 2 = 1 5 5 2 1 7 7 2 + = 5 2 5 2 = 7 2 7 2 4) 4 = 1 2 [( 4) + ( + 4)] = 1 2 (3) + 1 2 5 = 1 2 ( 1 3 ) (3) 3 + 1 2 1 5 5 5 = 1 6 3 + 1 10 5 + = (3) 3 = 5 5 aplicando cos(-A)=cosA
- 26. 26 Integrales de las potencias de la tangente y cotangente 4＄ヰ2 ヰ = 4 ＄2 2 = + ｐ = 2 ＄ ヰ2 = 2 ＄ ヰ2 揃 () 1 2 = 22 2 = + ｐ = 1 2 () 1 2 ＄2 2 2 2 = 1 2 ＄2 2 2 = + ｐ = 2 2 2 ＄3 2ヰ = ＄2(＄2 2) = ＄2(2 2 1) = ＄2ヰ2 2ヰ- ＄2ヰ = ヰ|| + ＄5 3ヰ = ＄3 3(＄2 3) = ＄3 3(2 3 1) = ＄3 3ヰ2 3ヰ ＄3 3ヰ ＄3 3ヰ = ＄3(2 3 1) = ＄3ヰ2 3 + ＄3= + ヰ|| +
- 27. 27 ＄6 ヰ = ＄4 (＄2 ) = ＄4 (2 1) = ＄4 2 ヰ ＄2 (2 1) = ＄2 ヰ2 ヰ + ＄2 ヰ = + + (＄ + 3) = ＄ + 2＄3 + 9 = + || + +
- 28. 28 Sustituci坦n trigonometrica 1.- 2 49 xx dx 8.- 10.- dx x x 6 2 3 2 16 駕 緒緒緒 c ctg dctg sen d x x 5 5 16 1 csc 16 1 4 cos16 24 62 4 6 3 2 縁縁 縁 駕 緒緒緒 縁縁 縁縁 dd sen dctg xx dx csc 3 1cos cos 1 3 1 sec 3 1 )2(3 22 cctg |csc|ln 3 1 縁 dxdxtg x tg x x x x sen 緒緒 緒 縁縁縁 2 2 2 2 sec 2 3 2 3 3 2 cos 3 49 49 3 cos 49 2 c x x | 2 349 |ln 3 1 2 722 xx dx 駕 緒 csend xx dx 縁縁 7 1 cos 7 1 )7( 222 77 7 )7( sec7 cos 77 cos )7( 2 222 222 緒 緒緒 xtg xx tg x x x xx sen 縁 c x x 7 7 1 2 c x x 5 22 4 18 1 22 22 22 4 4cos4 4 4 cos 4 4 x x tg x x xsen x sen 緒 緒 縁 縁
- 29. 29 Integraci坦n por partes 1.- dx x xcoc 2 緒緒 駕 dxdx x sen x xsendx x sen x xsen 2 1 2 )2)(2( 2 2 2 2 2 2 4.- xdxln 緒 dx x xxx 1 ln 6.- 緒 xdxx ln2 駕 緒 dxx x x x dx xx x 2ln1ln 1.- xdxx cos2 駕 xsenxdxsenxx 22 駕 xdxxxsenxx coscos22 c xx xsen 2 cos4 2 2 2 2 2 cos x senv dx x dv xu dxdu c xx x 1ln 1 2 ln 1 xv dxxdv xu dx x du cxxx ln xv dxdv xu dx x du ln 1 senxv xdxdv xu xdxdu cos 2 2 xv senxdxdv xu dxdu cos csenxxxsenxx 2cos22
- 30. 30 4.- dxex x22 駕 dxxeex xx 222 2 1 緒 dxexeex xxx 2222 2 1 2 1 2 1 1.- arctgxdx dx x x xarctgx 2 1 2 2 1 5.- dxxArcSenx2 駕 dxxxarcsenx x dx x x x arcsenx x 4)1( 221 2 2 2 1 432 22 4 2 2 6.- xdxSenxSen3 x x ev dxedv xu xdxdu 2 2 2 2 1 2 x x ev dxedv xu dxdu 2 2 2 1 cexeex xxx 2222 4 1 2 1 2 1 cxarcsenx x 2 1 42 2 1 2 1 2 2 41 2 2 2 2 x v xdxdv arcsenxu dx x du 緒 xdxxxxsen 3coscos3cos3 緒 dxxxxxsen 4cos)2cos( 2 1 3cos3 cxsenxsenxxsen 4 8 3 2 4 3 cos3 xv senxdxdv xsenu xdxdu cos 3 3cos3 xv dxdv arctgxu dx x du 2 1 1 cxxarctgx |1|ln 2 1 2
- 31. 31 Integraci坦n por sustituci坦n algebraica 2.- xdxx 9 緒緒緒 c mm dmmmmdmmm 3 18 5 29229 35 242 3.- dx x x 1 駕 ds s s ssds s s ) 1 (22 1 22 css arctan2)(2 4.- 1x e dx 緒 緒 cp p dp dp pp p p dp p p arctan2 1 2 1 2 2 22 2 7.- x dx 9 cp p dpp p dppp 緒 駕 36 3 4 94 )9(4 3 2 2 cex 1arctan2 1 2 |1|ln 1 1 2 2 2 緒 p p dx px ep ep x x mdmdx mx mx xm 2 9 9 9 2 2 緒 cxx 35 969 5 2 cx 93639 3 4 3 dpppdx px xp xp xp )9(4 )9( 9 9 9 2 22 2 2 緒 cxx arctan22 sdsdx sx xs 2 2
- 32. 32 Integraci坦n por fracciones parciales CASO 1 1.- 42 x dx 5.- dz zzz z 2 63 23 2 dz zzz z )2( 63 2 2 )2()1()1)(2(卒63 12)1)(2( 63 )1)(2( 2 2 緒 zczzbzzzaz z c z b z a zzz z zzz si z=-2 si z=1 si z=0 221 )2)(2( 22 1 2222 1 xbxa xx x b x a x b x a xx cxxdx x b dx x a xx dx |2|ln 4 1 |2|ln 4 1 22)2)(2( c x x | 2 2 |ln 4 1 駕 12)1)(2( 63 2 z dz c z dz b z dz adz zzz z czzz czzza |1|ln3|2|ln3||ln3 |1|ln3|2|ln3||ln c z zz | )1)(2( |ln3 3 618 b b 3 39 c c 3 26 a a
- 33. 33 CASO 2.- 駕駕駕 dx x c dx x b dx x a dx xx xx dx xxx xx 22 2 2 2 )1(1)1( 18 12 18 )()1()1(18 )1(1)1( 18 22 22 2 xcxbxxaxx x c x b x a xx xx 緒 Si x=0 si x=-1 si x=1 6 6 緒 c c 4.- du uu u 23 4 2 8 2)2( 8 22 4 u c u b u a du uu u 22 )2()2(8 cuubuauau 緒 Si x=-2 si x=0 si x=1 c x x 1 6 ||ln c x cxbxa | 1 )1( |ln|1|ln||ln 1 a1 0 62410 2410 b b cba 2 84 42 82 2 82 2 23 3 34 423 u u uu u au uuu 駕 駕 件 э du u c du u b du u a du du uu u udu uu u 2 2 2 84 2 2 8 2 23 2 23 4 2 48 c c 2 21234 緒 a a 4 28 緒 b b cu u a uu u |2|ln2||ln22 2 2
- 34. 34 Integraci坦n por fracciones parciales 1.- dx xx x 41 22 2 Si x=0 si x= i si x2= -4 6.- dx x xxx 22 23 )1( 222 )()1)((222 223 dcxxbaxxxx 緒 Si x= 0 x= i si= 1 22222 22 )2(411 2 2 41 x dx d x xdx c x dx b x xdxa dx x dx dx x bax c x arctg d x c arctgxbx a 22 |4|ln 21 1 ||ln 2 22 )1)(()4)(( 41)4)(1( 222 2222 2 xdcxxbaxx x dcx x bax xx x 3 4 0 364 )3(24 2 14)1(44 緒 緒 緒緒 d c dci dci ix x 0 03 3 1 0 3310 緒 a a b a baii db 40 c x arctgxarctgxx 23 4 |4|ln 3 1 ||ln 22 22222 222 )1()1(11 2 2 )1(1 x dx ddx x x c x dx b x xdxa x dcx dx x bax 2 2 b db 0 1 222 緒 d c dcii dciii 1 01)4(227 a a c x arctgxx 1 1 2 1 2|1|ln 2 1 2 2 c x arctgxx )1(2 1 2|1|ln 2 1 2 2