Ringkasan Materi Turunan Parsial Matematika
0 likes19 views
Dokumen ini membahas turunan parsial dari fungsi dua variabel, yaitu z = f(x,y), yang menunjukkan cara menghitung turunan parsial terhadap x dan y dengan beberapa notasi dan contoh. Selain itu, ada penjelasan tentang diferensial total dan aturan rantai dalam konteks fungsi yang terdefinisikan melalui variabel lain. Terdapat juga latihan untuk menentukan turunan parsial dari beberapa fungsi yang diberikan.
1 of 12
Download to read offline


![ŌĆó Turunan parsial z = f(x,y) terhdp y ditulis
didefinisikan sbb.
Contoh:
)
,
(
)
,
( y
x
f
y
x
f
y
z
y
y
’ĆĮ
’éČ
’éČ
’ĆĮ
’éČ
’éČ
’āĘ
’āĖ
’āČ
’ā¦
’ā©
’ā” ’ĆŁ
’Ć½
’ĆĮ
’ĆĮ
’éČ
’éČ
’é« k
y
x
f
k
y
x
f
y
x
f
y
x
f
y k
y
)
,
(
)
,
(
lim
)
,
(
)
,
(
0
’Ć© ’Ć® .
2
2
lim
2
lim
]
[
]
)
[(
lim
)
,
(
)
,
(
lim
)
,
(
x
:
Lengkapnya
.
2
maka
)
,
(
0
2
0
2
2
2
2
0
0
2
2
x
h
x
h
h
xh
h
y
x
y
h
x
h
y
x
g
y
h
x
g
y
x
g
x
z
x
y
x
y
x
g
z
h
h
h
h
’ĆĮ
’Ć½
’ĆĮ
’āĘ
’āĘ
’āĖ
’āČ
’ā¦
’ā¦
’ā©
’ā” ’Ć½
’ĆĮ
’āĘ
’āĘ
’āĖ
’āČ
’ā¦
’ā¦
’ā©
’ā” ’Ć½
’ĆŁ
’Ć½
’Ć½
’ĆĮ
’āĘ
’āĖ
’āČ
’ā¦
’ā©
’ā” ’ĆŁ
’Ć½
’ĆĮ
’éČ
’éČ
’ĆĮ
’éČ
’éČ
’Ć½
’ĆĮ
’ĆĮ
’é«
’é«
’é«
’é«](https://image.slidesharecdn.com/turunanparsial-240724235352-d3e4ea74/85/Ringkasan-Materi-Turunan-Parsial-Matematika-3-320.jpg)





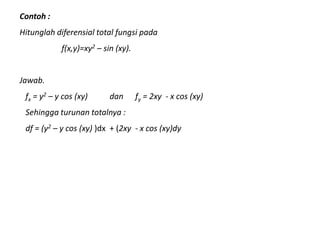


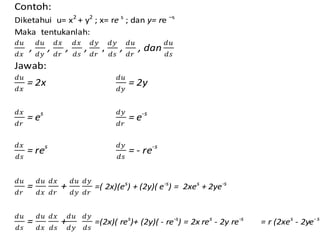
Ad
Recommended
Pertemuan 3 turunan dan aturan rantai
Pertemuan 3 turunan dan aturan rantaiSenat Mahasiswa STIS
╠²
Dokumen ini membahas tentang turunan parsial dan aturan rantai untuk fungsi multivariat, mencakup cara menentukan turunan parsial terhadap variabel independen x dan y, serta menjelaskan konsep turunan parsial tingkat dua dan tiga. Contoh penerapan pada fungsi-fungsi tertentu disertakan untuk memudahkan pemahaman. Selain itu, terdapat penjelasan mengenai aturan rantai untuk fungsi dua dan tiga variabel serta fungsi dengan n variabel.Turuna parsial fungsi dua peubah atau lebih
Turuna parsial fungsi dua peubah atau lebihMono Manullang
╠²
Dokumen ini menjelaskan konsep turunan parsial untuk fungsi dua dan tiga peubah, termasuk bentuk eksplisit dan implisit. Diterangkan juga metode untuk menghitung turunan parsial, serta memberikan contoh dan rumus-rumus yang relevan. Di dalamnya, terdapat pembahasan mengenai diferensial total dan cara menentukan turunan parsial dari fungsi-fungsi baik dalam bentuk eksplisit maupun implisit.Diferensial parsial
Diferensial parsialyenisaja
╠²
Dokumen ini membahas tentang persamaan diferensial parsial dan aplikasinya dalam fisika, termasuk contoh penyelesaian turunan parsial serta konsep-proses dalam termodinamika dan gelombang. Terdapat penjelasan tentang metode diferensial total, aturan rantai, dan hubungan Maxwell dalam konteks termodinamika. Sebagai tambahan, pengantar mengenai kalkulus dan perhitungan volume pada fenomena fisik juga disampaikan.Persamaan differensial parsial
Persamaan differensial parsialMoch Harahap
╠²
Makalah ini membahas tentang persamaan diferensial parsial, yang merupakan persamaan diferensial yang memuat derivatif dari suatu variabel terhadap dua atau lebih variabel bebas. Persamaan ini berperan penting dalam menggambarkan fenomena fisis yang melibatkan besaran yang berubah terhadap ruang dan waktu, seperti gelombang elektromagnetik dan hidrodinamika. Makalah ini menjelaskan konsep dasar persamaan diferensial parsial, jenis-Fisika matematika diferensial parsial.pptx
Fisika matematika diferensial parsial.pptxzerobaeseu1
╠²
Dokumen ini membahas konsep turunan dalam matematika, termasuk aplikasi dan persamaan diferensial. Terdapat penjelasan mengenai turunan biasa dan diferensial parsial, beserta contoh soal untuk masing-masing. Pembelajaran ini penting dalam memahami fenomena alam dan memiliki aplikasi luas dalam evaluasi akademik.Turunan berarah dan gradien garis dalam fungsi.pptx
Turunan berarah dan gradien garis dalam fungsi.pptxRomdoni4
╠²
Dokumen ini membahas tentang konsep turunan dalam ruang berdimensi, mencakup turunan total untuk berbagai jumlah variabel dan definisi turunan parsial. Selain itu, dijelaskan juga tentang turunan berarah, gradien, dan penerapan aturan rantai dalam menghitung turunan fungsi komposisi. Contoh-contoh soal diberikan untuk memperjelas konsep yang dibahas.║▌║▌▀Ż-TSP102-Kalkulus-TSP-102-P12dasaspdf
║▌║▌▀Ż-TSP102-Kalkulus-TSP-102-P12dasaspdfArisWidyoNugroho
╠²
Dokumen ini membahas konsep turunan fungsi multivariabel dalam kalkulus, mencakup topik seperti turunan parsial, limit, dan kekontinuan. Mahasiswa diharapkan dapat memahami dan menghitung turunan dari fungsi dengan lebih dari satu variabel, serta menerapkan aturan rantai. Contoh-contoh dan problem set disediakan untuk melatih pemahaman tentang materi tersebut.Fisika matematika bab4 differensial danintegral
Fisika matematika bab4 differensial danintegralRozaq Fadlli
╠²
Bab 4 membahas konsep diferensial dan integral untuk fungsi satu dan lebih variabel. Differensial parsial digunakan untuk menentukan turunan fungsi multivariabel terhadap satu variabel dengan variabel lain dianggap konstan. Aplikasi diferensial parsial meliputi penentuan titik ekstremum dan jarak terdekat ke permukaan.Resmawan-Kalkulus-Turunan-Parsial.pdf
Resmawan-Kalkulus-Turunan-Parsial.pdfmisterx33
╠²
Dokumen ini adalah catatan tentang turunan parsial untuk fungsi dua dan tiga variabel, termasuk definisi, notasi, serta contoh dan solusi untuk berbagai latihan. Penjelasan mencakup bagaimana menghitung turunan parsial pertama dan kedua, serta konsep turunan parsial campuran. Juga dibahas aplikasi turunan parsial dalam konteks fungsi lebih dari dua variabel.Diferensial Parsial
Diferensial ParsialRose Nehe
╠²
Dokumen ini adalah tugas kelompok mengenai aplikasi persamaan diferensial parsial, disusun oleh mahasiswa program studi pendidikan matematika di Universitas Negeri Medan. Persamaan diferensial, yang melibatkan fungsi dan turunannya, memiliki banyak aplikasi dalam sains dan teknologi, dan penting dalam bidang rekayasa serta fisika. Tugas ini juga membahas definisi dan aplikasi dari turunan parsial.Termodinamika (1- 2) b diferensial_parsial
Termodinamika (1- 2) b diferensial_parsialjayamartha
╠²
Dokumen tersebut membahas tentang diferensial parsial dan elastisitas parsial dalam penyelesaian masalah ekonomi dan bisnis. Diferensial parsial adalah turunan fungsi lebih dari satu variabel dengan asumsi salah satu variabel dianggap konstan. Elastisitas parsial mengukur sensitivitas perubahan permintaan suatu barang terhadap perubahan harga barang lain.Fungsi beberapa varibel peubah banyak
Fungsi beberapa varibel peubah banyakMono Manullang
╠²
Dokumen ini membahas konsep dasar fungsi beberapa variabel, termasuk definisi, turunan parsial, dan teknik visualisasi seperti peta kontur dan kurva tingkat. Selain itu, terdapat penjelasan tentang cara menentukan titik kritis dan kondisi untuk ekstrim lokal pada fungsi dua variabel, serta aplikasi praktis dalam optimasi. Contoh yang digunakan mencakup penghitungan volume dan biaya pembuatan kotak serta pencarian nilai maksimum dan minimum dalam konteks fungsi.Makalah kalkulus lanjut
Makalah kalkulus lanjutEnggar Dewa
╠²
Bab ini membahas penyelesaian turunan parsial fungsi implisit dengan menggunakan aturan rantai. Metode pendiferensialan implisit digunakan untuk menentukan turunan fungsi yang didefinisikan secara implisit oleh persamaan F(x,y)=0. Turunan fungsi implisit dapat ditentukan untuk dua variabel maupun tiga variabel atau lebih. Contoh soal diberikan beserta penyelesaiannya untuk memperjelas konsep dasarTurunan Parsial.pdf
Turunan Parsial.pdfJoyaSaddani
╠²
Dokumen ini membahas tentang turunan parsial dan diferensial total dari fungsi dua variabel dalam matakuliah kalkulus. Terdapat pula contoh aplikasi dalam menghitung laju perubahan tekanan terhadap suhu berdasarkan hukum gas. Referensi yang digunakan termasuk buku karya James Stewart dan Purcell.FUNGSI-2-VAR.pdf
FUNGSI-2-VAR.pdfomriyad
╠²
Dokumen ini membahas tentang fungsi dua variabel, yang dituliskan dalam bentuk eksplisit dan implisit, serta menjelaskan tentang diferensial parsial untuk fungsi-fungsi tersebut. Berbagai contoh fungsi dan cara menentukan turunan parsial terhadap variabel x dan y juga diberikan. Selain itu, terdapat tugas untuk menghitung turunan parsial dari fungsi-fungsi yang diberikan, yang harus diselesaikan dan dikumpulkan pada tanggal yang telah ditentukan.Kalkulus
KalkulusRichy Krisna
╠²
Turunan fungsi implisit dapat ditentukan dengan memperlakukan variabel tak bebas sebagai fungsi eksplisit dari variabel bebas. Kemudian digunakan aturan rantai untuk mencari turunan fungsi tersebut. Contoh soal menunjukkan proses penentuan turunan fungsi implisit dengan mengasumsikan variabel tak bebas sebagai fungsi eksplisit lalu menerapkan aturan rantai.Ppt materi kpb bab 2
Ppt materi kpb bab 2HapizahFKIP
╠²
Dokumen ini menjelaskan tentang turunan parsial, yang merupakan fungsi dengan dua atau lebih variabel yang dihitung terhadap masing-masing variabel. Terdapat berbagai notasi untuk turunan parsial, serta konsep kemiringan garis singgung pada permukaan. Selain itu, dokumen juga membahas turunan parsial tingkat tinggi yang dapat diturunkan lebih dari sekali.Ppt materi kpb bab 4
Ppt materi kpb bab 4HapizahFKIP
╠²
Dokumen tersebut membahas konsep dasar diferensiasi dan diferensial total untuk fungsi satu dan lebih variabel, termasuk definisi keterdiferensiasian, linearitas lokal, hampiran diferensial total, dan syarat agar suatu persamaan diferensial bersifat eksak."Turunan.pptx
Turunan.pptxRoihan22
╠²
Dokumen tersebut membahas tentang kecepatan saat, gradien garis singgung, dan definisi turunan fungsi. Kecepatan saat dan gradien garis singgung merupakan bentuk limit yang sama yang juga muncul pada masalah lainnya. Turunan fungsi adalah fungsi f' yang nilainya pada bilangan c adalah limit dari turunan fungsi tersebut ketika h mendekati nol.TURUNAN PARSIAL
TURUNAN PARSIALMAFIA '11
╠²
Teks tersebut membahas tentang turunan parsial dan diferensial total dari fungsi dengan lebih dari satu variabel. Turunan parsial digunakan untuk menghitung perubahan fungsi terhadap satu variabel saja dengan variabel lain dianggap konstan. Diferensial total melibatkan perubahan fungsi akibat perubahan semua variabel sekaligus. Konsep ini digunakan untuk menganalisis masalah ekstrem pada fungsi dengan banyak variabel.7. Perbaikan Fungsi Dua Peubah, Peta Kontur dan Turunan Parsial (1).pdf
7. Perbaikan Fungsi Dua Peubah, Peta Kontur dan Turunan Parsial (1).pdfMuhammadMiqdad17
╠²
Dokumen ini membahas tentang fungsi dua variabel, turunan parsial, dan kurva ketinggian serta peta kontur dari suatu fungsi dua variabel.Paper turunan
Paper turunanMiftakul Sururi
╠²
Turunan fungsi adalah fungsi lain yang menunjukkan tingkat perubahan suatu fungsi. Turunan digunakan untuk menyelesaikan masalah geometri dan mekanika seperti garis singgung dan kecepatan. Bab ini menjelaskan definisi turunan, aturan-aturan dasar untuk mencari turunan, turunan fungsi trigonometri, aturan rantai, dan diferensiasi implisit.Word
WordRahma Sari
╠²
Dokumen ini adalah modul kalkulus tipe B yang membahas aturan rantai dalam diferensiasi fungsi komposisi. Modul ini mencakup contoh-contoh dan penyelesaian terkait turunan parsial dengan fungsi variabel, serta penerapan aturan rantai pada fungsi implisit. Disusun oleh Fella Elsa Rahmasari untuk kelas 3F di Universitas PGRI Semarang.Diferensial
DiferensialNounna Monalisa
╠²
Persamaan diferensial parsial (PDP) adalah persamaan yang melibatkan fungsi dari beberapa variabel bebas dan turunan parsialnya, digunakan dalam berbagai aplikasi matematis dan fisika seperti penjalaran suara dan panas. Persamaan diferensial biasa, di sisi lain, melibatkan fungsi dari satu variabel dan turunan terhadap variabel tersebut, dengan banyak kontribusi dari matematikawan terkenal. Kalkulus diferensial juga memainkan peran penting dalam menjelaskan perubahan kuantitatif dan memiliki aplikasi luas dalam berbagai bidang, termasuk fisika dan optimisasi.5_Kalkulus_Turunan_(1)[1].pptx
5_Kalkulus_Turunan_(1)[1].pptxRaffiRaffiAhmadMaula
╠²
Dokumen ini membahas konsep turunan fungsi dan aplikasinya dalam kecepatan sesaat serta gradien garis singgung. Istilah-istilah kunci seperti limit, notasi turunan, dan teorema turunan dijelaskan dengan contoh praktis serta penurunan fungsi menggunakan aturan rantai. Penjelasan juga mencakup turunan implisit dan fungsi parametrik, serta turunan fungsi trigonometri.04 turunan
04 turunanRudi Wicaksana
╠²
Turunan fungsi trigonometri memiliki aturan khusus. Turunan sin(x) adalah cos(x), turunan cos(x) adalah -sin(x). Turunan fungsi trigonometri lainnya dapat ditentukan dengan menggunakan rumus turunan bentuk u/v.Matek topik 12_13_14_joel
Matek topik 12_13_14_joelhartantoahock
╠²
Dokumen tersebut membahas konsep-konsep dasar ekonomi mikro seperti diferensial fungsi majemuk, optimalisasi, permintaan marjinal, dan elastisitas permintaan. Secara ringkas, dokumen tersebut menjelaskan cara menghitung turunan parsial dan derivatif dari suatu fungsi, metode optimalisasi bersyarat melalui substitusi dan Lagrange, serta konsep permintaan marjinal dan elastisitas permintaan untuk menganalisis hubungan antar variabel.Turunan merupakan salah satu materi lanjutan dari limit fungsi.
Turunan merupakan salah satu materi lanjutan dari limit fungsi.MunajiMoena
╠²
Dokumen ini membahas konsep turunan dalam kalkulus, termasuk pengertian, aturan, dan metode menghitung turunan dari berbagai jenis fungsi, seperti fungsi trigonometri dan fungsi implisit. Juga dijelaskan penggunaan turunan untuk menemukan garis singgung, laju perubahan, dan aplikasi dalam masalah nyata. Selain itu, terdapat contoh-contoh praktis yang menunjukkan penerapan definisi dan aturan turunan.Modul Ajar B Indonesia Kelas 7 Deep Learning
Modul Ajar B Indonesia Kelas 7 Deep LearningAdm Guru
╠²
Modul ajar dengan metode pembelajaran Deep Learning yaitu Meaningful Learning, Mindful Learning, dan Joyful LearningPRESENTASI Tentang Dunia Usaha dan juga Manfaat komputer dalam Dunia Usaha
PRESENTASI Tentang Dunia Usaha dan juga Manfaat komputer dalam Dunia Usahafebrianalkadir123
╠²
ini adalah presentasi tentang dunia usaha, dibuatnya presentasi ini adalah untuk memenuhi tugas perkuliahan saya di mata kuliah Komputer dan Masyarakat. Dibuat nya presentasi ini agar memudahkan orang orang yang sedang mencari document .pptx yang bertemakan Dunia UsahaMore Related Content
Similar to Ringkasan Materi Turunan Parsial Matematika (20)
Resmawan-Kalkulus-Turunan-Parsial.pdf
Resmawan-Kalkulus-Turunan-Parsial.pdfmisterx33
╠²
Dokumen ini adalah catatan tentang turunan parsial untuk fungsi dua dan tiga variabel, termasuk definisi, notasi, serta contoh dan solusi untuk berbagai latihan. Penjelasan mencakup bagaimana menghitung turunan parsial pertama dan kedua, serta konsep turunan parsial campuran. Juga dibahas aplikasi turunan parsial dalam konteks fungsi lebih dari dua variabel.Diferensial Parsial
Diferensial ParsialRose Nehe
╠²
Dokumen ini adalah tugas kelompok mengenai aplikasi persamaan diferensial parsial, disusun oleh mahasiswa program studi pendidikan matematika di Universitas Negeri Medan. Persamaan diferensial, yang melibatkan fungsi dan turunannya, memiliki banyak aplikasi dalam sains dan teknologi, dan penting dalam bidang rekayasa serta fisika. Tugas ini juga membahas definisi dan aplikasi dari turunan parsial.Termodinamika (1- 2) b diferensial_parsial
Termodinamika (1- 2) b diferensial_parsialjayamartha
╠²
Dokumen tersebut membahas tentang diferensial parsial dan elastisitas parsial dalam penyelesaian masalah ekonomi dan bisnis. Diferensial parsial adalah turunan fungsi lebih dari satu variabel dengan asumsi salah satu variabel dianggap konstan. Elastisitas parsial mengukur sensitivitas perubahan permintaan suatu barang terhadap perubahan harga barang lain.Fungsi beberapa varibel peubah banyak
Fungsi beberapa varibel peubah banyakMono Manullang
╠²
Dokumen ini membahas konsep dasar fungsi beberapa variabel, termasuk definisi, turunan parsial, dan teknik visualisasi seperti peta kontur dan kurva tingkat. Selain itu, terdapat penjelasan tentang cara menentukan titik kritis dan kondisi untuk ekstrim lokal pada fungsi dua variabel, serta aplikasi praktis dalam optimasi. Contoh yang digunakan mencakup penghitungan volume dan biaya pembuatan kotak serta pencarian nilai maksimum dan minimum dalam konteks fungsi.Makalah kalkulus lanjut
Makalah kalkulus lanjutEnggar Dewa
╠²
Bab ini membahas penyelesaian turunan parsial fungsi implisit dengan menggunakan aturan rantai. Metode pendiferensialan implisit digunakan untuk menentukan turunan fungsi yang didefinisikan secara implisit oleh persamaan F(x,y)=0. Turunan fungsi implisit dapat ditentukan untuk dua variabel maupun tiga variabel atau lebih. Contoh soal diberikan beserta penyelesaiannya untuk memperjelas konsep dasarTurunan Parsial.pdf
Turunan Parsial.pdfJoyaSaddani
╠²
Dokumen ini membahas tentang turunan parsial dan diferensial total dari fungsi dua variabel dalam matakuliah kalkulus. Terdapat pula contoh aplikasi dalam menghitung laju perubahan tekanan terhadap suhu berdasarkan hukum gas. Referensi yang digunakan termasuk buku karya James Stewart dan Purcell.FUNGSI-2-VAR.pdf
FUNGSI-2-VAR.pdfomriyad
╠²
Dokumen ini membahas tentang fungsi dua variabel, yang dituliskan dalam bentuk eksplisit dan implisit, serta menjelaskan tentang diferensial parsial untuk fungsi-fungsi tersebut. Berbagai contoh fungsi dan cara menentukan turunan parsial terhadap variabel x dan y juga diberikan. Selain itu, terdapat tugas untuk menghitung turunan parsial dari fungsi-fungsi yang diberikan, yang harus diselesaikan dan dikumpulkan pada tanggal yang telah ditentukan.Kalkulus
KalkulusRichy Krisna
╠²
Turunan fungsi implisit dapat ditentukan dengan memperlakukan variabel tak bebas sebagai fungsi eksplisit dari variabel bebas. Kemudian digunakan aturan rantai untuk mencari turunan fungsi tersebut. Contoh soal menunjukkan proses penentuan turunan fungsi implisit dengan mengasumsikan variabel tak bebas sebagai fungsi eksplisit lalu menerapkan aturan rantai.Ppt materi kpb bab 2
Ppt materi kpb bab 2HapizahFKIP
╠²
Dokumen ini menjelaskan tentang turunan parsial, yang merupakan fungsi dengan dua atau lebih variabel yang dihitung terhadap masing-masing variabel. Terdapat berbagai notasi untuk turunan parsial, serta konsep kemiringan garis singgung pada permukaan. Selain itu, dokumen juga membahas turunan parsial tingkat tinggi yang dapat diturunkan lebih dari sekali.Ppt materi kpb bab 4
Ppt materi kpb bab 4HapizahFKIP
╠²
Dokumen tersebut membahas konsep dasar diferensiasi dan diferensial total untuk fungsi satu dan lebih variabel, termasuk definisi keterdiferensiasian, linearitas lokal, hampiran diferensial total, dan syarat agar suatu persamaan diferensial bersifat eksak."Turunan.pptx
Turunan.pptxRoihan22
╠²
Dokumen tersebut membahas tentang kecepatan saat, gradien garis singgung, dan definisi turunan fungsi. Kecepatan saat dan gradien garis singgung merupakan bentuk limit yang sama yang juga muncul pada masalah lainnya. Turunan fungsi adalah fungsi f' yang nilainya pada bilangan c adalah limit dari turunan fungsi tersebut ketika h mendekati nol.TURUNAN PARSIAL
TURUNAN PARSIALMAFIA '11
╠²
Teks tersebut membahas tentang turunan parsial dan diferensial total dari fungsi dengan lebih dari satu variabel. Turunan parsial digunakan untuk menghitung perubahan fungsi terhadap satu variabel saja dengan variabel lain dianggap konstan. Diferensial total melibatkan perubahan fungsi akibat perubahan semua variabel sekaligus. Konsep ini digunakan untuk menganalisis masalah ekstrem pada fungsi dengan banyak variabel.7. Perbaikan Fungsi Dua Peubah, Peta Kontur dan Turunan Parsial (1).pdf
7. Perbaikan Fungsi Dua Peubah, Peta Kontur dan Turunan Parsial (1).pdfMuhammadMiqdad17
╠²
Dokumen ini membahas tentang fungsi dua variabel, turunan parsial, dan kurva ketinggian serta peta kontur dari suatu fungsi dua variabel.Paper turunan
Paper turunanMiftakul Sururi
╠²
Turunan fungsi adalah fungsi lain yang menunjukkan tingkat perubahan suatu fungsi. Turunan digunakan untuk menyelesaikan masalah geometri dan mekanika seperti garis singgung dan kecepatan. Bab ini menjelaskan definisi turunan, aturan-aturan dasar untuk mencari turunan, turunan fungsi trigonometri, aturan rantai, dan diferensiasi implisit.Word
WordRahma Sari
╠²
Dokumen ini adalah modul kalkulus tipe B yang membahas aturan rantai dalam diferensiasi fungsi komposisi. Modul ini mencakup contoh-contoh dan penyelesaian terkait turunan parsial dengan fungsi variabel, serta penerapan aturan rantai pada fungsi implisit. Disusun oleh Fella Elsa Rahmasari untuk kelas 3F di Universitas PGRI Semarang.Diferensial
DiferensialNounna Monalisa
╠²
Persamaan diferensial parsial (PDP) adalah persamaan yang melibatkan fungsi dari beberapa variabel bebas dan turunan parsialnya, digunakan dalam berbagai aplikasi matematis dan fisika seperti penjalaran suara dan panas. Persamaan diferensial biasa, di sisi lain, melibatkan fungsi dari satu variabel dan turunan terhadap variabel tersebut, dengan banyak kontribusi dari matematikawan terkenal. Kalkulus diferensial juga memainkan peran penting dalam menjelaskan perubahan kuantitatif dan memiliki aplikasi luas dalam berbagai bidang, termasuk fisika dan optimisasi.5_Kalkulus_Turunan_(1)[1].pptx
5_Kalkulus_Turunan_(1)[1].pptxRaffiRaffiAhmadMaula
╠²
Dokumen ini membahas konsep turunan fungsi dan aplikasinya dalam kecepatan sesaat serta gradien garis singgung. Istilah-istilah kunci seperti limit, notasi turunan, dan teorema turunan dijelaskan dengan contoh praktis serta penurunan fungsi menggunakan aturan rantai. Penjelasan juga mencakup turunan implisit dan fungsi parametrik, serta turunan fungsi trigonometri.04 turunan
04 turunanRudi Wicaksana
╠²
Turunan fungsi trigonometri memiliki aturan khusus. Turunan sin(x) adalah cos(x), turunan cos(x) adalah -sin(x). Turunan fungsi trigonometri lainnya dapat ditentukan dengan menggunakan rumus turunan bentuk u/v.Matek topik 12_13_14_joel
Matek topik 12_13_14_joelhartantoahock
╠²
Dokumen tersebut membahas konsep-konsep dasar ekonomi mikro seperti diferensial fungsi majemuk, optimalisasi, permintaan marjinal, dan elastisitas permintaan. Secara ringkas, dokumen tersebut menjelaskan cara menghitung turunan parsial dan derivatif dari suatu fungsi, metode optimalisasi bersyarat melalui substitusi dan Lagrange, serta konsep permintaan marjinal dan elastisitas permintaan untuk menganalisis hubungan antar variabel.Turunan merupakan salah satu materi lanjutan dari limit fungsi.
Turunan merupakan salah satu materi lanjutan dari limit fungsi.MunajiMoena
╠²
Dokumen ini membahas konsep turunan dalam kalkulus, termasuk pengertian, aturan, dan metode menghitung turunan dari berbagai jenis fungsi, seperti fungsi trigonometri dan fungsi implisit. Juga dijelaskan penggunaan turunan untuk menemukan garis singgung, laju perubahan, dan aplikasi dalam masalah nyata. Selain itu, terdapat contoh-contoh praktis yang menunjukkan penerapan definisi dan aturan turunan.Recently uploaded (20)
Modul Ajar B Indonesia Kelas 7 Deep Learning
Modul Ajar B Indonesia Kelas 7 Deep LearningAdm Guru
╠²
Modul ajar dengan metode pembelajaran Deep Learning yaitu Meaningful Learning, Mindful Learning, dan Joyful LearningPRESENTASI Tentang Dunia Usaha dan juga Manfaat komputer dalam Dunia Usaha
PRESENTASI Tentang Dunia Usaha dan juga Manfaat komputer dalam Dunia Usahafebrianalkadir123
╠²
ini adalah presentasi tentang dunia usaha, dibuatnya presentasi ini adalah untuk memenuhi tugas perkuliahan saya di mata kuliah Komputer dan Masyarakat. Dibuat nya presentasi ini agar memudahkan orang orang yang sedang mencari document .pptx yang bertemakan Dunia UsahaBuku Panduan Peserta Uji Kompetensi Manajerial dan Sosial Kultural Tahun 2024...
Buku Panduan Peserta Uji Kompetensi Manajerial dan Sosial Kultural Tahun 2024...SaraswatiCyPrabowo
╠²
buku panduanSchool of Strategic Leaders: Mencetak Pemimpin Bangsa di Era Ketidakpastian G...
School of Strategic Leaders: Mencetak Pemimpin Bangsa di Era Ketidakpastian G...Dadang Solihin
╠²
School of Strategic Leaders bukan sekadar buku tentang teori kepemimpinan. Ia adalah cermin dari proses pembentukan dan pemantapan kepemimpinan strategis yang dilakukan secara sistematis, terukur, dan berlandaskan nilai-nilai Pancasila, UUD 1945, semangat Bhinneka Tunggal Ika, dan komitmen terhadap keutuhan Negara Kesatuan Republik Indonesia. Buku ini mengajak pembaca untuk menelusuri bagaimana Lemhannas RI, sebagai institusi negara yang berpengalaman dalam membentuk kader pemimpin bangsa, merancang dan menjalankan proses pendidikan kepemimpinan strategis yang utuh dan menyeluruh.
Kepemimpinan strategis bukanlah sekadar penguasaan atas kemampuan teknokratis, administratif, atau managerial. Kepemimpinan strategis adalah kemampuan untuk membayangkan masa depan, menyusun arah, dan memimpin transformasi bangsa dengan kesadaran penuh terhadap konteks geopolitik dan ketahanan nasional. Ia adalah seni mengelola ketidakpastian, keberagaman, konflik kepentingan, dan tantangan masa depan secara simultan, dengan mengedepankan nilai integritas, keberanian moral, kemampuan kolaboratif, serta kepekaan terhadap dinamika sosial dan budaya bangsa.
Dadang Solihin Policy Brief Jawa Tengah 2025
Dadang Solihin Policy Brief Jawa Tengah 2025Dadang Solihin
╠²
Dokumen ini disusun sebagai wujud kontribusi pemikiran strategis dalam menjembatani perencanaan pembangunan nasional dengan kebutuhan dan tantangan pembangunan daerah, khususnya di Provinsi Jawa Tengah dan kabupaten/kota di dalamnya.Tahap-Tahapan Penyusunan Laporan Keuangan Perusahaan_Pelatihan *Penyusunan LA...
Tahap-Tahapan Penyusunan Laporan Keuangan Perusahaan_Pelatihan *Penyusunan LA...Kanaidi ken
╠²
Narasumber/ Pemateri Training: Kanaidi, SE., M.Si., cSAP., CBCM
HP/Wa Kanaidi: 0812 2353 284,
e-mail : kanaidi63@gmail.com
-------------------------------------------Modul Ajar Matematika Kelas 8 Deep Learning
Modul Ajar Matematika Kelas 8 Deep LearningAdm Guru
╠²
Modul ajar dengan metode pembelajaran Deep Learning yaitu Meaningful Learning, Mindful Learning, dan Joyful LearningModul Ajar IPS Kelas 8 Deep Learning
Modul Ajar IPS Kelas 8 Deep LearningAdm Guru
╠²
Modul ajar dengan metode pembelajaran Deep Learning yaitu Meaningful Learning, Mindful Learning, dan Joyful LearningModul Ajar B Indonesia Kelas 8 Deep Learning
Modul Ajar B Indonesia Kelas 8 Deep LearningAdm Guru
╠²
Modul ajar dengan metode pembelajaran Deep Learning yaitu Meaningful Learning, Mindful Learning, dan Joyful LearningModul Ajar Prakarya Pengolahan Kelas 10 SMA/MA Fase E Kurikulum Merdeka
Modul Ajar Prakarya Pengolahan Kelas 10 SMA/MA Fase E Kurikulum MerdekaModul Kelas
╠²
Modul Ajar Prakarya Pengolahan Kelas 10 Fase E Kurikulum Merdeka [MODULKELAS.COM]Training Motivasi Menggapai Ridha Allah, Orang Tua dan Guru dalam Meraih Suks...
Training Motivasi Menggapai Ridha Allah, Orang Tua dan Guru dalam Meraih Suks...Namin AB Ibnu Solihin
╠²
Training Motivasi Menggapai Ridha Allah, Orang Tua dan Guru dalam Meraih Sukses Masa Depan Gemilang 2025 - Bersama Namin AB Ibnu SolihinOverview_PSAK & IFRS: Penyusunan Laporan Keuangan_Pelatihan *Penyusunan LAPOR...
Overview_PSAK & IFRS: Penyusunan Laporan Keuangan_Pelatihan *Penyusunan LAPOR...Kanaidi ken
╠²
Narasumber/ Pemateri Training: Kanaidi, SE., M.Si., cSAP., CBCM
HP/Wa Kanaidi: 0812 2353 284,
e-mail : kanaidi63@gmail.com
-------------------------------------------PUBLIC SPEAKING BNNK DEPOK 11 JUNI 2024.pptx
PUBLIC SPEAKING BNNK DEPOK 11 JUNI 2024.pptxDedi Dwitagama
╠²
DIPERSIAPKAN UNTUK PELATIHAN PENYULUH, RELAWAN ANTI NARKOBA KELURAHAN TANAH BARU DEPOK, DISELENGGARAKAN OLEH BNNK DEPOK DI RUMAH KERAMIK F. WIDAYANTO DEPOKModul Ajar Matematika Kelas 7 Deep Learning
Modul Ajar Matematika Kelas 7 Deep LearningAdm Guru
╠²
Modul ajar dengan metode pembelajaran Deep Learning yaitu Meaningful Learning, Mindful Learning, dan Joyful LearningSOSIALISASI PBG dan SLF Kota Madiun - STR - Rosyid Fix.pptx
SOSIALISASI PBG dan SLF Kota Madiun - STR - Rosyid Fix.pptxDinas Penanaman Modal dan Pelayanan Terpadu Satu Pintu Kota Madiun
╠²
SOSIALISASI PBG dan SLF Kota Madiun - STR - Rosyid Fix.pptxEKSPOS KETUA POKJA 2024 KOTO TUO iv nagari.pptx
EKSPOS KETUA POKJA 2024 KOTO TUO iv nagari.pptxDwifatmarakhmatsumin
╠²
EKSPOS KETUA POKJA 2024 KOTO TUO iv nagari.pptxSejarah Terbentuknya DPC GMNI Muna Tahun 2018.pdf
Sejarah Terbentuknya DPC GMNI Muna Tahun 2018.pdfZulzaman GMNI
╠²
Dalam konteks lokal, DPC GMNI Kendari sebagai satu wilayah yang sama dan sebagai cabang yang sangat Progressif dan Revolusioner, juga terdekat
menginisiatifkan untuk terbentuknya cabang baru GMNI di Propinsi Sulawesi
Tenggara, yakni tepatnya di Kabupaten Muna.
Karena semangat pengurus DPC GMNI Kendari juga tidak terlepas dari
semangat dan kemauan para calon anggota yang berpikir nasionalis untuk
mengibarkan bendera dan panji-panji perjuangan GMNI di Kabupaten Muna. Melalui hasil rapat pengurus DPC GMNI Kendari tanggal 30 Desember 2017,
maka dengan menugaskan Zulzaman (Ketua DPC GMNI Kendari), Abdul Wahab
(Wakabid Kaderisasi DPC GMNI Kendari) beserta kawan-kawan untuk meninjau
lokasi kampus yang berada di Kabupaten Muna. Dan hasil yang didapatkan adalah
bertemu kawan-kawan mahasiswa (Intan Irianti) yang kuliah di kampus Akademi
Keperawatan Kabupaten Muna.Young Political Leaders: Menjawab Tantangan Zaman, Mengukir Masa Depan Bangsa
Young Political Leaders: Menjawab Tantangan Zaman, Mengukir Masa Depan BangsaDadang Solihin
╠²
Buku ini hadir sebagai bagian dari upaya strategis untuk mendorong tumbuhnya generasi pemimpin muda Indonesia yang tidak hanya cerdas secara intelektual, tetapi juga matang secara emosional dan kuat secara moral. Dalam buku ini dibahas sejumlah dimensi penting yang perlu dikuasai oleh para calon pemimpin politik muda, mulai dari pemahaman tentang tata kelola demokrasi, penguasaan isu-isu strategis nasional dan global, keterampilan komunikasi publik, hingga etika politik.
Lebih dari itu, buku ini juga menggarisbawahi pentingnya pendidikan politik yang transformatif. Pendidikan politik harus membentuk kesadaran kolektif bahwa kekuasaan bukan tujuan, melainkan sarana untuk mewujudkan keadilan sosial dan kesejahteraan masyarakat. Di sinilah pentingnya pembibitan kader politik muda dilakukan secara terstruktur dan berkelanjutan oleh berbagai institusi, baik partai politik, lembaga pendidikan, maupun organisasi masyarakat sipil.
Buku Panduan Peserta Uji Kompetensi Manajerial dan Sosial Kultural Tahun 2024...
Buku Panduan Peserta Uji Kompetensi Manajerial dan Sosial Kultural Tahun 2024...SaraswatiCyPrabowo
╠²
Training Motivasi Menggapai Ridha Allah, Orang Tua dan Guru dalam Meraih Suks...
Training Motivasi Menggapai Ridha Allah, Orang Tua dan Guru dalam Meraih Suks...Namin AB Ibnu Solihin
╠²
SOSIALISASI PBG dan SLF Kota Madiun - STR - Rosyid Fix.pptx
SOSIALISASI PBG dan SLF Kota Madiun - STR - Rosyid Fix.pptxDinas Penanaman Modal dan Pelayanan Terpadu Satu Pintu Kota Madiun
╠²
Ad
Ringkasan Materi Turunan Parsial Matematika
- 2. Turunan Parsial ŌĆó Misalkan z = f(x,y) fungsi 2 variabel yg terdefinisi disekitar titik (x,y). Turunan parsial dari f terhadap x adalah turunan z terhdp x dimana hanya variabel x saja yg diasumsikan berubah, dan y tetap konstan. Mengukur kecepatan perubahan z thdp x sementara y konstan. ŌĆó Turunan parsial z = f(x,y) terhdp x ditulis didefinisikan sbb. ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ ’Ć½ ’ĆĮ ’ĆĮ ’éČ ’éČ ’é« h y x f y h x f y x f y x f x h x ) , ( ) , ( lim ) , ( ) , ( 0 ) , ( ) , ( y x f y x f x z x x ’ĆĮ ’éČ ’éČ ’ĆĮ ’éČ ’éČ
- 3. ŌĆó Turunan parsial z = f(x,y) terhdp y ditulis didefinisikan sbb. Contoh: ) , ( ) , ( y x f y x f y z y y ’ĆĮ ’éČ ’éČ ’ĆĮ ’éČ ’éČ ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ ’Ć½ ’ĆĮ ’ĆĮ ’éČ ’éČ ’é« k y x f k y x f y x f y x f y k y ) , ( ) , ( lim ) , ( ) , ( 0 ’Ć© ’Ć® . 2 2 lim 2 lim ] [ ] ) [( lim ) , ( ) , ( lim ) , ( x : Lengkapnya . 2 maka ) , ( 0 2 0 2 2 2 2 0 0 2 2 x h x h h xh h y x y h x h y x g y h x g y x g x z x y x y x g z h h h h ’ĆĮ ’Ć½ ’ĆĮ ’āĘ ’āĘ ’āĖ ’āČ ’ā¦ ’ā¦ ’ā© ’ā” ’Ć½ ’ĆĮ ’āĘ ’āĘ ’āĖ ’āČ ’ā¦ ’ā¦ ’ā© ’ā” ’Ć½ ’ĆŁ ’Ć½ ’Ć½ ’ĆĮ ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ ’Ć½ ’ĆĮ ’éČ ’éČ ’ĆĮ ’éČ ’éČ ’Ć½ ’ĆĮ ’ĆĮ ’é« ’é« ’é« ’é«
- 4. x f ’éČ ’éČ adalah turunan fungsi f(x,y) terhadap x dengan memperlakukan y sebagai suatu tetapan, yang disebut turunan parsial fungsi f(x,y) terhadap x adalah turunan fungsi f(x,y) terhadap x dengan memperlakukan y sebagai suatu tetapan, yang disebut turunan parsial fungsi f(x,y) terhadap y y f ’éČ ’éČ Lambang lain y f ’éČ ’éČ x f ’éČ ’éČ = fx (x,y) (1.a) = fy (x,y) (1.b)
- 5. xx f x f x f x ’é║ ’éČ ’éČ ’é║ ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’éČ ’éČ ’éČ ’éČ 2 2 yy f y f y f y ’é║ ’éČ ’éČ ’é║ ’āĘ ’āĘ ’āĖ ’āČ ’ā¦ ’ā¦ ’ā© ’ā” ’éČ ’éČ ’éČ ’éČ 2 2 yx f y x f y f x ’é║ ’éČ ’éČ ’éČ ’é║ ’āĘ ’āĘ ’āĖ ’āČ ’ā¦ ’ā¦ ’ā© ’ā” ’éČ ’éČ ’éČ ’éČ 2 Turunan parsial (1a) dan (1b) umumnya juga merupakan fungsi dari x dan y, maka jika diturunkan lebih lanjut, disebut turunan parsial kedua.
- 6. Contoh ) cos( 2 xy y y x f ’ĆŁ ’ĆĮ ’éČ ’éČ ) cos( 2 xy x xy y f ’ĆŁ ’ĆĮ ’éČ ’éČ xy x x xy x xy y y f y y f sin 2 )) cos( 2 ( 2 2 2 ’Ć½ ’ĆĮ ’ĆŁ ’éČ ’éČ ’ĆĮ ’āĘ ’āĘ ’āĖ ’āČ ’ā¦ ’ā¦ ’ā© ’ā” ’éČ ’éČ ’éČ ’éČ ’ĆĮ ’éČ ’éČ ’Ć© ’Ć® xy y xy y y x x f x x f sin ) cos( 2 2 2 2 ’ĆĮ ’ĆŁ ’éČ ’éČ ’ĆĮ ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’éČ ’éČ ’éČ ’éČ ’ĆĮ ’éČ ’éČ ’Ć© ’Ć® ) cos( cos 2 ) cos( 2 xy xy xy y xy y y y x f y ’Ć½ ’ĆŁ ’ĆĮ ’ĆŁ ’éČ ’éČ ’ĆĮ ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’éČ ’éČ ’éČ ’éČ ’Ć© ’Ć® ) cos( cos 2 ) cos( 2 xy xy xy y xy x xy x y f x ’Ć½ ’ĆŁ ’ĆĮ ’ĆŁ ’éČ ’éČ ’ĆĮ ’āĘ ’āĘ ’āĖ ’āČ ’ā¦ ’ā¦ ’ā© ’ā” ’éČ ’éČ ’éČ ’éČ ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’éČ ’éČ ’éČ ’éČ ’ĆĮ ’āĘ ’āĘ ’āĖ ’āČ ’ā¦ ’ā¦ ’ā© ’ā” ’éČ ’éČ ’éČ ’éČ x f y y f x Misalkan f(x,y)=xy2 ŌĆō sin (xy). Maka ..,
- 7. SOAL LATIHAN ŌĆó Tentukan turunan parsial fungsi-fungsi di bawah ini: 1. z = ln y x ’Ć½ 2. z = 36 ŌĆō x2 ŌĆō y2 3. z = 3 - ) sin( 1 y x ’Ć½ 4. z = xy2 ŌĆō 2x2 + 3y3 5. z = arc tan x y 6. F(x,y,z) = xy ŌĆō yz + xz 7. F(x,y,z) = 3 2 2 2 z y x ’Ć½ ’Ć½ 8. F(x,y,z) = sin (xy) ŌĆō 2e xy 9. F(x,y,z) = arc sin ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” z xy
- 8. Differensial Total Misal z = F(x,y), dan fungsi tersebut dapat diturunkan terhadap variable x dan y, maka diperoleh turuna parisal terhadap x dan turunan parsial terhadap y yang secara berturut- turut dinotasikan dengan x y x F x z ’éČ ’éČ ’ĆĮ ’éČ ’éČ ) , ( ------------- (1) dan y y x F y z ’éČ ’éČ ’ĆĮ ’éČ ’éČ ) , ( ------------- (2) Dari (1) dan (2) diperoleh: dx x y x F dz ’éČ ’éČ ’ĆĮ ) , ( dan dy y y x F dz ’éČ ’éČ ’ĆĮ ) , ( Jumlah diferensialnya diperoleh: dz = dx x y x F ’éČ ’éČ ) , ( + dy y y x F ’éČ ’éČ ) , ( Bentuk di atas disebut diferensial total.
- 9. Contoh : Hitunglah diferensial total fungsi pada f(x,y)=xy2 ŌĆō sin (xy). Jawab. fx = y2 ŌĆō y cos (xy) dan fy = 2xy - x cos (xy) Sehingga turunan totalnya : df = (y2 ŌĆō y cos (xy) )dx + (2xy - x cos (xy)dy
- 10. Aturan Rantai ŌĆó Misalkan x = g(t) dan y = h(t) fungsi terdeferensial, terdefinisi di t dan misalkan z = f(x,y) mempunyai turunan parsial orde-satu yg kontinu. Maka z = f(x(t), y(t)) terdefinisi di t dan terdeferensial ŌĆó Contoh: dt dy y z dt dx x z dt dz ’éČ ’éČ ’Ć½ ’éČ ’éČ ’ĆĮ ? ; 3 2 ’ĆĮ ’ĆĮ ’ĆĮ ’ĆĮ dt dw t y t x e w xy
- 11. ŌĆó Mis. Z = f(u, v, x, y) dimana u dan v masing2 fungsi dari x dan y. Disini x dan y sebagai variabel antara dan variabel bebas. Aturan rantai menghasilkan: x f dx dv v f dx du u f dx dy y f dx dx x f dx dv v f dx du u f dx dz ’éČ ’éČ ’Ć½ ’éČ ’éČ ’Ć½ ’éČ ’éČ ’ĆĮ ’éČ ’éČ ’Ć½ ’éČ ’éČ ’Ć½ ’éČ ’éČ ’Ć½ ’éČ ’éČ ’ĆĮ
- 12. Contoh: Diketahui u= x2 + y2 ; x= re s ; dan y= re ŌĆōs Maka tentukanlah: ØææØæó ØææØæź , ØææØæó ØææØæ” , ØææØæź ØææØæ¤ , ØææØæź ØææØæĀ , ØææØæ” ØææØæ¤ , ØææØæ” ØææØæĀ , ØææØæó ØææØæ¤ , dan ØææØæó ØææØæĀ Jawab: ØææØæó ØææØæź = 2x ØææØæó ØææØæ” = 2y ØææØæź ØææØæ¤ = es ØææØæ” ØææØæ¤ = e-s ØææØæź ØææØæĀ = res ØææØæ” ØææØæĀ = - re-s ØææØæó ØææØæ¤ = ØææØæó ØææØæź ØææØæź ØææØæ¤ + ØææØæó ØææØæ” ØææØæ” ØææØæ¤ =( 2x)(es ) + (2y)( e-s ) = 2xes + 2ye-s ØææØæó ØææØæĀ = ØææØæó ØææØæź ØææØæź ØææØæĀ + ØææØæó ØææØæ” ØææØæ” ØææØæĀ =(2x)( res )+ (2y)( - re-s ) = 2x res - 2y re-s = r (2xes - 2ye- s