搁厂迟补苍と厂丑颈苍测厂迟补苍によるベイズ统计モデリング入门
71 likes37,550 views
第50回 TokyoR 発表資料 Stanコードは下のサイトで公開しております。 https://github.com/teuder/TokyoR50
![R で Stan
[ efS +bSU]SY e%U%sdefS t) seZ[ kefS
&&
RStan
RからStanを利用するインターフェース
インストール
ShinyStan
RStanの推定結果をいい感じに表示してくれる
（形式を合わせれば Stan 以外の MCMC ツールの結果も取り込める）
RStan Getting Started をみながらゴニョゴニョした後](https://image.slidesharecdn.com/tokyor50-150904231218-lva1-app6891/85/RStan-ShinyStan-21-320.jpg)
![階層ベイズモデル
y
a b[1]
s
普通のベイズ統計モデル 階層ベイズモデル
パラメターに対して、ハイパーパラメターを使って
（経験に基づいた）情報的な事前分布を設定する。
→パラメターに制約を課すことで推定が可能になる。
b[K]…
y
a b[1] b[K]…
無情報 無情報 無情報 無情報
無情報
パラメタ?数が多すぎると推定できない….
パラメター
観測値
ハイパー
パラメター](https://image.slidesharecdn.com/tokyor50-150904231218-lva1-app6891/85/RStan-ShinyStan-48-320.jpg)
![階層ベイズモデル
r
bSdS_RZ[ d 9* jfdSUf%X[fRZ[ d&
k+aTe 9* Z[ef%k) Td S]e:e c%-).--)Tk:.-&&
k+bdV 9* Z[ef%Ua E S e%bSdS_RZ[ d"kRZSf&)
Td S]e:e c%-).--)Tk:.-&&
b af%k+aTe"_[Ve) k+aTe"Uag fe) Ua :
T SU]
) bUZ:.6
) j ST:
) k ST:
&
ba[ fe%k+bdV"_[Ve) k+bdV"Uag fe) Ua :
d V
) bUZ:.6&
l
l+aTe 9* Z[ef%l) Td S]e:e c%*.2).2)Tk:/&&
l+bdV 9* Z[ef%Ua E S e%bSdS_RZ[ d"l&) Td S]e:e c%*.2).2)Tk:/&&
b af% l+aTe"_[Ve) l+aTe"Uag fe) Ua :
T SU]
) bUZ:.6
) j ST:
l
) k ST:
&
ba[ fe%l+bdV"_[Ve) l+bdV"Uag fe) Ua :
d V
) bUZ:.6&
テストの点数の分布へのあてはめ、各生徒の解答力の推定](https://image.slidesharecdn.com/tokyor50-150904231218-lva1-app6891/85/RStan-ShinyStan-58-320.jpg)
搁厂迟补苍と厂丑颈苍测厂迟补苍によるベイズ统计モデリング入门
- 2. アウトライン 統計モデルとは ベイズ推定 惭颁惭颁法 Stanの概要 R で Stan 統計モデルのデータへのあてはめ ShinyStanで結果の可視化 Stan文法 線形回帰モデル 階層ベイズモデル
- 4. ベイズ統計モデリング？ ベイズ統計 統計モデル y ～ f (x,θ)
- 5. ベイズ統計モデリング？ ベイズ統計 統計モデル y ～ f (x,θ)f (θ | y) ∝ f (y |θ) f (θ)
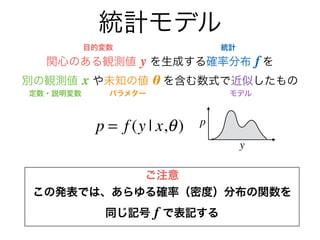
- 6. 統計モデル 関心のある観測値 y を生成する確率分布 f を 別の観測値 x や未知の値 θ を含む数式で近似したもの 現実によくフィットした統計モデルの発見は →将来発生する y の値の予測、観測できない量の推定 →現実の背景にある構造?法則性への理解につながる 定数?説明変数 パラメター 目的変数 統計 モデル p = f (y | x,θ) y p 面積1
- 7. 統計モデル 関心のある観測値 y を生成する確率分布 f を 別の観測値 x や未知の値 θ を含む数式で近似したもの 現実によくフィットした統計モデルの発見は →将来発生する y の値の予測、観測できない量の推定 →現実の背景にある構造?法則性への理解につながる 定数?説明変数 パラメター 目的変数 統計 モデル p = f (y | x,θ) y p ご注意 この発表では、あらゆる確率（密度）分布の関数を 同じ記号 f で表記する 面積1
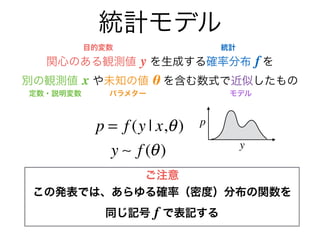
- 8. 統計モデル 関心のある観測値 y を生成する確率分布 f を 別の観測値 x や未知の値 θ を含む数式で近似したもの 現実によくフィットした統計モデルの発見は →将来発生する y の値の予測、観測できない量の推定 →現実の背景にある構造?法則性への理解につながる 定数?説明変数 パラメター 目的変数 統計 モデル p = f (y | x,θ) y p ご注意 この発表では、あらゆる確率（密度）分布の関数を 同じ記号 f で表記する y ～ f (x,θ) 面積1
- 9. 統計モデル p = f (y |θ) ↓ θ がある値の時に観測値 y が得られる確率 p (注1) 尤度が計算できる （注1）全ての観測値 y = {y1,...,yN} が同時に得られる確率
- 10. 統計モデル p = f (y |θ) ↓ θ がある値の時に観測値 y が得られる確率 p (注1) 尤度が計算できる （注1）全ての観測値 y = {y1,...,yN} が同時に得られる確率 尤度が大きくなるθの値からは 観測値と同じデータが得られやすいので 尤（もっと）もらしい値である y を定数として尤度を θ の関数とみなしたもの 尤度関数 L(θ) =
- 11. 統計モデルを観測値にあてはめる 最尤推定 ベイズ推定 ↓ 観測値 y が生成されやすいθの値を求める Stanはどちらにも対応している 尤度を最大化する θの値を求める 尤度と事前分布から θの事後確率分布を求める 正しいθの値は1つ あるθ値が正しい確率
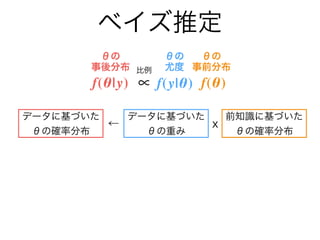
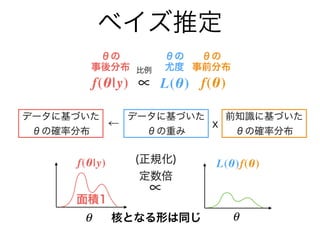
- 12. f(θ|y) ∝ f(θ)f(y|θ) ベイズ推定 θの 事後分布 θの 事前分布 θの 尤度比例 データに基づいた θの確率分布 データに基づいた θの重み 前知識に基づいた θの確率分布 x←
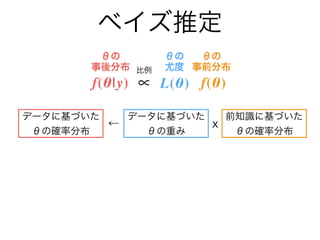
- 13. f(θ|y) ∝ f(θ)L(θ) ベイズ推定 θの 事後分布 θの 事前分布 θの 尤度比例 データに基づいた θの確率分布 データに基づいた θの重み 前知識に基づいた θの確率分布 x←
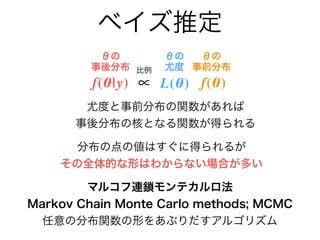
- 18. ベイズ推定 尤度と事前分布の関数があれば 事後分布の核となる関数が得られる f(θ|y) ∝ f(θ)L(θ) θの 事後分布 θの 事前分布 θの 尤度 分布の点の値はすぐに得られるが その全体的な形はわからない場合が多い マルコフ連鎖モンテカルロ法 Markov Chain Monte Carlo methods; MCMC 任意の分布関数の形をあぶりだすアルゴリズム 比例
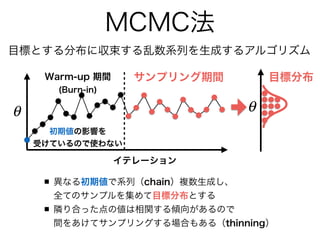
- 20. Stan Stan 記法により ユーザーが独自の統計モデルを記述できる が 実数のパラメターしか推定できない とはいえ離散パラメターを含むモデルも 工夫（周辺化）すれば推定できないわけではない（らしい） MCMCアルゴリズムとしてHMC(1), NUTS(2)を実装 目的の分布に素早く収束しやすい (1) ハミルトニアン?モンテカルロ法 (2) No-U-Tern Sampler
- 21. R で Stan [ efS +bSU]SY e%U%sdefS t) seZ[ kefS && RStan RからStanを利用するインターフェース インストール ShinyStan RStanの推定結果をいい感じに表示してくれる （形式を合わせれば Stan 以外の MCMC ツールの結果も取り込める） RStan Getting Started をみながらゴニョゴニョした後
- 22. 基本的なフロー Stanコード ↓ C++でコンパイル ↓ 推定実行 ↓ 収束診断 ↓ 推定結果 s_aV +efS t Sg UZReZ[ kefS %X[f& X[f 9* efS %s_aV +efS t&
- 23. 基本的なフロー Stanコード ↓ C++でコンパイル ↓ 推定実行 ↓ 収束診断 ↓ 推定結果 s_aV +efS t Sg UZReZ[ kefS %X[f& _aV 9* efS R_aV %s_aV +efS t& X[f 9* eS_b [ Y%_aV &?ベイズ推定 abf[_[l[ Y%_aV & 最尤推定
- 24. 基本的なフロー Stanコード ↓ C++でコンパイル ↓ 推定実行 ↓ 収束診断 ↓ 推定結果 s_aV +efS t Sg UZReZ[ kefS %X[f& _aV 9* efS R_aV %s_aV +efS t& X[f 9* eS_b [ Y%_aV &?ベイズ推定 abf[_[l[ Y%_aV & 最尤推定 defS Rabf[a e%SgfaRid[f : K & abf[a e%_U+Uad e : bSdS 77V f Uf>ad e%&&推定の並列化
- 25. はじめてのベイズ推定
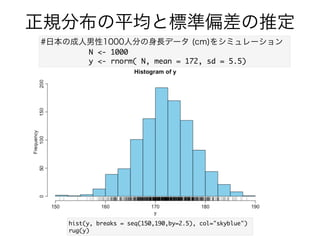
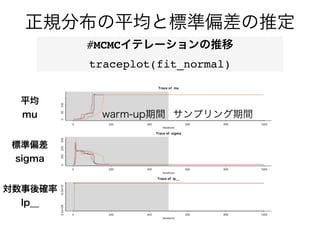
- 26. 正規分布の平均と標準偏差の推定 #日本の成人男性1000人分の身長データ (cm)をシミュレーション F 9* .--- k 9* d ad_% F) _ S : .4/) eV : 2+2& 身長cm 人数
- 27. VSfS m ,,IfS r [ f9 ai d:.; F8 ,, Fu、 rv d S kPF 8 ,, r k u F v n bSdS_ f de m ,, r d S _g8 ,, u rv d S 9 ai d:-; e[Y_S8 ,, “ u rp- v n _aV m ,, _g o ad_S % -) .---&8 ,, _g u v e[Y_S o ad_S % -) .---&8 ,,e[Y_S u v k o ad_S %_g) e[Y_S&8 ,, k u v n 正規分布の平均と標準偏差の推定 Stan ※Stanでは事前分布を指定しないと一様分布が指定される。
- 28. F 9* .--- k 9* d ad_% F) _ S : .4/) eV : 2+2& efS r ad_S RVSfS 9* [ef%F : F) k : k& r x X[fR ad_S 9* ,,efS X[f efS % X[ : ad_S +efS ,,efS ) VSfS : ad_S RVSfS ,, r ) [f d : /--- ,, r ) UZS[ e : 1 ,, ) fZ[ : . ,,fZ[ :/ . {~ ) iSd_ : X aad%[f d,/&& ,,iSd_*gb MCMCサンプル数 = (iter - warm)*chain*(1/thin) = 4000 正規分布の平均と標準偏差の推定 R
- 31. #パラメターの推定値の表示 print(fit_normal) B X d U Xad IfS _aV 7 ad_S + 1 UZS[ e) SUZ i[fZ [f d:/---8 iSd_gb:.---8 fZ[ :.8 baef*iSd_gb VdSie b d UZS[ :.---) fafS baef*iSd_gb VdSie:1---+ _ S e R_ S eV /+2# /2# 2-# 42# 64+2# R XX ZSf _g .4/+06 -+-- -+.4 .4/+-2 .4/+/5 .4/+06 .4/+2. .4/+40 /163 . e[Y_S 2+11 -+-- -+./ 2+/. 2+02 2+11 2+2/ 2+34 /004 . bRR */.6-+-0 -+-0 .+-2 */.6/+5/ */.6-+06 */.56+4- */.56+0- */.56+-2 ..6- . IS_b e i d VdSi ge[ Y FK I%V[SYR & Sf Ea <gY 0. .27-27-. /-.2+ Aad SUZ bSdS_ f d) R XX [e S UdgV _ Segd aX XX Uf[h eS_b e[l ) S V ZSf [e fZ baf f[S eUS d VgUf[a XSUfad a eb [f UZS[ e %Sf Ua h dY U ) ZSf:.&+ MCMCサンプルの 平均、平均の標準誤差、標準偏差、x%値、有効サンプル数、 ?R 正規分布の平均と標準偏差の推定
- 32. 正規分布の平均と標準偏差の推定 jfdSUf% aT Uf : FKDD efS X[f ) bSde : FKDD y r ) b d_gf V : A<DI r ） ) [ URiSd_gb : A<DI & iSd_*gb #サンプルされたパラメター値の抽出 bSdS_R ad_S 9* jfdSUf%X[fR ad_S & _g _ S % bSdS_R ad_S "_g & .4/+0602
- 34. ShinyStanの起動 [TdSdk%eZ[ kefS & eeaR ad_S 9* Sg UZReZ[ kefS %X[fR ad_S &
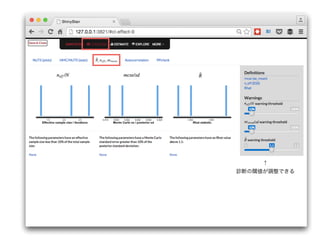
- 37. ↑ 診断の閾値が調整できる
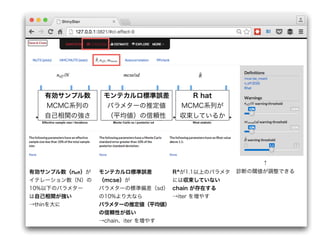
- 38. ↑ 診断の閾値が調整できる有効サンプル数（ne?）が イテレーション数（N）の 10%以下のパラメター は自己相関が強い →thinを大に R^が1.1以上のパラメタ には収束していない chain が存在する →iter を増やす モンテカルロ標準誤差 （mcse）が パラメターの標準偏差（sd） の10%より大なら パラメターの推定値（平均値） の信頼性が低い →chain、iter を増やす 有効サンプル数 MCMC系列の 自己相関の強さ モンテカルロ標準誤差 パラメターの推定値 （平均値）の信頼性 R hat MCMC系列が 収束しているか
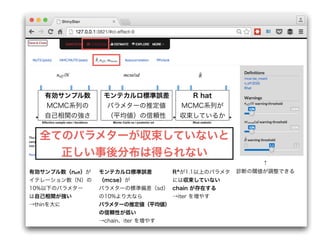
- 39. ↑ 診断の閾値が調整できる 全てのパラメターが収束していないと 正しい事後分布は得られない 有効サンプル数（ne?）が イテレーション数（N）の 10%以下のパラメター は自己相関が強い →thinを大に R^が1.1以上のパラメタ には収束していない chain が存在する →iter を増やす モンテカルロ標準誤差 （mcse）が パラメターの標準偏差（sd） の10%より大なら パラメターの推定値（平均値） の信頼性が低い →chain、iter を増やす 有効サンプル数 MCMC系列の 自己相関の強さ モンテカルロ標準誤差 パラメターの推定値 （平均値）の信頼性 R hat MCMC系列が 収束しているか
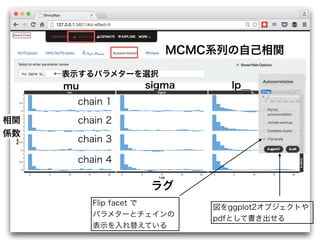
- 40. MCMC系列の自己相関 ←表示するパラメターを選択 mu sigma lp__ chain 1 chain 2 chain 3 chain 4 Flip facet で パラメターとチェインの 表示を入れ替えている 図をggplot2オブジェクトや pdfとして書き出せる ラグ 相関 係数
- 41. 厂迟补苍の文法
- 42. Stanコードの構成 Xg Uf[a e mn ,, VSfS mn ,,IfS r fdS eXad_ V VSfSmn ,, r bSdS_ f de mn ,, r fdS eXad_ V bSdS_ f demn ,, r _aV mn ,, Y dSf V cgS f[f[ e mn ,, r ,, 必須なのは _aV のみ、ブロックの順番を変えてはいけない bSdS_ f de) fdS eXad_ V bSdS_ f de) Y dSf V cgS f[f[ e ? で定義した値が出力される fdS eXad_ V bSdS_ f de 以降がイテレーション毎に実行される
- 43. 基本的なデータ型 ,, r [ f <8 ,,、 d S =8 ,, ,, q u p ~ v h UfadP.- L8 ,, _Sfd[jP<)< E8 ,, daiRh UfadP.- L/8 ,, ,, u v [ f9 ai d:.; >8 d S 9 ai d:-) gbb d:.-; 8 h Ufad9 ai d:_[ %L&) gbb d:_Sj%L&; 8 ,, u ~ v [ f MPF 8 ,,. 、 d S NP/)/)/ 8 ,,0 _Sfd[jP/)/ P0)0 8 ,,/j/ p0j0 ,,w
- 44. model ブロック _aV m _g o ad_S %-) .---&8 ,, e[Y_S o g [Xad_%-) .---&8 ,, k o ad_S %_g) e[Y_S&8 ,, u v n 実際には対数確率をひたすら足し上げている パラメタと観測値の分布を指定する f(θ|y) = C×f(y|θ)f(θ) log(f(θ|y)) = log(C)+log(f(y|θ))+log(f(θ)) HMCは対数事後確率関数をθで微分した傾きを利用するので θに依存しない定数項は省略されてる場合もある （log(C)やf(θ)内の正規化係数など）
- 45. model ブロック k o ZaY %fZ fS&8 //Sampling Statement [ Ud _ fR aYRbdaT% ZaY R aY% k) fZ fS& &8 bRR 9* bRR ( ZaY R aY% k) fZ fS &8w Stanでは 確率分布関数 hoge に対して 対数確率を足し上げる３つの等価な書き方がある aY% ZaY %& & ー Sampling Statement が使えない時は [ Ud _ fR aYRbdaT% & ※lp__ は将来的にはなくなるので推奨されない
- 46. モデルの记述例
- 47. 線形回帰 VSfS m [ f9 ai d:-; F8 ,, [ f9 ai d:.; C8 ,, ? ” _Sfd[jPF)C j8 ,, ? ” h UfadPF k8 ,, ” n bSdS_ f de m d S S bZS8 ,, （ h UfadPC T fS8 ,, r d S 9 ai d:-; e[Y_S8 ,, “ n _aV m ,, k o ad_S %S bZS ( j T fS) e[Y_S&8 ,, ~ ,,Xad%[ [ .7F& ,, kP[ o ad_S %S bZS ( jP[ T fS) e[Y_S&8 n
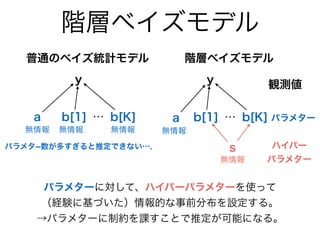
- 48. 階層ベイズモデル y a b[1] s 普通のベイズ統計モデル 階層ベイズモデル パラメターに対して、ハイパーパラメターを使って （経験に基づいた）情報的な事前分布を設定する。 →パラメターに制約を課すことで推定が可能になる。 b[K]… y a b[1] b[K]… 無情報 無情報 無情報 無情報 無情報 パラメタ?数が多すぎると推定できない…. パラメター 観測値 ハイパー パラメター
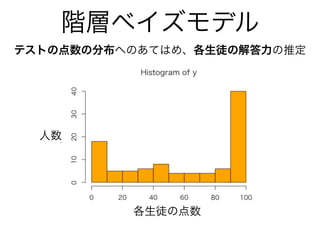
- 50. テストの点数の分布へのあてはめ、各生徒の解答力の推定 VSfS m [ f9 ai d:-; F8 ,, F [ f9 ai d:-; E8 ,, E [ f9 ai d:-; kPF 8 ,, k n bSdS_ f de m d S 9 ai d:-; S bZS8 ,, S bZS d S T fSPF 8 ,, T fS d S 9 ai d:-; e[Y_S8 ,,T fS “ e[Y_S n fdS eXad_ V bSdS_ f de m d S lPF 8 d S bPF 8 Xad%[ [ .7F& m lP[ 9* S bZS ( T fSP[ 8 ,, l bP[ 9* [ hR aY[f% lP[ &8 ,, }x b n n _aV m T fS o ad_S %-) e[Y_S&8 ,, u v Xad%[ [ .7F& kP[ o T[ a_[S %E) bP[ &8 ,, k u wv n ※ある問に正答する確率が p のとき、M個の問題のうち、 y 個正解する確率の分布
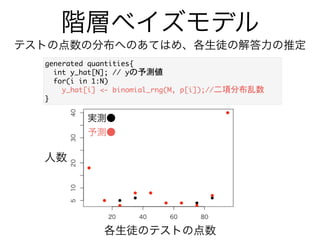
- 51. 階層ベイズモデル テストの点数の分布へのあてはめ、各生徒の解答力の推定 実測● 予測● 各生徒のテストの点数 人数 Y dSf V cgS f[f[ em [ f kRZSfPF 8 ,, k Xad%[ [ .7F& kRZSfP[ 9* T[ a_[S Rd Y%E) bP[ &8,, n
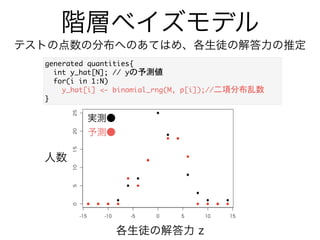
- 52. 階層ベイズモデル テストの点数の分布へのあてはめ、各生徒の解答力の推定 実測● 予測● 各生徒の解答力 z 人数 Y dSf V cgS f[f[ em [ f kRZSfPF 8 ,, k Xad%[ [ .7F& kRZSfP[ 9* T[ a_[S Rd Y%E) bP[ &8,, n
- 54. ベイズ統計モデリング入門書 道具としてのベイズ統計（涌井良幸） ベイズ統計、惭颁惭颁法 基礎からのベイズ統計学（豊田秀樹ら） ベイズ統計、ハミルトニアン?モンテカルロ法 データ解析のための統計モデリング入門（久保拓弥） 統計モデリング Stan Modeling Language Users Guide and Reference Manual Stanの使い方、ベイズ統計モデリング これで貴方も「ベイジアン」に！
- 55. ベイズ統計モデリング入門書 道具としてのベイズ統計（涌井良幸） ベイズ統計、惭颁惭颁法 基礎からのベイズ統計学（豊田秀樹ら） ベイズ統計、ハミルトニアン?モンテカルロ法 データ解析のための統計モデリング入門（久保拓弥） 統計モデリング Stan Modeling Language Users Guide and Reference Manual Stanの使い方、ベイズ統計モデリング これで貴方も「ベイジアン」に！ 超オススメ！ 俺俺Stan manual翻訳 by siero5335
- 57. 階層ベイズモデル r r aY[ef[U 9* Xg Uf[a %j&m.+-,%.( jb%*j&&n F 9* .-- E 9* .- S bZS 9* -+53 e[Y_S 9* 0+45 “ T fS 9* d ad_%F) _ S : -) eV : e[Y_S& l 9* S bZS ( T fS b 9* aY[ef[U%l& k 9* eSbb k%b) Xg Uf[a % &mdT[ a_%.) E) &n& efS r VSfSRZ[ d 9* [ef%F: YfZ%k&) E:.-) k:k& x X[fRZ[ d 9* efS %X[ : Z[ dSdUZ[US +efS ) VSfS : VSfSRZ[ d& テストの点数の分布へのあてはめ、各生徒の解答力の推定
- 58. 階層ベイズモデル r bSdS_RZ[ d 9* jfdSUf%X[fRZ[ d& k+aTe 9* Z[ef%k) Td S]e:e c%-).--)Tk:.-&& k+bdV 9* Z[ef%Ua E S e%bSdS_RZ[ d"kRZSf&) Td S]e:e c%-).--)Tk:.-&& b af%k+aTe"_[Ve) k+aTe"Uag fe) Ua : T SU] ) bUZ:.6 ) j ST: ) k ST: & ba[ fe%k+bdV"_[Ve) k+bdV"Uag fe) Ua : d V ) bUZ:.6& l l+aTe 9* Z[ef%l) Td S]e:e c%*.2).2)Tk:/&& l+bdV 9* Z[ef%Ua E S e%bSdS_RZ[ d"l&) Td S]e:e c%*.2).2)Tk:/&& b af% l+aTe"_[Ve) l+aTe"Uag fe) Ua : T SU] ) bUZ:.6 ) j ST: l ) k ST: & ba[ fe%l+bdV"_[Ve) l+bdV"Uag fe) Ua : d V ) bUZ:.6& テストの点数の分布へのあてはめ、各生徒の解答力の推定
- 59. 配列データへのアクセス ,,/j0 1j2 _Sfd[jP/)0 P1)2 8 ,, j. 9* P1)2)/)0 8 ,,d S j/ 9* P1)2)/ 8 ,,daiRh UfadP0 j0 9* P1)2 8 ,,_Sfd[jP/)0 j1 9* P1 8 ,,_Sfd[jP/)0 ,, 2 . ,,j2 9* P1)2) )0 ,,h UfadP/ z ~ ,, z Xad%[ [ .7/& j2P[ 9* P1)2)[)0 8 ,, z y ,, P. P/ P.)/
- 60. ロジスティック回帰 VSfS m [ f9 ai d:.; F8 ,, r [ f9 ai d:-; C8 ,, ? ” _Sfd[jPF)C j8 ,, [ f9 ai d:-) gbb d:.; kPF 8 ,, ” - ad .uw v n bSdS_ f de m d S S bZS8 ,, （ h UfadPC T fS8 ,, n _aV m k o T d ag [R aY[f%S bZS ( j T fS&8 ,, ~ ,,Xad % [ .7F& ,,kP o T d ag [%[ hR aY[f%S bZS ( T fS jP &&8 n （※注）ハマりポイント bernoulli（ベルヌーイ）分布は0か1（つまり整数）しか 返さないのに y を vector（実数）で定義してしまうと コンパイルエラーになる 線形回帰との違いを赤で示している ,,[ hR aY[f aY[ef[U
- 61. 予測値の算出① ,, $ VSfS m [ f9 ai d:-; F8 ,, [ f9 ai d:.; C8 ,, ? ” _Sfd[jPF)C j8 ,, ? ” u r v h UfadPF k8 ,, ” u r v ,, ? ” [ f9 ai d:-; FR i8 ,, _Sfd[jPFR i) C jR i8 ,,? ” u r v n bSdS_ f de m d S S bZS8 ,, （ h UfadPC T fS8 ,, r d S 9 ai d:-; e[Y_S8 ,, n _aV m k o ad_S %S bZS ( j T fS) e[Y_S&8 n Y dSf V cgS f[f[ e m h UfadPFR i kR i8 Xad % [ .7FR i& kR iP 9* ad_S Rd Y%jR iP T fS) e[Y_S&8 n Y dSf V cgS f[f[ e で算出する方法 可能な場合はこちらのほうが良い、有効サンプル数が大きくなる ,, r r y ,, k
- 62. 予測値の算出② ,, $ VSfS m [ f9 ai d:-; F8 ,, [ f9 ai d:.; C8 ,, ? ” _Sfd[jPF)C j8 ,, ? ” u r v h UfadPF k8 ,, ” u r v ,, ? ” [ f9 ai d:-; FR i8 ,, _Sfd[jPFR i) C jR i8 ,,? ” u r v n bSdS_ f de m d S S bZS8 ,, （ h UfadPC T fS8 ,, r d S 9 ai d:-; e[Y_S8 ,, ,, k r h UfadPFR i kR i8 n _aV m k o ad_S %S bZS ( j T fS) e[Y_S&8 ,, kR i o ad_S %S bZS ( j T fS) e[Y_S&8 n _aV で算出する方法