厂迟补苍勉强会资料(前编)
- 1. 厂迟补苍勉强会资料(前编) 2017/07/14 BDA研究会 専修大学大学院 文学研究科 北條大樹 Code: https://github.com/dastatis/Stan_Study
- 3. Rでベイズ推定するには?? 1. 自作コードを書く ? 長所???自分のモデルに合ったパラメータ推定が可能 ? 短所???汎用性が低い。ミスが起きやすい。書くまでに時間がかかる 2. パッケージを使う ? 長所???既存のモデルを用いてパラメータ推定が可能。 ? 短所???内部処理が不明。モデルの拡張ができない。 3. ベイズ推定ソフト(モジュール)を導入し、使う ? 長所???オーダーメイドモデルを作成可能。処理が明確。収束が速い。 ? 短所???覚えるまでに時間がかかる。ミスが起きやすい。
- 4. Rでベイズ推定するには?? 1. 自作コードを書く ? 長所???自分のモデルに合ったパラメータ推定が可能 ? 短所???汎用性が低い。ミスが起きやすい。書くまでに時間がかかる 2. パッケージを使う ? 長所???既存のモデルを用いてパラメータ推定が可能。 ? 短所???内部処理が不明。モデルの拡張ができない。 3. ベイズ推定ソフト(モジュール)を導入し、使う ? 長所???オーダーメイドモデルを作成可能。処理が明確。収束が速い。 ? 短所???覚えるまでに時間がかかる。ミスが起きやすい。 今日はベイズ推定ソフトを徹底的に覚える
- 5. Rにおけるベイズ推定ソフト ベイズ推定ソフトとは? MCMC(マルコフ連鎖モンテカルロ法)を用いて、 事後分布を得ることのできるソフトウェア 具体的なソフトウェア ? BUGS(Bayesian inference Using Gibbs Sampling) ? すべての始まり(既に開発は終了)。 ? JAGS(Just Another Gibbs Sampler) ? BUGSを使いやすくした感じ ? Stan (数学者 Stanislaw Ulamより) ? BUGSを進化させた感じ https://en.wikipedia.org/wiki/Stanislaw_Ulam
- 6. Stan ? 2010年頃にリリース。現在も随時アップデート中。 ? BDA3のAndrew Gelmanらによって設計 ? BUGS等で苦手としていた潜在変数モデリング(IRT)等における、 収束速度や推定精度の向上 ? 推定方法として、NUTSアルゴリズムに基づいたHMC法 (Hamiltonian Monte Carlo)を用いている(変分ベイズも導入)。
- 7. Stanの種類 ? 様々なインターフェイスに対応。Rでなくても良い ? Stanの記法は、各インターフェイス間で共通 ? 以降は搁厂迟补苍を厂迟补苍として绍介
- 9. Stanで分析するときの流れ(R) データ読み込み→read.csv() データ成形→dplyr 等々 みなさまのお好みの方法で 分析設定→data <- list() 分析実行→stan() data{ } parameters{ } model{ } 結果表示?可視化→summary() ggplot2
- 10. 【番外編】Stanで分析するときの流れ(Python) データ読み込み?データ成形 分析設定→data は ディクショナリー型で入れる 分析実行→stan() data{ } parameters{ } model{ } 結果表示?可視化? fit.plot()
- 11. Stanをうごかすためには? 用意するもの ? R ? Rstudio ? Rtools(Windows) or Xcode(Mac) ? Stan (“rstan” package) Stanを動かす( Rstan ? Rtools or Xcode(C++) ) ↑ RからStanを動かす命令を送る( R ? RStan ) ↑ Rに命令を送る( Rstudio ? R )
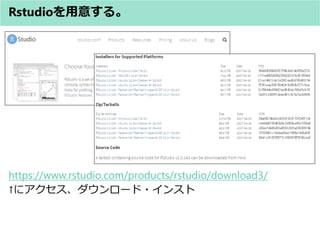
- 12. Rを用意する。 https://cran.ism.ac.jp/ ↑アクセス、Download R for 各翱厂からダウンロード&补尘辫;インスト
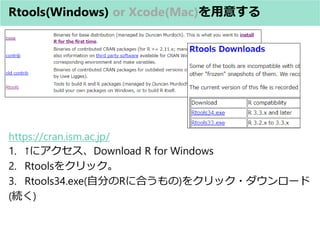
- 14. Rtools(Windows) or Xcode(Mac)を用意する https://cran.ism.ac.jp/ 1. ↑にアクセス、Download R for Windows 2. Rtoolsをクリック。 3. Rtools34.exe(自分のRに合うもの)をクリック?ダウンロード (続く)
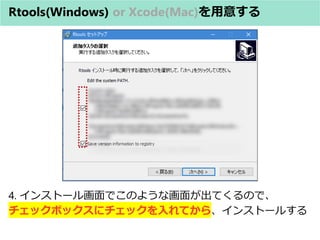
- 15. Rtools(Windows) or Xcode(Mac)を用意する 4. インストール画面でこのような画面が出てくるので、 チェックボックスにチェックを入れてから、インストールする
- 17. Stan (“rstan” package) を用意する。 ? Rstudioを起動する。 ? Consoleに install.packages(“rstan”) を入力し、実行。 (rstan)はすべて半角小文字 ? 下が表示されればインストールOK
- 18. ここまでまとめ ? 今回、Rでベイズ推定するためにStanというものを使う。 ? StanはRの世界では動かない。RはStanの世界では動かない。 ?StanとRの内的処理は、“別々の世界”で行われている。 ? RとStanの橋渡しのためにRstudioがあると便利。橋渡しその ものは、rstanパッケージを使う。 ? RstudioでRからStanに命令を送ったあと、PCそのもの(C++)に 命令を認識させる(変換する)必要がある。そのためにRtools & Xcodeを使う。
- 20. # R library(rstan) # rstan_options(auto_write = TRUE) # options(mc.cores = parallel::detectCores()) ? 赤枠をコメントアウトして( #を取って ) 実行すると、 読み込んだモデルを保存しておき、 並列処理化することができる(とりあえずここではしない) とりあえずStanをうごかす1 ( binomial.R )
- 21. # R model <- ' data{ int N; int Y; } parameters{ real<lower=0, upper=1> theta; } model{ Y ~ binomial(N, theta); } ' ? モデルを読み込む。今は何も考えず実行してみてください。 とりあえずStanをうごかす1 ここでうまくいかない場合。シングルクォーテーション ’ を 打ち直して見て下さい。コピーだと全角になることがあるよ うです。
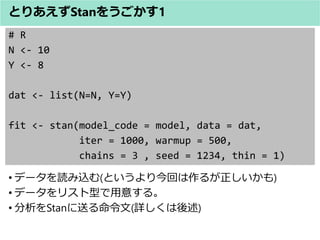
- 22. # R N <- 10 Y <- 8 dat <- list(N=N, Y=Y) fit <- stan(model_code = model, data = dat, iter = 1000, warmup = 500, chains = 3 , seed = 1234, thin = 1) ? データを読み込む(というより今回は作るが正しいかも) ? データをリスト型で用意する。 ? 分析をStanに送る命令文(詳しくは後述) とりあえずStanをうごかす1
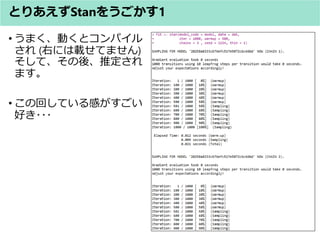
- 23. ? うまく、動くとコンパイル され (右には載せてません) そして、その後、推定され ます。 ? この回している感がすごい 好き??? とりあえずStanをうごかす1
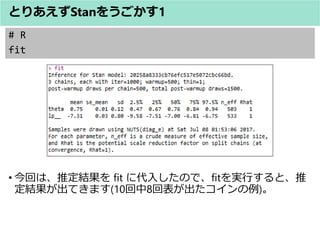
- 24. # R fit ? 今回は、推定結果を fit に代入したので、fitを実行すると、推 定結果が出てきます(10回中8回表が出たコインの例)。 とりあえずStanをうごかす1
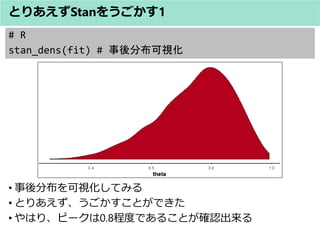
- 25. # R stan_dens(fit) # 事後分布可視化 ? 事後分布を可視化してみる ? とりあえず、うごかすことができた ? やはり、ピークは0.8程度であることが確認出来る とりあえずStanをうごかす1
- 26. library("rstan") model <- ' data{ int N; int Y; } parameters{ real<lower=0, upper=1> theta; } model{ Y ~ binomial(N, theta); } '#(右上に続く) ここまでのコード #(左下から) N <- 10 Y <- 8 dat <- list(N=N, Y=Y) fit <- stan(model_code = model, data = dat, iter = 1000, warmup = 500, chains = 3 , seed = 1234, thin = 1) fit stan_dens(fit) # 事後分布可視化
- 27. ? ここまでのRコードがどんなことをしているのか? ? Stanに何をさせているのか? を読み解いていく。 まずは、読み込み。これは問題ない。 ここまでのコードを読み解く # R library(rstan) # rstan_options(auto_write = TRUE) # options(mc.cores = parallel::detectCores())
- 28. # R model <- ' data{ int N; int Y; } parameters{ real<lower=0, upper=1> theta; } model{ Y ~ binomial(N, theta); } ' ? これが、ベイズモデルにあたる部分 ? これさえ書ければ、何でも推定できる ? 今回は、Rコードに直接記述する方法でモデルを書いた。 ここまでのコードを読み解く
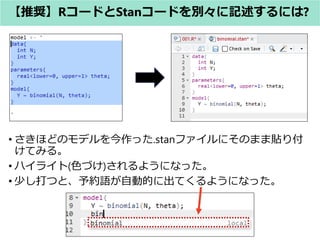
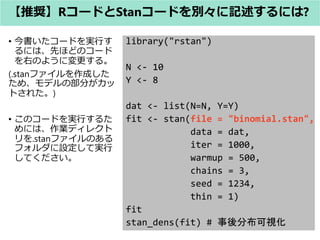
- 29. # R (.R file) library(rstan) model <- ‘ 略 ‘ data <- list() fit <- stan(model) ? コードを一括管理 できる。 ? コード全体がとて も長くなる。 ? 複数のモデルを比 較するのが大変 Rコードに直接記述する方法とは? 直接記述する方法 # R (.R file) library(rstan) data <- list() fit <- stan(.stan) 【推奨】RコードとStanコードを別々に記述する方法 # Stan(.stan file) data{ } parameters{ } model{ } ? コードを分けるため、モデルを複数比 較する際、管理しやすい。 ? モデルの使い回しが容易に行える(モデ ルコード単位で管理しているため) ? 簡単にモデルを書くことができる (Rstudioのハイライトが使えるため)
- 30. 【推奨】RコードとStanコードを別々に記述するには? もしくはCtrl + Shift + N もしくはCtrl + S モデル名.stan で保存 無事Stanファイルができていれば、右下がStanになる。 これでStanモデル用のハイライトが使える。 .stan ファイルを作成する
- 31. ? さきほどのモデルを今作った.stanファイルにそのまま貼り付 けてみる。 ? ハイライト(色づけ)されるようになった。 ? 少し打つと、予約語が自動的に出てくるようになった。 【推奨】RコードとStanコードを別々に記述するには?
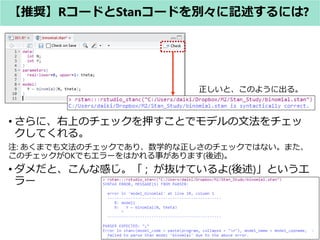
- 32. ? さらに、右上のチェックを押すことでモデルの文法をチェッ クしてくれる。 注: あくまでも文法のチェックであり、数学的な正しさのチェックではない。また、 このチェックがOKでもエラーをはかれる事があります(後述)。 ? ダメだと、こんな感じ。「 ; が抜けているよ(後述)」というエ ラー 【推奨】RコードとStanコードを別々に記述するには? 正しいと、このように出る。
- 33. library("rstan") N <- 10 Y <- 8 dat <- list(N=N, Y=Y) fit <- stan(file = "binomial.stan", data = dat, iter = 1000, warmup = 500, chains = 3, seed = 1234, thin = 1) fit stan_dens(fit) # 事後分布可視化 ? 今書いたコードを実行す るには、先ほどのコード を右のように変更する。 (.stanファイルを作成した ため、モデルの部分がカッ トされた。) ? このコードを実行するた めには、作業ディレクト リを.stanファイルのある フォルダに設定して実行 してください。 【推奨】RコードとStanコードを別々に記述するには?
- 34. N <- 10 Y <- 8 dat <- list(N=N, Y=Y) ? 次は、データにあたる部分。 ? 今回は、コインを10回投げたら(N=10)、8回表が出た(Y=8)。 ? 分析用データとして、datをリスト形式で用意してあげる。 (pystanの場合、pythonでは辞書型で与えてあげる) ? リストの中には、モデルのdata{}で囲んだ部分に書いたものと全く同じも のを入れる必要がある(大文字小文字、型等も揃える)。 話を戻して、ここまでのコードを読み解く そのため、今回は、NとYをデータとして与える 必要がある。 また、下記のように与えても問題ない dat <- list(N=10, Y=8)
- 35. fit <- stan(file = "binomial.stan", data = dat, iter = 1000, warmup = 500, chains = 3, seed = 1234, thin = 1) 次は、実際の推定部分 ? file= どの.stanファイルを使うのか指定(ワーキングディレクトリ内) ? data= 分析データ ? iter= 何回乱数生成計算(MCMC)を行うか ( デフォルト=2000) ? warmup= iterのうち何回を初期値依存として、結果に反映させないか (warmup<iter) (デフォ= iter/2) ? chain= 何本の乱数列で計算を行うか? (デフォ=4) ? seed= 初期値をいくつから始めるかのシード値 ? thin= 結果をいくつずつ間引いて使うか (デフォ=1) ここまでのコードを読み解く
- 36. fit stan_dens(fit) # 事後分布可視化 ? 今回、fitは結果を表示 ? stan_dens()は、事後分布を表示する関数。各パラメータの事 後確率をカーネル密度推定し(なめらかに線を引いて) 、事後 分布をプロットする関数。 ここまでのコードを読み解く
- 37. ? パッケージ読み込んで~ ? データ作成(指定)して~ ? データをリスト型で集 約して~ ? Stanに渡して、MCMC~ ? 結果表示して~ ? 事後分布見てみる。 無事、ここまでのコードを読み解けたでしょうか? library("rstan") N <- 10 Y <- 8 dat <- list(N=N, Y=Y) fit <- stan(file = "binomial.stan", data = dat, iter = 1000, warmup = 500, chains = 3, seed = 1234, thin = 1) fit stan_dens(fit) # 事後分布可視化
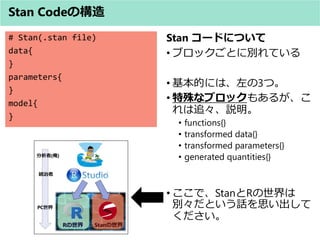
- 38. Stan コードについて ? ブロックごとに別れている ? 基本的には、左の3つ。 ? 特殊なブロックもあるが、こ れは追々、説明。 ? functions{} ? transformed data{} ? transformed parameters{} ? generated quantities{} ? ここで、StanとRの世界は 別々だという話を思い出して ください。 Stan Codeの构造 # Stan(.stan file) data{ } parameters{ } model{ }
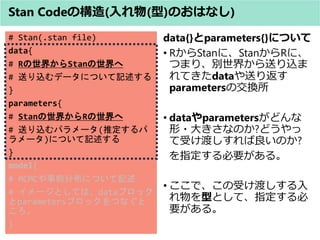
- 39. Stan コードについて ? それぞれの役割とイメージ data{ # RからStanへ } parameters{ # StanからRへ } model{ # 事前分布&MCMC~? } Stan Codeの构造 # Stan(.stan file) data{ # Rの世界からStanの世界へ # 送り込むデータについて記述する } parameters{ # Stanの世界からRの世界へ # 送り込むパラメータ(推定するパ ラメータ)について記述する } model{ # MCMCや事前分布について記述 # イメージとしては、dataブロック とparametersブロックをつなぐと ころ。 }
- 40. # Stan(.stan file) data{ # Rの世界からStanの世界へ # 送り込むデータについて記述する } parameters{ # Stanの世界からRの世界へ # 送り込むパラメータ(推定するパ ラメータ)について記述する } model{ # MCMCや事前分布について記述 # イメージとしては、dataブロック とparametersブロックをつなぐと ころ。 } data{}とparameters{}について ? RからStanに、StanからRに、 つまり、別世界から送り込ま れてきたdataや送り返す parametersの交換所 ? dataやparametersがどんな 形?大きさなのか?どうやっ て受け渡しすれば良いのか? を指定する必要がある。 ? ここで、この受け渡しする入 れ物を型として、指定する必 要がある。 Stan Codeの构造(入れ物(型)のおはなし)
- 41. Stan Codeの构造(入れ物(型)のおはなし) ? 型の種類(アヒル本 表9.1.a 引用) 何の型? 例 説明 整数 int N 整数を表す変数 実数 real Y 実数を表す変数 整数の配列 int Y[N] N個の整数を要素とする配列 実数の配列 real Y[N, M, L] N×M×L個の実数を要素とする配列 整数or実数 (戸建て) イメージ 整数の配列or実数の配列 (複数の戸建て)
- 42. Stan Codeの构造(入れ物(型)のおはなし) ? 型の種類(アヒル本 表9.1.bより引用) 何の型? 例 説明 ベクトル vector[K] V 1個の「長さKのベクトル」 ベクトルの配列 vector[K] V[N] N個の「長さKのベクトル」 ベクトルの配列 vector[K] V[N,M] N×M個の「長さKのベクトル」 行列 matrix[J,K] X 1個の「J行K列の行列」 行列の配列 matrix[J,K] X[N] N個の「J行K列の行列」 整数or実数 (スカラー) イメージ ベクトルの配列 (複数の複数階の戸建て) ベクトル (複数階の戸建て) 行列 (マンション) J行 K列 N個 長さK 長さK長さK
- 43. Stan Codeの构造(入れ物(型)のおはなし) ? 実際の使用例 ? 行ベクトル/列ベクトル 例 説明 int<lower=0> N 0以上を満たす整数を表す変数 real<upper=3> Y 3以下を満たす実数を表す変数 int<lower=0, upper=3> Y 0以上3以下を満たす整数を表す変数 列ベクトル行列 行 列 301,302,303 行ベクトル (列)ベクトル vector[K] V 1個の「長さKの列ベクトル」 行ベクトル row_vector[K] V 1個の「長さKの行ベクトル」 102, 202, 302, 402号室
- 44. Stan Codeの构造(入れ物(型)のおはなし) ? Stan内蔵の特別なベクトルの型 例 説明 simplex[K] theta K個の要素すべてが[0,1]の範囲を満たし、 合計が1の列ベクトル unit_vector[K] X K個の要素の二乗の合計が1の列ベクトル ordered[K] X K個の要素が順序制約を満たす列ベクトル ?1 < ?2 < ?3 < ? < ? ? positive_ordered[K] X K個の正の要素が順序制約を満たす列ベクトル 0 < ?1 < ?2 < ?3 < ? < ? ?
- 45. Stan Codeの构造(入れ物(型)のおはなし) ? Stan内蔵の特別な行列の型 例 説明 cov_matrix[D] cov D次元の分散共分散行列(対称行列?半正定値) corr_matrix[D] cor D次元の相関行列(対称行列?半正定値?対角成分が1) cholesky_factor_cov[D] CFCv D次元の分散共分散行列のコレスキー因子 (下三角行列?対角成分が正) cholesky_factor_corr[D] CFCr D次元の相関行列のコレスキー因子 (下三角行列?対角成分が正?各行で要素の二乗和が1)
- 46. Stan Codeの构造(入れ物(型)のおはなし) ? アクセスの仕方(matrix[J,K] X と宣言した場合) アクセス例 説明 X[j] or X[j, ] or X[j, : ] j行目の行ベクトル(要素はK個) X[1,k] 1行k列の要素 X[1:2, 1:2] 2行2列の部分行列 行 列 X[j] or X[j, ] or X[j, : ] X[1,k] X[1:2, 1:2] アクセスのイメージ j 行 列 k 1 行 列 1 2 1 2
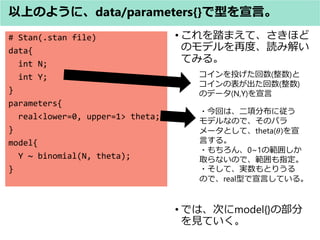
- 47. 以上のように、data/parameters{}で型を宣言。 ? これを踏まえて、さきほど のモデルを再度、読み解い てみる。 ? では、次にmodel{}の部分 を見ていく。 # Stan(.stan file) data{ int N; int Y; } parameters{ real<lower=0, upper=1> theta; } model{ Y ~ binomial(N, theta); } コインを投げた回数(整数)と コインの表が出た回数(整数) のデータ(N,Y)を宣言 ?今回は、二項分布に従う モデルなので、そのパラ メータとして、theta(?)を宣 言する。 ?もちろん、0~1の範囲しか 取らないので、範囲も指定。 ?そして、実数もとりうる ので、real型で宣言している。
- 48. Stan コードについて ? それぞれの役割とイメージ data{ # RからStanへ } parameters{ # StanからRへ } model{ # 事前分布&MCMC~? } 【再掲】Stan Codeの构造 # Stan(.stan file) data{ # Rの世界からStanの世界へ # 送り込むデータについて記述する } parameters{ # Stanの世界からRの世界へ # 送り込むパラメータ(推定するパ ラメータ)について記述する } model{ # MCMCや事前分布について記述 # イメージとしては、dataブロック とparametersブロックをつなぐと ころ。 }
- 49. # Stan(.stan file) data{ # Rの世界からStanの世界へ # 送り込むデータについて記述する } parameters{ # Stanの世界からRの世界へ # 送り込むパラメータ(推定するパ ラメータ)について記述する } model{ # MCMCや事前分布について記述 # イメージとしては、dataブロック とparametersブロックをつなぐと ころ。 } model{}について ? これまで用意してきたdataや parameterを使って、事後分 布を導き出す。 ? 事前分布や尤度については、 ここで記述する。 ? つまり、~(サンプリング)は、 このブロックでしか行えない。 Stan Codeの构造(model{}のおはなし)
- 50. # Stan(.stan file) data{ int N; int Y; } parameters{ real<lower=0,upper=1> theta; } model{ Y ~ binomial(N, theta); } 今回のモデル ? 10回(N)コインを投げて、8回 (Y)表が出る確率θを推定した い。 ? このとき、θは二項分布 (binomial)に従う。 ? 左のように記述する。 Stan Codeの构造(model{}のおはなし) model{} でMCMCを行っている
- 51. # Stan(.stan file) data{ int N; int Y; } parameters{ real<lower=0,upper=1> theta; } model{ Y ~ binomial(N, theta); } 今回のモデル ? 10回(N)コインを投げて、8回 (Y)表が出る確率θを推定した い。 ? このとき、θは二項分布 (binomial)に従う。 ? 左のように記述する。 Stan Codeの构造(model{}のおはなし) model{} は計算(MCMC等)のための要
- 53. Markov Chain Monte Calro (マルコフ連鎖モンテカルロ法) ? Stanで、事後確率を求めるために行われている計算の一つ ? MCMCの種類(一部のみ紹介) ? Gibbs sampling(ギブスサンプリング) ? Metropolis algorithm (メトロポリス法) ? Hamiltonian Monte Carlo(ハミルトニアンモンテカルロ(HMC)法) ? No-U-Turns Sampler(NUTSアルゴリズム) ? Stanに導入されているアルゴリズム ? HMC法によるNUTSアルゴリズム ? ADVI(automatic differentiation variational inference; 自動変分ベイズ) どれがどう違うのか?
- 57. MCMC法は最強なのか? ? あくまでも近似である。 ? 故に、確率が収束しているのか検討する必要がある。 ? また、綺麗に乱数を生成できているのか調べる必要がある。 ? 収束を確認する ? Gelman-Rubin収束判定 ? 目視による確認(トレースプロット) ? 乱数生成に問題ないか? ? 自己相関のチェック ? 実行サンプルサイズのチェック 等々 これらの基準をクリアして、事後平均だったり事後分布を見ることに 意味がある
- 58. 実践ベイズモデリング
- 59. ベイズモデリングのために必要なこと ? 記述統計?散布図?ヒストグラムを書く ? 簡単なモデル(既存のモデル)から考えていく。 例 ? 単回帰分析 ? 重回帰分析 ? 階層モデル ? 自分書いたモデルを眺めまくる ? 仮定をおかないということは”仮定をおかない仮定を置くこと” ? 気付かないうちに仮定を置いていることも??? ? 無情報は”無情報という有情報”を与えている。 ? モデルを何度も壊して、変えて、直して、作って??? ? 事前分布を変えてみる ? いろんなモデル同士を比較してみる
- 60. ベイズモデリングのために必要なこと ? そして、想像力 ? 既存の分析モデルでできなかったことができるのがベイズ統計モデリン グの良いところです。 ? 収束さえしてしまえば、どんなモデルであっても問題ありません。ただ、 そのモデルから出てきたものが何を表しているのか検討する必要がある。 ? どういう仮定をおいたもとででてきたものなのか? ? この正当性が客観的に担保できたうえで、どんなすごいモデルを作れるか? さぁ、今こそベイズモデラーになりましょう







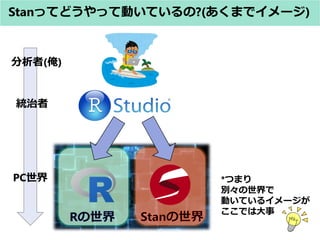
















![Stan Codeの构造(入れ物(型)のおはなし)
? 型の種類(アヒル本 表9.1.a 引用)
何の型? 例 説明
整数 int N 整数を表す変数
実数 real Y 実数を表す変数
整数の配列 int Y[N] N個の整数を要素とする配列
実数の配列 real Y[N, M, L] N×M×L個の実数を要素とする配列
整数or実数
(戸建て)
イメージ
整数の配列or実数の配列
(複数の戸建て)](https://image.slidesharecdn.com/stan0731-170731145356/85/Stan-41-320.jpg)
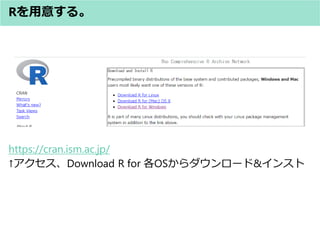
![Stan Codeの构造(入れ物(型)のおはなし)
? 型の種類(アヒル本 表9.1.bより引用)
何の型? 例 説明
ベクトル vector[K] V 1個の「長さKのベクトル」
ベクトルの配列 vector[K] V[N] N個の「長さKのベクトル」
ベクトルの配列 vector[K] V[N,M] N×M個の「長さKのベクトル」
行列 matrix[J,K] X 1個の「J行K列の行列」
行列の配列 matrix[J,K] X[N] N個の「J行K列の行列」
整数or実数
(スカラー)
イメージ
ベクトルの配列
(複数の複数階の戸建て)
ベクトル
(複数階の戸建て)
行列
(マンション)
J行
K列
N個
長さK 長さK長さK](https://image.slidesharecdn.com/stan0731-170731145356/85/Stan-42-320.jpg)
![Stan Codeの构造(入れ物(型)のおはなし)
? 実際の使用例
? 行ベクトル/列ベクトル
例 説明
int<lower=0> N 0以上を満たす整数を表す変数
real<upper=3> Y 3以下を満たす実数を表す変数
int<lower=0, upper=3> Y 0以上3以下を満たす整数を表す変数
列ベクトル行列
行
列
301,302,303
行ベクトル
(列)ベクトル vector[K] V 1個の「長さKの列ベクトル」
行ベクトル row_vector[K] V 1個の「長さKの行ベクトル」
102,
202,
302,
402号室](https://image.slidesharecdn.com/stan0731-170731145356/85/Stan-43-320.jpg)
![Stan Codeの构造(入れ物(型)のおはなし)
? Stan内蔵の特別なベクトルの型
例 説明
simplex[K] theta K個の要素すべてが[0,1]の範囲を満たし、
合計が1の列ベクトル
unit_vector[K] X K個の要素の二乗の合計が1の列ベクトル
ordered[K] X K個の要素が順序制約を満たす列ベクトル
?1 < ?2 < ?3 < ? < ? ?
positive_ordered[K] X K個の正の要素が順序制約を満たす列ベクトル
0 < ?1 < ?2 < ?3 < ? < ? ?](https://image.slidesharecdn.com/stan0731-170731145356/85/Stan-44-320.jpg)
![Stan Codeの构造(入れ物(型)のおはなし)
? Stan内蔵の特別な行列の型
例 説明
cov_matrix[D] cov D次元の分散共分散行列(対称行列?半正定値)
corr_matrix[D] cor D次元の相関行列(対称行列?半正定値?対角成分が1)
cholesky_factor_cov[D] CFCv D次元の分散共分散行列のコレスキー因子
(下三角行列?対角成分が正)
cholesky_factor_corr[D] CFCr D次元の相関行列のコレスキー因子
(下三角行列?対角成分が正?各行で要素の二乗和が1)](https://image.slidesharecdn.com/stan0731-170731145356/85/Stan-45-320.jpg)
![Stan Codeの构造(入れ物(型)のおはなし)
? アクセスの仕方(matrix[J,K] X と宣言した場合)
アクセス例 説明
X[j] or X[j, ] or X[j, : ] j行目の行ベクトル(要素はK個)
X[1,k] 1行k列の要素
X[1:2, 1:2] 2行2列の部分行列
行
列
X[j] or X[j, ] or X[j, : ] X[1,k] X[1:2, 1:2]
アクセスのイメージ
j
行
列
k
1
行
列
1
2
1 2](https://image.slidesharecdn.com/stan0731-170731145356/85/Stan-46-320.jpg)