Sorting
Download as PPTX, PDF0 likes1,635 views
Salahsatu submateri perkuliahan Algoritma Dasar
![Bubble Sort: pseudocode
BUBBLESORT(A)
1 for i1 to length[A]
2
for jlength[A] downto i+1
3
if A[j] < A[j-1]
4
then exchange A[j] A[j-1]](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-3-320.jpg)
![Selection Sort: Pseudocode
SELECTIONSORT(A)
1 for i 1 to length[A]-1
2
min = i;
3
for j i+1 to length[A]
4
if A[j] < A[min]
5
min = j;
6
exchange A[min] A[i]
Prinsip kerja:
Dari elemen sebanyak n,
Carilah elemen terkecil dari array A, dan swap-lah elemen terkecil
tersebut dengan elemen pertama (A[1] ).
Carilah elemen terkecil kedua dari array A, dan swap-lah elemen
tersebut dengan elemen kedua (A[2])
Ulangi sampai n-1 elemen pertama dari array A](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-20-320.jpg)
![Insertion Sort: pseudocode
INSERTION-SORT(A)
1
for j2 to length[A]
2
do keyA[j]
3
Insert A[j] ke sekuens yang sudah disorting A[1j-1]
4
i j-1
5
while i>0 and A[i] > key
6
do A[i+1] A[i]
7
i i -1
8
A[i+1] key](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-23-320.jpg)
![Merge Sort: pseudocode
MERGE (A, p,q,r)
1
n1q-p+1
2
n2r-q
3
create arrays L[1..n1+1] and R[1..n2+1]
4
for i 1 to n1
5
do L[i] A[p+i-1]
6
for j 1 to n2
7
do R[j] A[q+j ]
8
L[n1+1]
9
R[n2+1]
10
i 1
11
j 1
12
for k p to r
13
do if L[i] < R[j]
14
then A[k] L[i]
15
i i+1
16
else A[k] R[j]
17
j j+1](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-27-320.jpg)
![Prinsip Kerja Quick Sort
Divide
Partisilah array A[pr] ke dalam dua buah subarray A[pq-1] dan
A[q+1r] sedemikian hingga
tiap elemen pada A[pq-1] senantiasa lebih kecil atau sama
dengan A[q] DAN
tiap elemen pada A[q+1r] senantiasa sama atau lebih besar
dari A[q]
Hitunglah q
Conquer
Urutkan (sorting-lah) A[pq-1] dan A[q+1r] secara rekursif
Combine
Kedua subarray telah diurutkan pada posisi masing-masing,
sehingga tidak diperlukan upaya khusus untuk mengkombinasikan
mereka. A[pr] telah ter-sorting](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-32-320.jpg)
![Quick Sort: pseudocode
QUICKSORT (A, p,r)
1
If p<r
2
then qPARTITION (A,p,r)
3
QUICKSORT(A,p,q-1)
4
QUICKSORT(A,q+1,r)
PARTITION(A, p,r)
1
xA[r]
2
ip-1
3
for jp to r-1
4 do if A[j] < x
5
then ii+1
6
exchange A[i] A[j]
7
exchange A[i+1] A[r]
8
return i+1
1. Tetapkan data paling kanan sebagai
pivot
2. Pindahkan semua data yang lebih
kecil daripada pivot ke sayap kiri
3. Pindahkan semua data yang lebih
besar daripada pivot ke sayap kanan
4. Pivot urutan ke berapa ?](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-33-320.jpg)
![Quick Sort: Contoh
1
(a)
2
i
i=0
p=j=1
r=8
i=1
j=1
p=1
r=8
p,j
2
3
8
7
4
5
6
7
8
1
3
5
6
4
r
PARTITION(A, p,r)
1
xA[r] x=4
2
ip-1
i=0
3
for jp to r-1 j=1
4
do if A[j] < x
2 < 4 ? YES
5
then ii+1 i=1
6
exchange A[i] A[j] exchange 2 & 2
7
exchange A[i+1] A[r]
8
return i+1](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-35-320.jpg)
![Quick Sort: Contoh
1
(b)
i=1
j=1
p=1
r=8
i=1
j=2
p=1
r=8
2
3
2
8
p,i
7
4
5
6
7
8
1
3
5
6
4
j
PARTITION(A, p,r)
1
xA[r]
2
ip-1
3
for jp to r-1 j=2
4
do if A[j] < x
8 < 4 ? NO
5
then ii+1
6
exchange A[i] A[j]
7
exchange A[i+1] A[r]
8
return i+1
r](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-36-320.jpg)
![Quick Sort: Contoh
1
(c)
i=1
j=2
p=1
r=8
i=1
j=3
p=1
r=8
2
p,i
2
3
8
4
7
5
6
7
8
1
3
5
6
4
j
PARTITION(A, p,r)
1
xA[r]
2
ip-1
3
for jp to r-1 j=3
4
do if A[j] < x
7 < 4 ? NO
5
then ii+1
6
exchange A[i] A[j]
7
exchange A[i+1] A[r]
8
return i+1
r](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-37-320.jpg)
![Quick Sort: Contoh
1
(d)
i=1
j=3
p=1
r=8
i=2
j=4
p=1
r=8
2
2
3
8
p,i
4
6
7
8
1
7
5
3
5
6
4
j
2
1
p
i
r
7
8
j
3
5
6
4
r
PARTITION(A, p,r)
1
xA[r]
2
ip-1
3
for jp to r-1 j=4
4
do if A[j] < x
1 < 4 ? YES
i=2
5
then ii+1
6
exchange A[i] A[j] exchange 8 & 1
7
exchange A[i+1] A[r]
8
return i+1](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-38-320.jpg)
![Quick Sort: Contoh
1
(e)
i=2
j=4
p=1
r=8
i=3
j=5
p=1
r=8
2
3
4
5
6
7
8
2
1
7
8
3
5
6
4
2
1
3
8
7
5
6
4
p
i
j
r
PARTITION(A, p,r)
1
xA[r]
2
ip-1
3
for jp to r-1 j=5
4
do if A[j] < x
3 < 4 ? YES
5
then ii+1 i=3
6
exchange A[i] A[j] exchange 7 & 3
7
exchange A[i+1] A[r]
8
return i+1](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-39-320.jpg)
![Quick Sort: Contoh
1
(f)
i=3
j=5
p=1
r=8
i=3
j=6
p=1
r=8
2
p
2
3
1
4
3
i
5
6
7
8
8
7
5
6
4
j
PARTITION(A, p,r)
1
xA[r]
2
ip-1
3
for jp to r-1 j=6
4
do if A[j] < x
5 < 4 ? NO
5
then ii+1
6
exchange A[i] A[j]
7
exchange A[i+1] A[r]
8
return i+1
r](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-40-320.jpg)
![Quick Sort: Contoh
1
(g)
i=3
j=6
p=1
r=8
i=3
j=7
p=1
r=8
2
p
2
3
1
4
3
i
5
6
7
8
8
7
5
6
4
j
r
PARTITION(A, p,r)
1
xA[r]
2
ip-1
3
for jp to r-1 j=7
4
do if A[j] < x
6 < 4 ? NO
5
then ii+1
6
exchange A[i] A[j]
7
exchange A[i+1] A[r]
8
return i+1](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-41-320.jpg)
![Quick Sort: Contoh
1
(h)
i=3
j=7
p=1
r=8
2
3
4
5
6
7
8
2
1
3
8
7
5
6
4
2
1
3
4
7
5
6
8
p
i
j
PARTITION(A, p,r)
1
xA[r]
2
ip-1
3
for jp to r-1
4
do if A[j] < x
5
then ii+1
6
exchange A[i] A[j]
7
exchange A[i+1] A[r] exchange 4 & 8
8
return i+1
return 4 (q=4)
r](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-42-320.jpg)
![Randomized Quicksort
RANDOMIZED-QUICKSORT (A, p,r)
1
If p<r
2
then qRANDOMIZED-PARTITION (A,p,r)
3
RANDOMIZED-QUICKSORT(A,p,q-1)
4
RANDOMIZED-QUICKSORT(A,q+1,r)
RANDOMIZED-PARTITION(A, p,r)
1 iRANDOM(p,r)
2 exchange A[r] A[i]
3 return PARTITION (A,p,r)](https://image.slidesharecdn.com/sorting-131016220429-phpapp01/85/Sorting-46-320.jpg)
More Related Content
What's hot (20)
More from Zezen Wahyudin (11)
Sorting
- 2. Beberapa Algoritma Sorting 1. 2. 3. 4. 5. Bubble Sort Selection Sort Insertion Sort Merge Sort Quick Sort
- 3. Bubble Sort: pseudocode BUBBLESORT(A) 1 for i1 to length[A] 2 for jlength[A] downto i+1 3 if A[j] < A[j-1] 4 then exchange A[j] A[j-1]
- 4. Contoh Algoritma: BUBBLE SORT banyaknya data: n Data diurutkan/disorting dari yang bernilai besar Proses step 1 : step 2 : : step n-1 Periksalah nilai dua elemen mulai dari urutan ke-n sampai urutan ke-1. Jika nilai kiri<kanan, tukarkan kedua data itu. Periksalah nilai dua elemen mulai dari urutan ke-n sampai urutan ke-2. Jika nilai kiri<kanan, tukarkan kedua data itu. Periksalah nilai dua elemen mulai dari urutan ke-n sampai urutan ke-n-1. Jika nilai kiri<kanan, tukarkan kedua data itu.
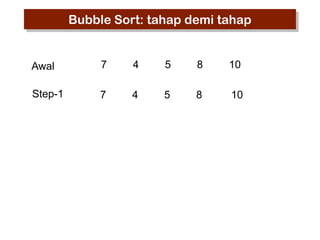
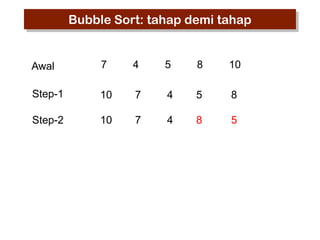
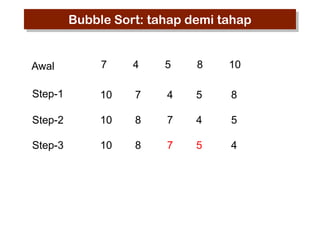
- 5. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10
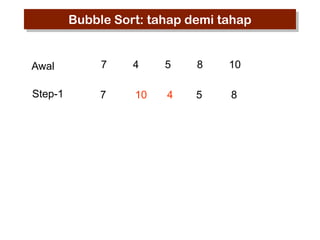
- 6. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 7 4 5 8 10
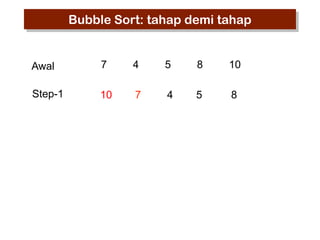
- 7. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 7 4 5 10 8
- 8. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 7 4 10 5 8
- 9. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 7 10 4 5 8
- 10. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 10 7 4 5 8
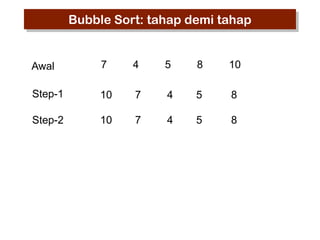
- 11. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 10 7 4 5 8 Step-2 10 7 4 5 8
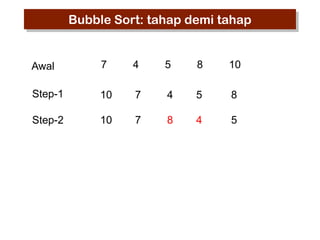
- 12. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 10 7 4 5 8 Step-2 10 7 4 8 5
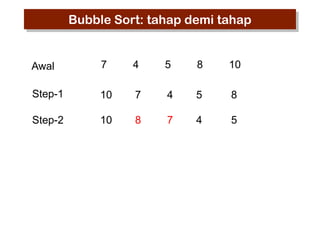
- 13. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 10 7 4 5 8 Step-2 10 7 8 4 5
- 14. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 10 7 4 5 8 Step-2 10 8 7 4 5
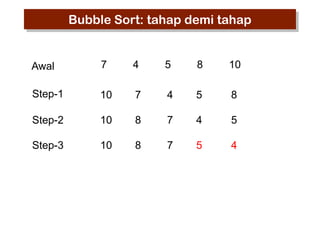
- 15. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 10 7 4 5 8 Step-2 10 8 7 4 5 Step-3 10 8 7 4 5
- 16. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 10 7 4 5 8 Step-2 10 8 7 4 5 Step-3 10 8 7 5 4
- 17. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 10 7 4 5 8 Step-2 10 8 7 4 5 Step-3 10 8 7 5 4
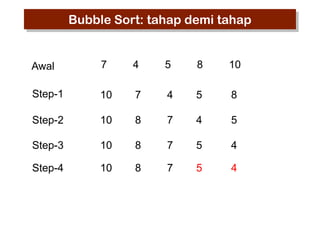
- 18. Bubble Sort: tahap demi tahap Awal 7 4 5 8 10 Step-1 10 7 4 5 8 Step-2 10 8 7 4 5 Step-3 10 8 7 5 4 Step-4 10 8 7 5 4
- 19. Beberapa Algoritma Sorting 1. 2. 3. 4. 5. Bubble Sort Selection Sort Insertion Sort Merge Sort Quick Sort
- 20. Selection Sort: Pseudocode SELECTIONSORT(A) 1 for i 1 to length[A]-1 2 min = i; 3 for j i+1 to length[A] 4 if A[j] < A[min] 5 min = j; 6 exchange A[min] A[i] Prinsip kerja: Dari elemen sebanyak n, Carilah elemen terkecil dari array A, dan swap-lah elemen terkecil tersebut dengan elemen pertama (A[1] ). Carilah elemen terkecil kedua dari array A, dan swap-lah elemen tersebut dengan elemen kedua (A[2]) Ulangi sampai n-1 elemen pertama dari array A
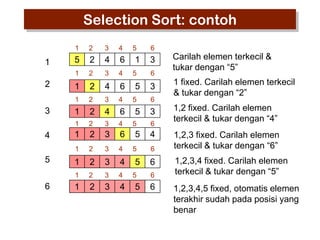
- 21. Selection Sort: contoh 1 6 4 6 2 3 4 1 2 4 6 2 3 4 1 2 4 6 2 3 4 1 2 3 6 2 3 4 1 2 3 4 1 5 2 1 4 5 1 3 4 1 2 3 1 1 2 2 3 4 1 2 3 4 5 1 5 5 5 5 5 5 5 5 5 5 6 3 6 3 6 3 6 4 6 6 6 6 Carilah elemen terkecil & tukar dengan 5 1 fixed. Carilah elemen terkecil & tukar dengan 2 1,2 fixed. Carilah elemen terkecil & tukar dengan 4 1,2,3 fixed. Carilah elemen terkecil & tukar dengan 6 1,2,3,4 fixed. Carilah elemen terkecil & tukar dengan 5 1,2,3,4,5 fixed, otomatis elemen terakhir sudah pada posisi yang benar
- 22. Beberapa Algoritma Sorting 1. 2. 3. 4. 5. Bubble Sort Selection Sort Insertion Sort Merge Sort Quick Sort
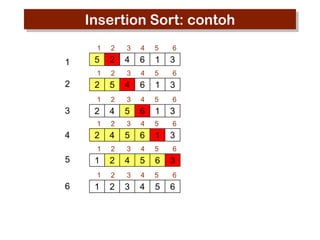
- 23. Insertion Sort: pseudocode INSERTION-SORT(A) 1 for j2 to length[A] 2 do keyA[j] 3 Insert A[j] ke sekuens yang sudah disorting A[1j-1] 4 i j-1 5 while i>0 and A[i] > key 6 do A[i+1] A[i] 7 i i -1 8 A[i+1] key
- 25. Quiz Diketahui deretan data sbb. 80 84 100 24 79 85 91 65 17 3 1 21 1. Urutkan data tsb. memakai Selection Sort, agar elemen terkecil berada paling depan (urutan pertama), semakin ke belakang semakin besar 2. Urutkan data tsb. memakai Selection Sort, agar elemen terbesar berada paling depan (urutan pertama), semakin ke belakang semakin kecil 3. Urutkan data tsb. memakai Insertion Sort, agar elemen terkecil berada paling depan (urutan pertama), semakin ke belakang semakin besar 4. Urutkan data tsb. memakai Insertion Sort, agar elemen terbesar berada paling depan (urutan pertama), semakin ke belakang semakin kecil
- 26. Beberapa Algoritma Sorting 1. 2. 3. 4. 5. Bubble Sort Selection Sort Insertion Sort Merge Sort Quick Sort
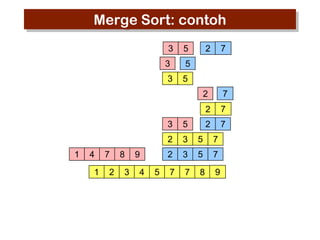
- 27. Merge Sort: pseudocode MERGE (A, p,q,r) 1 n1q-p+1 2 n2r-q 3 create arrays L[1..n1+1] and R[1..n2+1] 4 for i 1 to n1 5 do L[i] A[p+i-1] 6 for j 1 to n2 7 do R[j] A[q+j ] 8 L[n1+1] 9 R[n2+1] 10 i 1 11 j 1 12 for k p to r 13 do if L[i] < R[j] 14 then A[k] L[i] 15 i i+1 16 else A[k] R[j] 17 j j+1
- 28. Merge Sort: pseudocode MERGE-SORT (A, p, r) 1 If p<r 2 then q (p+r)/2 3 MERGE-SORT (A, p, q) 4 MERGE-SORT (A, q+1, r) 5 MERGE(A,p,q,r)
- 31. Beberapa Algoritma Sorting 1. 2. 3. 4. 5. Bubble Sort Selection Sort Insertion Sort Merge Sort Quick Sort
- 32. Prinsip Kerja Quick Sort Divide Partisilah array A[pr] ke dalam dua buah subarray A[pq-1] dan A[q+1r] sedemikian hingga tiap elemen pada A[pq-1] senantiasa lebih kecil atau sama dengan A[q] DAN tiap elemen pada A[q+1r] senantiasa sama atau lebih besar dari A[q] Hitunglah q Conquer Urutkan (sorting-lah) A[pq-1] dan A[q+1r] secara rekursif Combine Kedua subarray telah diurutkan pada posisi masing-masing, sehingga tidak diperlukan upaya khusus untuk mengkombinasikan mereka. A[pr] telah ter-sorting
- 33. Quick Sort: pseudocode QUICKSORT (A, p,r) 1 If p<r 2 then qPARTITION (A,p,r) 3 QUICKSORT(A,p,q-1) 4 QUICKSORT(A,q+1,r) PARTITION(A, p,r) 1 xA[r] 2 ip-1 3 for jp to r-1 4 do if A[j] < x 5 then ii+1 6 exchange A[i] A[j] 7 exchange A[i+1] A[r] 8 return i+1 1. Tetapkan data paling kanan sebagai pivot 2. Pindahkan semua data yang lebih kecil daripada pivot ke sayap kiri 3. Pindahkan semua data yang lebih besar daripada pivot ke sayap kanan 4. Pivot urutan ke berapa ?
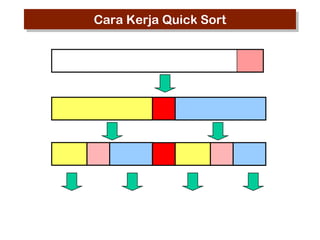
- 34. Cara Kerja Quick Sort
- 35. Quick Sort: Contoh 1 (a) 2 i i=0 p=j=1 r=8 i=1 j=1 p=1 r=8 p,j 2 3 8 7 4 5 6 7 8 1 3 5 6 4 r PARTITION(A, p,r) 1 xA[r] x=4 2 ip-1 i=0 3 for jp to r-1 j=1 4 do if A[j] < x 2 < 4 ? YES 5 then ii+1 i=1 6 exchange A[i] A[j] exchange 2 & 2 7 exchange A[i+1] A[r] 8 return i+1
- 36. Quick Sort: Contoh 1 (b) i=1 j=1 p=1 r=8 i=1 j=2 p=1 r=8 2 3 2 8 p,i 7 4 5 6 7 8 1 3 5 6 4 j PARTITION(A, p,r) 1 xA[r] 2 ip-1 3 for jp to r-1 j=2 4 do if A[j] < x 8 < 4 ? NO 5 then ii+1 6 exchange A[i] A[j] 7 exchange A[i+1] A[r] 8 return i+1 r
- 37. Quick Sort: Contoh 1 (c) i=1 j=2 p=1 r=8 i=1 j=3 p=1 r=8 2 p,i 2 3 8 4 7 5 6 7 8 1 3 5 6 4 j PARTITION(A, p,r) 1 xA[r] 2 ip-1 3 for jp to r-1 j=3 4 do if A[j] < x 7 < 4 ? NO 5 then ii+1 6 exchange A[i] A[j] 7 exchange A[i+1] A[r] 8 return i+1 r
- 38. Quick Sort: Contoh 1 (d) i=1 j=3 p=1 r=8 i=2 j=4 p=1 r=8 2 2 3 8 p,i 4 6 7 8 1 7 5 3 5 6 4 j 2 1 p i r 7 8 j 3 5 6 4 r PARTITION(A, p,r) 1 xA[r] 2 ip-1 3 for jp to r-1 j=4 4 do if A[j] < x 1 < 4 ? YES i=2 5 then ii+1 6 exchange A[i] A[j] exchange 8 & 1 7 exchange A[i+1] A[r] 8 return i+1
- 39. Quick Sort: Contoh 1 (e) i=2 j=4 p=1 r=8 i=3 j=5 p=1 r=8 2 3 4 5 6 7 8 2 1 7 8 3 5 6 4 2 1 3 8 7 5 6 4 p i j r PARTITION(A, p,r) 1 xA[r] 2 ip-1 3 for jp to r-1 j=5 4 do if A[j] < x 3 < 4 ? YES 5 then ii+1 i=3 6 exchange A[i] A[j] exchange 7 & 3 7 exchange A[i+1] A[r] 8 return i+1
- 40. Quick Sort: Contoh 1 (f) i=3 j=5 p=1 r=8 i=3 j=6 p=1 r=8 2 p 2 3 1 4 3 i 5 6 7 8 8 7 5 6 4 j PARTITION(A, p,r) 1 xA[r] 2 ip-1 3 for jp to r-1 j=6 4 do if A[j] < x 5 < 4 ? NO 5 then ii+1 6 exchange A[i] A[j] 7 exchange A[i+1] A[r] 8 return i+1 r
- 41. Quick Sort: Contoh 1 (g) i=3 j=6 p=1 r=8 i=3 j=7 p=1 r=8 2 p 2 3 1 4 3 i 5 6 7 8 8 7 5 6 4 j r PARTITION(A, p,r) 1 xA[r] 2 ip-1 3 for jp to r-1 j=7 4 do if A[j] < x 6 < 4 ? NO 5 then ii+1 6 exchange A[i] A[j] 7 exchange A[i+1] A[r] 8 return i+1
- 42. Quick Sort: Contoh 1 (h) i=3 j=7 p=1 r=8 2 3 4 5 6 7 8 2 1 3 8 7 5 6 4 2 1 3 4 7 5 6 8 p i j PARTITION(A, p,r) 1 xA[r] 2 ip-1 3 for jp to r-1 4 do if A[j] < x 5 then ii+1 6 exchange A[i] A[j] 7 exchange A[i+1] A[r] exchange 4 & 8 8 return i+1 return 4 (q=4) r
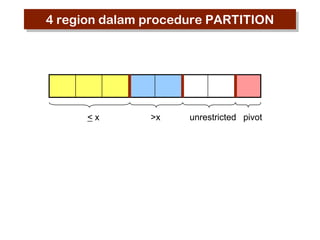
- 43. 4 region dalam procedure PARTITION <x >x unrestricted pivot
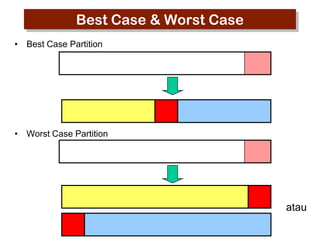
- 44. Best Case & Worst Case Best Case Partition Worst Case Partition atau
- 45. Quiz Diketahui deretan data sbb. 80 84 100 24 79 85 91 65 17 3 1 21 1. Urutkan data tsb. memakai Merge sort, agar elemen terkecil berada paling depan (urutan pertama), semakin ke belakang semakin besar 2. Urutkan data tsb. memakai Merge Sort, agar elemen terbesar berada paling depan (urutan pertama), semakin ke belakang semakin kecil 3. Urutkan data tsb. memakai Quick Sort, agar elemen terkecil berada paling depan (urutan pertama), semakin ke belakang semakin besar 4. Urutkan data tsb. memakai Quick Sort, agar elemen terbesar berada paling depan (urutan pertama), semakin ke belakang semakin kecil
- 46. Randomized Quicksort RANDOMIZED-QUICKSORT (A, p,r) 1 If p<r 2 then qRANDOMIZED-PARTITION (A,p,r) 3 RANDOMIZED-QUICKSORT(A,p,q-1) 4 RANDOMIZED-QUICKSORT(A,q+1,r) RANDOMIZED-PARTITION(A, p,r) 1 iRANDOM(p,r) 2 exchange A[r] A[i] 3 return PARTITION (A,p,r)