确率的深层学习における中间层の改良と高性能学习法の提案
- 1. 確率的深層学習における 中間層の改良と高性能学習法の提案 山形大学大学院理工学研究科 情報科学専攻 安田研究室 修士 2 年 勝亦 利宗 修士学位論文公聴会
- 2. 2 統計的機械学習理論 統計的機械学習の目標 : 生成モデルの再現 生成モデル データ 生成 推定 学習 学習モデル 汎 化 誤 差 汎化誤差が高くなると 未知のデータにはうまく判断できない ( 過学習 ) データが生成モデルから 生成されていると考える 汎化誤差を低減した学習法の発見 研究目標 人工知能を実現させる技術 : 機械学習 その中には確率モデルを使う分野 , 統計的機械学習がある
- 3. 3 研究の概観 2 つのモデルに対して 異なるアプローチから汎化能力の向上を目指す 1. 制限ボルツマンマシン分類器 [1,2] モデルの拡張 中間層のスパース正則化 [3] 2. 深層ボルツマンマシン [4] 空間モンテカルロ法 [5,6] を使った学習法 [7] 学習アルゴリズムの改善 1 : [H. Larochelle & Y. Bengio, 2008] 2 : [H. Larochelle et al., 2012] 3 : [ 勝亦利宗 , 安田宗樹 , 2020] 4 : [R. Salakhutdinov & G. Hinton, 2009] 5 : [M. Yasuda, 2015] 6 : [M. Yasuda & K. Uchizawa, 2020] 7 : [T. Katsumara & M. Yasuda, 2020]
- 5. 5 制限ボルツマンマシン分類器 Discriminative Restricted Boltzmann Machine (DRBM)[1,2,3] 出力層 中間層 入力層 DRBM の確率分布関数 1 : [H. Larochelle & Y . Bengio, Proceedings of the 25th international conference on Machine learning, 2008] 2 : [H. Larochelle, M. Mandel, R. Pascanu, & Y . Bengio, The Journal of Machine Learning Research, 2012] 3: [Y . Yokoyama, T. Katsumata, & M. Yasuda, The Review of Socionetwork Strategies, 2019] m が大きい 過学習は強くなる 中間素子の数 m が モデルの表現能力を決める
- 6. 6 スパース性を持つ中間層 自動的に中間素子を減らす仕組みを加えたい hj = 0 のとき… 不要な素子の値が 0 になりやすくなる仕組みがあれば 素子の数を制御できそうだ ! 中間素子の存在は モデルから消える ! 中間素子の数 m が多い 過学習は強くなる
- 7. 7 スパース性を持つ中間層 ( 提案モデル ) スパース正則化項 スパース正則化 DRBM(Sparse-DRBM; SDRBM) γj の最適な値は尤度関数の最大化によって求めることができる スパース項の働きで h は 0 を取りやすくなる h 確率密度 突出 モデルは自動的に不要な素子を削減できる ! [ 勝亦 , 安田 , 情報処理学会第82回全国大会 , 2020] 従来法 提案法 γj が大きい hj =0 の確率が高くなる →
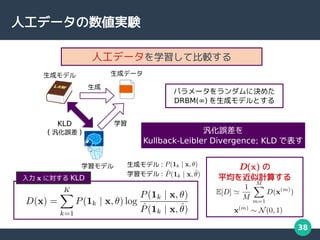
- 8. 8 人工データでの数値実験 提案モデルの 汎化能力は向上している 全体的に汎化誤差は低下 [ 勝亦 , 安田 , 情報処理学会第 82 回全国大会 , 2020] 汎化誤差 (KLD) 汎化誤差を Kullback-Leibler Divergence (KLD) で表す 生成 KLD ( 汎化誤差 ) 学習 事前に決めた パラメータ
- 9. 9 実データでの数値実験 実データを学習して比較する 訓練誤差 … 学習データに対する不正解率 テスト誤差 … テストデータに対する不正解率 テスト誤差 訓練誤差 テストデータ 学習モデル 学習データ 過学習 テスト誤差 訓練誤差 テストデータ 学習モデル 学習データ 過学習の改善 減 増
- 10. 10 数値実験 (MNIST) 訓練誤差 … 増加 テスト誤差 … 減少 down up [ 勝亦 , 安田 , 情報処理学会第 82 回全国大会 , 2020] 比較対象に Energy function constraint SDRBM(ESDRBM)[1] を使った ( 提案法よりも単純なスパース法 ) 1:[J.Wei, J.Lv & Z.Yi, International Journal of Pattern Recognition and Artificial Intelligence, 2019] MNIST と呼ばれる 手書き数字画像 データセット 学習データ 汎化能力は 向上していると言える Fashion-MNIST や CIFAR-10 などの データセットでも 同様の結果が得られた
- 11. 11 ここまでのまとめ – DRBM の中間素子にスパース性を持たせたモデルを提案した ● 数値実験によって汎化能力の向上を確認した 中間層が 1 つのモデルで スパース正則化を行った ここまでの研究 多層の中間層を持つモデルで スパース正則化を行いたい 次の目標 中間層を多層にするとモデルの表現能力は向上する
- 13. 13 Deep Boltzmann Machine[1] (DBM) 隠れ層 : 確率変数の層 可視層 : データを入力する層 L は隠れ層の数 , Hr は r 番目の隠れ層の素子数 1 : [R. Salakhutdinov & G. Hinton, Artificial intelligence and statistics, 2009] DBM の確率関数
- 14. 14 研究の流れ 隠れ層のスパース正則化 学習アルゴリズムの改善 – 従来法は学習精度が高くない – スパース化に不便 ここまで終了 スパース正則化の前に 学習アルゴリズムの改善が必要 今後の課題
- 15. 15 DBM の学習 DBM の学習は勾配法による対数尤度の最大化で行う 1 : [R. Salakhutdinov & G. Hinton, Artificial intelligence and statistics, 2009] 2 : [T. Katsumata & M. Yasuda, Nonlinear Theory and Its Applications (NOLTA 2020), 2020] DBM の勾配式 可視層を データで固定した モデルの期待値 可視層を データで固定しない モデルの期待値 : データ点 : 厳密和 = - 平均場近似法 モンテカルロ積分法 従来法 [1] 空間モンテカルロ積分法 提案法 [2] 勾配法は勾配の値を逐次的に加算する方法 厳密和の計算には指数時間の計算量が必要 ( 勾配 )
- 16. 16 提案アルゴリズムによる学習結果 1:[T. Katsumata & M.Yasuda, Proceedings of the 2020 International Symposium on Nonlinear Theory and Its Applications (NOLTA 2020), pp.29-32, 2020] 2:[T. Katsumata & M.Yasuda, Nonlinear Theory and Its Applications (NOLTA 2020), IEICE, 2020] 【投稿中】 down up up down 3 層の結果 [1] 両方の指標ともに従来法よりも 良い結果が得られている 生成 KLD ( 良い→低い ) 対数尤度 ( 良い→高い ) 事前に決めた パラメータ 4 層の結果 [2]
- 17. 17 まとめ ● 提案アルゴリズムを元に , スパース正則化 DBM の学習アルゴリズムの構築を行う 今後の課題 スパース正則化 制限ボルツマンマシン分類器 空間モンテカルロ積分法を用いた 深層ボルツマンマシンの学習 両方の手法ともに従来法よりも良い結果が得られた ! 汎化能力を向上させる 2 つの学習アルゴリズムを提案した
- 18. 18 研究実績 ● Y . Yokoyama, T. Katsumata, & M. Yasuda, “Restricted Boltzmann Machine with Multivalued Hidden Variables: a model suppressing over-fitting”, The Review of Socionetwork Strategies, Vol.13, no.2, pp.253- 266, 2019. ● T. Katsumata & M.Yasuda, “Effective Fine-Tuning Training of Deep Boltzmann Machine Based on Spatial Monte Carlo Integration”, Nonlinear Theory and Its Applications (NOLTA 2020), IEICE, 2020 【投稿中】 . 国内学会 ( 査読なし ) ● 勝亦利宗 , 安田宗樹 ,” スパース中間層を持つ制限ボルツマンマシン分類器”,情報処理学会第 82 回全国大会 (2020 年 3 月 5 日,金沢工業大学 , 口頭発表 ) 【学生奨励賞】 . ● 勝亦利宗 , 安田宗樹 ,” 深層ボルツマンマシンにおける学習アルゴリズムの改良”,情報処理学会第 83 回全国 大会 (2021 年 3 月 18 日,大阪大学 , 口頭発表 ) 【発表予定】 . 国際学会 ( 査読あり ) ? T. Katsumata & M.Yasuda, “Effective Fine-Tuning Algorithm for Deep Boltzmann Machine”, Proceedings of the 2020 International Symposium on Nonlinear Theory and Its Applications (NOLTA 2020), pp.29-32, 2020 学術論文 ( 査読あり )
- 19. 19 Appendix
- 20. 20 その他実験結果
- 21. 21 スパース正則化パラメータの挙動を解析する スパース正則化項の追加によって汎化能力は向上する 数値実験の結果 スパース正則化項は 本当に期待通りの動作をしているのだろうか ? スパース正則化項が中間素子を抑制する度合いを確認する 期待通りの動作ならば… 素子数が増える分 , スパース項は余分な素子を消し 抑制度は大きくなる 抑制度 分布 抑制度 分子の値が大きい → 中間素子の値は 0 を取りやすくなる
- 22. 22 実験結果 中間素子の数が増えるにつれ 抑制度も全体的に増加している スパース正則化項は 余分な中間素子を 抑制している 右に移動 [ 勝亦 , 安田 , 情報処理学会第 82 回全国大会 , 2020]
- 23. 23 fashion-MNIST – 28x28pixel – 学習データ : 10,000, テストデータ : 60,000 – MNIST と同様に ● 学習データを 1,000 件とする ● ガウスノイズ N(0, 2502) を加算した後 0,1 正規化 T-shirt Trouser Pullover Dress Coat Shirt Sneaker Sandal Bag Ankle Boot
- 24. 24 数値実験 (Fashion-MNIST) 訓練誤差 … 増加 テスト誤差 … 減少 down up 比較対象に Energy function constraint SDRBM(ESDRBM)[1] を使った ( 提案法よりも単純なスパース法 ) 1:[J.Wei, J.Lv & Z.Yi, International Journal of Pattern Recognition and Artificial Intelligence, 2019] Fashion-MNIST 服や靴などの 画像の分類 学習データ 素子数は 100
- 25. 25 CIFAR-10 Canadian Institute for Advanced Research (CIFAR) – 32x32 pixel – 学習データ :50,000 テストデータ : 10,000 ● 学習データを 500 に減らして学習 – モノクロ画像に変換して学習 ship truck dog horse airplane automobile deer cat bird frog
- 26. 26 数値実験 (CIFAR-10) 汎化能力は 向上していると言える 訓練誤差 … 増加 テスト誤差 … 減少 down up 比較対象に Energy function constraint SDRBM(ESDRBM)[1] を使った ( 提案法よりも単純なスパース法 ) 1:[J.Wei, J.Lv & Z.Yi, International Journal of Pattern Recognition and Artificial Intelligence, 2019] CIFAR-10 動物や乗り物などの 画像の分類 学習データ 素子数は 200
- 27. 27 統計的機械学習
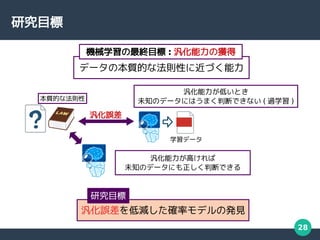
- 28. 28 研究目標 データの本質的な法則性に近づく能力 機械学習の最終目標 : 汎化能力の獲得 汎化誤差を低減した確率モデルの発見 研究目標 汎化能力が高ければ 未知のデータにも正しく判断できる 汎化誤差 汎化能力が低いとき 未知のデータにはうまく判断できない ( 過学習 ) 本質的な法則性 学習データ
- 29. 29 機械学習 機械学習とは ? – 人間が経験から学習するような仕組みを , 機械の上で実現させる技術 – 既に持っているデータを学習し , 知らないデータに対しても正しく判断できるようにしたい 統計的機械学習とは ? – 確率モデルを使った機械学習 – 観測データが未知なる確率法則に従って生成されていると 考え , その法則により近い学習モデルを得ることが目的 生成 推定 学習
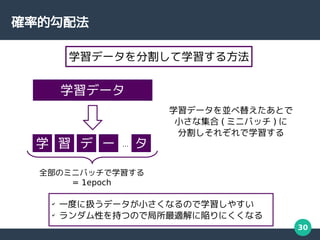
- 30. 30 確率的勾配法 学習データ 学 習 デ ー タ … 学習データを分割して学習する方法 学習データを並べ替えたあとで 小さな集合 ( ミニバッチ ) に 分割しそれぞれで学習する 全部のミニバッチで学習する = 1epoch ? 一度に扱うデータが小さくなるので学習しやすい ? ランダム性を持つので局所最適解に陥りにくくなる
- 31. 31 DRBM
- 32. 32 ( 中間層が連続値 ) のとき汎化能力は最も高い 多値化制限ボルツマンマシン DRBM において中間層の多値拡張を行うと 汎化能力が向上する 中間層 2 : [Y . Yokoyama, T. Katsumata, & M. Yasuda, The Review of Socionetwork Strategies, 2019] DRBM(S) の hj 従来の hj DRBM(∞) を元にさらなる汎化能力の向上を目指す 先行研究 [2] -1 +1 +1 -1 0 -0.66 +0.66 -1 +1 … [-1, +1] S = 2 S = 3 S = 4 S = ∞
- 33. 33 汎化能力を向上させる方針 DRBM において中間層の多値拡張を行うと汎化能力が向上する ( 中間層が連続値 ) のとき汎化能力は最も高い 先行研究 [1] 1: [Y . Yokoyama, T. Katsumata, & M. Yasuda, The Review of Socionetwork Strategies, 2019] -1 +1 +1 -1 0 -0.66 +0.66 -1 +1 … [-1, +1] S = 2 S = 3 S = 4 S = ∞ … 出力変数のカテゴリ数 K … 問題に対して適切な数 m … 入力変数の次元数 n DBM の素子数 m が大きいと複雑な問題に対応できるようになる 一方でデータの些細な違いを重視してしまい 急激に汎化能力が低下する m の調整を簡単にできないだろうか ?
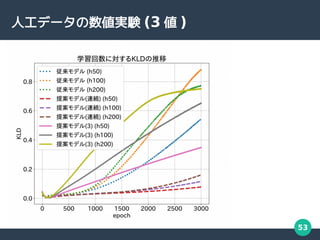
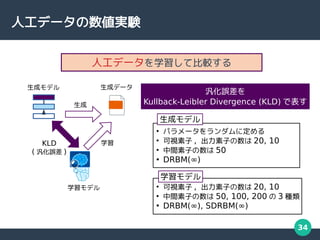
- 34. 34 人工データの数値実験 人工データを学習して比較する 汎化誤差を Kullback-Leibler Divergence (KLD) で表す 生成 KLD ( 汎化誤差 ) 学習 生成データ 生成モデル 学習モデル ● パラメータをランダムに定める ● 可視素子 , 出力素子の数は 20, 10 ● 中間素子の数は 50 ● DRBM(∞) ● 可視素子 , 出力素子の数は 20, 10 ● 中間素子の数は 50, 100, 200 の 3 種類 ● DRBM(∞), SDRBM(∞) 生成モデル 学習モデル
- 35. 35 スパースパラメータの動作の確認 中間素子の数が増えるにつれ 抑制度も全体的に増加している スパース正則化項は 中間素子を 抑制できている 右に移動 [ 勝亦 , 安田 , 情報処理学会第 82 回全国大会 , 2020] スパース正則化項が中間素子を 抑制する度合いを確認する スパース項が パラメータの影響を抑制する 度合いを表す 抑制度
- 36. 36 手書き数字画像での数値実験 ( 素子数変更 ) 汎化能力は 向上していると言える 実験条件 ? γj=10 から学習開始 ? 100 回の試行の平均をプロット ? パラメータ b,c,w,v,γ の ? 更新法は Adamax 訓練誤差 … 増加 テスト誤差 … 減少 減 増 [ 勝亦 , 安田 , 情報処理学会第 82 回全国大会 , 2020] 比較対象に Energy function constraint SDRBM(ESDRBM)[1] を使った ( 提案法よりも単純なスパース法 ) 1 : [J.Wei, J.Lv & Z.Yi, International Journal of Pattern Recognition and Artificial Intelligence, 2019]
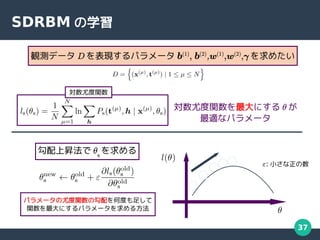
- 37. 37 SDRBM の学習 観測データ D を表現するパラメータ b(1) , b(2) ,w(1) ,w(2) ,γ を求めたい 対数尤度関数 対数尤度関数を最大にする θ が 最適なパラメータ 勾配上昇法で θs を求める ε: 小さな正の数 パラメータの尤度関数の勾配を何度も足して 関数を最大にするパラメータを求める方法
- 38. 38 人工データの数値実験 人工データを学習して比較する 生成モデル : 学習モデル : 入力 x に対する KLD 汎化誤差を Kullback-Leibler Divergence; KLD で表す 生成 KLD ( 汎化誤差 ) 学習 生成データ 生成モデル 学習モデル パラメータをランダムに決めた DRBM(∞) を生成モデルとする D(x) の 平均を近似計算する
- 40. 40 DBM
- 41. 41 DBM の学習 DBM の学習は対数尤度の最大化で行う 従来法 [1] … モンテカルロ積分 … 平均場近似 … 空間モンテカルロ積分 提案法 [2] 1 : [R. Salakhutdinov & G. Hinton, Artificial intelligence and statistics, 2009] 2 : [T. Katsumata & M. Yasuda, Nonlinear Theory and Its Applications (NOLTA 2020), 2020] DBM の期待値近似 : データ点 : 厳密和 厳密和は指数時間の計算量 近似計算が必要 DBM の勾配式
- 42. 42 DBM の応用例 – Multimodal Learning with DBM[1] – Shape Boltzmann Machine[2] 1 : [N. Srivastava & R. Salakhutdinov, Proceedings of the 25th International Conference on Neural Information Processing Systems, 2014] 2 : [S. M. Ali Eslami, Nicolas Heess, Christopher K. I. Williams, & John Winn, International Journal of Computer Vision, 2013]
- 43. 43 空間モンテカルロ積分法 : 厳密和 : データ点 厳密性 高 低 計算量 大 小 厳密計算 空間モンテカルロ積分法 [1,2] (1-SMCI) モンテカルロ積分法 空間モンテカルロ法では厳密和の範囲を調整できる 範囲が広くなるほど近似精度が高くなることが証明されている 1 : [M. Yasuda, Journal of the Physical Society of Japan, 2015] 2 : [M. Yasuda & K. Uchizawa, arXiv:2009.02165, 2020]
- 44. 44 DBM の期待値計算 DBM の期待値計算は計算困難 v と h が取りうる全ての値の総和 指数時間の計算が必要 DBM の Fine-Tuning では近似が必要 従来法 [1] … モンテカルロ積分 … 平均場近似 … 空間モンテカルロ積分 提案法 [2] 1 : [R. Salakhutdinov & G. Hinton, Artificial intelligence and statistics, 09] 2 : [T. Katsumata & M. Yasuda, Nonlinear Theory and Its Applications (NOLTA 2020), 20]
- 45. 45 空間モンテカルロ法 (MCI) … サンプリング点の 標本平均で 期待値を近似 期待値 をサンプリング点から近似したい モンテカルロ積分 (MonteCarlo-Integration; MCI) -1 1 -1 -1 1 1 r 層 r+1 層 S : サンプリング数 サンプリング
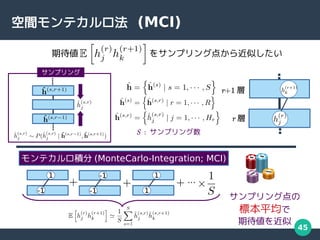
- 46. 46 空間モンテカルロ法 -1 -1 1 … 隣接するサンプリング点を条件とした 確率分布の期待値を厳密に計算 単なる標本平均よりも高精度な期待値近似が可能 [M. Yasuda, Monte Carlo Integration Using Spatial Structure of Markov Random Field, 2015] [M. Yasuda, Learning Algorithm of Boltzmann Machine Based on Spatial Monte Carlo Integration Method, 2018] 空間モンテカルロ法 (Spartial-MCI; SMCI) 1 1 -1 1 1 -1 1 -1 1 1 -1 -1 -1 1 -1 -1 1 1 -1 -1 -1 -1 1 -1 1 -1 1 1 -1 1 -1 1 -1 : サンプル点 : 厳密計算 図は 1 次の空間モンテカルロ法 (1-SMCI)
- 47. 47 Spatial Monte Carlo Integration(SMCI) 総和領域 サンプル領域 1 : [M. Yasuda, Journal of the Physical Society of Japan, 15] 2 : [M. Yasuda & K. Uchizawa, arXiv:2009.02165, 20] SMCI[1,2] は厳密和とサンプル近似を組み合わせた近似方法 : サンプル近似 : 厳密和 目標領域 総和領域内の期待値を厳密和 サンプル領域内の期待値をサンプル近似 目標領域と総和領域が同じとき 1-SMCI と呼ぶ 総和領域に隣接ノードが増えるたびに 2,3,..-SMCI となる 総和領域が広いほど近似精度は向上する
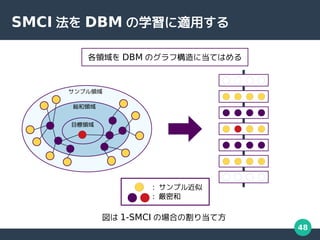
- 48. 48 SMCI 法を DBM の学習に適用する 総和領域 サンプル領域 目標領域 各領域を DBM のグラフ構造に当てはめる : サンプル近似 : 厳密和 図は 1-SMCI の場合の割り当て方
- 49. 49 パターン認識問題への応用 データをあらかじめ決められたカテゴリに分類する問題 パターン認識問題 8 です ● v を 2 つに分割する ● x が実数値を 取れるようにする 28%! RBM の機能 -1 1 -1 1 生成 確率
- 50. 50 DBM の学習 第 1 項 , 第 2 項ともに厳密計算は不可能 DBM も勾配上昇法で学習したい . しかし… 対数尤度関数の勾配 近似学習アルゴリズムで学習する -1 -1 -1 -1 -1 -1 -1 1 1 1 1 1 … 通り
- 51. 51 近似学習アルゴリズム … 平均場近似 … モンテカルロ積分 従来の方法 ? 厳密な値を計算することなく 学習できる ? 近似が荒く学習精度が悪い ? 多値化を行ったとき 別々の方法で定式化する必要がある … 空間モンテカルロ法 提案法 両方とも ? 両方の項で同じ式を 使うことができる ? 近似性能が高いことが知られている (DBM では未確認 ) 多値化の前に , より良い近似学習アルゴリズムを確立させる [M. Yasuda, Monte Carlo Integration Using Spatial Structure of Markov Random Field, 2015] [M. Yasuda, Learning Algorithm of Boltzmann Machine Based on Spatial Monte Carlo Integration Method, 2018]
- 52. 52 数値実験 人工データを使った数値実験を行う Kullback-Leibler Divergence (KLD) 汎化誤差 (→ 低いほど良い ) 対数尤度 モデルがデータを表す度合い (→ 高いほど良い ) 生成 KLD 対数尤度 人工データ gDBM tDBM 確認する指標 パラメータは から生成 (Oin, Oout は隣接する層の素子数 ) パラメータは Xavier の方法 [1] で生成 生成モデル 学習モデル 従来法 , 1-SMCI, semi 2-SMCI, 厳密値による学習の 4 つの方法を比較する 1 : [X. Glorot & Y . Bengio, Proceedings of the 13th International Conference on Artificial Intelligence and Statistics, 2010.] 生成?学習モデルともに小さめのモデルを使用する ( 指標の計算のため )
- 53. 53 人工データの数値実験 (3 値 )

![3
研究の概観
2 つのモデルに対して
異なるアプローチから汎化能力の向上を目指す
1. 制限ボルツマンマシン分類器 [1,2]
モデルの拡張
中間層のスパース正則化 [3]
2. 深層ボルツマンマシン [4]
空間モンテカルロ法 [5,6]
を使った学習法 [7]
学習アルゴリズムの改善
1 : [H. Larochelle & Y. Bengio, 2008]
2 : [H. Larochelle et al., 2012]
3 : [ 勝亦利宗 , 安田宗樹 , 2020]
4 : [R. Salakhutdinov & G. Hinton, 2009]
5 : [M. Yasuda, 2015]
6 : [M. Yasuda & K. Uchizawa, 2020]
7 : [T. Katsumara & M. Yasuda, 2020]](https://image.slidesharecdn.com/middle-211007103314/85/-3-320.jpg)

![5
制限ボルツマンマシン分類器
Discriminative Restricted Boltzmann Machine (DRBM)[1,2,3]
出力層
中間層
入力層
DRBM の確率分布関数
1 : [H. Larochelle & Y
. Bengio, Proceedings of the 25th international conference on Machine learning, 2008]
2 : [H. Larochelle, M. Mandel, R. Pascanu, & Y
. Bengio, The Journal of Machine Learning Research, 2012]
3: [Y
. Yokoyama, T. Katsumata, & M. Yasuda, The Review of Socionetwork Strategies, 2019]
m が大きい
過学習は強くなる
中間素子の数 m が
モデルの表現能力を決める](https://image.slidesharecdn.com/middle-211007103314/85/-5-320.jpg)
![7
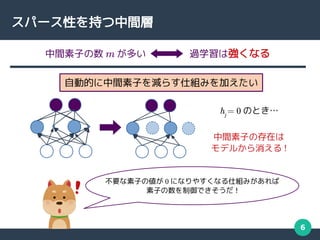
スパース性を持つ中間層 ( 提案モデル )
スパース正則化項
スパース正則化 DRBM(Sparse-DRBM; SDRBM)
γj
の最適な値は尤度関数の最大化によって求めることができる
スパース項の働きで
h は 0 を取りやすくなる
h
確率密度
突出
モデルは自動的に不要な素子を削減できる !
[ 勝亦 , 安田 , 情報処理学会第82回全国大会 , 2020]
従来法
提案法
γj
が大きい
hj
=0 の確率が高くなる
→](https://image.slidesharecdn.com/middle-211007103314/85/-7-320.jpg)
![8
人工データでの数値実験
提案モデルの
汎化能力は向上している
全体的に汎化誤差は低下
[ 勝亦 , 安田 , 情報処理学会第 82 回全国大会 , 2020]
汎化誤差
(KLD)
汎化誤差を
Kullback-Leibler Divergence (KLD)
で表す
生成
KLD
( 汎化誤差 )
学習
事前に決めた
パラメータ](https://image.slidesharecdn.com/middle-211007103314/85/-8-320.jpg)
![10
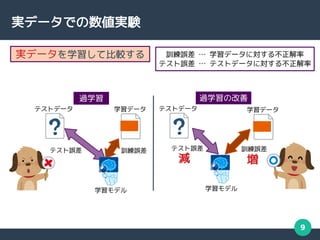
数値実験 (MNIST)
訓練誤差 … 増加
テスト誤差 … 減少
down
up
[ 勝亦 , 安田 , 情報処理学会第 82 回全国大会 , 2020]
比較対象に Energy function constraint SDRBM(ESDRBM)[1]
を使った ( 提案法よりも単純なスパース法 )
1:[J.Wei, J.Lv & Z.Yi, International Journal of Pattern Recognition and Artificial Intelligence, 2019]
MNIST と呼ばれる
手書き数字画像
データセット
学習データ
汎化能力は
向上していると言える
Fashion-MNIST や
CIFAR-10 などの
データセットでも
同様の結果が得られた](https://image.slidesharecdn.com/middle-211007103314/85/-10-320.jpg)

![13
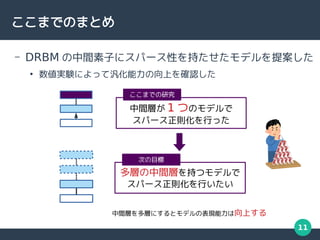
Deep Boltzmann Machine[1]
(DBM)
隠れ層 : 確率変数の層
可視層 : データを入力する層
L は隠れ層の数 , Hr
は r 番目の隠れ層の素子数
1 : [R. Salakhutdinov & G. Hinton, Artificial intelligence and statistics, 2009]
DBM の確率関数](https://image.slidesharecdn.com/middle-211007103314/85/-13-320.jpg)
![15
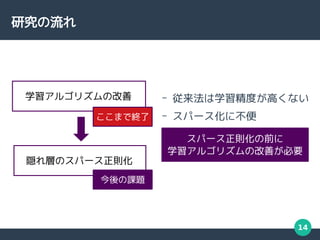
DBM の学習
DBM の学習は勾配法による対数尤度の最大化で行う
1 : [R. Salakhutdinov & G. Hinton, Artificial intelligence and statistics, 2009]
2 : [T. Katsumata & M. Yasuda, Nonlinear Theory and Its Applications (NOLTA 2020), 2020]
DBM の勾配式
可視層を
データで固定した
モデルの期待値
可視層を
データで固定しない
モデルの期待値
: データ点
: 厳密和
= -
平均場近似法 モンテカルロ積分法
従来法 [1]
空間モンテカルロ積分法
提案法 [2]
勾配法は勾配の値を逐次的に加算する方法
厳密和の計算には指数時間の計算量が必要
( 勾配 )](https://image.slidesharecdn.com/middle-211007103314/85/-15-320.jpg)
![16
提案アルゴリズムによる学習結果
1:[T. Katsumata & M.Yasuda, Proceedings of
the 2020 International Symposium on
Nonlinear Theory and Its Applications (NOLTA
2020), pp.29-32, 2020]
2:[T. Katsumata & M.Yasuda, Nonlinear
Theory and Its Applications (NOLTA 2020),
IEICE, 2020] 【投稿中】
down
up
up
down
3 層の結果 [1]
両方の指標ともに従来法よりも
良い結果が得られている
生成
KLD
( 良い→低い )
対数尤度
( 良い→高い )
事前に決めた
パラメータ
4 層の結果 [2]](https://image.slidesharecdn.com/middle-211007103314/85/-16-320.jpg)



![22
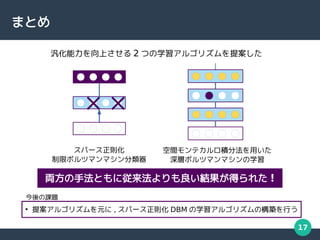
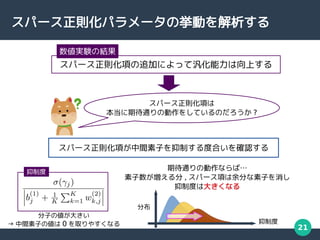
実験結果
中間素子の数が増えるにつれ
抑制度も全体的に増加している
スパース正則化項は
余分な中間素子を
抑制している
右に移動
[ 勝亦 , 安田 , 情報処理学会第 82 回全国大会 , 2020]](https://image.slidesharecdn.com/middle-211007103314/85/-22-320.jpg)

![24
数値実験 (Fashion-MNIST)
訓練誤差 … 増加
テスト誤差 … 減少
down
up
比較対象に Energy function constraint SDRBM(ESDRBM)[1]
を使った ( 提案法よりも単純なスパース法 )
1:[J.Wei, J.Lv & Z.Yi, International Journal of Pattern Recognition and Artificial Intelligence, 2019]
Fashion-MNIST
服や靴などの
画像の分類
学習データ
素子数は 100](https://image.slidesharecdn.com/middle-211007103314/85/-24-320.jpg)

![26
数値実験 (CIFAR-10)
汎化能力は
向上していると言える
訓練誤差 … 増加
テスト誤差 … 減少
down
up
比較対象に Energy function constraint SDRBM(ESDRBM)[1]
を使った ( 提案法よりも単純なスパース法 )
1:[J.Wei, J.Lv & Z.Yi, International Journal of Pattern Recognition and Artificial Intelligence, 2019]
CIFAR-10
動物や乗り物などの
画像の分類
学習データ
素子数は 200](https://image.slidesharecdn.com/middle-211007103314/85/-26-320.jpg)



![32
( 中間層が連続値 ) のとき汎化能力は最も高い
多値化制限ボルツマンマシン
DRBM において中間層の多値拡張を行うと
汎化能力が向上する
中間層
2 : [Y
. Yokoyama, T. Katsumata, & M. Yasuda, The Review of Socionetwork Strategies, 2019]
DRBM(S) の hj
従来の hj
DRBM(∞) を元にさらなる汎化能力の向上を目指す
先行研究 [2]
-1 +1
+1
-1 0
-0.66 +0.66
-1 +1
…
[-1, +1]
S = 2
S = 3
S = 4
S = ∞](https://image.slidesharecdn.com/middle-211007103314/85/-32-320.jpg)
![33
汎化能力を向上させる方針
DRBM において中間層の多値拡張を行うと汎化能力が向上する
( 中間層が連続値 ) のとき汎化能力は最も高い
先行研究 [1]
1: [Y
. Yokoyama, T. Katsumata, & M. Yasuda, The Review of Socionetwork Strategies, 2019]
-1 +1
+1
-1 0
-0.66 +0.66
-1 +1
…
[-1, +1]
S = 2
S = 3
S = 4
S = ∞
… 出力変数のカテゴリ数 K
… 問題に対して適切な数 m
… 入力変数の次元数 n
DBM の素子数
m が大きいと複雑な問題に対応できるようになる
一方でデータの些細な違いを重視してしまい
急激に汎化能力が低下する
m の調整を簡単にできないだろうか ?](https://image.slidesharecdn.com/middle-211007103314/85/-33-320.jpg)
![35
スパースパラメータの動作の確認
中間素子の数が増えるにつれ
抑制度も全体的に増加している
スパース正則化項は
中間素子を
抑制できている
右に移動
[ 勝亦 , 安田 , 情報処理学会第 82 回全国大会 , 2020]
スパース正則化項が中間素子を
抑制する度合いを確認する
スパース項が
パラメータの影響を抑制する
度合いを表す
抑制度](https://image.slidesharecdn.com/middle-211007103314/85/-35-320.jpg)
![36
手書き数字画像での数値実験 ( 素子数変更 )
汎化能力は
向上していると言える
実験条件
? γj=10 から学習開始
?
100 回の試行の平均をプロット
?
パラメータ b,c,w,v,γ の
?
更新法は Adamax
訓練誤差 … 増加
テスト誤差 … 減少
減
増
[ 勝亦 , 安田 , 情報処理学会第 82 回全国大会 , 2020]
比較対象に Energy function
constraint SDRBM(ESDRBM)[1]
を使った ( 提案法よりも単純なスパース法 )
1 : [J.Wei, J.Lv & Z.Yi, International Journal of Pattern Recognition and Artificial Intelligence, 2019]](https://image.slidesharecdn.com/middle-211007103314/85/-36-320.jpg)


![41
DBM の学習
DBM の学習は対数尤度の最大化で行う
従来法 [1]
… モンテカルロ積分
… 平均場近似
… 空間モンテカルロ積分
提案法 [2]
1 : [R. Salakhutdinov & G. Hinton, Artificial intelligence and statistics, 2009]
2 : [T. Katsumata & M. Yasuda, Nonlinear Theory and Its Applications (NOLTA 2020), 2020]
DBM の期待値近似
: データ点
: 厳密和
厳密和は指数時間の計算量
近似計算が必要
DBM の勾配式](https://image.slidesharecdn.com/middle-211007103314/85/-41-320.jpg)
![42
DBM の応用例
– Multimodal Learning with DBM[1]
– Shape Boltzmann Machine[2]
1 : [N. Srivastava & R. Salakhutdinov, Proceedings of the 25th International Conference on Neural
Information Processing Systems, 2014]
2 : [S. M. Ali Eslami, Nicolas Heess, Christopher K. I. Williams, & John Winn, International Journal of
Computer Vision, 2013]](https://image.slidesharecdn.com/middle-211007103314/85/-42-320.jpg)
![43
空間モンテカルロ積分法
: 厳密和
: データ点
厳密性
高 低
計算量
大 小
厳密計算 空間モンテカルロ積分法 [1,2]
(1-SMCI)
モンテカルロ積分法
空間モンテカルロ法では厳密和の範囲を調整できる
範囲が広くなるほど近似精度が高くなることが証明されている
1 : [M. Yasuda, Journal of the Physical Society of Japan, 2015]
2 : [M. Yasuda & K. Uchizawa, arXiv:2009.02165, 2020]](https://image.slidesharecdn.com/middle-211007103314/85/-43-320.jpg)
![44
DBM の期待値計算
DBM の期待値計算は計算困難
v と h が取りうる全ての値の総和
指数時間の計算が必要
DBM の Fine-Tuning では近似が必要
従来法 [1]
… モンテカルロ積分
… 平均場近似
… 空間モンテカルロ積分
提案法 [2]
1 : [R. Salakhutdinov & G. Hinton, Artificial intelligence and statistics, 09]
2 : [T. Katsumata & M. Yasuda, Nonlinear Theory and Its Applications (NOLTA 2020), 20]](https://image.slidesharecdn.com/middle-211007103314/85/-44-320.jpg)
![46
空間モンテカルロ法
-1 -1 1
…
隣接するサンプリング点を条件とした
確率分布の期待値を厳密に計算
単なる標本平均よりも高精度な期待値近似が可能
[M. Yasuda, Monte Carlo Integration Using Spatial Structure of Markov Random Field, 2015]
[M. Yasuda, Learning Algorithm of Boltzmann Machine Based on Spatial Monte Carlo Integration Method, 2018]
空間モンテカルロ法 (Spartial-MCI; SMCI)
1 1 -1
1 1 -1
1 -1 1
1 -1 -1
-1 1 -1
-1 1 1
-1 -1 -1
-1 1 -1
1 -1 1
1 -1 1
-1 1 -1
: サンプル点
: 厳密計算
図は 1 次の空間モンテカルロ法 (1-SMCI)](https://image.slidesharecdn.com/middle-211007103314/85/-46-320.jpg)
![47
Spatial Monte Carlo Integration(SMCI)
総和領域
サンプル領域
1 : [M. Yasuda, Journal of the Physical Society of Japan, 15]
2 : [M. Yasuda & K. Uchizawa, arXiv:2009.02165, 20]
SMCI[1,2]
は厳密和とサンプル近似を組み合わせた近似方法
: サンプル近似
: 厳密和
目標領域
総和領域内の期待値を厳密和
サンプル領域内の期待値をサンプル近似
目標領域と総和領域が同じとき 1-SMCI と呼ぶ
総和領域に隣接ノードが増えるたびに 2,3,..-SMCI となる
総和領域が広いほど近似精度は向上する](https://image.slidesharecdn.com/middle-211007103314/85/-47-320.jpg)
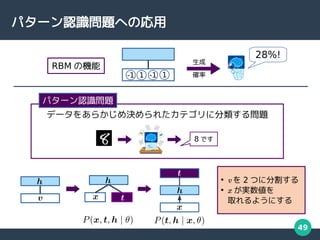

![51
近似学習アルゴリズム
… 平均場近似
… モンテカルロ積分
従来の方法 ? 厳密な値を計算することなく
学習できる
? 近似が荒く学習精度が悪い
? 多値化を行ったとき
別々の方法で定式化する必要がある
… 空間モンテカルロ法
提案法
両方とも
? 両方の項で同じ式を
使うことができる
? 近似性能が高いことが知られている
(DBM では未確認 )
多値化の前に , より良い近似学習アルゴリズムを確立させる
[M. Yasuda, Monte Carlo Integration Using Spatial Structure of Markov Random Field, 2015]
[M. Yasuda, Learning Algorithm of Boltzmann Machine Based on Spatial Monte Carlo Integration Method, 2018]](https://image.slidesharecdn.com/middle-211007103314/85/-51-320.jpg)
![52
数値実験
人工データを使った数値実験を行う
Kullback-Leibler Divergence (KLD)
汎化誤差 (→ 低いほど良い )
対数尤度
モデルがデータを表す度合い (→ 高いほど良い )
生成
KLD 対数尤度
人工データ
gDBM
tDBM
確認する指標
パラメータは
から生成
(Oin,
Oout
は隣接する層の素子数 )
パラメータは
Xavier の方法 [1]
で生成
生成モデル 学習モデル
従来法 , 1-SMCI, semi 2-SMCI, 厳密値による学習の 4 つの方法を比較する
1 : [X. Glorot & Y
. Bengio, Proceedings of the 13th International Conference on Artificial Intelligence and Statistics, 2010.]
生成?学習モデルともに小さめのモデルを使用する ( 指標の計算のため )](https://image.slidesharecdn.com/middle-211007103314/85/-52-320.jpg)