–Ы–Є–љ–µ–∞—А–љ–Є —А–∞–≤–µ–љ–Ї–Є
- 3. пВЮ –†–∞–≤–µ–љ—Б—В–≤–∞—В–∞ –≤–Њ –Ї–Њ–Є –ї–µ–≤–∞—В–∞ –Є –і–µ—Б–љ–∞—В–∞ —Б—В—А–∞–љ–∞ —Б–µ –±—А–Њ—Ш–љ–Є –Є–Ј—А–∞–Ј–Є —Б–µ –≤–Є–Ї–∞–∞—В –±—А–Њ—Ш–љ–Є —А–∞–≤–µ–љ—Б—В–≤–∞. пВЮ –†–∞–≤–µ–љ—Б—В–≤–∞—В–∞ –≤–Њ –Ї–Є–Њ –ї–µ–≤–∞—В–∞ –Є –і–µ—Б–љ–∞—В–∞ —Б—В—А–∞–љ–∞ –Є–ї–Є –±–∞—А–µ–Љ –µ–і–љ–∞ –Њ–і –љ–Є–≤ –µ –Є–Ј—А–∞–Ј —Б–Њ –њ—А–Њ–Љ–µ–љ–ї–Є–≤–∞, —Б–µ –≤–Є–Ї–∞–∞—В —А–∞–≤–µ–љ—Б—В–≤–∞ —Б–Њ –њ—А–Њ–Љ–µ–љ–ї–Є–≤–Є. –Я—А–Њ–Љ–µ–љ–ї–Є–≤–Є—В–µ —Б–µ –Љ–µ–љ—Г–≤–∞–∞—В –≤–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ R –Є–ї–Є –≤–Њ –љ–µ–Ї–Њ–µ –љ–µ–≥–Њ–≤–Њ –њ–Њ–і–Љ–љ–Њ–ґ–µ—Б—В–≤–Њ. пВЮ –Ь–љ–Њ–ґ–µ—Б—В–≤–Њ –≤–Њ –Ї–Њ–µ —Б–µ –Љ–µ–љ—Г–≤–∞–∞—В –њ—А–Њ–Љ–µ–љ–ї–Є–≤–Є—В–µ —Б–µ –≤–Є–Ї–∞ –і–µ—Д–Є–љ–Є—Ж–Є–Њ–љ–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –Є –љ–∞—Ш—З–µ—Б—В–Њ —Б–µ –Њ–Ј–љ–∞—З—Г–≤–∞ —Б–Њ D.
- 4. –†–∞–≤–µ–љ—Б—В–≤–Њ —Б–Њ –µ–і–љ–∞ –њ—А–Њ–Љ–µ–љ–ї–Є–≤–∞, –≤–Њ –Њ–њ—И—В —Б–ї—Г—З–∞—Ш —Ь–µ –Њ–Ј–љ–∞—З—Г–≤–∞–Љ–µ —Б–Њ –Р(—Е) = –Т(—Е), ѕµ D, –Ї–∞–і–µ —И—В–Њ –Р(—Е) –Є –Т(—Е) —Б–µ –Є–Ј—А–∞–Ј–Є —Б–Њ –њ—А–Њ–Љ–µ–љ–ї–Є–≤–∞ —Е, –і—Д–Є–љ–Є—А–∞–љ–Є –≤–Њ D. –Я–Њ–љ–∞—В–∞–Љ—Г, –∞–Ї–Њ –љ–µ –µ –Ј–∞–і–∞–і–µ–љ–Њ –і–µ—Д–Є–љ–Є—Ж–Є–Њ–љ–Њ—В–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ —Ь–µ –њ–Њ–і—А–∞–Ј–±–µ—А–µ–Љ–µ –і–µ–Ї–∞ —В–Њ–∞ –µ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ R –љ–∞ —А–µ–∞–ї–љ–Є—В–µ –±—А–Њ–µ–≤–Є.
- 6. –°–њ–Њ—А–µ–і –±—А–Њ—Ш–Њ—В –љ–∞ –љ–µ–њ–Њ–Ј–љ–∞—В–Є—В–µ, —А–∞–≤–µ–љ–Ї–Є—В–µ –Љ–Њ–ґ–∞—В –і–∞ –±–Є–і–∞—В: —А–∞–≤–µ–љ–Ї–Є —Б–Њ –µ–і–љ–∞ –љ–µ–њ–Њ–Ј–љ–∞—В–∞, —А–∞–≤–µ–љ–Ї–Є —Б–Њ –і–≤–µ –љ–µ–њ–Њ–Ј–љ–∞—В–Є, —А–∞–≤–µ–љ–Ї–Є —Б–Њ —В—А–Є –љ–µ–њ–Њ–Ј–љ–∞—В–Є –Є—В–љ. –°–њ–Њ—А–µ–і —З–ї–µ–љ–Њ—В —Б–Њ –љ–∞—Ш–≤–Є—Б–Њ–Ї —Б—В–µ–њ–µ–љ, —А–∞–≤–µ–љ–Ї–Є—В–µ –Љ–Њ–ґ–∞—В –і–∞ –±–Є–і–∞—В: —А–∞–≤–µ–љ–Ї–Є –Њ–і –њ—А–≤ —Б—В–µ–њ–µ–љ–ї–Є–љ–µ–∞—А–љ–Є, —А–∞–≤–µ–љ–Ї–Є –Њ–і –≤—В–Њ—А —Б—В–µ–њ–µ–љ-–Ї–≤–∞–і—А–∞—В–љ–Є, —А–∞–≤–µ–љ–Ї–Є –Њ–і —В—А–µ—В —Б—В–µ–њ–µ–љ-–Ї—Г–±–љ–Є .
- 8. –°–µ–Ї–Њ—Ш–∞ –≤—А–µ–і–љ–Њ—Б—В –љ–∞ –љ–µ–њ–Њ–Ј–љ–∞—В–∞—В–∞ –Ј–∞ –Ї–Њ—Ш–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ –њ—А–µ–Љ–Є–љ—Г–≤–∞ –≤–Њ —В–Њ—З–љ–Њ –±—А–Њ—Ш–љ–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ —Б–µ –≤–Є–Ї–∞ —А–µ—И–µ–љ–Є–µ –Є–ї–Є –Ї–Њ—А–µ–љ –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞.
- 9. вАҐ–Ф–∞ —Б–µ —А–µ—И–Є –µ–і–љ–∞ —А–∞–≤–µ–љ–Ї–∞ –Ј–љ–∞—З–Є –і–∞ —Б–µ –љ–∞—Ш–і–∞—В —Б–Є—В–µ –љ–µ—Ш–Ј–Є–љ–Є —А–µ—И–µ–љ–Є—Ш–∞. вАҐ–°–Є—В–µ —А–µ—И–µ–љ–Є—Ш–∞ –љ–∞ –µ–і–љ–∞ —А–∞–≤–µ–љ–Ї–∞ –Њ–±—А–∞–Ј—Г–≤–∞–∞—В –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –Ї–Њ–µ —Б–µ –≤–Є–Ї–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ —А–µ—И–µ–љ–Є—Ш–∞ –љ–∞ —В–∞–∞ —А–∞–≤–µ–љ–Ї–∞. вАҐ–Ь–љ–Њ–ґ–µ—Б—В–≤–Њ—В–Њ —А–µ—И–µ–љ–Є—Ш–∞ –љ–∞ –µ–і–љ–∞ —А–∞–≤–µ–љ–Ї–∞ –љ–∞—Ш—З–µ—Б—В–Њ —Б–µ –Њ–Ј–љ–∞—З—Г–≤–∞–∞—В —Б–Њ –Ь. –Э–∞ –њ—А–Є–Љ–µ—А, –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ—В–Њ —А–µ—И–µ–љ–Є—Ш–∞ –љ–∞ –µ–і–љ–∞ —А–∞–≤–µ–љ–Ї–∞ 12 - 2—Е = —Е вАУ 3, —Е ѕµ {3, 5, 7} –µ –Ь = {5}, –∞ –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ —Е¬≤ + 6 = 5—Е, —Е ѕµ {0, 1, 2, 3} –µ –Ь = {2, 3}.
- 10. –Ф–≤–µ —А–∞–≤–µ–љ–Ї–Є —Б–Њ –Є—Б—В–Њ –і–µ—Д–Є–љ–Є—Ж–Є–Њ–љ–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ —И—В–Њ –Є–Љ–∞–∞—В –µ–і–љ–∞–Ї–≤–Є –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ —А–µ—И–µ–љ–Є—Ш–∞ —Б–µ –≤–Є–Ї–∞–∞—В –µ–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Є —А–∞–≤–µ–љ–Ї–Є.
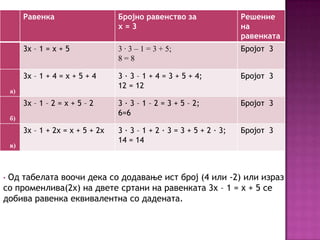
- 12. –†–∞–≤–µ–љ–Ї–∞ –С—А–Њ—Ш–љ–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ –Ј–∞ —Е=3 –†–µ—И–µ–љ–Є–µ –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ 3—Е вАУ 1 = —Е + 5 3 вИЩ 3 вАУ 1 = 3 + 5; 8=8 –С—А–Њ—Ш–Њ—В 3 3—Е вАУ 1 + 4 = —Е + 5 + 4 3 вИЩ 3 вАУ 1 + 4 = 3 + 5 + 4; 12 = 12 –С—А–Њ—Ш–Њ—В 3 3—Е вАУ 1 вАУ 2 = —Е + 5 вАУ 2 3 вИЩ 3 вАУ 1 вАУ 2 = 3 + 5 вАУ 2; 6=6 –С—А–Њ—Ш–Њ—В 3 3—Е вАУ 1 + 2—Е = —Е + 5 + 2—Е 3 вИЩ 3 вАУ 1 + 2 вИЩ 3 = 3 + 5 + 2 вИЩ 3; 14 = 14 –С—А–Њ—Ш–Њ—В 3 –∞) –±) –≤) –Ю–і —В–∞–±–µ–ї–∞—В–∞ –≤–Њ–Њ—З–Є –і–µ–Ї–∞ —Б–Њ –і–Њ–і–∞–≤–∞—Ъ–µ –Є—Б—В –±—А–Њ—Ш (4 –Є–ї–Є -2) –Є–ї–Є –Є–Ј—А–∞–Ј —Б–Њ –њ—А–Њ–Љ–µ–љ–ї–Є–≤–∞(2—Е) –љ–∞ –і–≤–µ—В–µ —Б—А—В–∞–љ–Є –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ 3—Е вАУ 1 = —Е + 5 —Б–µ –і–Њ–±–Є–≤–∞ —А–∞–≤–µ–љ–Ї–∞ –µ–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–∞ —Б–Њ –і–∞–і–µ–љ–∞—В–∞. вАҐ
- 13. –Р–Ї–Њ –Ї–Њ–љ –ї–µ–≤–∞—В–∞ –Є –і–µ—Б–љ–∞—В–∞ —Б—В—А–∞–љ–∞ –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ –Р(—Е) = –Т(—Е) —Б–µ –і–Њ–і–∞–і–µ –Є—Б—В –±—А–Њ—Ш —Б —Ф R –Є–ї–Є –Є–Ј—А–∞–Ј –°(—Е) —Б–Њ –њ—А–Њ–Љ–µ–љ–ї–Є–≤–∞ —Е, –Ї–Њ—Ш—И—В–Њ –µ –Њ–њ—А–µ–і–µ–ї–µ–љ –Ј–∞ —Б–µ–Ї–Њ—Ш —Е –Њ–і –і–µ—Д–Є–љ–Є—Ж–Є–Њ–љ–Њ—В–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞, —Б–µ –і–Њ–±–Є–≤–∞ —А–∞–≤–µ–љ–Ї–∞ –µ–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–∞ —Б–Њ –і–∞–і–µ–љ–∞—В–∞. –Ч–∞–њ–Є—И—Г–≤–∞–Љ–µ: –Р(—Е) = –Т(—Е) –Р(—Е) + –°(—Е) = –Т(—Е) + –°(—Е)
- 14. –Я¬є –°–µ–Ї–Њ—Ш —З–ї–µ–љ –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ—А–µ–љ–µ—Б–µ –Њ–і –µ–і–љ–∞ —Б—В—А–∞–љ–∞ –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ –љ–∞ –і—А—Г–≥–∞, –љ–Њ —Б–Њ —Б–њ—А–Њ—В–Є–≤–µ–љ –Ј–љ–∞–Ї. –Я¬≤ –Р–Ї–Њ –љ–∞ –і–≤–µ—В–µ —Б—В—А–∞–љ–Є –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ –Є–Љ–∞ –µ–і–љ–∞–Ї–≤–Є —З–ї–µ–љ–Њ–≤–Є, —В–Њ–≥–∞—И —В–Є–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –Є–Ј–Њ—Б—В–∞–≤–∞—В (–і–∞ —Б–µ –њ–Њ–љ–Є—И—В–∞—В).
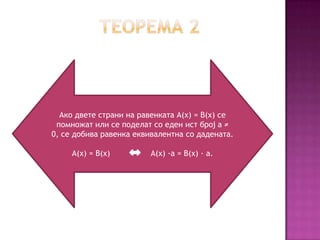
- 15. –Р–Ї–Њ –і–≤–µ—В–µ —Б—В—А–∞–љ–Є –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ –Р(—Е) = –Т(—Е) —Б–µ –њ–Њ–Љ–љ–Њ–ґ–∞—В –Є–ї–Є —Б–µ –њ–Њ–і–µ–ї–∞—В —Б–Њ –µ–і–µ–љ –Є—Б—В –±—А–Њ—Ш –∞ вЙ† 0, —Б–µ –і–Њ–±–Є–≤–∞ —А–∞–≤–µ–љ–Ї–∞ –µ–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–∞ —Б–Њ –і–∞–і–µ–љ–∞—В–∞. –Р(—Е) = –Т(—Е) –Р(—Е) вИЩ–∞ = –Т(—Е) вИЩ –∞.
- 16. –Я¬є –Р–Ї–Њ —Б–Є—В–µ —З–ї–µ–љ–Њ–≤–Є –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ —Б–µ –њ–Њ–Љ–љ–Њ–ґ–∞—В —Б–Њ 1, —В–Њ–≥–∞—И —Б–µ –і–Њ–±–Є–≤–∞ —А–∞–≤–µ–љ–Ї–∞ –µ–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–∞ –љ–∞ –і–∞–і–µ–љ–∞—В–∞, —В.–µ. –Р–Ї–Њ —Б–Є—В–µ —З–ї–µ–љ–Њ–≤–Є –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ —Б–µ –Ј–∞–Љ–µ–љ–∞—В —Б–Њ –љ–Є–≤–љ–Є—В–µ —Б–њ—А–Њ—В–Є–≤–љ–Є, —Б–µ –і–Њ–±–Є–≤–∞ —А–∞–≤–µ–љ–Ї–∞ –µ–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–∞ –љ–∞ –і–∞–і–µ–љ–∞—В–∞. –Я¬≤ –Р–Ї–Њ –љ–µ–Ї–Њ–Є —З–ї–µ–љ–Њ–≤–Є –љ–∞ —А–∞–≤–µ–љ–Ї–∞—В–∞ –Є–Љ–∞–∞—В –Є–Љ–µ–љ–Є—В–µ–ї–Є, —В–Њ–≥–∞—И –Њ–і –Є–Љ–µ–љ–Є—В–µ–ї–Є—В–µ –Љ–Њ–ґ–µ–Љ–µ –і–∞ —Б–µ –Њ—Б–ї–Њ–±–Њ–і–Є–Љ–µ –Њ–і –Љ–љ–Њ–ґ–µ—Ъ–µ –љ–∞ –і–≤–µ—В–µ —Б—В—А–∞–љ–Є –Њ–і —А–∞–≤–µ–љ–Ї–∞—В–∞ —Б–Њ –љ–Є–≤–љ–Є–Њ—В –љ–∞—Ш–Љ–∞–ї –Ј–∞–µ–і–љ–Є—З–Ї–Є —Б–Њ–і—А–ґ–∞—В–µ–ї.