狠狠撸

「パターン認識と機械学習」
輪読勉強会
～指数型分布族?ノンパラメトリック法～

自己紹介
? 名前
? 小笠原光貴(Mitsuki OGASAHARA)
? 入社年度
? 2014年度
? 所属
? (株)CyberZ 開発エンジニア
? 学生時代の研究分野
? 自然言語処理?機械学習

目次
? 2.4 指数型分布族
? 2.4.1 最尤推定と十分統計量
? 2.4.2 共役事前分布
? 2.4.3 無情報事前分布
? 2.5 ノンパラメトリック法
? 2.5.1 カーネル密度推定法
? 2.5.2 最近傍法

2.4 指数型分布族(p.110)
? 式(2.194)で定義される分布の族(集合)
!
? 「ガウス分布」「多項分布」など、?
PRMLに出てくる多くの分布が指数型分布族に含まれる?
→ 式(2.194)で定義し直すことができる
? ※ xはスカラーでもベクトルでも良い
? ※ xは離散でも連続でも良い
(2.194)

!
? : xに関する関数
? scaling constantとも呼ばれ(MLaPPより)、?
「1」が入ることもある(ベルヌーイ分布、ガンマ分布)
(2.194)
h (x)

!
? : ηに関する関数
? 確率密度関数の積分値が1になるように?
正規化するためのもの
(2.194)
g(?)
g (?)
Z
h (x) exp ?T
u (x) dx = 1 (2.195)
Z(?) =
1
g (?)
=
Z
h (x) exp ?T
u (x) dx

ベルヌーイ分布は指数型分布族か？
!
? 無理やりexpの中に入れてみる
!
!
!
? ηを式(2.198)のように定義する
Bern(x|?) = ?x
(1 ?)1 x
(2.196)
Bern(x|?) = exp{ln ?x
(1 ?)1 x
}
= exp{x ln ? + (1 x) ln 1 ?}
= exp{x(ln ? ln 1 ?) + ln 1 ?}
= (1 ?) exp{ln(
?
1 ?
)x} (2.197)
(2.198)? = ln(
?
1 ?
)

ベルヌーイ分布は指数型分布族か？
!
? 最終的には、
!
? となり、式(2.194)と対応した
Bern(x|?) = ?x
(1 ?)1 x
(2.196)
(2.197)
(2.194)

参考：指数型分布族に含まれないもの
? 混合正規分布?
?
?
?
expの和になってしまい、式(2.194)にはならない
(2.194)

2.4.1 最尤推定
? 指数型分布族の一般形の式(2.194)から、?
最尤推定量ηを求める
? 独立に同分布に従うデータ集合Xについて考えると、?
この尤度関数は
!
? 対数尤度関数は

2.4.1 最尤推定
? 対数尤度関数の(ηに関しての)勾配が0となる値を見つ
けたい
(2.228)

2.4.1 最尤推定
? 原則として、式(2.228)を解くとηは得られる
!
!
? また、最尤推定値はに依存する(十分統計量)
? 言い換えると、最尤推定を求めるためには、?
???の総和(または平均)のみがあればよい
(2.228)

最尤推定と真のパラメータ
? ηの最尤推定値は式(2.228)を解くと得られる
!
!
? の定義に基づくと、
!
!
? つまり、N→ の極限では、最尤推定値＝真の値
(2.228)
g (?)
Z
h (x) exp ?T
u (x) dx = 1 (2.195)
(2.226)

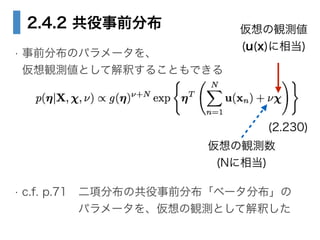
2.4.2 共役事前分布
? 指数型分布族の任意の分布について、?
次の形で書ける共役事前分布が存在する
!
? 導出は書いてないが、共役であることが確かめられる?
尤度関数(2.227)と事前分布(2.229)をかけ、?
事後分布を求める
(2.229)

? 導出は書いてないが、共役であることが確かめられる?
尤度関数(2.227)と事前分布(2.229)をかけ、?
事後分布を求める
(2.229)
(2.230)

? 事前分布のパラメータを、?
仮想観測値として解釈することもできる
!
!
!
!
? c.f. p.71?二項分布の共役事前分布「ベータ分布」の?
?????パラメータを、仮想の観測として解釈した
(2.230)
仮想の観測数?
(Nに相当)
仮想の観測値?
(u(x)に相当)

2.4.3 無情報事前分布
? 事前分布を置きたいが、分布(やパラメータ)についての?
知識がないとき
? 一様分布を置けば良い？
!
? λが連続かつ範囲が決まってないとき、?
λについての積分が発散してしまい、正規化できない?
→変則事前分布

? 次のような平行移動不変性を持った分布を考える?
(例：正規分布)?
? ※平行移動不変性
? xを定数分移動しても、位置パラメータμを同じだけ移動すれば、?
確率密度の形は変わらない
(2.232)
のときとすると、
(2.233)

? 平行移動不変性を持つ事前分布について考えると、?
積分区間が平行移動しても、その確率は変わらない
!
!
? よって、式(2.235)より定数となる?
(2.234)
(2.235)

? ガウス分布のμの場合、?
σ_0^2→ の極限で無情報事前分布となる
!
!
!
? 事後分布に、事前分布のパラメータが影響しなくなる
(2.140)
(2.141)

2.5 ノンパラメトリック法
? パラメトリック
? 密度関数(モデル)を選んで、パラメータをデータから推定する?
→ モデルがデータを表すのに貧弱だと、予測精度は悪い
? 例) ガウス分布をデータに当てはめて、μ?σ^2を推定した?
→ データが多峰性だと、ガウス分布では捉えられない
? ノンパラメトリック
? 分布の形状に置く仮定が少ない
? 例)多峰性だとか単峰性などの仮定は置かない

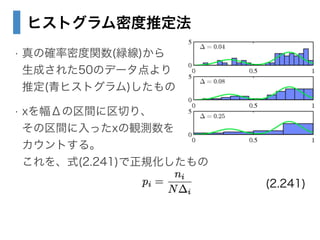
ヒストグラム密度推定法
? 真の確率密度関数(緑線)から?
生成された50のデータ点より?
推定(青ヒストグラム)したもの
? xを幅Δの区間に区切り、?
その区間に入ったxの観測数を?
カウントする。?
これを、式(2.241)で正規化したもの
(2.241)

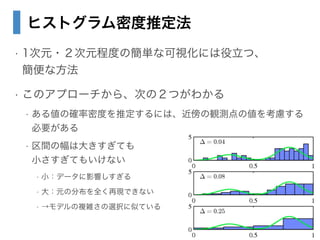
ヒストグラム密度推定法
? 1次元?２次元程度の簡単な可視化には役立つ、?
簡便な方法
? このアプローチから、次の２つがわかる
? ある値の確率密度を推定するには、近傍の観測点の値を考慮する
必要がある
? 区間の幅は大きすぎても?
小さすぎてもいけない
? 小：データに影響しすぎる
? 大：元の分布を全く再現できない
? →モデルの複雑さの選択に似ている

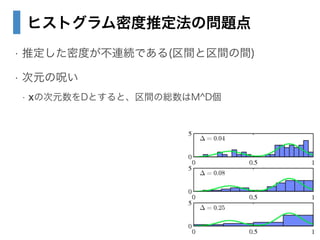
ヒストグラム密度推定法の問題点
? 推定した密度が不連続である(区間と区間の間)
? 次元の呪い
? 虫の次元数を顿とすると、区间の総数は惭镑顿个

2.5.1 カーネル密度推定法
? 未知の確率密度p(x)から得られた観測集合を使って、?
p(x)の値を推定したい
? xを含む小さな領域Rの確率をPとする
!
? N個の観測値が得られたとして、K個の観測値が?
Rに含まれる確率は、二項分布に従う
P =
Z
R
p(x)dx
p(K|N, P) = Bin(K|N, P)
(2.242)
(2.243)

? 二項分布の期待値?分散より、次の関係式が得られる?
?
?
? Nが大きいとき、分散は小さくなり、期待値の関係から
? また、Rが小さく、p(x)がR内で一定だと近似すると
? 以上より、次の密度推定の関係式が得られる
var
?
K
N
=
P(1 P)
N
E
?
K
N
= P
K ' NP
P ' p(x)V
p(x) =
K
NV
(2.244)
(2.245)
(2.246)

? 以上より、次の密度推定の関係式が得られる
!
? 確率密度p(x)を推定するために、KとVを推定する
? Kを固定でVを推定?
→ K近傍密度推定法
? Vを固定でKを推定?
→ カーネル密度推定法
p(x) =
K
NV
(2.246)

? Vを固定し、Kを推定したい
? 確率密度p(x)を求めたい点をx、観測点をx_nとする
? 一辺がhで、xを中心とする小さな超立方体の?
中にある点の総数は
!
? 一辺hの超立方体なので、Vはh^Dとなり、
K =
KX
n=1
k
?
x xn
h
◆
p(x) =
1
N
KX
n=1
1
hD
k
?
x xn
h
◆
(2.248)
(2.249)

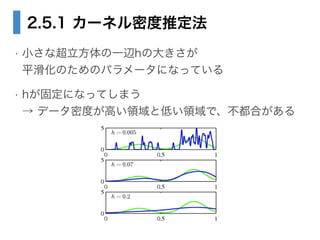
? 小さな超立方体の一辺hの大きさが?
平滑化のためのパラメータになっている
? hが固定になってしまう?
→ データ密度が高い領域と低い領域で、不都合がある

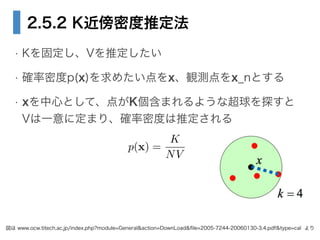
2.5.2 K近傍密度推定法
? Kを固定し、Vを推定したい
? 確率密度p(x)を求めたい点をx、観測点をx_nとする
? xを中心として、点がK個含まれるような超球を探すと?
Vは一意に定まり、確率密度は推定される
図は www.ocw.titech.ac.jp/index.php?module=General&action=DownLoad&?le=2005-7244-20060130-3,4.pdf&type=cal より
p(x) =
K
NV

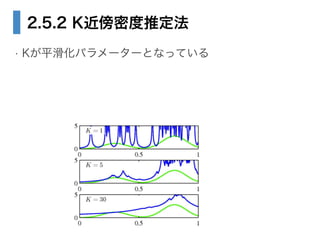
2.5.2 K近傍密度推定法
? Kが平滑化パラメーターとなっている

まとめると…
? カーネル密度推定法
? 領域の体積を固定する
? 一辺の長さがhな超立方体に、観測点xnが何個あるかを求めた
? hが平滑化パラメーター
? K近傍法
? 領域内の、観測点xnの個数を固定する
? 観測点xnがk個になるように、領域を広げた
? kが平滑化パラメーター

K近傍法を使ったクラス分類
? K近傍法とMAP推定を使って、クラス分類を行う
? xのクラスC_kの事後確率を求めたい

? ベイズの定理より、
!
? 確率密度p(x)は、先ほど求めたとおり
!
? 事前分布は、全ての観測点のうちクラスに属する観測点
!
? 尤度は、そのクラスに属する観測点での確率密度より、
p(Ck|x) =
p(x|Ck)p(Ck)
p(x)
p(x) =
K
NV
p(Ck) =
Nk
N
p(x|Ck) =
Kk
NkV

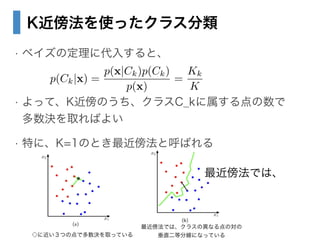
? ベイズの定理に代入すると、
!
? よって、K近傍のうち、クラスC_kに属する点の数で?
多数決を取ればよい
? 特に、K=1のとき最近傍法と呼ばれる
p(Ck|x) =
p(x|Ck)p(Ck)
p(x)
=
Kk
K
◇に近い３つの点で多数決を取っている
最近傍法では、
最近傍法では、クラスの異なる点の対の?
垂直二等分線になっている

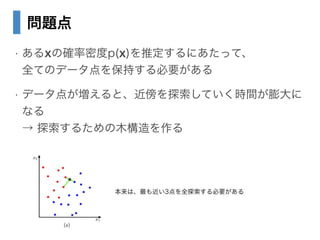
問題点
? あるxの確率密度p(x)を推定するにあたって、?
全てのデータ点を保持する必要がある
? データ点が増えると、近傍を探索していく時間が膨大に
なる?
→ 探索するための木構造を作る
本来は、最も近い3点を全探索する必要がある

狠狠撸

パターン認識と機械学習 ?指数型分布族とノンハ?ラメトリック?

Recommended

More Related Content

What's hot (20)

Similar to パターン認識と機械学習 ?指数型分布族とノンハ?ラメトリック? (20)

パターン認識と機械学習 ?指数型分布族とノンハ?ラメトリック?