More Related Content
What's hot (13)
PDF
ļŗżņØĄņŖżĒŖĖļØ╝ ņĄ£ļŗ© Ļ▒░ļ”¼ ņĢīĻ│Āļ”¼ņ”śņן Ļ│ĄņØś╠²
PPTX
ĻĘĖļלĒöä(Graph)ņÖĆ ĻĘĖļלĒöä ņĢīĻ│Āļ”¼ņ”ś(ļŗ©ņ¢┤ņé¼ļŗżļ”¼ ļ¼ĖņĀ£ ĒĢ┤Ļ▓░)Eunwoo Cho╠²
PPTX
[Gpg1ĻČī ļ░Ģļ»╝ņłś] 4.4 ļ╣ĀļźĖ ņøÉĒåĄ ņĀłļæÉņ▓┤ ĻĄÉņ░© ĒīÉņĀĢMoonLightMS╠²
PDF
3D ßäÅßģźßåĘßäæßģ▓ßäÉßģź ßäĆßģ│ßäģßģóßäæßģĄßå©ßäēßģ│ ßäĆßģĄßäÄßģ®Seung Joon Choi╠²
Viewers also liked (9)
PDF
Build the Virtual Reality Web with A-FrameMozilla VR╠²
PDF
Bringing Virtual Reality to the Web: VR, WebGL and CSS ŌĆō Together At Last!FITC╠²
Similar to ņĀÉ, ņäĀ, ļ®┤ (20)
PPT
[0528 ņäØņ×¼ĒśĖ]Ļ▓īņ×äņØäņ£äĒĢ£ĻĖ░ņ┤łņłśĒĢÖĻ│╝ļ¼╝ļ”¼Jaeho Seok╠²
PPTX
ņäĀĒśĢļīĆņłś 08. ņäĀĒśĢ ļ│ĆĒÖś (Linear Transformation)AHRA CHO╠²
PPTX
ņäĀĒśĢļīĆņłś 09. ļ▓ĪĒä░ņØś ņ¦üĻĄÉņä▒Ļ│╝ Ēł¼ņśüAHRA CHO╠²
PDF
[ņ╗┤Ēō©Ēä░ļ╣äņĀäĻ│╝ ņØĖĻ│Ąņ¦ĆļŖź] 6. ņŚŁņĀäĒīī 2jdo ╠²
PDF
Support Vector Machine Tutorial ĒĢ£ĻĄŁņ¢┤Jungkyu Lee╠²
PDF
[Swift] Data Structure - GraphBill Kim╠²
PDF
─æßģ│─ģßģ®─Č─ąŲ│ßäģąŲóßäåąŲźßäģąŲ│ßå»─ŗßģ▒─ÆßģĪßå½ßäēąŲźßå½─Æßģ¦ßå╝ß░■ąŲóßäēąŲ«ßäÆąŲĪßå©1.2HyeonSeok Choi╠²
PDF
ßäåßģźßäēßģĄßå½ ßäģßģźßäéßģĄßå╝ßäŗßģ│ßå» ßäÆßģóßäćßģ®ßäīßģĪ (ßäēßģ«ßäÆßģĪßå© ßäćßģ®ßäīßģ® ßäīßģĪßäģßģŁ)ssusercdf17c╠²
More from Young-jun Jeong (19)
ņĀÉ, ņäĀ, ļ®┤
- 2. ņĀÉŌĆśņśüņŚŁņØ┤ ņŚåļŖö Ļ▓āŌĆÖ (ņ£ĀĒü┤ļ”¼ļō£)ļ¼╝ņ▓┤ņØś ņ£äņ╣śļź╝ Ēæ£ĒśäĒĢ┤ņŻ╝ļŖö Ļ░£ļģÉĻĘĖļלĒöĮ ņĀüņ£╝ļĪ£ ļÅäĒŖĖļĪ£ Ēæ£ĒśäļÉśļŖö ļ░®ņŗØņØ╝ļ░śņĀüņ£╝ļĪ£ ŌĆśņ¦üĻĄÉņóīĒæ£Ļ│äŌĆÖ ļź╝ ĒåĄĒĢ┤ ļ▓łņŚŁ
- 3. ņóīĒæ£Ļ│äņøÉņĀÉ(O) : ņ£äņ╣śļź╝ ĻĖ░ļ░śĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ĒĢäņÜöņ¦üĻĄÉ ņóīĒæ£ ņŗ£ņŖżĒģ£ĻĄÉņĀ£ņŚÉ ļéśņś© ņóīĒæ£Ļ│äļŖö? ŃģĪŃģĪ;z ņČĢņ£╝ļĪ£ ņé¼ņÜ®ĒĢśļŖö Ļ╣ŖņØ┤Ļ░Æ ļ░®Ē¢źņØś ņ░©ņØ┤ņ╣┤ļ®öļØ╝, ļĀīļŹöļ¦ü ņŚÉņä£ ŌĆśļ¦żņÜ░ŌĆÖ ņżæņÜö!ņ╣┤Ēģīņŗ£ņĢł= ļŹ░ņ╣┤ļź┤ĒŖĖ = ņ¦üĻĄÉ ņóīĒæ£Ļ│äļĪ£ ņØ┤ĒĢ┤
- 4. ņĢäĒĢĆ Ļ│ĄĻ░äņØ┤ļ¤¼ĒĢ£ ņóīĒæ£Ļ│äņØś ņĀĢņØśļź╝ ņ£äĒĢ┤ ļ▓ĪĒä░ņØś ņøÉļ”¼ļź╝ ņØ┤ņÜ®ĻĘĖļ¤¼ĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņĀÉ ŌĆō ļ▓ĪĒä░ Ļ┤ĆĻ│äļź╝ ņĀĢņØśĒĢśļŖö ļ░®ļ▓ĢņØ┤ ĒĢäņÜöņĀÉļōżņØś ņ¦æĒĢ® WņÖĆ ļ▓ĪĒä░ Ļ│ĄĻ░ä VļĪ£ ĻĄ¼ņä▒.ļ▓ĪĒä░ v = ņĀÉQ ŌĆō ņĀÉP (Q, PļŖö WņĢł)
- 5. ņĢäĒĢĆ Ļ│ĄĻ░äņĢäĒĢĆ Ļ│ĄĻ░äņŚÉņä£ Ļ│ĀņĀĢņĀÉ(O)ņÖĆ ĻĖ░ņĀĆ ļ▓ĪĒä░ļōżņØś ņĪ░ĒĢ®ņ£╝ļĪ£ ŌĆśņóīĒæ£ ĒöäļĀłņ×äŌĆÖ ņØä ĻĄ¼ņä▒ĒĢ£ļŗż.ĻĘĖļ¤¼ļéś, ņØ┤ļŖö ĻĖ░ņĀĆ ļ▓ĪĒä░Ļ░ä Ļ┤ĆĻ│äĻ░Ć ŌĆśņ¦üĻĄÉŌĆÖ ĒĢ£ļŗżļŖö ņØśļ»ĖļŖö ņĢäļŗłļŗż. ļ¼╝ļ”¼ņĀü ĻĖ░ĒĢśĒĢÖņØä ņóĆļŹö ņČöņāüņĀüņ£╝ļĪ£ Ēæ£Ēśä ĒĢĀ ņłś ņ׳Ļ▓ī ĒĢśĻĖ░ ņ£äĒĢ┤ ŌĆśņ¦üĻĄÉņóīĒæ£ ĒöäļĀłņ×äŌĆÖ ņØä ņé¼ņÜ®ĒĢ£ļŗż.ņé╝Ļ░üĒĢ©ņłśļź╝ ņØ┤ņÜ®ĒĢ£ ŌĆśņ£ĀĒü┤ļ”¼ļō£Ļ▒░ļ”¼ŌĆÖ
- 6. ņĢäĒĢĆ Ļ▓░ĒĢ®ņĢäĒĢĆ Ļ│ĄĻ░ä ņĀĢņØś ņ┤łĻĖ░ņŚÉ ņŚ░ņé░ ĻĘ£ņ╣ÖņØĆ ŌĆś-ŌĆÖ ļź╝ ņØ┤ņÜ®ĒĢ┤ņä£ ļ▓ĪĒä░ļź╝ ĻĄ¼ĒĢśļŖö ļ░®ļ▓ĢņØ┤ ņ׳ņŚłļŗż.ņĀÉĻ│╝ ĻĖ░ņĀĆļ▓ĪĒä░ņØś Ļ┤ĆĻ│äņŚÉņä£ ņĀÉļōżņØś Ļ│äņłś ĒĢ®ņØ┤ 1ļĪ£ ņĀ£ĒĢ£ļÉ£ ņé¼ĒĢŁņŚÉņä£ ĒĢ£ ņĀÉĻ│╝ ļ▓ĪĒä░ļōżņØś ŌĆśņäĀĒśĢĻ▓░ĒĢ®ŌĆÖ ņ£╝ļĪ£ ļīĆņ▓┤ ņĀĢņØśĻ░Ć Ļ░ĆļŖźĒĢśļŗżļŖö Ļ▓ā.ņØ┤ļŖö ņäĀĒśĢĻ▓░ĒĢ®ņØä ĒåĄĒĢ┤ Ļ│ĄĻ░äņØä ņāØņä▒ĒĢśļŖö Ļ▓ā ņ▓śļ¤╝ņĢäĒĢĆ Ļ▓░ĒĢ®ņØä ĒåĄĒĢ┤ ņĢäĒĢĆ Ļ│ĄĻ░äņØä ņāØņä▒.
- 7. ņĀÉ ĻĄ¼Ēśäņ¦üĻĄÉ ņóīĒæ£ ĒöäļĀłņ×äņŚÉņä£ ļ▓ĪĒä░ļź╝ ņé¼ņÜ®ĒĢĀļĢī, ņĢäĒĢĆĻ│ĄĻ░äņŚÉņä£ ņĀÉOĻ░Ć ņøÉņĀÉņØ╝ļĢīņÖĆ Ļ░ÖņØ┤ ņĀÉņ£╝ļĪ£ ņåÉņēĮĻ▓ī ļ│ĆĒÖśņØ┤ Ļ░ĆļŖźĒĢ┤ ņ¦äļŗż.ļ¦ÄņØĆ ņłśĒĢÖ ļØ╝ņØ┤ļĖīļ¤¼ļ”¼ ļōżņØ┤ ņĀÉ Ēü┤ļלņŖżļź╝ ļ▓ĪĒä░ Ēü┤ļלņŖż ļĪ£ ņØ┤ņÜ®ĒĢ┤ņä£ ĻĄ¼ĒśäĒĢ£ļŗż.4ĒŖ£ĒöīņØäņŹ╝ņØäļĢīņŚÉļÅä ļ¦łņ¦Ćļ¦ē ņäĖĒŖĖ ņāüņłśĻ░ÆņŚÉ ļö░ļØ╝ ņĀÉņØĖņ¦Ć ļ▓ĪĒä░ņØĖņ¦Ć ĻĄ¼ļČäĒĢ£ļŗż.ex) OpenGL light ĒĢ©ņłś
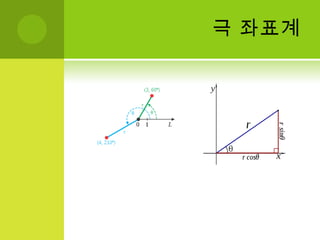
- 9. ĻĘ╣ ņóīĒæ£Ļ│ärņÖĆ ╬ĖļŖö ņé╝Ļ░üĒĢ©ņłśļź╝ ņØ┤ņÜ®ĒĢ┤ ļŹ░ņ╣┤ļź┤ĒŖĖ ņóīĒæ£ņØś xņÖĆ yļĪ£ ļ│ĆĒÖśĒĢĀ ņłś ņ׳ļŗż.x= rcos╬Ėy= rsin╬ĖļŹ░ņ╣┤ļź┤ĒŖĖ ņóīĒæ£ņØś xņÖĆ yļŖö ĻĘ╣ņóīĒæ£ņØś rļĪ£ ļ│ĆĒÖśĒĢĀ ņłś ņ׳ļŗż.r2= x2+ y2(Ēö╝ĒāĆĻ│ĀļØ╝ņŖż ņĀĢļ”¼ ņé¼ņÜ®)╬Ėļź╝ ņĀĢņØśĒĢĀ ļĢīļŖö ļŗżņØīĻ│╝ Ļ░ÖņØĆ ņé¼ĒĢŁņØä Ļ│ĀļĀżĒĢ┤ņĢ╝ ĒĢ£ļŗż.- r= 0 ņØ╝ ļĢīļŖö ╬ĖļŖö ņ×äņØśņØś ņŗżņłśĻ░Ć ļÉĀ ņłś ņ׳ļŗż.rŌēĀ 0 ņØ╝ ļĢīļŖö Ēæ£ĒśäņØś ņ£ĀņØ╝ņä▒ņØä ņ£äĒĢśņŚ¼ Ēü¼ĻĖ░Ļ░Ć 2ŽĆļ│┤ļŗż ņ×æņØĆ ĻĄ¼Ļ░äņ£╝ļĪ£ ĒĢ£ņĀĢĒĢ£ļŗż. ļ│┤ĒåĄņØĆ [0, 2ŽĆ) ļéś (ŌłÆŽĆ, ŽĆ]Ļ░Ć ņé¼ņÜ®ļÉ£ļŗż.
- 10. ņŗżņāØĒÖ£ņŚÉņä£ļŖö ļ░░ļéś ļ╣äĒ¢ēĻĖ░ņØś ĒĢŁĒ¢ēņóīĒæ£ļź╝ Ļ│äņé░ĒĢ┤ ņżä ļĢī ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŗż. (Ļ▓īņ×äņāüņŚÉņä£ļŖö ņóīĒæ£ ļ│ĆĒÖśĒĢśĻĖ░ ĻĘĆņ░«ņ£╝ļ»ĆļĪ£ ņ¦üĻĄÉņóīĒæ£Ļ│äļĪ£ ņé¼ņÜ®)r(╬Ė) = a + b╬Ė
- 12. ņäĀy = mx + bņäĀļČäļ░śņ¦üņäĀ (ņ╣┤ļ®öļØ╝ ņ£äņ╣śņÖĆ ņŗ£ņĢ╝ļ░®Ē¢ź ļō▒)
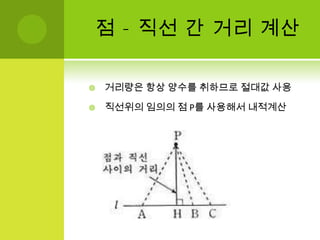
- 14. ņĀÉ ŌĆō ņ¦üņäĀ Ļ░ä Ļ▒░ļ”¼ Ļ│äņé░Ļ▒░ļ”¼ļ¤ēņØĆ ĒĢŁņāü ņ¢æņłśļź╝ ņĘ©ĒĢśļ»ĆļĪ£ ņĀłļīĆĻ░Æ ņé¼ņÜ®ņ¦üņäĀņ£äņØś ņ×äņØśņØś ņĀÉ Pļź╝ ņé¼ņÜ®ĒĢ┤ņä£ ļé┤ņĀüĻ│äņé░

![[Devrookie]ĻĮØļ¦żļŗłņĢäņĀÉ, ņäĀ, ļ®┤](https://image.slidesharecdn.com/random-110823094607-phpapp02/85/-1-320.jpg)






![ĻĘ╣ ņóīĒæ£Ļ│ärņÖĆ ╬ĖļŖö ņé╝Ļ░üĒĢ©ņłśļź╝ ņØ┤ņÜ®ĒĢ┤ ļŹ░ņ╣┤ļź┤ĒŖĖ ņóīĒæ£ņØś xņÖĆ yļĪ£ ļ│ĆĒÖśĒĢĀ ņłś ņ׳ļŗż.x= rcos╬Ėy= rsin╬ĖļŹ░ņ╣┤ļź┤ĒŖĖ ņóīĒæ£ņØś xņÖĆ yļŖö ĻĘ╣ņóīĒæ£ņØś rļĪ£ ļ│ĆĒÖśĒĢĀ ņłś ņ׳ļŗż.r2= x2+ y2(Ēö╝ĒāĆĻ│ĀļØ╝ņŖż ņĀĢļ”¼ ņé¼ņÜ®)╬Ėļź╝ ņĀĢņØśĒĢĀ ļĢīļŖö ļŗżņØīĻ│╝ Ļ░ÖņØĆ ņé¼ĒĢŁņØä Ļ│ĀļĀżĒĢ┤ņĢ╝ ĒĢ£ļŗż.- r= 0 ņØ╝ ļĢīļŖö ╬ĖļŖö ņ×äņØśņØś ņŗżņłśĻ░Ć ļÉĀ ņłś ņ׳ļŗż.rŌēĀ 0 ņØ╝ ļĢīļŖö Ēæ£ĒśäņØś ņ£ĀņØ╝ņä▒ņØä ņ£äĒĢśņŚ¼ Ēü¼ĻĖ░Ļ░Ć 2ŽĆļ│┤ļŗż ņ×æņØĆ ĻĄ¼Ļ░äņ£╝ļĪ£ ĒĢ£ņĀĢĒĢ£ļŗż. ļ│┤ĒåĄņØĆ [0, 2ŽĆ) ļéś (ŌłÆŽĆ, ŽĆ]Ļ░Ć ņé¼ņÜ®ļÉ£ļŗż.](https://image.slidesharecdn.com/random-110823094607-phpapp02/85/-9-320.jpg)