Termodinamika
- 1. Termodinamika Termodinamika (bahasa Yunani: thermos = 'panas' and dynamic = 'perubahan') adalah fisika energi, panas, kerja, entropi dan kespontanan proses. Termodinamika berhubungan dekat dengan mekanika statistik dimana banyak hubungan termodinamika berasal. Termodinamika adalah kajian tentang kalor (panas) yang berpindah. Dalam termodinamika kamu akan banyak membahas tentang sistem dan lingkungan. Kumpulan benda-benda yang sedang ditinjau disebut sistem, sedangkan semua yang berada di sekeliling (di luar) sistem disebut lingkungan
- 2. Hukum termodinamika 1 Merupakan pernyataan dari kekekalan energi : energi tidak dapat diciptakan atau dimusnahkan, tapi energi dapat diubah dari suatu bentuk ke bentuk lain. Dengan kata lain, total energi dari suatu sistem dan lingkungan disekitarnya (merupakan sistem terisolasi) adalah tetap dalam tiap proses Pernyataan ini berdasarkan kenyataan bahwa berbagai bentuk energi adalah sama dan jika satu jenis terbentuk, sejumlah yang sama dari jenis lain akan hilang
- 3. TERMODINAMIKA ’ü▒ PROSES-PROSES TERMODINAMIKA ’āś Proses Isobarik (1) ’é¦ Tekanan konstan ’āś Proses Isotermis (2) ’é¦ Temperatur kontan ’āś Proses Adiabatis (3) ’é¦ Tidak ada kalor yang hilang ’āśProses Isokorik (4) ’é¦ Volume konstan
- 4. HUKUM TERMODINAMIKA PERTAMA Selisih antara Kalor yang diberikan dan kerja yang dilakukan selalu sama untuk setiap proses f i DU = Q-W DU = U - U Ui = Energi dalam mula-mula Uf = Energi dalam akhir DU = Perubahan energi dalam sistem Q = Panas yang diberikan pada sistem W = Kerja yang dilakukan oleh sistem
- 5. ’āśPROSES ISOKHORIK ’é¦ KERJA : V f = ├▓ W pdV V i = ┬« = V V W 0 f i ’é¦ KALOR Q nC T nC (T T ) V V f i = D = - ’é¦ PERUBAHAN ENERGI DALAM : U Q W U nC T VD = - ┬« D = D n = Jumlah mol CV = Kapasitas panas volume konstan
- 6. ’āśPROSES ISOBARIK ’é¦ KERJA : f = ├▓ = W pdV p kons tan W p(V V ) p V f i V V i = - = D ’é¦ KALOR Q nC T nC (T T ) P P f i = D = - ’é¦ PERUBAHAN ENERGI DALAM : D = - ┬« D = D - D U Q W U nC T p V P = ┬« D = D pV nRT p V nR T = + ┬« D = D - D = D C C R U nC T nR T nC T P V P V R = Konstanta gas universal = 8.31 J/mol.K CP = Kapasitas panas tekanan konstan
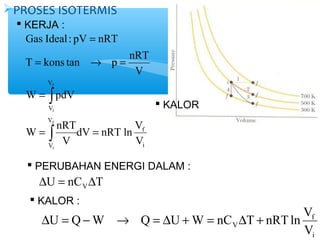
- 7. ’āśPROSES ISOTERMIS ’é¦ KERJA : T = kons tan ┬« p = nRT f ├▓ W pdV i = = dV nRT ln V V f i V V V V V W nRT V Gas Ideal : pV nRT f i = = ├▓ ’é¦ KALOR ’é¦ PERUBAHAN ENERGI DALAM : DU = Q-W ┬« Q = DU +W = nC DT + nRTln V f V V i U nC T VD = D ’é¦ KALOR :
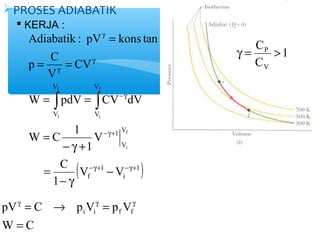
- 8. ’āśPROSES ADIABATIK ’é¦ KERJA : Adiabatik : pV kons tan CV p C = = V -g g = = W pdV CV dV -g+ ( 1 1 ) f i V V 1 V V V V V V 1 C V 1 W C 1 f i f i f i -g+ -g+ g g - - g = - g + = = ├▓ ├▓ 1 C g = P > C V g = ┬« g = g pV C p V p Vi i f f = W C
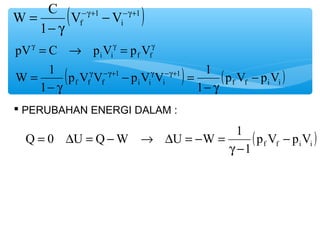
- 9. W C -g+ - -g+ ( V 1 V 1 ) f i g g g pV C p V p V i i f f p V V p V V 1 ( 1 1 ) ( ) f f f i i i f f i i W 1 ’é¦ PERUBAHAN ENERGI DALAM : Q 0 U Q W U W 1 - ( f f i i ) p V p V 1 g - = D = - ┬« D = - = p V p V 1 1 - - g - = - g = = ┬« = g -g+ g -g+ 1 - g =
- 10. W Q DU Isokhorik 0 Isobarik nC T VD nC T VD p(V V ) f i - nC T VnC T D PD Isotermis 0 nRTln V f V nRTln V Adiabatik 0 nC T VD DU = Q-W 1 f V 1 ( ) i i f f p V p V 1 1 - - g
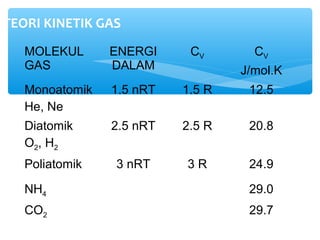
- 11. TEORI KINETIK GAS MOLEKUL GAS ENERGI DALAM CV CV J/mol.K Monoatomik He, Ne 1.5 nRT 1.5 R 12.5 Diatomik O2, H2 2.5 nRT 2.5 R 20.8 Poliatomik 3 nRT 3 R 24.9 NH4 29.0 CO2 29.7
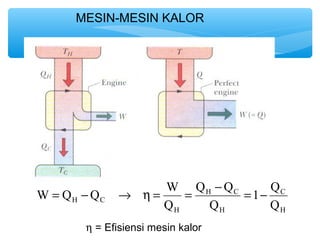
- 12. MESIN-MESIN KALOR C H W = Q -Q ® h = W = Q - Q H C = - H C Q H H 1 Q Q Q h = Efisiensi mesin kalor
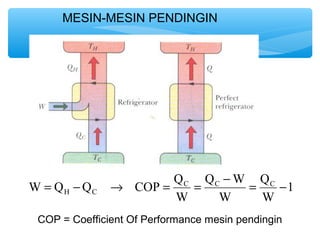
- 13. MESIN-MESIN PENDINGIN 1 H C = - ® = = - = - W Q Q COP QC Q C C W Q W W W COP = Coefficient Of Performance mesin pendingin
- 14. Contoh Soal No. 1 Pada gambar di bawah ini ditunjukkan siklus proses-proses yang terjadi pada mesin diesel (gasoline internal combustion engine). a). Tentukan tekanan dan temperatur pada setiap keadaan (titik) dalam p1, V1 dan perbandingan panas jenis g. b). Hitung efisiensi dari mesin diesel ini Jawab : p V nRT T p1V1 1 1 1 1 a). = ® = nR p , V , p1V1 1 1 Titik 1 : nR
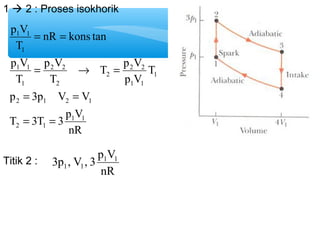
- 15. 1 ’āĀ 2 : Proses isokhorik = = p V p V 1 1 1 p V = 2 2 ┬« = 1 1 = = p 3p V V 2 1 2 1 T 3T 3 p V nR T T p V 2 2 p V T T nR kons tan T 1 1 2 1 1 1 1 2 2 1 = = Titik 2 : 3p , V , 3 p1V1 nR 1 1
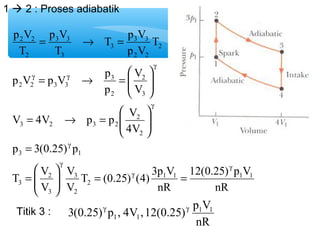
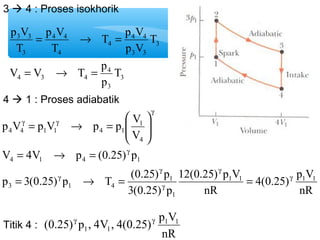
- 16. 1 ’āĀ 2 : Proses adiabatik 12(0.25) p V nR T p V 3 3 V 2 V p V p V = 3 3 ┬« = 2 2 p V p V p 3 ├” V 4V p p V p 3(0.25) p 3 1 2 g ├Č ├Č T (0.25) (4) 3p V V nR V ├” = T V 2 V 4V p T p V T T 1 1 1 1 2 3 2 3 3 2 3 2 3 2 3 2 2 2 3 3 2 2 2 3 3 2 g g g g g g g ├Č = = ├Ę ├Ę├Ė ├¦ ├¦├© = ├Ę ├Ę├Ė ├¦ ├¦├© ├” = ┬« = ├Ę ├Ę├Ė ├¦ ├¦├© = ┬« = Titik 3 : 3(0.25) p , 4V ,12(0.25) p1V1 nR g g 1 1
- 17. 3 ’āĀ 4 : Proses isokhorik T p V = ┬« = 3 4 3 p V 4 4 p V 3 3 V V T p 4 3 4 3 4 4 3 3 4 4 3 T p T p V T T = ┬« = 4 ’āĀ 1 : Proses adiabatik ├¦ ├¦├© ├” p V p V p p V 1 V = ┬« = = ┬« = V 4V p (0.25) p 4 1 4 1 g ├Č ├Ę ├Ę├Ė p 3(0.25) p T (0.25) p Titik 4 : 12(0.25) p V 1 (0.25) p , 4V , 4(0.25) p1V1 nR g g 1 1 4(0.25) p V nR nR 3(0.25) p 1 1 1 1 1 3 1 4 4 4 4 1 1 4 1 g g g g g g g g = ┬« = =
- 18. b). = = Q Q 0 41 23 = - = - Q nC (T T ) Q nC (T T ) 12 V 2 1 34 V 4 3 Titik 1: p , V , p1V1 nR 1 1 Titik 2 : 3p , V , 3 p1V1 nR Titik 3: 3(0.25) p , 4V ,12(0.25) p1V1 nR g g 1 1 Titik 4 : (0.25) p , 4V , 4(0.25) p1V1 nR g g 1 1 1 1 ] 8(0.25) C p V R ] 2C p V = - = - = 12(0.25) p V nR p V Q nC (T T ) nC [3 p V Q nC (T T ) nC [4(0.25) p V nR R nR nR 1 1 V 1 1 1 1 34 V 4 3 V 1 1 V 1 1 1 1 12 V 2 1 V = - = g - g = - g
- 19. W W 0 W 1 12 34 23 3 3 2 2 - (p V p V ) W 1 1 (p V p V ) 1 41 1 1 4 4 - g = - - g = = = Titik 1: p , V , p1V1 Titik 2 : 3p , V , 3 p1V1 Titik 3: 3(0.25) g p , 4V ,12(0.25) g p1V1 Titik 4 : (0.25) g p , 4V , 3(0.25) g p1V1 = g g 23 3 3 2 2 1 1 1 1 - [12(0.25) 3] W 1 [3(0.25) p 4V 3p V ] p V 1 1 1 (p V p V ) 1 1 1 - g - = - g - = - g nR 1 1 nR 1 1 nR 1 1 nR 1 1 [1 4(0.25) ] W 1 [p V (0.25) p 4V ] p V 1 1 1 (p V p V ) 1 41 1 1 4 4 1 1 1 1 1 1 g - g - g - = - g - = - g = W W W W W p1V1 [2 8(0.25) ] 1 total 12 23 34 41 - g g - = + + + =
- 20. ] 8(0.25) C p V R ] 2C p V = - = - = 12(0.25) p V nR p V Q nC (T T ) nC [3 p V Q nC (T T ) nC [4(0.25) p V nR R nR nR 1 1 V 1 1 1 1 34 V 4 3 V 1 1 V 1 1 1 1 12 V 2 1 V = - = g - g = - g W W W W W p1V1 [2 8(0.25) ] 1 total 12 23 34 41 - g g - = + + + = Q Q 2C p1V1 12 H V = = R Q Q 8(0.25) C p1V1 34 C V R = = - g ( 1) [2 8(0.25) ] R 1 1 1 V [2 8(0.25) ] 1 [2 8(0.25) ] 1 2C p V C C p V C W [2 8(0.25) ] 1 [2 8(0.25) ] C 1 R p V Q V V 1 1 H g g g g g g - = - g - = - - g - h = - - g - = - h = = g - g =1.4 ® h = 2 -8(0.25)1.4 = 0.85
- 21. Contoh Soal No. 2 Pada gambar di bawah ini ditunjukkan siklus mesin kalor yang disebut mesin kalor Carnot. Mesin ini bekerja pada dua temperatur TH dan TC. Nyatakan efisiensinya dalam TH dan TC Jawab : a ’āĀ b : Isotermis W = nRT ln V U 0 Q nRT ln V b a b a H H ab H V V D = ┬« = c ’āĀ d : Isotermis W = nRT ln V U 0 Q nRT ln V d c d c C C cd C V V D = ┬« =
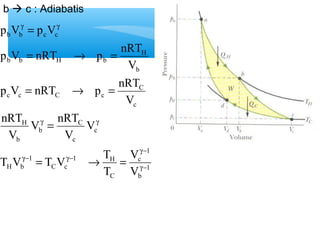
- 22. b ’āĀ c : Adiabatis g g p V nRT p nRT V = ┬« = p V nRT p nRT g- 1 c V 1 b = ┬« = V nRT nRT g g = T V T V T 1 H C b b c c C c 1 H b c c C b b H c C c c C c b H b b H b V T V V V V p V p V g- g- g- = ┬« = =
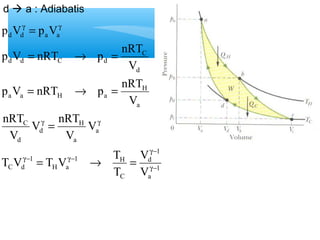
- 23. g- 1 d d ’āĀ a : Adiabatis g g p V nRT p nRT V = ┬« = p V nRT p nRT V 1 a = ┬« = V nRT nRT g g = T V T V T 1 H C d d a a H a 1 C d a a H d d C a H a a H a d C d d C d V T V V V V p V p V g- g- g- = ┬« = =
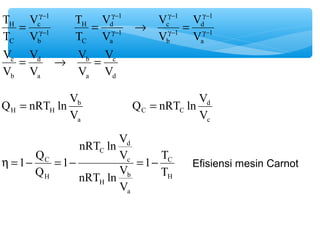
- 24. g- 1 d V g- g- = = ® = g- V c d T H V b a 1 c V V d a T H V c b 1 d V 1 a 1 c V 1 b 1 a C 1 b C V V V V V V V T V T = ® = g- g- g- g- Q = nRT ln V b H H V a Q = nRT ln V d C C V c h =1- Q = - = 1 - T C Efisiensi mesin Carnot H nRT ln V d V nRT ln V b a H c C C H T V 1 Q
- 25. HUKUM TERMODINAMIKA KEDUA * Tidak ada mesin kalor yang mempunyai efisiensi lebih besar dari mesin kalor Carnot * Tidak ada mesin pendingin yang mempunyai COP lebih besar dari mesin pendingin Carnot C 1 T C T T H C C C H COP T T - h = - =
- 26. Contoh Soal No. 3 Sebuah turbin pada suatu steam power plant mengambil uap air dari boiler pada temperatur 520oC and membuangnya ke condenser pada temperatur 100oC. Tentukan efisiensi maksimumnya. Jawab : Efisiensi maksimum = efisiensi Carnot h = - C = - = = 0.53 53% 1 373 793 1 T T H Karena gesekan, turbulensi dan kehilangan panas Efisiensi aktual dari turbin disekitar 40 % Efisiensi teoritis dari mobil adalah disekitar 56 %. Eefisiensi aktualnya hanya disekitar 25 %
- 27. Contoh Soal No. 4 Seorang inventor menyatakan bahwa ia telah mengembangkan sebuah mesin kalor yang selama selang waktu tertentu mengambil panas sebesar 110 MJ pada temperatur 415 K dan membuang panas hanya sebesar 50 MJ pada temperatur 212K sambil menghasilkan kerja sebesar 16.7kwh. Apakah saudara akan menginvestasikan uang saudara ? Jawab : 1 212 1 T h = = = 0.55 0.49 16.7(360) 110x10 W Q 6 H C h = - = - = 415 C T H Efisiensinya > Efisiensi mesin Carnot ’āĀ Jangan investasi
- 28. Contoh Soal No. 5 Sebuah mobil yang efisiensinya 22 % beroperasi pada 95 c/s dan melakukan kerja dengan daya sebesar 120 hp. a). Berapa kerja yang dilakukan mesin tersebut setiap siklus ? b). Berapa bayak kalor yang diserap dari reservoir setiap siklus ? c). Berapa banyak kalor yang terbuang setiap siklus Jawab : 942 J Kerja setiap siklus : W = 120(746) = 95 a).
- 29. b). 4282 J Q W 942 0.22 W Q H H = = h h = ® = c). Q Q W 4282 942 3340 J C H = - = - =





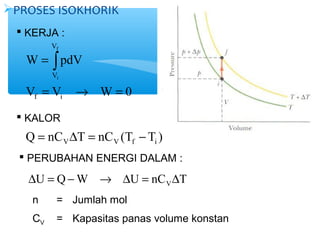



![b).
= =
Q Q 0
41 23
= - = -
Q nC (T T ) Q nC (T T )
12 V 2 1 34 V 4 3
Titik 1: p , V , p1V1
nR
1 1
Titik 2 : 3p , V , 3 p1V1
nR
Titik 3: 3(0.25) p , 4V ,12(0.25) p1V1
nR
g g
1 1
Titik 4 : (0.25) p , 4V , 4(0.25) p1V1
nR
g g
1 1
1 1
] 8(0.25) C p V
R
] 2C p V
= - = - =
12(0.25) p V
nR
p V
Q nC (T T ) nC [3 p V
Q nC (T T ) nC [4(0.25) p V
nR
R
nR
nR
1 1
V
1 1 1 1
34 V 4 3 V
1 1
V
1 1 1 1
12 V 2 1 V
= - = g - g = - g](https://image.slidesharecdn.com/presentasitermodinamika-141122020757-conversion-gate02/85/Termodinamika-18-320.jpg)
![W W 0 W 1
12 34 23 3 3 2 2
-
(p V p V )
W 1
1
(p V p V )
1
41 1 1 4 4
- g
=
-
- g
= = =
Titik 1: p , V , p1V1
Titik 2 : 3p , V , 3 p1V1
Titik 3: 3(0.25) g p , 4V ,12(0.25) g
p1V1
Titik 4 : (0.25) g p , 4V , 3(0.25) g
p1V1
= g g
23 3 3 2 2 1 1 1 1 -
[12(0.25) 3]
W 1 [3(0.25) p 4V 3p V ] p V
1 1
1
(p V p V ) 1
1
1
- g
- =
- g
- =
- g
nR
1 1
nR
1 1
nR
1 1
nR
1 1
[1 4(0.25) ]
W 1 [p V (0.25) p 4V ] p V
1 1
1
(p V p V ) 1
41 1 1 4 4 1 1 1 1
1
1
g - g
- g
- =
- g
- =
- g
=
W W W W W p1V1
[2 8(0.25) ]
1
total 12 23 34 41
- g
g -
= + + + =](https://image.slidesharecdn.com/presentasitermodinamika-141122020757-conversion-gate02/85/Termodinamika-19-320.jpg)
![] 8(0.25) C p V
R
] 2C p V
= - = - =
12(0.25) p V
nR
p V
Q nC (T T ) nC [3 p V
Q nC (T T ) nC [4(0.25) p V
nR
R
nR
nR
1 1
V
1 1 1 1
34 V 4 3 V
1 1
V
1 1 1 1
12 V 2 1 V
= - = g - g = - g
W W W W W p1V1
[2 8(0.25) ]
1
total 12 23 34 41
- g
g -
= + + + =
Q Q 2C p1V1
12 H V = =
R
Q Q 8(0.25) C p1V1
34 C V
R
= = - g
( 1) [2 8(0.25) ]
R
1
1 1 V
[2 8(0.25) ]
1
[2 8(0.25) ]
1
2C p V
C C
p V
C
W
[2 8(0.25) ]
1
[2 8(0.25) ]
C
1
R
p V
Q
V
V
1 1
H
g
g g
g
g
g - = -
g -
= -
-
g -
h = -
-
g -
=
-
h = = g -
g =1.4 ® h = 2 -8(0.25)1.4 = 0.85](https://image.slidesharecdn.com/presentasitermodinamika-141122020757-conversion-gate02/85/Termodinamika-20-320.jpg)