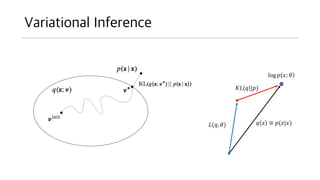
Variational inference intro. (korean ver.)
- 2. Information ? ????? ????. ? ??? ??(distribution)? ? ? ??? ??? ??? ??? ?? ?. ? ?? ?? ??? ???? ??? ?? ??? ??. ? ?? ???? ???? ?? ? ???? ???? ??. ? Variational ?? ?? ???? ?? ???? ??? ???? ???.
- 3. Basic Theory
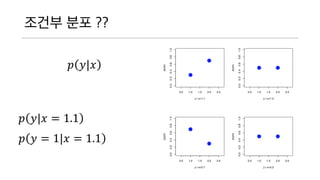
- 4. Probability ? Ī░???? ? ?? ?? ??? 1/6 ??Ī▒ ? ??? ????? ?? ? Ī░??? ???? 10?? ??? ?? ? ?? ?? ??? ?? 1/6 ?? ?? ??? XX?.Ī▒ ? ??? ????? ?? ? Ī░?? ??? ??? ??? 0.000000000000000001 ??Ī▒ ? ??? ???? ?? ??? ?? ?? ?? ? Ī░???? ??? ??? ??? ??? ??? ??? ?? ??? ??? ??? ??.Ī▒ ? ??? ?? ?? ?(?)
- 5. Probability (ContĪ»d) ? ?? ??? ?? ??? ???? ????? ? ????? ?? ?? ?? ?? ??? ??? ?? ??? ??? ? ?? ? ??. ? ??? ???. <= ? ??? ???? ??. ? ?? ??? ???? ?? ?? ?? ??. ? ?? ??? ??? ??? Ī░??Ī▒ ? ?? ?? ? ?? ?? ?? ?? (??? ???) ? http://cs229.stanford.edu/section/cs229-prob.pdf ?(?)
- 6. Probability (ContĪ»d) ? ?? ?? (Probability function ??) ? ?? ??? ???? ?? ?? ?? ??. ? ?? ?? ??? ?? ??. ? ?? 1??? (PMF) ??? 1 (PDF). ? ?? ?? ?? 0?? ?? ??. ? ?? ? ???? ??? ??? ?? ??? ??? ?. ? PMF? PDF? ??? ?? ??? ??. ? ?? Ī▌ 0 ? ? ? ?? =1 R.V PMF ? ?? Ī▌ 0 ?Ī▐ Ī▐ ? ?? = 1 PDF
- 7. ?? ??? (2?? ?? ?? ??) ? ?,? ?, ? ? ?,? ?, ? = ? ?(?)? ?(?) ? R.V. ? ??? ?? ? ?,? ? | ? ???? x? y ? ?? ???? ?? y ? ????? ? ??? ? ??. ? ?|? = ? ? ? ?(?) ?(?) ? ? = 3|? ? ? = 3|? = 0 ? ? = 3|? = 1?? ?|? = 1
- 8. ??? ?? ?? ? ?|? ? ?|? = 1.1 ? ? = 1|? = 1.1
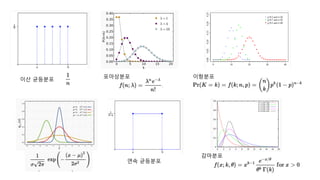
- 9. Probability Distribution with Parameter ? ??(distribution)? ?? ?? ?? ??? ?? ???? ?? ?? ??. ? ?? ???? ????? ?? ?? ??? ????? ????? ??. ? ????(parameter)? ?? ?? ???? ?? ????? ?? ? ?? ??, ?? ?? ??? ??? ?? ?? ? ??. (???? ????) ? Ex) ????, ?????, ????, ????, ????, ?????? ?? ?(?; ?)
- 10. ?? ???? ????? ???? ?? ???? ????
- 11. MLE (Maximum Likelihood Estimation) ? = ? ?; ? [??] ?? ???? ?? ????? ????. ????? ?? ??? ?? ?? ??? likelihood ?? ??? ???. ? ?; ? ? ?? ?; ? ?? ?? ?? p(x)??? ??? ??????, ? ??? ???? ??? L ??? ????. ?? ? ?; ? = ?????? ? ?(?; ?)
- 12. ??? ???? ? ?? ? Frequentist ? ?? : ??? ???? ?? ? ????? ?? ???? ??? ? ? ? (unknown but fixed) ? ?? ??? ?? ?? ??? ?? ? ??. ? Bayesian ? ?? : ??? ?? ? ????? ?? ??? ? ? ??. ? ??? ???? ?? ??? ??? ??. ? ? = ?????? ? ?(?; ?) ? ? = ?????? ? ?(?|?) ?? ??
- 13. Expectation ? ?? ?? ?? ???(??)?? ???? ??? ??. (? ? [?]) ? ??? ?? ??? ?? ??? ?? ???. ? ?? ????? ???? ??? ????? ????? ??. ? ?? ??? ???? ????? ? ? [?] = ?? ? ?? , ? ? [?] = ? ? ? ? ??
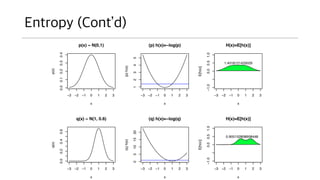
- 15. Information ? Shannon ??? ??? ????. ? ???? ????? ?? Ī░??Ī▒? ??? ???. ? ?? ???? ???? ??? ?? ??? ?? ???? ????. ?? ?? ?? ?? ?.. ? ?? ??? ?? ?? ??? ???? ????? ?. ? ??? ?? ???? ?? ???? ???? ??? ???. ? ??? ??? ???? ??? ??? ? ?? ?? ??? ??. ? ?? ?? ??? ???? ?? ??? ??? ??? ???? ???, ??? ??? ?? ???? ?? ?? ? ? ??? ??. ? ??? ??? ?? ? ? ??? ?? ??? ??? ?? ?? ???? ??. ? ? = ? log ?(?)
- 16. Information (ContĪ»d) ? ?? 1?? ?? ??? (?? 6?) ? ?? 5?? ?? ??? (?? 3?) ? ??? ??? 1? ?? ??? ?? ??? ? ? = ? log2 1 8,145,060 ? 23 ? ? = ? log2 1 45 ? 5.5 ? ? = ? log2 1 6 ? 2.6
- 17. Entropy ? Entropy?? ? ??? ?(system)? ??? ?? ???. ? ??? ????? ? ?? ??. ????? ? ?? ?? ???ĪŁ ? ???? ?? ?? ???? Ī░? vs ?Ī▒ ??? ??? ?? ? ??. ? ??? ??? ?? ?? ??? ??? ??. ? Entropy ? ? ???? ??? 2? ??? ???? ??, ? ??? ???? ???? ?? ??? bit ? ??? ??? ???? ? ??. ? ??? ?? ???? ??. ?? ??? ?? ?. ? ? = ? ? ? ? log2 ?(?) E ? = ? ? ? ? ?? E ? = ? ? ?(?)
- 19. KL-divergence ? ???? ??? ??? ???? ?? ??? ??. (?? ???? ? ??) ? ?? ? P ?? ?? ??? ?? ??? ????, ? Q ?? ?? ???? ???? ???? ?? ? ?? ?? ???? ?? ???? KL-divergence ??? ??ĪŁ ?? ?? ?. ? (????)
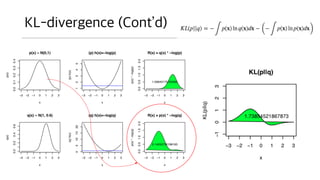
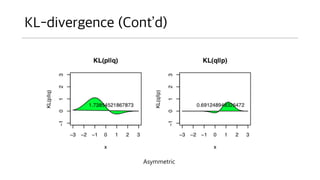
- 21. KL-divergence (ContĪ»d) ? ? ?? ?? ??? ?? ?? ????? ???? ?? 0?? ? ? ??? ? ?? ??? ??? ?? ??? ??? ??? ?? ???? ??? ??? ?? ?? ?? ?? ???. ? ?? ??? ?? ?? ??? ?? ???? ??? ? ??? ????? ?? ??? (?? ??) ??? ? ?? ??.
- 23. KL-divergence (ContĪ»d) ? ?? ??? ??? ? ??? ??? ?? P ? ??? ???? ??? P ??? ??? ?????, ? ?? Q?? ?? ??? ???? ?? ?? P ?? ? ??? ??. ? ?? ?? ???? ?? ???? ???? KL ?? ???? ?? ??? ???. ? ?? ?? Q1, Q2 ? ???? ?? KL? P? ?? ???? Q1? ? ??. ? ??? Q1 ? Q2 ?? P? ? ??? ????? ??? ? ??. ? ??? ?? ????? ? ?? ???. ? ?? ??? ??? ??? ????? ???? ??? ??. ? ??? ??? ? ? ??? ????? ?????. ? P ?? ???? ?? ??? ??? ??? ? ???? KL ?? ????.
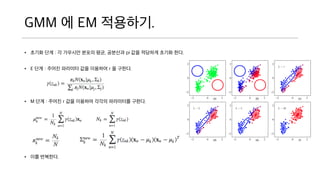
- 24. EM (Expectation- Maximization) ?????? ?? EM ????? ???? ??.
- 25. Mixture Distribution ? ???? ?? ??? ???? ?? ?? ???? ???? ??? ?? ? ????. ? ?? ?? ???? ??(distribution)?? ?? ????. ? ????, ????, ??? ??, ????-t ??, ?? ??, ?? ?? ?? ? ???? ????? ??? ???? ???? ??? ????? ?? ??. ? ??? ???? ?? ?? ??? ??? ???? ?? ??? ????. ? ? ? ?? ??? ??? GMM (Gaussian Mixture Model) ? ????. ? ?? ?? (latent variable)? ???? ??? ??? ???? ??.
- 26. K-means ???? ? EM ? K-means ????? ?? ??? ??. ? ??? ???? K ?? ???? ??????? ????. ? ?? ??? ??? ???? ?? ??? ????? ???? ???? ?. ? ?? ?? K ?? ???(central point)? ????, ? ?? ???? ??? ?? ??? ???? ???? ????. ? ?? ?? ?? ??? ??? ??. ? = ?=1 ? ?=1 ? ??? ? ? ? ? ? 2 ??? = 1, ?? ? = ?????? ? ? ? ? ? ? 2 0, ????????? Binary indicator variables
- 27. K-means ???? ? MLE? ????. ??? = 1, ?? ? = ?????? ? ? ? ? ? ? 2 0, ????????? ? ? ?? ????? ?? ???? ??. ? ???? ??? ??. ? ?? ????? ???? ??? ?? ? ????? ?????? ?? ? GD? ????.
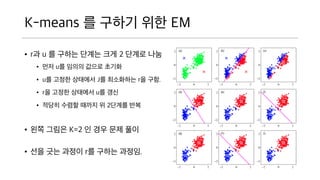
- 28. K-means ? ??? ?? EM ? r? u ? ??? ??? ?? 2 ??? ?? ? ?? u? ??? ??? ??? ? u? ??? ???? J? ????? r? ??. ? r? ??? ???? u? ?? ? ??? ??? ??? ? 2??? ?? ? ?? ??? K=2 ? ?? ?? ?? ? ?? ?? ??? r? ??? ???.
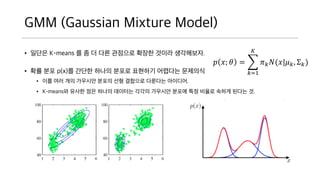
- 29. GMM (Gaussian Mixture Model) ? ??? K-means ? ? ? ?? ???? ??? ??? ?????. ? ?? ?? p(x)? ??? ??? ??? ???? ???? ???? ? ?? ?? ?? ???? ??? ?? ???? ???? ????. ? K-means? ??? ?? ??? ???? ??? ???? ??? ?? ??? ??? ??? ?. ? ?; ? = ?=1 ? ? ? ?(?|? ?, ”▓ ?)
- 30. GMM (Gaussian Mixture Model) (ContĪ»d)
- 31. GMM with latent variable ? ?? ?? z ? ???? GMM ? ????. Responsibility
- 32. MLE for GMM ? ??? ??? ??? ???? ?? ?? ????.
- 33. GMM ? EM ????. ? ??? ?? : ? ???? ??? ??, ???? pi ?? ???? ??? ??. ? E ?? : ??? ???? ?? ???? r ? ???. ? M ?? : ??? r ?? ???? ??? ????? ???. ? ?? ????.
- 34. EM ? ?? ? ?? ???. ? ?? ???? ??? ???? ??? ??. ? ?? ?? ?? z ? ???? ???? ??? ?? ? ??. ? z ? ?? ?? ??? ?? ??. ?? ???? ??? ??? ?? ??. ? ?? ??? EM ? ???? ??. ? SGD ? ?? ?? z ? ???? ?? ?? ??? ????? ?. ? ???? ?? ??? ??? ? ???? ?? ???? ????. ? ??? ??? ? ?? ??? ? ????.
- 35. Expectation of log likelihood. ? ????? ? ??? ??? MLE ??? ??? ? ??. ? ?? ??? ??? ?? ????? ???? MLE? ??. ? ??? ??? ?? ?? ??? ???? Ī░????Ī▒? Ī░ZĪ▒? ???. (?????)
- 37. EM ? ??? ? ?? ???? ? ??? ?????? EM ??? ??. ? ?? ?? ?? z ? ??? ? ?? ????? ??. ? ?? ?? z ?? ??? ?? ??? ???? ???, ? z ? ???? ?? ?? ??? ??? ???? ??? ? ??. ? ?, ?? ??? ??? ? Z ? ???? ?? ??? ? ?? ??? ??? ? ???? ???? ??? ???? ??. (GMM??)
- 38. EM ???? ??. ? ??? EM ????? ?? ??? ??? ????? ??. ? MLE ??? ? ???? ??? ? ???? ?? EM ???? ?? ? ? ??. ? ??? ??? ?? ?? ?? ?? ?? ???!!! ??? ?? ??. ? ?? z ? ???? ??? ? ? ?? ??? ??. ? ??? ??? z ? ? ??? ??. ? ??? ??? z? ???? ??? ?? ???? ??? ?????
- 39. EM ???? ??. (ContĪ»d) ? EM ? ???? Z? ?? ???? MLE? ??? ??. ? p(x) ? ???? ?? ??? ???? ?? ??? ???. (incomplete-data) ? p(x, z) ? MLE? ?? ?? ? ?? ??. (complete-data) ? Z ? ?? ????(?, PMF)? ?? ??? ??. ? ?? ?? ?? (PDF)? ???? ?? ???? ??? ??? ???? ???. ? ?? ?? p(z|x) ? ??? ?? ??? ???. ? ??? ??? ??? ????? ???? ??? ??. (E-Step??) ? ??? ?? ??????? -> VI
- 41. q(z)? ?? ? ?? VI ?? ???? ?? ???? q(z)? ????. ? ??? ?? ?? ???? ?? ??? z ? ??? ?? ?? ?? ?? q() ?. ? ?? z? ??? ?? ?? ?? q(z)? ????? ? ? ?? ?? ??? ?? ?? ? ???.
- 42. Variational Inference log ? ?; ? ? ? Īį ?(?|?)?(?, ?) ??(?||?)
- 43. EM for VI ? L? ?????. (??? q ? ? ??) ? ??? ? ? ???? ?? ??. ? KL ? ?? ?????. ? ? ?? ? ?? ???? ?? ? ??. ? ??? ??? ? ? ??? ?? ? ?.
- 44. ?? ? ??? ???? ??? ?? ????? ????. ? JensenĪ»s Inequality (?? ???) ©C ?? f ? convex ? ?? ??? ??. ? GibbĪ»s Inequality (?? ???) ©C p ? q ? ?? ?? ??? ??? ?.
- 45. ?? (ContĪ»d)
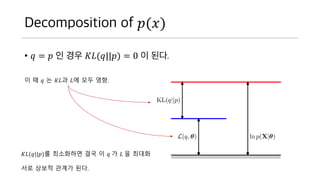
- 46. Decomposition of ?(?) ? ? = ? ? ?? ??(?||?) = 0 ? ??. ? ? ? ? ??? ?? ?? ??. ??(?||?)? ????? ?? ? ? ? ? ? ??? ?? ??? ??? ??.
- 47. E-Step ? ???? ? ? ???? ???? ?? ? ? ??? ? ??(?||?) = 0 ??? ???? ????. ? ??? ? ? ???? Bound ?? ? ? ???.
- 48. M-Step ? ?? ? ? ??? ???? ???? ? ? ??? ? ?? MLE ? ???? ??? ? ? ?? ??. ? ?? ??? ? ? ?? Bound ?? ? ? ???.
- 49. Overview for EM ? ? ??? EM? ?? ?? ???? ????. ? ?? ??? ???? ? ??? ??? EM ????? ??? ? ?? ???? ?? ??? ??? ??? ??? ? ??? ??? ??. ? ? ? ? ??? ? ??? ? ?? concave ????? ?? ?? ??? ??. (?? ?) ? ? ??? E-Step?? ?????. ? ??? ? ??? ????? ??? ???? ?? ???? ??. ? ?? ????? ? ??? ??. ? ?? ???? ??? ? ??? ??. (???) ? ? ??? M-Step ????. ? ?? ??? ??? ??? ???? ??.
- 50. VI (Variational Inference) ?? ?? ?????.
- 51. ??? (Variational Method) ? ???? ???? ?????? ?? ???? ?? ? ?? ??? ??? ???? ??? ???? ???, ? ??? ???? ?? ??? ??? ? ??. : ?? ?? ???(functional). ? ???? ??? ???? ??. ? ???? ???? ??? ?? ?? ? ??? ???? ???? ??. ? ??? ??? ?? ??? ???. ? ??? VI ??? ?? ??? ??? ??? ???? ??? ??? ????? ?. ? ???? ?? ???? ? ????(quadratic) or ?? ??? ??? ?? ?? or ?? ??
- 52. VI ??? ?? ? VI ? ??? ?? ?? ????? ?? ??? ???? ??. ? ?, Full Bayesian ??? ??. ? ??? ??? ?? ????? ?? Z ? ????. ? ??? ???? ?? ???? ?? latent variable ? ????. ? ?? ?? latent variable ? ??? ??(continuous random variable)? ? ???. ? ?? ?? ???? ??? ???? ???? ??? ???? ???? ??. ? ?? ? ?? ?(?) ? ?? ?? ?(?|?) ? ?? ??? ?? ??? ?? ?.
- 53. ???? ???? ??. ? ? ?? ?? ???? ?????? ?? ?? ??? ?????. ? ?? ??? ?? ?? ????? ?? ??? ???? Full ???? ?? ? ?? ? ???? ?? ??? ??? ?? ? ??? ?? ??? ?? ???? ???? ???? ??.
- 54. ???? ???? ??. (ContĪ»d) ? ?? Z ? ?? ???? ??(family) ? ??? ??. ? KL? ????? ?? ???? ?? ?? ? ?? ?? ??? ? ????? ???? ?? ?? : ?(?; ?) ? ?? ?? ??. ? Factorized distributions
- 55. Factorized distributions ? [??] ??? ? ? ??? ??? ? ??? ???? ? ??. ? ?, ??? ? ? ?? ?????? ??? ? ? ??. ? ?? ?? ??? ?(?) ? ????? ? ? ???. ? ??? ??? ??? ?? (mean-field theory) ??? ??.
- 56. ??? ?? ? ??? ??????? ??? ?? ?????? ?? ?? ?? ? ??. ? (self-consistent field theory)??? ?. (? ???) ? ??? ????? ?? ???(many-body) ??? ??? ??? ????(one-body)? ?? ??? ???? ?? ? ??? ??? ?? ????? ???? ???? ????, ?? ?? ??? ? ???? ?









![MLE (Maximum Likelihood Estimation)
? = ? ?; ?
[??]
?? ???? ?? ????? ????.
????? ?? ??? ??
?? ??? likelihood ?? ??? ???.
? ?; ?
? ?? ?; ? ??
?? ?? p(x)??? ??? ??????,
? ??? ???? ??? L ??? ????.
??
? ?; ? = ?????? ? ?(?; ?)](https://image.slidesharecdn.com/vi-170405044222/85/Variational-inference-intro-korean-ver-11-320.jpg)

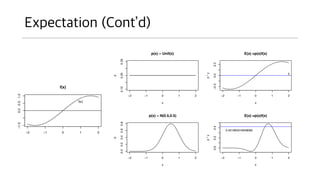
![Expectation
? ?? ?? ?? ???(??)?? ???? ??? ??. (? ?
[?])
? ??? ?? ??? ?? ??? ?? ???.
? ?? ????? ???? ??? ????? ????? ??.
? ?? ??? ???? ?????
? ? [?] = ?? ? ?? , ? ? [?] = ? ? ? ? ??](https://image.slidesharecdn.com/vi-170405044222/85/Variational-inference-intro-korean-ver-13-320.jpg)
































![Factorized distributions
? [??] ??? ? ? ??? ??? ? ??? ???? ? ??.
? ?, ??? ? ? ?? ?????? ??? ? ? ??.
? ?? ?? ??? ?(?) ? ????? ? ? ???.
? ??? ??? ??? ?? (mean-field theory) ??? ??.](https://image.slidesharecdn.com/vi-170405044222/85/Variational-inference-intro-korean-ver-55-320.jpg)

