![Antonio Šabić
11 710 0,700 4,750 4461,058
12 715 0,775 4,500 4492,474
13 720 0,925 4,500 4523,890
14 725 0,800 4,375 4555,306
15 730 0,800 4,375 4586,721
16 735 0,750 4,500 4618,137
17 740 0,700 4,750 4649,553
18 745 0,065 4,750 4680,969
19 750 0,600 4,875 4712,385
Kako bi mogli nacrtati graf, prvo smo morali odredite kutnu frekvenciju za svaku od vrijednosti
frekvencija funkcijskog generatora, po formuli:
f 2 .
Dobivenu rezonantnu frekvenciju moramo usporediti s onom dobivenom iz jednadžbe:
0
1
LC
.
Kako znamo da je induktivitet zavojnice 1 H, a kapacitorska dekada namještena na 50 nF, tada
po formuli ω iznosi:
0 4472,140 s-1
Rezonantna frekvencija koju smo mogli uočiti iz naše tablice i grafa je:
4523,890 s-1
U četvrtom zadatku trebamo odrediti radni otpor zavojnice RL, pomoću jednadžbe:
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 1000 2000 3000 4000 5000
UTO[V]
ω [s-1]
Ovisnost UTO o ω
UTO (V)](https://image.slidesharecdn.com/vjeba5-150101162602-conversion-gate02/85/Vjezba-5-7-320.jpg)
Vježba 5
- 1. Antonio Šabić VJEŽBA 5: ELEKTRIČNI TITRAJNI KRUG UVOD: Serijski spojen otpornik, zavojnicu i kapacitor u krug izmjenične struje nazivamo električnim tirajnim (ili serijskim RLC) krugom (slika ispod). Za strujni krug na gornjoj slici vrijedi Drugi Kirchoffov zakon: 0)( CLR UUUtU , gdje smo s UR, UL i UC označili padove napona na otporniku otpora R, zavojnici koeficijenta samoindukcije L i kapacitoru kapaciteta C. Napon koji se stvara na krajevma otpornika je jednak umnošku struje I, koja prolazi strujnim krugom, i njegovog otpora R: RIUR . Kada kroz zavojnicu prolazi vremenski ovisna struja I, na njenim se krajevima inducira električni napon koji je po Faradayevom zakonu indukcije jednak: dt d NUL , gdje je N broj navoja zavojnice, φ magnetski tok kroz zavojnicu, a negativni predznak govori da je inducirani napon po predznaku suprotan naponu koji izaziva protjecanje električne struje (Lenzovo pravilo). Magnetski tok φ ovisi o struji I koja protječe zavojnicom te se napon UL može prikazati i preko električne struje I: dt dI LUL . L je fizikalna veličina određena samom zavojnicom i naziva se koeficijentom samoindukcije zavojnice. Napon na krajevima kapacitora UC je jednak omjeru napona na njegovm pločama Q i njegovom kapacitetu C: C Q UC .
- 2. Antonio Šabić Vremenski promjenljiva struja I dovodi do vremenske promjene napona na kapacitoru po sljedećem zakonu: dt dQ I . Koristeći izraze za UR, UL i UC, Drugi Kirchoffov zakon se može napisati ovako: 0)( C Idt dt dI LIRtU . Diferenciranjem gornje jednadžbe po vremenu dobijemo diferencijalnu jednadžbu drugoga reda za struju I: dt tdU I Cdt dI R dt Id L )(1 2 2 . Napon i struja su vremenski promjenljive veličine te ih se može zapisati kompleksnim brojevima: ti ti eUtU eItI 0 0 )( )( Fizikalno mjerljive veličine su realni djelovi kompleksne struje i napona. Zapis putem kompleksnih brojeva olakšava matematičko manipuliranje i omogućuje zorniji prikaz faznih odnosa između struje i napona. I0 i U0 su amplitude struje i napona, a ω je frekvencija struje i napona i definira se preko perioda T: T v 2 2 , Kombiniranjem diferencijalne jednadžbe za Drugi Kirchoffov zakon i jednadžbi za napon i struju dobijemo: 0 0 00 2 Ui C I RIiLI , iz koje se dobije odnos između amplitude napona i struje: 00 1 I C LiRU . Izraz unutar uglate zagrade se naziva kompleksnom impedancijom serijskog RLC kruga i označava se slovom Z:
- 3. Antonio Šabić C LiRZ 1 . Kompleksna impedancija Z u krugu izmjenične struje je kompleksni broj. Primjetite da u krugu istosmjerne struje (u kojemu je ω = 0) impedancija postaje jednaka otporu R i realan je broj. Na slici a) je prikazana impedancija Z u kompleksnoj ravnini. Otpor otpornika R (koji se još naziva i radnim otporom) je realan broj jer on ne izaziva fazni pomak napona prema struji. Kapacitivni otpor kapacitora 1/iωC stvara fazni pomak od +π/2 napona prema struji. Nasuprot tome, induktivni otpor iωL koji nastaje na krajevima zavojnice izaziva kašnjenje napona za strujom za kut π/2. Ukupna impedancija Z je vektorski zbroj radnog, kapacitvnog i induktivnog otpora. Na slici b) su u kompleksnoj ravnini prikazani naponi na otporniku UR, zavojnici UL i kapacitoru UC. Iz jednadžbe odnosa između amplitude napona i struje vidimo da između napona i struje postoji fazni pomak definiran impedancijom Z. Uzmimo da je faza struje jednaka nuli te je crtamo na realnoj osi. Napon je izračunat vektroskim zbrajanjem padova napona na radnom, kapacitivnom i induktivnom otporu i prema struji je fazno pomaknut za kut ϕ čiji se tangens računa iz formule: R C L tg 1 . Ponovimo da fizikalni smisao imaju samo realne komponente napona i struje. Značenje faznog pomaka je da napon i struja ne dosižu svoje maksimalne vrijednosti u istom trenutku. Kada je fazni pomak jednak nuli, odnosno kada je ispunjen uvjet: LC 1 0 , kažemo da je RLC krug u rezonanciji, a frekvencija ω0 se naziva rezonantnom frekvencijom. Na slici ispod je prikazana kompleksna impedancija za slučajeve ω < ω0, ω = ω0 i ω > ω0. Za male frekvencije je 1/ωC puno veći od ωL, te impedancija Z ima fazu približno jednaku +π/2 (odnosno, napon prema struji „brza“ za π/2). U slučaju visokih frekvencija, ωL postaje puno veći od 1/ωC zbog čega impedancija Z ima fazu –π/2 (drugim riječima, napon za strujom „kasni“ za π/2). U rezonanciji (ω = ω0) kapacitivni i indukivni otpor se poništavaju i impedancija postaje realni broj.
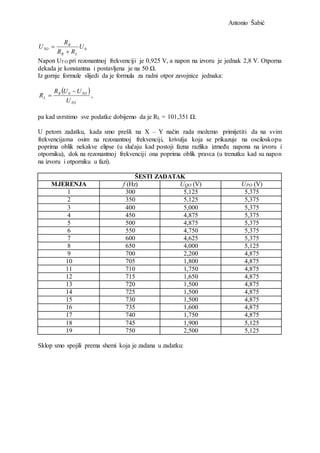
- 4. Antonio Šabić Zamislimo da imamo naponski izvor, odnosno izvor koji daje stalnu vrijednost amplitude napona. Na temelju jednadžbe odnosa između amplitude napona i struje možemo odrediti odnos između apsolutnih vrijednosti napona i struje: 2 2 0 0 1 C LR U I . Pribor koji nam je potreban je osciloskop, funkcijski generator, otporna dekada koju je potrebno namjestiti na otpor od 50 Ω, kapacitorska dekada koju namjestimo na kapacitet od 50 nF i zavojnicu induktiviteta 1 H. U prvom zadatku priključimo osciloskop na funkcijski generator. Na temelju perioda po jednog sinusoidalnog, pilastog i pravokutnog signala odredite njegovu kružnu frekvenciju ω. Trebamo je usporediti s frekvencijom ν prikazanom na funkcijskom generatoru (ω = 2πν). U drugom zadatku trebamo spojiti sklop prema shemi prikazanoj na slici. Na jedan od ulaznih kanala osciloskopa trebamo spojiti napon UPO (napon izvora amplitude U0), a na drugi napon UTO (napon na krajevima otpornika). Funkcijski generator trebamo postavite da daje sinusoidalni napon, te mu frekvenciju ν mijenjati od 200 Hz do 1 kHz i trebamo bilježiti napon UTO za različite frekvencije, te uočiti pojavu rezonancije. U okolini rezonancije obaviti najgušća mjerenja i zabiježiti napon UPO. Što se događa s međusobnom fazom napona UPO i UTO? U trećem zadatku trebamo nacrtati graf UTO = f(ω) i iz njega odrediti rezonantnu frevenciju ω0, te je usporediti s rezonantnom frekvencijom iz jednadžbe: LC 1 0 . U četvrtom zadatku trebamo odrediti radni otpor zavojnice RL pomoću jednadžbe: 0U RR R U LR R TO U petom zadatku trebamo prijeći na X –Y način rada i pratiti oblik krivulje na ekranu za različite frekvencije ν, te prokomentirati rezultat. U šestom zadatku trebamo spojiti sklop kao na slici. Na jedan od ulaznih kanala osciloskopa spojiti napon UPO (napon izvora amplitude U0), a na drugi napon UQO (napon na krajevima serijskog spoja zavojnice i kapacitora). Funkcijski generator trebamo postaviti da daje
- 5. Antonio Šabić sinusoidalni napon, frekvenciju ν mu mijenjati od 200 Hz do 1 kHz i bilježiti napon UQO za različite frekvencije, te uočiti pojavu rezonancije. U okolini rezonancije trebamo obaviti najgušća mjerenja, te zabiježiti napon UPO. MJERENJA: PRVI ZADATAK VRSTA SIGNALA T (ms) ω (rad/s) f (Hz) ν (Hz) SINUSOIDALNI 2,50 2513,27 400,00 400,70 PILASTI 2,30 2731,82 434,78 438,40 PRAVOKUTNI 2,10 2991,99 476,19 470,50 Pri izvođenju prvog zadatka na osciloskopu smo očitali vrijednosti perioda, te smo kružnu frekvenciju izračunali prema formuli: T 2 . Frekvenciju f, koja bi trebala biti približno jednaka frekvenciji ν funkcijskog generatora smo izračunali po formuli: T f 1 . DRUGI ZADATAK MJERENJA f (Hz) UTO (V) UPO (V) 1 300 0,030 5,125 2 350 0,036 5,125 3 400 0,047 5,125 4 450 0,057 5,125 5 500 0,075 5,125 6 550 0,105 5,125 7 600 0,180 5,125 8 650 0,275 5,125 9 700 0,600 4,750 10 705 0,650 4,750 11 710 0,700 4,750 12 715 0,775 4,500 13 720 0,925 4,500 14 725 0,800 4,375 15 730 0,800 4,375 16 735 0,750 4,500 17 740 0,700 4,750 18 745 0,065 4,750 19 750 0,600 4,875 Mjerenje otpora na otporniku se obavljamo po sljedećoj shemi (slika ispod):
- 6. Antonio Šabić Realna zavojnica uvijek ima i radni otpor koji je na slici označen s RL. Otpor otpornika smo označili s RR te je ukupni radni otpor R u strujnom krugu na slici jednak zbroju otpora zavojnice i otpornika: LR RRR . Amplituda napona između točaka T i O (odnosno, na krajevima otpornika) je jednaka umnošku amplitude struje koja protječe otpornikom i njegovog radnog otpora: 2 2 0 0 1 LR R RTO RR C L UR RIU . Napon UTO u rezonanciji poprima maksimalnu vrijednost i jednak je: 0U RR R U LR R TO . Dakle, u ovom zadatku smo za različite vrijednosti frekvencija na funkcijskom generatoru bilježili napone UPO i UTO. Dok smo mjerili mogli smo uočiti da su grafovi napona UPO i UTO u fazi na otprilike 720 Hz. Ako strujni krug nije u rezonanciji, postoji razlika u fazi između napona na izvoru i otporniku. TREĆI ZADATAK MJERENJA f (Hz) UTO (V) UPO (V) ω (s-1) 1 300 0,030 5,125 1884,954 2 350 0,036 5,125 2199,113 3 400 0,047 5,125 2513,272 4 450 0,057 5,125 2827,431 5 500 0,075 5,125 3141,590 6 550 0,105 5,125 3455,749 7 600 0,180 5,125 3769,908 8 650 0,275 5,125 4084,067 9 700 0,600 4,750 4398,226 10 705 0,650 4,750 4429,642
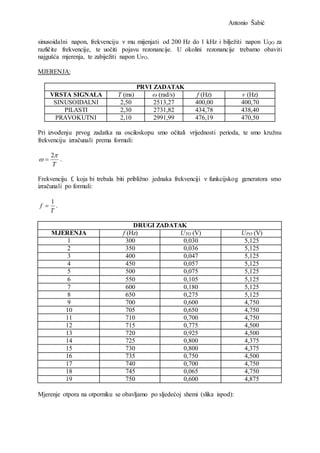
- 7. Antonio Šabić 11 710 0,700 4,750 4461,058 12 715 0,775 4,500 4492,474 13 720 0,925 4,500 4523,890 14 725 0,800 4,375 4555,306 15 730 0,800 4,375 4586,721 16 735 0,750 4,500 4618,137 17 740 0,700 4,750 4649,553 18 745 0,065 4,750 4680,969 19 750 0,600 4,875 4712,385 Kako bi mogli nacrtati graf, prvo smo morali odredite kutnu frekvenciju za svaku od vrijednosti frekvencija funkcijskog generatora, po formuli: f 2 . Dobivenu rezonantnu frekvenciju moramo usporediti s onom dobivenom iz jednadžbe: 0 1 LC . Kako znamo da je induktivitet zavojnice 1 H, a kapacitorska dekada namještena na 50 nF, tada po formuli ω iznosi: 0 4472,140 s-1 Rezonantna frekvencija koju smo mogli uočiti iz naše tablice i grafa je: 4523,890 s-1 U četvrtom zadatku trebamo odrediti radni otpor zavojnice RL, pomoću jednadžbe: 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 1000 2000 3000 4000 5000 UTO[V] ω [s-1] Ovisnost UTO o ω UTO (V)
- 8. Antonio Šabić 0U RR R U LR R TO Napon UTO pri rezonantnoj frekvenciji je 0,925 V, a napon na izvoru je jednak 2,8 V. Otporna dekada je konstantna i postavljena je na 50 Ω. Iz gornje formule slijedi da je formula za radni otpor zavojnice jednaka: TO TOR L U UUR R 0 , pa kad uvrstimo sve podatke dobijemo da je RL = 101,351 Ω. U petom zadatku, kada smo prešli na X – Y način rada možemo primijetiti da na svim frekvencijama osim na rezonantnoj frekvenciji, krivulja koja se prikazuje na osciloskopu poprima oblik nekakve elipse (u slučaju kad postoji fazna razlika između napona na izvoru i otporniku), dok na rezonantnoj frekvenciji ona poprima oblik pravca (u trenutku kad su napon na izvoru i otporniku u fazi). ŠESTI ZADATAK MJERENJA f (Hz) UQO (V) UPO (V) 1 300 5,125 5,375 2 350 5,125 5,375 3 400 5,000 5,375 4 450 4,875 5,375 5 500 4,875 5,375 6 550 4,750 5,375 7 600 4,625 5,375 8 650 4,000 5,125 9 700 2,200 4,875 10 705 1,800 4,875 11 710 1,750 4,875 12 715 1,650 4,875 13 720 1,500 4,875 14 725 1,500 4,875 15 730 1,500 4,875 16 735 1,600 4,875 17 740 1,750 4,875 18 745 1,900 5,125 19 750 2,500 5,125 Sklop smo spojili prema shemi koja je zadana u zadatku:
- 9. Antonio Šabić Pomoću sklopa prikazanog na slici možemo osciloskopom pratiti napon na kapacitoru i zavojnici. Napon između točaka Q i O je napon na krajevima serijskog spoja zavojnice i kapacitora: 2 2 2 2 0 2 2 0 1 1 1 LR L LQO RR C L C LR U C LRIU . U rezonanciji je napon UQO jednak: 0U RR R U LR L QO . Prema mjerenjima u tablici vidimo da se rezonancija događa pri frekvencijama od 720 Hz do 730 Hz. Kada smo prešli u X – Y način rada mogli smo preciznije odrediti da je rezonantna frekvencija negdje oko 726 Hz. KOMENTAR: Kod prvog zadatka dolazi do malog odstupanja između rezonantne frekvencije funkcijskog generatora i one koje smo mi mjerili (jedine greške su mogle nastati zbog nepreciznog očitavanja vrijednosti na osciloskopu). Odstupanja pri mjerenju su se dogodila najvjerojatnije zbog nesavršenosti mjernog aparata (prikaz funkcija na osciloskopu i već prije spomenuti problem), te povremenog titranja slike na zaslonu osciloskopa koje je moglo utjecati na očitavanje vrijednosti, zbog toga što jedna od žica nije bila u redu pa je trebalo tražiti optimalan kontakt.