Irisan 2
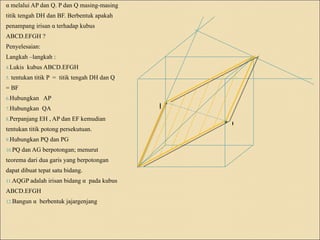
- 1. α melalui AP dan Q. P dan Q masing-masing titik tengah DH dan BF. Berbentuk apakah penampang irisan α terhadap kubus ABCD.EFGH ? Penyelesaian: H G Langkah –langkah : 4.Lukis kubus ABCD.EFGH 5. tentukan titik P = titik tengah DH dan Q E F = BF 6.Hubungkan AP 7.Hubungkan QA P 8.Perpanjang EH , AP dan EF kemudian Q tentukan titik potong persekutuan. 9.Hubungkan PQ dan PG 10.PQ dan AG berpotongan; menurut C D teorema dari dua garis yang berpotongan dapat dibuat tepat satu bidang. A B 11.AQGP adalah irisan bidang α pada kubus ABCD.EFGH 12.Bangun α berbentuk jajargenjang