Tech Lab Paak講演会 20150601
- 3. 目次はこのような内容 第1章 データマイニングとは 第2章 Rを使ってみよう 第3章 その2つのデータ,本当に差があるの? ~仮説検定~ 第4章 ビールの生産計画を立てよう~重回帰分析~ 第5章 自社サービス登録会員をグループ分けしてみよう ~クラスタリング~ 第6章 コンバージョン率を引き上げる要因はどこに? ~ロジスティック回帰~ 第7章 どのキャンペーンページが効果的だったのか? ~決定木~ 第8章 新規ユーザーの属性データから今後のアクティブユーザー数を 予測しよう ~SVM/ランダムフォレスト~ 第9章 ECサイトの購入カテゴリデータから何が見える? ~アソシエーション分析~ 第10章 Rでさらに広がるデータマイニングの世界 ~その他の分析メソッドについて~ 3
- 4. 要約するとこのような内容 第1章 データマイニング概観 第2章 R入門 第3章 仮説検定 第4章 重回帰分析(正規線形モデル) 第5章 クラスタリング(Ward法、K-means、EM) 第6章 ロジスティック回帰 第7章 決定木 第8章 SVM/ランダムフォレスト 第9章 アソシエーション分析 第10章 GLM、生存分析、グラフ理論、MCMCなど 4
- 6. 6 …?
- 12. プロテニス四大大会のデータ Result Result of the match (0/1) - Referenced on Player 1 is Result = 1 if Player 1 wins (FNL.1>FNL.2) FSP.1 First Serve Percentage for player 1 (Real Number) FSW.1 First Serve Won by player 1 (Real Number) SSP.1 Second Serve Percentage for player 1 (Real Number) SSW.1 Second Serve Won by player 1 (Real Number) ACE.1 Aces won by player 1 (Numeric-Integer) DBF.1 Double Faults committed by player 1 (Numeric-Integer) WNR.1 Winners earned by player 1 (Numeric) UFE.1 Unforced Errors committed by player 1 (Numeric) BPC.1 Break Points Created by player 1 (Numeric) BPW.1 Break Points Won by player 1 (Numeric) NPA.1 Net Points Attempted by player 1 (Numeric) NPW.1 Net Points Won by player 1 (Numeric) FSP.2 First Serve Percentage for player 2 (Real Number) FSW.2 First Serve Won by player 2 (Real Number) SSP.2 Second Serve Percentage for player 2 (Real Number) SSW.2 Second Serve Won by player 2 (Real Number) ACE.2 Aces won by player 2 (Numeric-Integer) DBF.2 Double Faults committed by player 2 (Numeric-Integer) WNR.2 Winners earned by player 2 (Numeric) UFE.2 Unforced Errors committed by player 2 (Numeric) BPC.2 Break Points Created by player 2 (Numeric) BPW.2 Break Points Won by player 2 (Numeric) NPA.2 Net Points Attempted by player 2 (Numeric) NPW.2 Net Points Won by player 2 (Numeric) 12 Caroline Wozniacki (from Wikimedia Commons)
- 13. プロテニス四大大会のデータ(和訳) Result プレイヤー1が勝てば1、2が勝てば0 (以下プレイヤー1/2共通) FSP.1/2 ファーストサーブ確率 FSW.1/2 ファーストサーブポイント獲得率 SSP.1/2 セカンドサーブ確率 SSW.1/2 セカンドサーブポイント獲得率 ACE.1/2 サービスエース数 DBF.1/2 ダブルフォールト数 WNR.1/2 ストロークウィナー数 UFE.1/2 アンフォーストエラー数 BPC.1/2 ブレーク機会創出数 BPW.1/2 ブレークポイント獲得数 NPA.1/2 ネットアプローチ数 NPW.1/2 ネットポイント獲得数 13 Rafael Nadal (from Wikimedia Commons)
- 14. プロテニス四大大会のデータ(男子)の一部 14 Player1 Player2 Result FSP.1 FSW.1 SSP.1 SSW.1 ACE.1 DBF.1 Lukas Lacko Novak Djokovic 0 61 35 39 18 5 1 Leo0rdo Mayer Albert Montanes 1 61 31 39 13 13 1 Marcos Baghdatis Denis Istomin 0 52 53 48 20 8 4 Dmitry Tursunov Michael Russell 1 53 39 47 24 8 6 Juan Mo0co Ernests Gulbis 0 76 63 24 12 0 4 Santiago Giraldo Sam Querrey 0 65 51 35 22 9 3 Dudi Sela Jarkko Nieminen 0 68 73 32 24 5 3 Fabio Fognini Alex Bogomolov Jr. 1 47 18 53 15 3 4
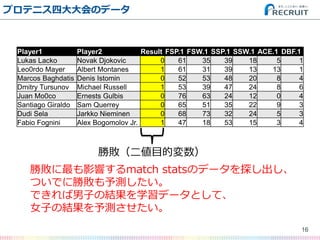
- 15. プロテニス四大大会のデータ 15 Player1 Player2 Result FSP.1 FSW.1 SSP.1 SSW.1 ACE.1 DBF.1 Lukas Lacko Novak Djokovic 0 61 35 39 18 5 1 Leo0rdo Mayer Albert Montanes 1 61 31 39 13 13 1 Marcos Baghdatis Denis Istomin 0 52 53 48 20 8 4 Dmitry Tursunov Michael Russell 1 53 39 47 24 8 6 Juan Mo0co Ernests Gulbis 0 76 63 24 12 0 4 Santiago Giraldo Sam Querrey 0 65 51 35 22 9 3 Dudi Sela Jarkko Nieminen 0 68 73 32 24 5 3 Fabio Fognini Alex Bogomolov Jr. 1 47 18 53 15 3 4 勝敗(二値目的変数) 勝敗に最も影響するmatch statsのデータを探し出し、 ついでに勝敗も予測したい。
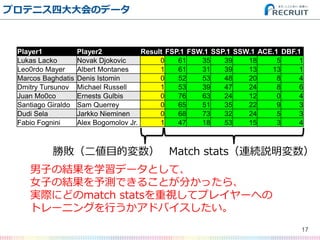
- 16. プロテニス四大大会のデータ 16 Player1 Player2 Result FSP.1 FSW.1 SSP.1 SSW.1 ACE.1 DBF.1 Lukas Lacko Novak Djokovic 0 61 35 39 18 5 1 Leo0rdo Mayer Albert Montanes 1 61 31 39 13 13 1 Marcos Baghdatis Denis Istomin 0 52 53 48 20 8 4 Dmitry Tursunov Michael Russell 1 53 39 47 24 8 6 Juan Mo0co Ernests Gulbis 0 76 63 24 12 0 4 Santiago Giraldo Sam Querrey 0 65 51 35 22 9 3 Dudi Sela Jarkko Nieminen 0 68 73 32 24 5 3 Fabio Fognini Alex Bogomolov Jr. 1 47 18 53 15 3 4 勝敗(二値目的変数) 勝敗に最も影響するmatch statsのデータを探し出し、 ついでに勝敗も予測したい。 できれば男子の結果を学習データとして、 女子の結果を予測させたい。
- 17. プロテニス四大大会のデータ 17 Player1 Player2 Result FSP.1 FSW.1 SSP.1 SSW.1 ACE.1 DBF.1 Lukas Lacko Novak Djokovic 0 61 35 39 18 5 1 Leo0rdo Mayer Albert Montanes 1 61 31 39 13 13 1 Marcos Baghdatis Denis Istomin 0 52 53 48 20 8 4 Dmitry Tursunov Michael Russell 1 53 39 47 24 8 6 Juan Mo0co Ernests Gulbis 0 76 63 24 12 0 4 Santiago Giraldo Sam Querrey 0 65 51 35 22 9 3 Dudi Sela Jarkko Nieminen 0 68 73 32 24 5 3 Fabio Fognini Alex Bogomolov Jr. 1 47 18 53 15 3 4 勝敗(二値目的変数) 男子の結果を学習データとして、 女子の結果を予測できることが分かったら、 実際にどのmatch statsを重視してプレイヤーへの トレーニングを行うかアドバイスしたい。 Match stats(連続説明変数)
- 20. 20 ……
- 22. 例えば ? 「サービスエースが多い方が勝つ」 ? 「ストロークウィナーが多い方が勝つ」 ? 「アンフォーストエラーが少ない方が勝つ」 ? 「ネットポイントが多い方が勝つ」 …などなど 22
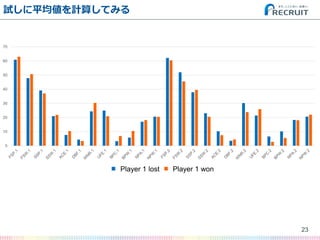
- 23. 試しに平均値を計算してみる 23 0 10 20 30 40 50 60 70 Player 1 lost Player 2 wonPlayer 1 lost Player 1 won
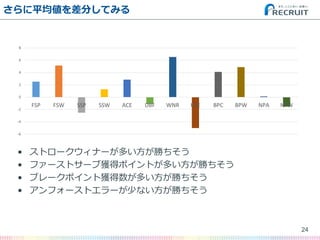
- 24. さらに平均値を差分してみる ? ストロークウィナーが多い方が勝ちそう ? ファーストサーブ獲得ポイントが多い方が勝ちそう ? ブレークポイント獲得数が多い方が勝ちそう ? アンフォーストエラーが少ない方が勝ちそう 24 -6 -4 -2 0 2 4 6 8 FSP FSW SSP SSW ACE DBF WNR UFE BPC BPW NPA NPW
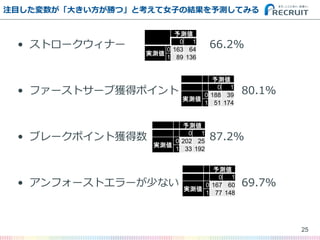
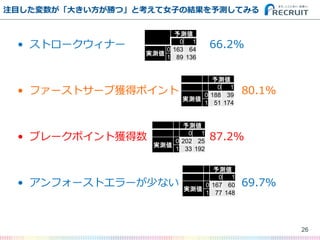
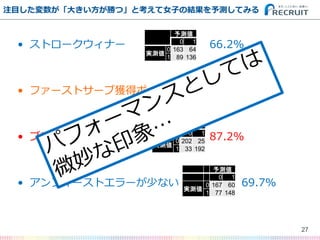
- 25. ? ストロークウィナー 66.2% ? ファーストサーブ獲得ポイント 80.1% ? ブレークポイント獲得数 87.2% ? アンフォーストエラーが少ない 69.7% 注目した変数が「大きい方が勝つ」と考えて女子の結果を予測してみる 25 予測値 0 1 実測値 0 163 64 1 89 136 予測値 0 1 実測値 0 188 39 1 51 174 予測値 0 1 実測値 0 202 25 1 33 192 予測値 0 1 実測値 0 167 60 1 77 148
- 26. ? ストロークウィナー 66.2% ? ファーストサーブ獲得ポイント 80.1% ? ブレークポイント獲得数 87.2% ? アンフォーストエラーが少ない 69.7% 注目した変数が「大きい方が勝つ」と考えて女子の結果を予測してみる 26 予測値 0 1 実測値 0 163 64 1 89 136 予測値 0 1 実測値 0 188 39 1 51 174 予測値 0 1 実測値 0 202 25 1 33 192 予測値 0 1 実測値 0 167 60 1 77 148
- 27. ? ストロークウィナー 66.2% ? ファーストサーブ獲得ポイント 80.1% ? ブレークポイント獲得数 87.2% ? アンフォーストエラーが少ない 69.7% 注目した変数が「大きい方が勝つ」と考えて女子の結果を予測してみる 27 予測値 0 1 実測値 0 163 64 1 89 136 予測値 0 1 実測値 0 188 39 1 51 174 予測値 0 1 実測値 0 202 25 1 33 192 予測値 0 1 実測値 0 167 60 1 77 148
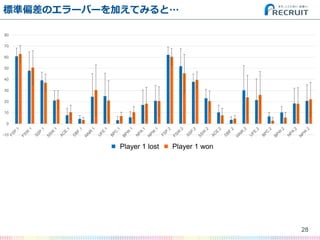
- 28. 標準偏差のエラーバーを加えてみると… 28 -10 0 10 20 30 40 50 60 70 80 Player 1 lost Player 2 wonPlayer 1 lost Player 1 won
- 29. 標準偏差のエラーバーを加えてみると… 29 -10 0 10 20 30 40 50 60 70 80 Player 1 lost Player 2 won 結構ばらつきが大きい… もしかしたら比べても意味がない変数も多い? Player 1 lost Player 1 won
- 31. この辺を統計的検定にかけてみる ? ストロークウィナーが多い方が勝ちそう ? ファーストサーブ獲得ポイントが多い方が勝ちそう ? ブレークポイント獲得数が多い方が勝ちそう ? アンフォーストエラーが少ない方が勝ちそう 31 -6 -4 -2 0 2 4 6 8 FSP FSW SSP SSW ACE DBF WNR UFE BPC BPW NPA NPW
- 32. この辺を統計的検定にかけてみる ? ストロークウィナーが多い方が勝ちそう ? ファーストサーブ獲得ポイントが多い方が勝ちそう ? ブレークポイント獲得数が多い方が勝ちそう ? アンフォーストエラーが少ない方が勝ちそう ?平均値の差の検定=t検定でいける 32 -6 -4 -2 0 2 4 6 8 FSP FSW SSP SSW ACE DBF WNR UFE BPC BPW NPA NPW
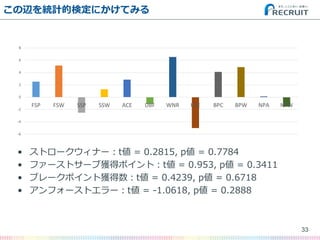
- 33. この辺を統計的検定にかけてみる ? ストロークウィナー:t値 = 0.2815, p値 = 0.7784 ? ファーストサーブ獲得ポイント:t値 = 0.953, p値 = 0.3411 ? ブレークポイント獲得数:t値 = 0.4239, p値 = 0.6718 ? アンフォーストエラー:t値 = -1.0618, p値 = 0.2888 33 -6 -4 -2 0 2 4 6 8 FSP FSW SSP SSW ACE DBF WNR UFE BPC BPW NPA NPW
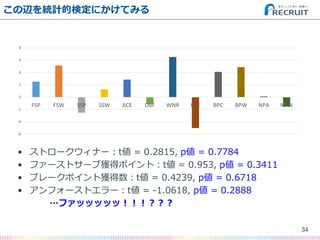
- 34. この辺を統計的検定にかけてみる ? ストロークウィナー:t値 = 0.2815, p値 = 0.7784 ? ファーストサーブ獲得ポイント:t値 = 0.953, p値 = 0.3411 ? ブレークポイント獲得数:t値 = 0.4239, p値 = 0.6718 ? アンフォーストエラー:t値 = -1.0618, p値 = 0.2888 …ファッッッッッ!!!??? 34 -6 -4 -2 0 2 4 6 8 FSP FSW SSP SSW ACE DBF WNR UFE BPC BPW NPA NPW
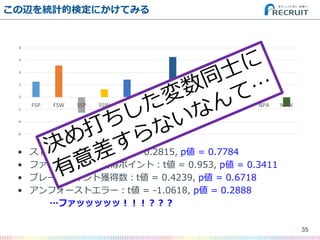
- 35. この辺を統計的検定にかけてみる ? ストロークウィナー:t値 = 0.2815, p値 = 0.7784 ? ファーストサーブ獲得ポイント:t値 = 0.953, p値 = 0.3411 ? ブレークポイント獲得数:t値 = 0.4239, p値 = 0.6718 ? アンフォーストエラー:t値 = -1.0618, p値 = 0.2888 …ファッッッッッ!!!??? 35 -6 -4 -2 0 2 4 6 8 FSP FSW SSP SSW ACE DBF WNR UFE BPC BPW NPA NPW
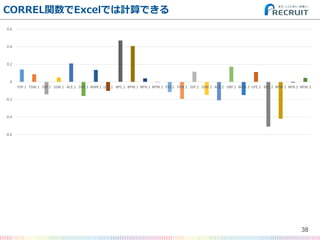
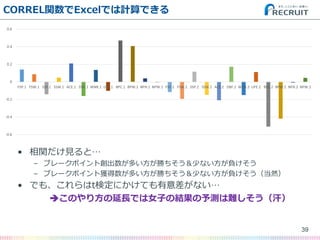
- 38. CORREL関数でExcelでは計算できる 38 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 FSP.1 FSW.1 SSP.1 SSW.1 ACE.1 DBF.1 WNR.1 UFE.1 BPC.1 BPW.1 NPA.1 NPW.1 FSP.2 FSW.2 SSP.2 SSW.2 ACE.2 DBF.2 WNR.2 UFE.2 BPC.2 BPW.2 NPA.2 NPW.2
- 39. CORREL関数でExcelでは計算できる 39 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 FSP.1 FSW.1 SSP.1 SSW.1 ACE.1 DBF.1 WNR.1 UFE.1 BPC.1 BPW.1 NPA.1 NPW.1 FSP.2 FSW.2 SSP.2 SSW.2 ACE.2 DBF.2 WNR.2 UFE.2 BPC.2 BPW.2 NPA.2 NPW.2 ? 相関だけ見ると… – ブレークポイント創出数が多い方が勝ちそう&少ない方が負けそう – ブレークポイント獲得数が多い方が勝ちそう&少ない方が負けそう(当然) ? でも、これらはt検定にかけても有意差がない… ?このやり方の延長では女子の結果の予測は難しそう(汗)
- 46. まずデータを読み込む 46 > dm_raw<-read.table("men.txt",header=T,sep='?t') > dw_raw<-read.table("women.txt",header=T,sep='?t') > dm<-dm_raw[,-c(1,2,14,17,18,19,20,21,27,35,36,37,38,39)] > dw<-dw_raw[,-c(1,2,14,17,18,19,20,21,27,35,36,37,38,39)] https://github.com/ozt-ca/tjo.hatenablog.samples/tree/master/r_samples/public_lib/jp/exp_uci_datasets/tennis
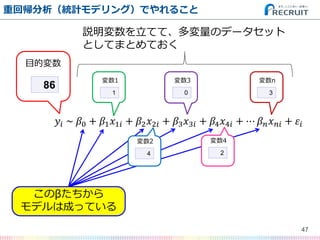
- 47. 47 重回帰分析(統計モデリング)でやれること ?? ~ ?0 + ?1 ?1? + ?2 ?2? + ?3 ?3? + ?4 ?4? + ? ? ? ? ?? + ?? 86 目的変数 1 変数1 4 変数2 0 変数3 2 変数4 3 変数n このβたちから モデルは成っている 説明変数を立てて、多変量のデータセット としてまとめておく
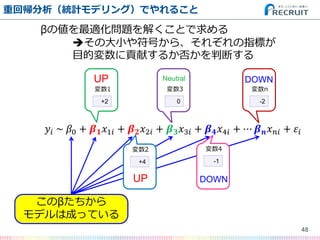
- 48. 48 重回帰分析(統計モデリング)でやれること ?? ~ ?0 + ? ? ?1? + ? ? ?2? + ? ? ?3? + ? ? ?4? + ? ? ? ? ?? + ?? +2 変数1 +4 変数2 0 変数3 -1 変数4 -2 変数n このβたちから モデルは成っている βの値を最適化問題を解くことで求める ?その大小や符号から、それぞれの指標が 目的変数に貢献するか否かを判断する UP UP Neutral DOWN DOWN
- 49. ひとまず神妙にlm関数で… 49 > dm.lm<-lm(Result~.,dm) # lm関数は重回帰分析(正規線形モデル) # つまりLinear Modelを推定するRの関数 > summary(dm.lm) Call: lm(formula = Result ~ ., data = dm) Residuals: Min 1Q Median 3Q Max -0.83231 -0.16572 -0.00958 0.15599 0.91011 # 以下続く
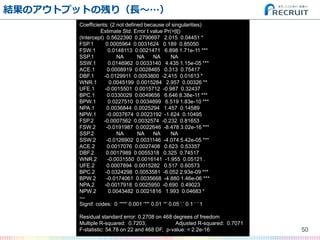
- 50. 結果のアウトプットの残り(長~…) 50 Coefficients: (2 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 0.5622390 0.2790697 2.015 0.04451 * FSP.1 0.0005964 0.0031624 0.189 0.85050 FSW.1 0.0148113 0.0021471 6.898 1.71e-11 *** SSP.1 NA NA NA NA SSW.1 0.0146962 0.0033140 4.435 1.15e-05 *** ACE.1 0.0008919 0.0028465 0.313 0.75417 DBF.1 -0.0129911 0.0053800 -2.415 0.01613 * WNR.1 0.0045199 0.0015284 2.957 0.00326 ** UFE.1 -0.0015501 0.0015712 -0.987 0.32437 BPC.1 0.0330029 0.0049656 6.646 8.38e-11 *** BPW.1 0.0227510 0.0034899 6.519 1.83e-10 *** NPA.1 0.0036844 0.0025294 1.457 0.14589 NPW.1 -0.0037674 0.0023192 -1.624 0.10495 FSP.2 -0.0007562 0.0032574 -0.232 0.81653 FSW.2 -0.0191987 0.0022646 -8.478 3.02e-16 *** SSP.2 NA NA NA NA SSW.2 -0.0126902 0.0031146 -4.074 5.42e-05 *** ACE.2 0.0017076 0.0027408 0.623 0.53357 DBF.2 0.0017989 0.0055318 0.325 0.74517 WNR.2 -0.0031550 0.0016141 -1.955 0.05121 . UFE.2 0.0007894 0.0015282 0.517 0.60573 BPC.2 -0.0324298 0.0053581 -6.052 2.93e-09 *** BPW.2 -0.0174061 0.0035668 -4.880 1.46e-06 *** NPA.2 -0.0017918 0.0025950 -0.690 0.49023 NPW.2 0.0043482 0.0021816 1.993 0.04683 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.2708 on 468 degrees of freedom Multiple R-squared: 0.7203, Adjusted R-squared: 0.7071 F-statistic: 54.78 on 22 and 468 DF, p-value: < 2.2e-16
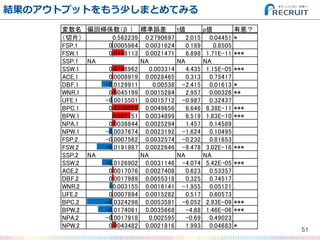
- 51. 結果のアウトプットをもう少しまとめてみる 51 変数名 偏回帰係数(β ) 標準誤差 t値 p値 有意? (切片) 0.562239 0.2790697 2.015 0.04451 * FSP.1 0.0005964 0.0031624 0.189 0.8505 FSW.1 0.0148113 0.0021471 6.898 1.71E-11 *** SSP.1 NA NA NA NA SSW.1 0.0146962 0.003314 4.435 1.15E-05 *** ACE.1 0.0008919 0.0028465 0.313 0.75417 DBF.1 -0.0129911 0.00538 -2.415 0.01613 * WNR.1 0.0045199 0.0015284 2.957 0.00326 ** UFE.1 -0.0015501 0.0015712 -0.987 0.32437 BPC.1 0.0330029 0.0049656 6.646 8.38E-11 *** BPW.1 0.022751 0.0034899 6.519 1.83E-10 *** NPA.1 0.0036844 0.0025294 1.457 0.14589 NPW.1 -0.0037674 0.0023192 -1.624 0.10495 FSP.2 -0.0007562 0.0032574 -0.232 0.81653 FSW.2 -0.0191987 0.0022646 -8.478 3.02E-16 *** SSP.2 NA NA NA NA SSW.2 -0.0126902 0.0031146 -4.074 5.42E-05 *** ACE.2 0.0017076 0.0027408 0.623 0.53357 DBF.2 0.0017989 0.0055318 0.325 0.74517 WNR.2 -0.003155 0.0016141 -1.955 0.05121 . UFE.2 0.0007894 0.0015282 0.517 0.60573 BPC.2 -0.0324298 0.0053581 -6.052 2.93E-09 *** BPW.2 -0.0174061 0.0035668 -4.88 1.46E-06 *** NPA.2 -0.0017918 0.002595 -0.69 0.49023 NPW.2 0.0043482 0.0021816 1.993 0.04683 *
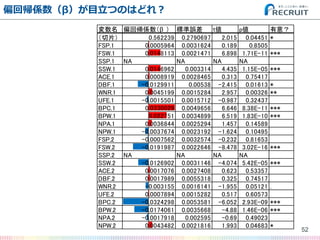
- 52. 偏回帰係数(β)が目立つのはどれ? 52 変数名 偏回帰係数(β ) 標準誤差 t値 p値 有意? (切片) 0.562239 0.2790697 2.015 0.04451 * FSP.1 0.0005964 0.0031624 0.189 0.8505 FSW.1 0.0148113 0.0021471 6.898 1.71E-11 *** SSP.1 NA NA NA NA SSW.1 0.0146962 0.003314 4.435 1.15E-05 *** ACE.1 0.0008919 0.0028465 0.313 0.75417 DBF.1 -0.0129911 0.00538 -2.415 0.01613 * WNR.1 0.0045199 0.0015284 2.957 0.00326 ** UFE.1 -0.0015501 0.0015712 -0.987 0.32437 BPC.1 0.0330029 0.0049656 6.646 8.38E-11 *** BPW.1 0.022751 0.0034899 6.519 1.83E-10 *** NPA.1 0.0036844 0.0025294 1.457 0.14589 NPW.1 -0.0037674 0.0023192 -1.624 0.10495 FSP.2 -0.0007562 0.0032574 -0.232 0.81653 FSW.2 -0.0191987 0.0022646 -8.478 3.02E-16 *** SSP.2 NA NA NA NA SSW.2 -0.0126902 0.0031146 -4.074 5.42E-05 *** ACE.2 0.0017076 0.0027408 0.623 0.53357 DBF.2 0.0017989 0.0055318 0.325 0.74517 WNR.2 -0.003155 0.0016141 -1.955 0.05121 . UFE.2 0.0007894 0.0015282 0.517 0.60573 BPC.2 -0.0324298 0.0053581 -6.052 2.93E-09 *** BPW.2 -0.0174061 0.0035668 -4.88 1.46E-06 *** NPA.2 -0.0017918 0.002595 -0.69 0.49023 NPW.2 0.0043482 0.0021816 1.993 0.04683 *
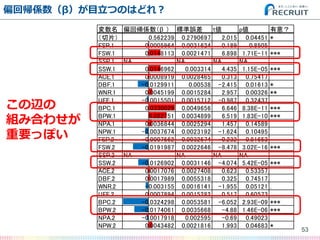
- 53. 偏回帰係数(β)が目立つのはどれ? 53 変数名 偏回帰係数(β ) 標準誤差 t値 p値 有意? (切片) 0.562239 0.2790697 2.015 0.04451 * FSP.1 0.0005964 0.0031624 0.189 0.8505 FSW.1 0.0148113 0.0021471 6.898 1.71E-11 *** SSP.1 NA NA NA NA SSW.1 0.0146962 0.003314 4.435 1.15E-05 *** ACE.1 0.0008919 0.0028465 0.313 0.75417 DBF.1 -0.0129911 0.00538 -2.415 0.01613 * WNR.1 0.0045199 0.0015284 2.957 0.00326 ** UFE.1 -0.0015501 0.0015712 -0.987 0.32437 BPC.1 0.0330029 0.0049656 6.646 8.38E-11 *** BPW.1 0.022751 0.0034899 6.519 1.83E-10 *** NPA.1 0.0036844 0.0025294 1.457 0.14589 NPW.1 -0.0037674 0.0023192 -1.624 0.10495 FSP.2 -0.0007562 0.0032574 -0.232 0.81653 FSW.2 -0.0191987 0.0022646 -8.478 3.02E-16 *** SSP.2 NA NA NA NA SSW.2 -0.0126902 0.0031146 -4.074 5.42E-05 *** ACE.2 0.0017076 0.0027408 0.623 0.53357 DBF.2 0.0017989 0.0055318 0.325 0.74517 WNR.2 -0.003155 0.0016141 -1.955 0.05121 . UFE.2 0.0007894 0.0015282 0.517 0.60573 BPC.2 -0.0324298 0.0053581 -6.052 2.93E-09 *** BPW.2 -0.0174061 0.0035668 -4.88 1.46E-06 *** NPA.2 -0.0017918 0.002595 -0.69 0.49023 NPW.2 0.0043482 0.0021816 1.993 0.04683 * この辺の 組み合わせが 重要っぽい
- 54. 54 重回帰分析(統計モデリング)でやりたいこと ?? ~ ?0 + ?1 ?1? + ?2 ?2? + ?3 ?3? + ?4 ?4? + ? ? ? ? ?? + ?? 105 予測値が 具体的に 出せる! 1 変数1 4 変数2 0 変数3 2 変数4 3 変数n このβたちから モデルは成っている 未来において与えることができる説明変数を 入れてやると…?
- 55. Rならpredictメソッドで簡単に予測できる ? ちなみにRでは… – 代表例として以下の関数は共通メソッド ? summary ? predict ? plot – これを理解していれば他のパッケージでも 同様に使いこなせる 55 > plot(cbind(dw$Result, predict(dm.lm, newdata=dw[,-1])), cex=3, col='blue')
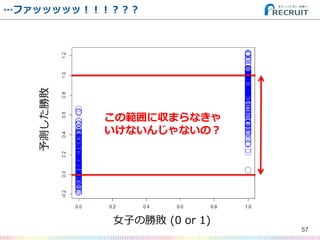
- 56. 予測結果をplotしてみた 56 女子の勝敗 (0 or 1) 予測した勝敗
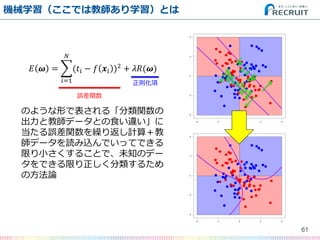
- 57. …ファッッッッッ!!!??? 57 女子の勝敗 (0 or 1) 予測した勝敗 この範囲に収まらなきゃ いけないんじゃないの?
- 61. 機械学習(ここでは教師あり学習)とは 61 ? ? = (?? ? ? ?? )2 ? ?=1 + ??(?) のような形で表される「分類関数の 出力と教師データとの食い違い」に 当たる誤差関数を繰り返し計算+教 師データを読み込んでいってできる 限り小さくすることで、未知のデー タをできる限り正しく分類するため の方法論 誤差関数 正則化項
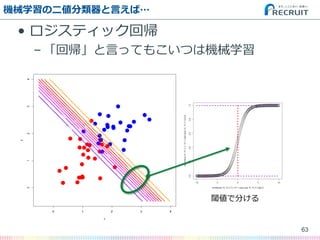
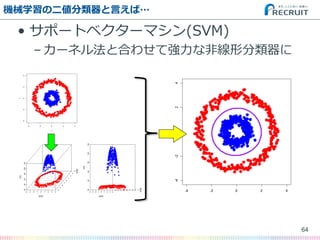
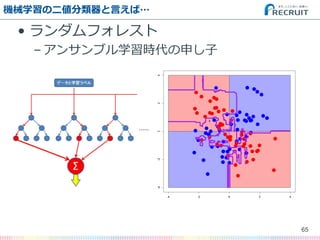
- 62. 機械学習の二値分類器と言えば… ? ロジスティック回帰 – 「回帰」と言ってもこいつは機械学習 ? サポートベクターマシン(SVM) – 汎化性能に優れた老舗分類器 ? ランダムフォレスト – 高性能マシン時代のロックスター 62
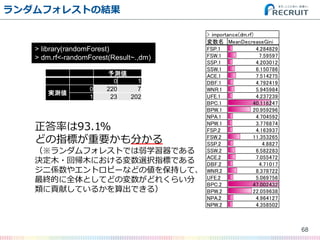
- 66. ロジスティック回帰の結果 66 変数名 偏回帰係数(β ) 標準誤差 z値 p値 有意? (切片) -1.378486 5.064233 -0.272 0.785468 FSP.1 0.116125 0.065947 1.761 0.078258 . FSW.1 0.198896 0.043094 4.615 3.92E-06 *** SSP.1 NA NA NA NA SSW.1 0.290083 0.069708 4.161 3.16E-05 *** ACE.1 -0.040074 0.048374 -0.828 0.40743 DBF.1 -0.136684 0.082271 -1.661 0.096636 . WNR.1 0.074055 0.029644 2.498 0.012485 * UFE.1 -0.007523 0.030277 -0.248 0.803779 BPC.1 0.393523 0.10212 3.854 0.000116 *** BPW.1 0.313412 0.069018 4.541 5.60E-06 *** NPA.1 0.01296 0.042315 0.306 0.759398 NPW.1 -0.014493 0.036409 -0.398 0.690578 FSP.2 -0.065368 0.066044 -0.99 0.322288 FSW.2 -0.263955 0.047725 -5.531 3.19E-08 *** SSP.2 NA NA NA NA SSW.2 -0.247359 0.063257 -3.91 9.22E-05 *** ACE.2 0.026067 0.038823 0.671 0.501937 DBF.2 0.117291 0.084828 1.383 0.166759 WNR.2 -0.032345 0.028113 -1.151 0.249925 UFE.2 -0.024302 0.028906 -0.841 0.40049 BPC.2 -0.329055 0.111769 -2.944 0.003239 ** BPW.2 -0.351452 0.087206 -4.03 5.57E-05 *** NPA.2 -0.036414 0.059266 -0.614 0.538935 NPW.2 0.047514 0.04277 1.111 0.266603 > dm.glm<-glm(Result~.,dm,family=binomial) 予測値 0 1 実測値 0 211 16 1 17 208 正答率は92.7% どの指標が重要かも分かる
- 67. SVMの結果 67 > library(e1071) > dm.svm<-svm(Result~.,dm) 予測値 0 1 実測値 0 210 17 1 19 206 正答率は92.0% どの指標が重要かは分からない (※SVMでは偏回帰係数の計算をするわけで はなく、教師データのひとつひとつから最終 的な分離超平面を算出するため、間接的には 偏回帰係数「のようなもの」を求めることは できても基本的には変数の重要度は不明)
- 68. ランダムフォレストの結果 68 > library(randomForest) > dm.rf<-randomForest(Result~.,dm) 予測値 0 1 実測値 0 220 7 1 23 202 変数名 MeanDecreaseGini FSP.1 4.284829 FSW.1 7.59597 SSP.1 4.203012 SSW.1 6.150786 ACE.1 7.514275 DBF.1 4.792419 WNR.1 5.945984 UFE.1 4.237239 BPC.1 40.116247 BPW.1 20.959296 NPA.1 4.704592 NPW.1 3.776874 FSP.2 4.163937 FSW.2 11.353265 SSP.2 4.8827 SSW.2 6.582283 ACE.2 7.055472 DBF.2 4.71017 WNR.2 8.378722 UFE.2 5.069756 BPC.2 47.002432 BPW.2 22.059638 NPA.2 4.964127 NPW.2 4.358502 > importance(dm.rf) 正答率は93.1% どの指標が重要かも分かる (※ランダムフォレストでは弱学習器である 決定木?回帰木における変数選択指標である ジニ係数やエントロピーなどの値を保持して、 最終的に全体としてどの変数がどれくらい分 類に貢献しているかを算出できる)
- 69. これまでに手に入ったもの ? 結局勝つために重要なのは何? – BPC. 1/2 – つまり「ブレーク機会創出数」 – 言い換えると… ? ブレークし切れなくても良いが ? それだけプレッシャーをかけ続けた方が結果的に ブレークできた回数が少なくても勝てる ? 最も正確に女子の結果を予測できたのは? – ランダムフォレスト – 正答率93.1% ?大体これで良い気もしてきた… 69
- 70. 70 まだ続きがありますよ
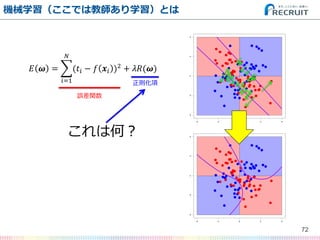
- 72. 機械学習(ここでは教師あり学習)とは 72 ? ? = (?? ? ? ?? )2 ? ?=1 + ??(?) これは何? 誤差関数 正則化項
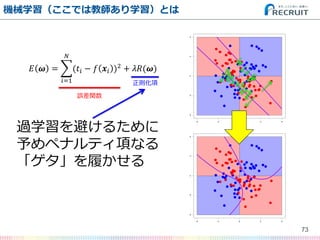
- 73. 機械学習(ここでは教師あり学習)とは 73 ? ? = (?? ? ? ?? )2 ? ?=1 + ??(?) 過学習を避けるために 予めペナルティ項なる 「ゲタ」を履かせる 誤差関数 正則化項
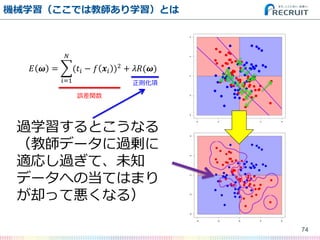
- 74. 機械学習(ここでは教師あり学習)とは 74 ? ? = (?? ? ? ?? )2 ? ?=1 + ??(?) 過学習するとこうなる (教師データに過剰に 適応し過ぎて、未知 データへの当てはまり が却って悪くなる) 誤差関数 正則化項
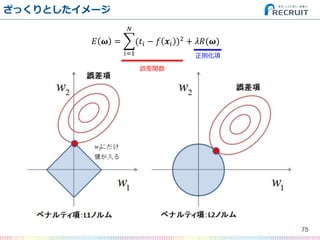
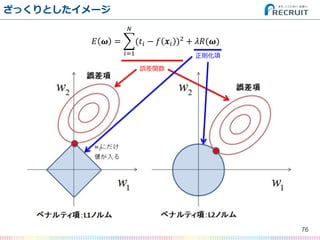
- 75. ざっくりとしたイメージ 75 ? ? = (?? ? ? ?? )2 ? ?=1 + ??(?) 誤差関数 正則化項
- 76. ざっくりとしたイメージ 76 ? ? = (?? ? ? ?? )2 ? ?=1 + ??(?) 誤差関数 正則化項
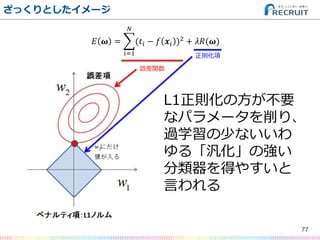
- 77. ざっくりとしたイメージ 77 ? ? = (?? ? ? ?? )2 ? ?=1 + ??(?) 誤差関数 正則化項 L1正則化の方が不要 なパラメータを削り、 過学習の少ないいわ ゆる「汎化」の強い 分類器を得やすいと 言われる
- 78. Rでは{glmnet}パッケージで計算できる 78 > library(glmnet) > dm.cv.glmnet1<-cv.glmnet(as.matrix(dm[,-1]), as.matrix(dm[,1]), family = "binomial", alpha=1) > plot(dm.cv.glmnet1) > coef(dm.cv.glmnet1,s=dm.cv.glmnet1$lambda.min) 25 x 1 sparse Matrix of class "dgCMatrix" 1 (Intercept) 2.500072e-01 FSP.1 4.294774e-02 FSW.1 1.216823e-01 SSP.1 -4.040798e-05 SSW.1 1.553534e-01 ACE.1 . DBF.1 -9.202560e-02 WNR.1 3.813020e-02 UFE.1 -7.980986e-03 BPC.1 3.743690e-01 BPW.1 2.120734e-01 NPA.1 . NPW.1 . FSP.2 -3.175133e-02 FSW.2 -1.625361e-01 SSP.2 . SSW.2 -1.388602e-01 ACE.2 1.365908e-02 DBF.2 4.370369e-02 WNR.2 -2.155338e-02 UFE.2 -8.601338e-04 BPC.2 -3.621961e-01 BPW.2 -2.045213e-01 NPA.2 . NPW.2 1.383386e-02
- 79. L1正則化ロジスティック回帰の結果 79 予測値 0 1 実測値 0 216 11 1 19 206 変数名 偏回帰係数(β ) (切片) 2.50E-01 FSP.1 4.29E-02 FSW.1 1.22E-01 SSP.1 -4.04E-05 SSW.1 1.55E-01 ACE.1 . DBF.1 -9.20E-02 WNR.1 3.81E-02 UFE.1 -7.98E-03 BPC.1 3.74E-01 BPW.1 2.12E-01 NPA.1 . NPW.1 . FSP.2 -3.18E-02 FSW.2 -1.63E-01 SSP.2 . SSW.2 -1.39E-01 ACE.2 1.37E-02 DBF.2 4.37E-02 WNR.2 -2.16E-02 UFE.2 -8.60E-04 BPC.2 -3.62E-01 BPW.2 -2.05E-01 NPA.2 . NPW.2 1.38E-02 正答率は93.4% どの指標が重要かも分かる どの指標が不要かも分かる (※実際にはL2正則化やL1/L2正則化 のミックス “Elastic Net” で分類器を 学習させることでさらに異なる結果を 得ることもできる) ?ベストスコアだ!
- 80. 80 まだ終わっていない!
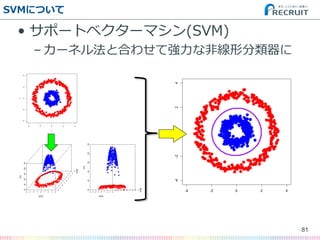
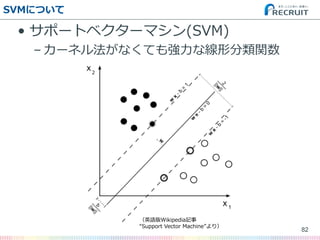
- 82. SVMについて ? サポートベクターマシン(SVM) – カーネル法がなくても強力な線形分類関数 82 (英語版Wikipedia記事 “Support Vector Machine”より)
- 83. 線形SVMの結果… 83 > dm.linear.tune<-tune.svm(Result~., data = dm, kernel = 'linear') > dm.linear.svm<-svm(Result~., dm, kernel = 'linear', cost = dm.linear.tune$best.model$cost, gamma = dm.linear.tune$best.model$gamma) 正答率は93.6% どの指標が重要かは分からないが 予測の正答率はベストスコア! 予測値 0 1 実測値 0 214 13 1 16 209
- 84. 最終的な結論 ? 勝つために重要なのは何? – 依然としてBPC. 1/2(L1正則化ロジスティッ ク回帰の結果より) – つまり「ブレーク機会創出数」 ? ブレークし切れなくても良いが ? それだけプレッシャーをかけ続けた方が結果的に ブレークできた回数が少なくても勝てる ? 最も正確に女子の結果を予測できたのは? – 線形SVM – 正答率93.6% ?これが最終的なベストソリューション 84



















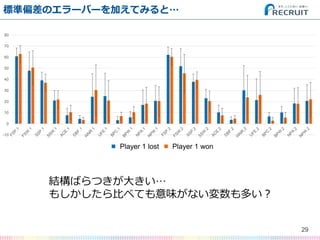







![まずデータを読み込む
46
> dm_raw<-read.table("men.txt",header=T,sep='?t')
> dw_raw<-read.table("women.txt",header=T,sep='?t')
> dm<-dm_raw[,-c(1,2,14,17,18,19,20,21,27,35,36,37,38,39)]
> dw<-dw_raw[,-c(1,2,14,17,18,19,20,21,27,35,36,37,38,39)]
https://github.com/ozt-ca/tjo.hatenablog.samples/tree/master/r_samples/public_lib/jp/exp_uci_datasets/tennis](https://image.slidesharecdn.com/paak20150601-150603074952-lva1-app6892/85/Tech-Lab-Paak-20150601-46-320.jpg)

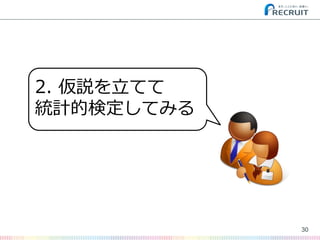
![Rならpredictメソッドで簡単に予測できる
? ちなみにRでは…
– 代表例として以下の関数は共通メソッド
? summary
? predict
? plot
– これを理解していれば他のパッケージでも
同様に使いこなせる
55
> plot(cbind(dw$Result, predict(dm.lm, newdata=dw[,-1])),
cex=3, col='blue')](https://image.slidesharecdn.com/paak20150601-150603074952-lva1-app6892/85/Tech-Lab-Paak-20150601-55-320.jpg)









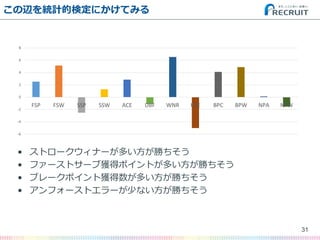
![Rでは{glmnet}パッケージで計算できる
78
> library(glmnet)
> dm.cv.glmnet1<-cv.glmnet(as.matrix(dm[,-1]), as.matrix(dm[,1]), family = "binomial", alpha=1)
> plot(dm.cv.glmnet1)
> coef(dm.cv.glmnet1,s=dm.cv.glmnet1$lambda.min)
25 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) 2.500072e-01
FSP.1 4.294774e-02
FSW.1 1.216823e-01
SSP.1 -4.040798e-05
SSW.1 1.553534e-01
ACE.1 .
DBF.1 -9.202560e-02
WNR.1 3.813020e-02
UFE.1 -7.980986e-03
BPC.1 3.743690e-01
BPW.1 2.120734e-01
NPA.1 .
NPW.1 .
FSP.2 -3.175133e-02
FSW.2 -1.625361e-01
SSP.2 .
SSW.2 -1.388602e-01
ACE.2 1.365908e-02
DBF.2 4.370369e-02
WNR.2 -2.155338e-02
UFE.2 -8.601338e-04
BPC.2 -3.621961e-01
BPW.2 -2.045213e-01
NPA.2 .
NPW.2 1.383386e-02](https://image.slidesharecdn.com/paak20150601-150603074952-lva1-app6892/85/Tech-Lab-Paak-20150601-78-320.jpg)