2014 3 13(テンソル分解の基礎)
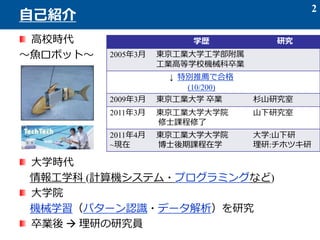
- 2. 高校時代 ~魚ロボット~ 大学時代 情報工学科 (計算機システム?プログラミングなど) 大学院 機械学習(パターン認識?データ解析)を研究 卒業後 ? 理研の研究員 学歴 研究 2005年3月 東京工業大学工学部附属 工業高等学校機械科卒業 ↓ 特別推薦で合格 (10/200) 2009年3月 東京工業大学 卒業 杉山研究室 2011年3月 東京工業大学大学院 修士課程修了 山下研究室 2011年4月 ~現在 東京工業大学大学院 博士後期課程在学 大学:山下研 理研:チホツキ研 2 自己紹介
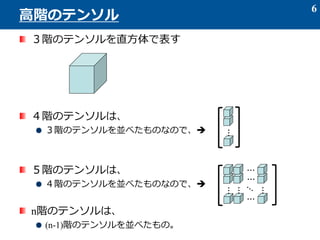
- 5. 多次元配列としてイメージしてみる 0階テンソル: 1階テンソル: 2階テンソル: 3階テンソル: 5 テンソルデータ ベクトル -スカラーを並べたもの 行列 -ベクトルを並べたもの -行列を並べたもの
- 7. 7 テンソルデータの例 時系列データ ? 1階のテンソル (ベクトル) 多チャンネルの時系列データ ? 2階のテンソル (行列) 濃淡画像 カラー画像 ? 2階のテンソル (行列) ? 3階のテンソル (RGB×濃淡画像) カラー動画 ? 4階のテンソル (フレーム×カラー画像)
- 8. N階のテンソルを で表し、 その 成分を または で表す。 足し算(引き算) 同じ大きさの二つのテンソルの和は、 定数cに対するテンソルXの定数倍 cX は、 8 テンソルの計算(1)
- 9. アダマール積(Hadamard product) 同じ大きさの二つのテンソルのアダマール積は、 成分ごとの商(elementwise division) 同じ大きさの二つのテンソルの成分ごとの商は、 クロネッカー積(Kronecker product) 9 テンソルの計算(2)
- 10. 内積とノルム 同じ大きさの二つのテンソルの内積は、 X = Y のとき、フロベニウスノルムになる 10 テンソルの計算(3)
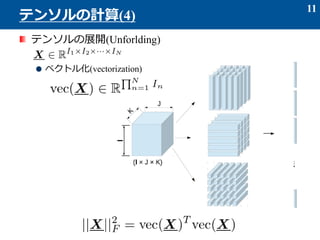
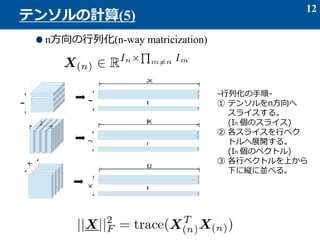
- 12. n方向の行列化(n-way matricization) 12 テンソルの計算(5) -行列化の手順- ① テンソルをn方向へ スライスする。 (In 個のスライス) ② 各スライスを行ベク トルへ展開する。 (In 個のベクトル) ③ 各行ベクトルを上から 下に縦に並べる。
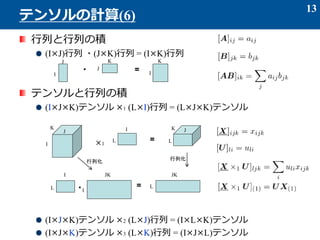
- 13. 行列と行列の積 (I×J)行列 ?(J×K)行列 = (I×K)行列 テンソルと行列の積 (I×J×K)テンソル ×1 (L×I)行列 = (L×J×K)テンソル (I×J×K)テンソル ×2 (L×J)行列 = (I×L×K)テンソル (I×J×K)テンソル ×3 (L×K)行列 = (I×J×L)テンソル 13 テンソルの計算(6) =? I J J K K I I J K ×1 I L = L JK I L I = JK L JK 行列化 行列化 ?
- 14. 3階テンソルと3つの行列との積 14 テンソルの計算(7) I J K ×1 L = L MN ×2 M ×3 N I J K I L I = JK L MN ? ? MN JK 行列化で表記すると =IJK LMN? ベクトル化で表記すると IJK LMN
- 19. 全部同じモデルを指す CP: canonical polyadic decomposition PARAFAC: pararell factor analysis CANDECOMP: canonical decomposition ここでは、CPモデルとよびます。 1ランクテンソル N個のベクトルの外積で表せるN階テンソル CPモデル(3階テンソル) Rランクへの近似モデルになっている 19 CPモデル
- 21. 評価基準 a,b,c のノルムは一意に決まらない 任意の実数dに対して, a? a/d, b?b*d としてもよい a,b,c のノルムを正規化 21 CP分解のための評価基準 特異値の テンソル版
- 23. 入力: X, R 初期化:B, C (各列のノルムは1) 収束するまで繰り返し (r=1,…,R) (r=1,…,R) (r=1,…,R) (r=1,…,R) 出力: A, B, C, Λ 23 CP分解のアルゴリズムまとめ
- 25. Tuckerモデルの行列化(3階テンソル) Tuckerモデルのベクトル化 25 Tuckerモデルの展開 I R1 I = JK R2R3 JK A R1 R2R3 (C × B)〇 T G(1) [Tuck](1) (C × B × A)〇 〇 =IJK IJK R1R2R3 R1R2R3?
- 26. 評価基準 G,A,B,C は一意に決まらない A, B, C に正規直交制約を加える(これでも一意にはならない…) 目的関数Lについて見ていく 26 Tucker分解のための評価基準 ?この目的関数を 関数L とおく ?
- 29. 入力: X, R1, R2, R3 初期化ステップ Repeat(収束まで) End 出力: G, A, B, C 29 Tucker分解のアルゴリズムまとめ HOSVD HOOI
- 31. 解の一意性の向上 目的にあった特徴を抽出したい 例: Textデータ(ヒストグラム)、確率密度関数は必ず非負であり、 それらを構成する基底(特徴)ベクトルもまた非負であるはず。 例: 物理的要因でスパース性、スムース性を仮定して良い場合、( スムースな自然画像、一般に疎なスペクトルなど) 例: それぞれが独立な特徴ベクトルを抽出したい ノイズや、無駄な因子をできるだけ取り除きたい 制約によっては、ノイズに対する頑健性を向上できる 31 なぜ、制約が必要なのか? 解の領域 解の領域制約
- 33. スパースとは、 ベクトルの成分のほとんどの値が 0 のような状態をいう 例: a = [0 0 0 0 5 0 0 0 -1 4 0 0 0 0 0 0 -9 0 0 0 0] スパース性を得るための制約 l1-ノルムの最小化が良く用いられる l1-ノルム 評価基準: LASSO と呼ばれる 二次の目的関数+L1ノルムの最小化 λ:正則化パラメータ 弱い成分をつぶして、主要な成分のみを残す 33 スパース制約 l1ノルムの等高線 目的関数の等高線
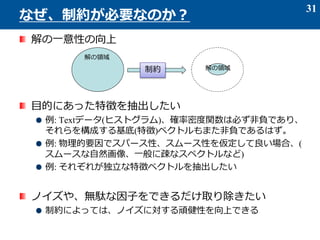
- 34. スムース性 ベクトルの隣り合う成分の値の差が小さい 例: a = [0 -3 9 0 5 15 0 0 0 0 1 1 0 -1 -1 1 2] 良く用いられる評価基準(fused lasso, total variation) 他にも、Aをスムースな基底関数の線形結合としてモデル 化する方法が提案されている A=ΦW ノイズに対する頑健性が得られる 34 スムース制約 スムースでない スムース
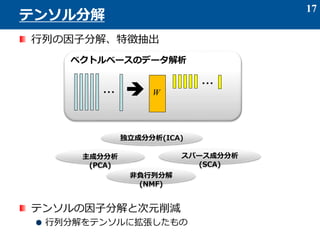
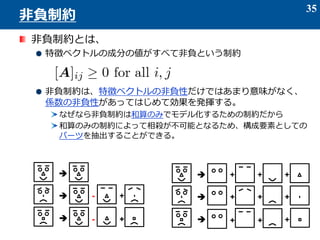
- 36. スパース?スムース?非負制約などを付加したさまざまな 拡張が提案されている。 スパースCP分解[Allen, 2012] スパースTucker分解 非負CP分解 非負Tucker分解[Kim&Choi, 2007][Phan&Cichoki, 2008,2009,2011] スムース非負CP分解[Yokota et al, 2015] スムース非負Tucker分解[Tokota et al, 2015] 行列分解の多様な技術をテンソル分解に拡張したい 主成分分析(PCA)、スパースPCA、スパース&スムースPCA 非負行列分解(NMF)、スパースNMF、スムースNMF 独立成分分析(ICA) 共通個別因子分析など 36 CP?Tucker分解のさまざまな拡張
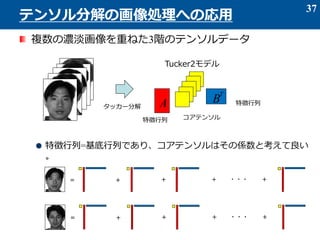
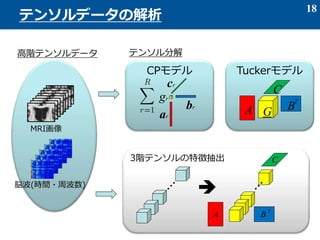
- 37. 複数の濃淡画像を重ねた3階のテンソルデータ 特徴行列=基底行列であり、コアテンソルはその係数と考えて良い 。 37 テンソル分解の画像処理への応用 A B T タッカー分解 Tucker2モデル 特徴行列 特徴行列 コアテンソル = + + + +??? = + + + +???
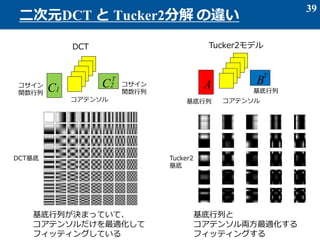
- 39. 39 二次元DCT と Tucker2分解 の違い A B T Tucker2モデル 基底行列 基底行列 コアテンソル C1 C2 T コサイン 関数行列 コサイン 関数行列 コアテンソル DCT 基底行列が決まっていて、 コアテンソルだけを最適化して フィッティングしている 基底行列と コアテンソル両方最適化する フィッティングする DCT基底 Tucker2 基底
- 40. もし、NMF/NTFによって顔画像のパーツが的確に学習さ れていれば、パーツの組み合わせによって顔画像を構成で きる。 ノイズを付加された顔画像を、構成モデルで再構成する事を考え る。再構成された画像は基底行列が張る空間に限定されるため、 ノイズ除去に利用できる。 張る空間の次元が小さいとまったく別の(平均的な)顔になる… 40 非負テンソル分解による顔画像の再構成 ノイズ付加 NMF Smooth NMF NTF Smooth NTF
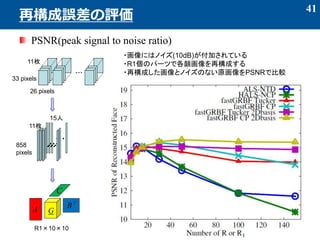
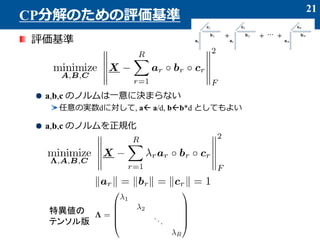
- 41. PSNR(peak signal to noise ratio) 41 再構成誤差の評価 11枚 33 pixels 26 pixels GA C B T ??? 15人 ??? ????????? 11枚 858 pixels R1×10×10 ?画像にはノイズ(10dB)が付加されている ?R1個のパーツで各顔画像を再構成する ?再構成した画像とノイズのない原画像をPSNRで比較
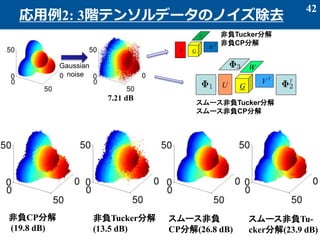
- 42. 42 応用例2: 3階テンソルデータのノイズ除去 7.21 dB 非負CP分解 (19.8 dB) 非負Tucker分解 (13.5 dB) スムース非負 CP分解(26.8 dB) スムース非負Tu- cker分解(23.9 dB) Gaussian noise GA C B T GU W V T T 非負Tucker分解 非負CP分解 スムース非負Tucker分解 スムース非負CP分解
















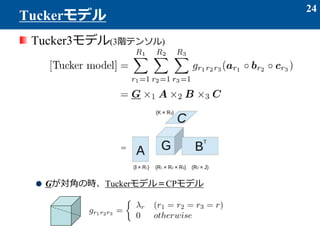

(C × B × A)〇 〇
=IJK IJK
R1R2R3
R1R2R3?](https://image.slidesharecdn.com/2014313-150415013523-conversion-gate01/85/2014-3-13-25-320.jpg)




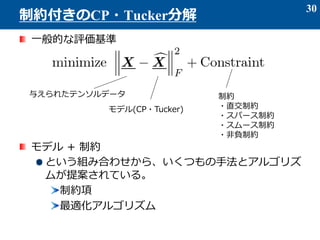
![スパースとは、
ベクトルの成分のほとんどの値が 0 のような状態をいう
例: a = [0 0 0 0 5 0 0 0 -1 4 0 0 0 0 0 0 -9 0 0 0 0]
スパース性を得るための制約
l1-ノルムの最小化が良く用いられる
l1-ノルム
評価基準: LASSO と呼ばれる
二次の目的関数+L1ノルムの最小化
λ:正則化パラメータ
弱い成分をつぶして、主要な成分のみを残す
33
スパース制約
l1ノルムの等高線
目的関数の等高線](https://image.slidesharecdn.com/2014313-150415013523-conversion-gate01/85/2014-3-13-33-320.jpg)
![スムース性
ベクトルの隣り合う成分の値の差が小さい
例: a = [0 -3 9 0 5 15 0 0 0 0 1 1 0 -1 -1 1 2]
良く用いられる評価基準(fused lasso, total variation)
他にも、Aをスムースな基底関数の線形結合としてモデル
化する方法が提案されている
A=ΦW
ノイズに対する頑健性が得られる
34
スムース制約
スムースでない スムース](https://image.slidesharecdn.com/2014313-150415013523-conversion-gate01/85/2014-3-13-34-320.jpg)
![スパース?スムース?非負制約などを付加したさまざまな
拡張が提案されている。
スパースCP分解[Allen, 2012]
スパースTucker分解
非負CP分解
非負Tucker分解[Kim&Choi, 2007][Phan&Cichoki, 2008,2009,2011]
スムース非負CP分解[Yokota et al, 2015]
スムース非負Tucker分解[Tokota et al, 2015]
行列分解の多様な技術をテンソル分解に拡張したい
主成分分析(PCA)、スパースPCA、スパース&スムースPCA
非負行列分解(NMF)、スパースNMF、スムースNMF
独立成分分析(ICA)
共通個別因子分析など
36
CP?Tucker分解のさまざまな拡張](https://image.slidesharecdn.com/2014313-150415013523-conversion-gate01/85/2014-3-13-36-320.jpg)