ITC_principle02_japanese_ver.1.0
- 1. 120924 ver. 1.0 Ą╚╬┬Ą╬Č©ą═¤ß£yČ©Ę©(ITC)ż╬Ė┼šō ó┌ ? Ż▒īØŻ▓ Č└┴óĮY║Ž▓┐╬╗źŌźŪźļĮŌ╬÷╩Į for ITC Presented by Satoshi Kume Osaka Prefecture University
- 2. Ż▒īØŻ▓ Č└┴óĮY║Ž▓┐╬╗źŌźŪźļĮŌ╬÷╩Į for ITC 1īØ2 ?Č└┴óĮY║ŽźŌźŪźļ (1:1 ?Binding ?at ?each ?site) ? Ka1 ? P ? ? ?+ ? ? ?L1 ? PL1 ? (1) ? Kd1 ? Ka2 ? P ? ? ?+ ? ? ?L2 ? PL2 ? (2) ? Kd2 ? [PL1 ] [PL1 ] K a1 = = [Pf ][Lf ] ([Pt ] ? [PL1 ])[Lf ] Ka: ĮY║ŽČ©╩², Kd: ĮŌļxČ©╩², [Pf]: ▀[ļxź┐ź¾źčź»┘|ØŌČ╚, [Pt]: Štź┐ź¾źčź»┘|ØŌČ╚, [Lf]: ▀[ļxźĻź¼ź¾ź╔ØŌČ╚, [Lt]: ŠtźĻź¼ź¾ź╔ØŌČ╚ [PL]: ź┐ź¾źčź»┘|-źĻź¼ź¾ź╔č}║Ž╠ÕØŌČ╚
- 3. ? K a1 ([Pt ] ? [PL1 ])[Lf ] = [PL1 ] ? K a1[Pt ][Lf ] ? [PL1 ][Lf ] = [PL1 ] Każ“Kdż╦ēõōQż╣żļ K a1[Pt ][Lf ] [Pt ][Lf ] ? [PL1 ] = = Ć K a1[Lf ] +1 ?? 1 ?? K d1?? [Lf ] +1?? ?? K d1 ?? [Pt ][Lf ] ? [PL1 ] = [Lf ] + K d1 Ć ═¼śöż╦żĘżŲ [PL2 ] [Pt ][Lf ] K a2 = ? [PL2 ] = Ć [Pf ][Lf ] [Lf ] + K d2
- 4. │ó│┘żŽęįŽ┬ż╬żĶż”ż╦▒ĒżĄżņżļ [Lt ] = [Lf ] + [PL1 ] + [PL2 ] [Pt ][Lf ] [Pt ][Lf ] ? [Lt ] = [Lf ] + + [Lf ] + K d1 [Lf ] + K d2 Ć 3 2 ? [Lf ] + a[Lf ] + b[Lf ] + c = 0 éS╩²aĪóbĪócżŽęįŽ┬ż╬żĶż”ż╦ż╩żļ Ć ?? a = K d1 + K d2 + 2[Pt ] ? [Lt ] ?? Ć ??b = (K d1 + K d2 )([Pt ] ? [Lt ]) + K d1K d2 ?? ?? c = ?K d1K d2 [Lt ]
- 5. a [Lf ] = u ? ż╚ż¬ż» 3 3 2 ?? a ?? ?? a ?? ?? a ?? ? ?? u ? ?? + a?? u ? ?? + b?? u ? ?? + c = 0 Ć ?? 3 ?? ?? 3 ?? ?? 3 ?? ╔Žėøż╬╩Įż“š╣ķ_ż╣żļ ?? 3 2 2 1 2 1 2 2 2 1 3 ?? ? ?? u ? au + a u ? au + a u ? a ?? Ć ?? 3 9 3 9 27 ?? ?? 2 2 1 2 ?? ?? a ?? +a?? u ? au + a ?? + b?? u ? ?? + c = 0 ?? 3 9 ?? ?? 3 ??
- 6. 3 ?? a 2 ?? ?? 2 3 1 ?? ? u = ?? ? b??u + ?? ? a + ab ? c ?? ?? 3 ?? ?? 27 3 ?? ?? a 2 ?? p= ?b ?? 3 ż╚ż¬ż» 3 u = pu + q Ć ??q = ? 2 a 3 + 1 ab ? c ?? 27 3 ż▐ż┐ ?? 2 a 2 1 2 ?? p = 3”┴ 2 ?? 3”┴ = Ć ?b ? ”┴ = a ? 3b ?? ż╚ż¬ż»ż╚ ?? 3 3 ?? q = ”┴ 2”┬ ?? 2 2 3 1 ”┴ ”┬ = ? a + ab ? c ?? 27 3 3 2 2 ? u = 3”┴ u + ”┴ ”┬
- 7. żĄżķż╦ u = 2”┴ cos ”╚ ż╚ż¬ż» 3 2 2 (2”┴ cos”╚ ) = 3”┴ (2”┴ cos”╚ ) + ”┴ ”┬ 3 3 3 2 Ć ? 8”┴ cos ”╚ = 6”┴ cos ”╚ + ”┴ ”┬ 3 3 ”┬ Ć ? cos ”╚ = cos ”╚ + 4 8”┴ Ć ╚²▒ČĮŪż╬╣½╩ĮżĶżĻ ?? 3 1 ?? 3 ”┬ ? ?? cos ”╚ + cos 3”╚ ?? = cos ”╚ + Ć ?? 4 4 ?? 4 8”┴ ”┬ 1 ”┬ ? cos 3”╚ = ? ”╚ = arccos 2”┴ 3 2”┴
- 8. ▒½żŪĮŌż»ż╚ęįŽ┬ż╬ĮŌż¼Ū¾ż▐żļ ?? ?? 1 ”┬ ?? ?? u1 = 2”┴ cos”╚ = 2”┴ cos?? arccos ?? ?? ?? 3 2”┴ ?? ?? ?? 2 ?? ? ?? u2 = 2”┴ cos??”╚ + ”ą ?? ?? ?? 3 ?? ?? ?? 4 ?? ?? u3 = 2”┴ cos??”╚ + ”ą ?? ?? ?? 3 ?? 2 3 1 ”┬ ?2a 3 + 9ab ? 27c ”┴ 2 ”┬ = ? a + ab ? c ? = 27 3 2”┴ 54 ”┴ 3 Ć 3 ”┬ ?2a + 9ab ? 27c 3 ”┬ ?2a + 9ab ? 27c ? = 3 ? = 2”┴ ?? 1 2 ?? 2”┴ 2 ( a ? 3b) 2 3 Ć 54?? a ? 3b ?? ?? 3 ??
- 9. żĘż┐ż¼ż├żŲ 3 1 ?2a + 9ab ? 27c ”╚ = arccos 3 2 ( a ? 3b) 2 3 ?? ?? 3 2 2 ?? 1 ?2a + 9ab ? 27c ?? ? u1 = a ? 3b cos?? arccos ?? Ć 3 ?? 3 3 2 ( a ? 3b) ?? 2 ?? ?? a [Lf ] = u ? ż╦┤·╚ļż╣żļ 3 ?? ?? 2 2 ?? 1 ?2a 3 + 9ab ? 27c ?? a [Lf ] = a ? 3b cos?? arccos ?? ? 3 3 ?? 3 3 2 ( a ? 3b) ?? 2 ?? ??
- 10. ░┌│ó┤┌▒šż“ęįŽ┬ż╬╩Įż╦Ą▒żŲżŽżßżļ(╩Ī┬į) [Pt ][Lf ] [Pt ][Lf ] [PL1 ] = ż¬żĶżė [PL2 ] = [Lf ] + K d1 [Lf ] + K d2 Q = V0 ([PL1]”żH1+[PL2]”żH2)ż╦┤·╚ļż╣żļ ?? [Pt ][Lf ]”żH1 [Pt ][Lf ]”żH 2 ?? Q = V0 ?? + ?? Ć ?? [Lf ] + K d1 [Lf ] + K d 2 ?? The pertinent calculated heat effect for the i inject is ”żV (i) ?? Q(i) + Q(i ?1) ?? ”żQ(i) = Q(i) ? Q(i ?1) + ?? ?? Ć V0 ?? 2 ?? MolØŌČ╚ż╦čaš² ”żQ(i) ”żQi = Ć [V (i) ? V (i ?1)]Lsyr


![Ż▒īØŻ▓ Č└┴óĮY║Ž▓┐╬╗źŌźŪźļĮŌ╬÷╩Į for ITC
1īØ2
?Č└┴óĮY║ŽźŌźŪźļ (1:1
?Binding
?at
?each
?site)
?
Ka1
?
P
?
?
?+
?
?
?L1
? PL1
? (1)
?
Kd1
?
Ka2
?
P
?
?
?+
?
?
?L2
? PL2
? (2)
?
Kd2
?
[PL1 ] [PL1 ]
K a1 = =
[Pf ][Lf ] ([Pt ] ? [PL1 ])[Lf ]
Ka: ĮY║ŽČ©╩², Kd: ĮŌļxČ©╩², [Pf]: ▀[ļxź┐ź¾źčź»┘|ØŌČ╚,
[Pt]: Štź┐ź¾źčź»┘|ØŌČ╚, [Lf]: ▀[ļxźĻź¼ź¾ź╔ØŌČ╚, [Lt]: ŠtźĻź¼ź¾ź╔ØŌČ╚
[PL]: ź┐ź¾źčź»┘|-źĻź¼ź¾ź╔č}║Ž╠ÕØŌČ╚](https://image.slidesharecdn.com/itcprinciple02ver-1-0-120924022551-phpapp01/85/ITC_principle02_japanese_ver-1-0-2-320.jpg)
![? K a1 ([Pt ] ? [PL1 ])[Lf ] = [PL1 ]
? K a1[Pt ][Lf ] ? [PL1 ][Lf ] = [PL1 ]
Każ“Kdż╦ēõōQż╣żļ
K a1[Pt ][Lf ] [Pt ][Lf ]
? [PL1 ] = =
Ć K a1[Lf ] +1 ?? 1 ??
K d1?? [Lf ] +1??
?? K d1 ??
[Pt ][Lf ]
? [PL1 ] =
[Lf ] + K d1
Ć ═¼śöż╦żĘżŲ
[PL2 ] [Pt ][Lf ]
K a2 = ? [PL2 ] =
Ć [Pf ][Lf ] [Lf ] + K d2](https://image.slidesharecdn.com/itcprinciple02ver-1-0-120924022551-phpapp01/85/ITC_principle02_japanese_ver-1-0-3-320.jpg)
![│ó│┘żŽęįŽ┬ż╬żĶż”ż╦▒ĒżĄżņżļ
[Lt ] = [Lf ] + [PL1 ] + [PL2 ]
[Pt ][Lf ] [Pt ][Lf ]
? [Lt ] = [Lf ] + +
[Lf ] + K d1 [Lf ] + K d2
Ć
3 2
? [Lf ] + a[Lf ] + b[Lf ] + c = 0
éS╩²aĪóbĪócżŽęįŽ┬ż╬żĶż”ż╦ż╩żļ
Ć
?? a = K d1 + K d2 + 2[Pt ] ? [Lt ]
??
Ć ??b = (K d1 + K d2 )([Pt ] ? [Lt ]) + K d1K d2
??
?? c = ?K d1K d2 [Lt ]](https://image.slidesharecdn.com/itcprinciple02ver-1-0-120924022551-phpapp01/85/ITC_principle02_japanese_ver-1-0-4-320.jpg)
![a
[Lf ] = u ? ż╚ż¬ż»
3
3 2
?? a ?? ?? a ?? ?? a ??
? ?? u ? ?? + a?? u ? ?? + b?? u ? ?? + c = 0
Ć ?? 3 ?? ?? 3 ?? ?? 3 ??
╔Žėøż╬╩Įż“š╣ķ_ż╣żļ
?? 3 2 2 1 2 1 2 2 2 1 3 ??
? ?? u ? au + a u ? au + a u ? a ??
Ć ?? 3 9 3 9 27 ??
?? 2 2 1 2 ?? ?? a ??
+a?? u ? au + a ?? + b?? u ? ?? + c = 0
?? 3 9 ?? ?? 3 ??](https://image.slidesharecdn.com/itcprinciple02ver-1-0-120924022551-phpapp01/85/ITC_principle02_japanese_ver-1-0-5-320.jpg)
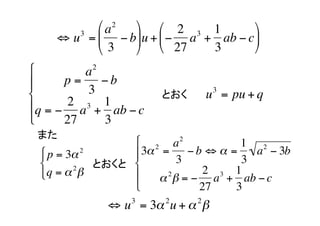


![żĘż┐ż¼ż├żŲ
3
1 ?2a + 9ab ? 27c
”╚ = arccos
3 2 ( a ? 3b)
2 3
?? ??
3
2 2 ?? 1 ?2a + 9ab ? 27c ??
? u1 = a ? 3b cos?? arccos ??
Ć 3 ?? 3 3
2 ( a ? 3b) ??
2
?? ??
a
[Lf ] = u ? ż╦┤·╚ļż╣żļ
3
?? ??
2 2 ?? 1 ?2a 3 + 9ab ? 27c ?? a
[Lf ] = a ? 3b cos?? arccos ?? ? 3
3 ?? 3 3
2 ( a ? 3b) ??
2
?? ??](https://image.slidesharecdn.com/itcprinciple02ver-1-0-120924022551-phpapp01/85/ITC_principle02_japanese_ver-1-0-9-320.jpg)
![░┌│ó┤┌▒šż“ęįŽ┬ż╬╩Įż╦Ą▒żŲżŽżßżļ(╩Ī┬į)
[Pt ][Lf ] [Pt ][Lf ]
[PL1 ] = ż¬żĶżė
[PL2 ] =
[Lf ] + K d1 [Lf ] + K d2
Q = V0 ([PL1]”żH1+[PL2]”żH2)ż╦┤·╚ļż╣żļ
?? [Pt ][Lf ]”żH1 [Pt ][Lf ]”żH 2 ??
Q = V0 ?? + ??
Ć
?? [Lf ] + K d1 [Lf ] + K d 2 ??
The pertinent calculated heat effect for the i inject is
”żV (i) ?? Q(i) + Q(i ?1) ??
”żQ(i) = Q(i) ? Q(i ?1) + ?? ??
Ć V0 ?? 2 ??
MolØŌČ╚ż╦čaš²
”żQ(i)
”żQi =
Ć
[V (i) ? V (i ?1)]Lsyr](https://image.slidesharecdn.com/itcprinciple02ver-1-0-120924022551-phpapp01/85/ITC_principle02_japanese_ver-1-0-10-320.jpg)