狠狠撸

三角関数
レムニスケート関数
Jacobi の楕円関数
テータ関数
楕円関数とおもしろい応用
@matsumoring
2015.9.22
@matsumoring 楕円関数とおもしろい応用

三角関数
テータ関数
三角関数
De?nition.
“円周率” π を
π
2
:=
∫ 1
0
dx
√
1 ? x2
で定める．また,
x = sin u
def.
?? u =
∫ x
0
dx
√
1 ? x2
(
?1 ≤ x ≤ 1
?π/2 ≤ u ≤ π/2
)
とする．

三角関数
テータ関数
x2
+ y2
= 1 の微分を考えて
x + y
dy
dx
= 0, よって
dy
dx
= ?
x
y
? u =
∫ x
0
√
1 +
(
dy
dx
)2
dx
=
∫ x
0
√
y2 + x2
y2
dx
=
∫ x
0
dx
y
=
∫ x
0
dx
√
1 ? x2
.
? 幾何学的に R 全体に拡張する．
x
y
0 1x
+?
u

三角関数
テータ関数
Proposition.
sin(u + 2π) = sin u,
sin(?u) = ? sin u.
Proof.
後半のみ示す．
∫ ?y0
0
dx
√
1 ? x2
=
(x=?y)
?
∫ y0
0
dy
√
1 ? y2
=: ?u
∴ sin(?u) = ?y0 = ? sin u.

三角関数
テータ関数
Theorem.
u, v を十分小さくとれば次式が成立；
sin(u + v) = sin u
√
1 ? sin2
v + sin v
√
1 ? sin2
u
Proof.
z = x
√
1 ? y2 + y
√
1 ? x2 とおく． z :十分小を ?x. ここで
x 0 → x
y z → y
に注意．
dz =
(√
1 ? y2 ?
xy
√
1 ? x2
)
dx +
(
?
xy
√
1 ? y2
+
√
1 ? x2
)
dy = 0
∴
(√
(1 ? x2)(1 ? y2) ? xy
)
(
dx
√
1 ? x2
+
dy
√
1 ? y2
)
= 0.

三角関数
テータ関数
Proof (Cont.)
dx
√
1 ? x2
+
dy
√
1 ? y2
= 0
?
∫ x
0
dx
√
1 ? x2
+
∫ y
z
dy
√
1 ? y2
= 0
?
∫ x
0
dx
√
1 ? x2
=: u
+
∫ y
0
dy
√
1 ? y2
=: v
=
∫ z
0
dz
√
1 ? z2
.
すなわち次が成り立つ．
sin(u + v) = z = x
√
1 ? y2 + y
√
1 ? x2.
ここで x = sin u, y = sin v より証明は完了する．

三角関数
テータ関数
cos 関数を次のようにして定める．
De?nition.
cos u := sin
(π
2
? u
)
.
ここで次は明らか．
Proposition.
cos2
u + sin2
u = 1.
Theorem.
sin(u + v) = sin u cos v + cos u sin v.
Question.
sin
π
6
を求めよ．

三角関数
テータ関数
De?nition.
“レムニスケート周率” ? を
?
2
:=
∫ 1
0
dx
√
1 ? x4
で定める．また，
x = sl u
def.
?? u =
∫ x
0
dx
√
1 ? x4
(
?1 ≤ x ≤ 1
??/2 ≤ u ≤ ?/2
)
とする．

三角関数
テータ関数
三角関数のときと同様に r2
= cos 2θ の微
分を考える．rdr = ? sin 2θ dθ より，
dθ
dr
= ?
r
sin 2θ
= ?
r
√
1 ? r4
? u =
∫ r
0
√
1 +
(
r
dθ
dr
)2
dr
=
∫ r
0
√
1 ? r4 + r4
1 ? r4
dr
=
∫ r
0
dr
√
1 ? r4
.
? 幾何学的に R 全体に拡張する．
x
y
1?1
u
r
+
?

三角関数
テータ関数
三角関数のときと同様に考えて
Proposition.
sl(u + 2?) = sl u,
sl(?u) = ? sl u.
Theorem.
u, v を十分小さくとれば次式が成立；
sl(u + v) =
sl u
√
1 ? sl4
v + sl v
√
1 ? sl4
u
1 + sl2
u sl2
v
.
が成立する．

三角関数
テータ関数
cl 関数を次のようにして定める．
De?nition.
cl u := sl
(?
2
? u
)
.
Proposition.
cl2
u + cl2
u sl2
u + sl2
u = 1.
Theorem.
sl(u + v) =
sl u cl v + cl u sl v
1 ? sl u cl u sl v cl v
.
Question.
sl
?
6
を求めよ．

三角関数
テータ関数
De?nition.
v ∈ R, i =
√
?1 とする．
sl iv := i sl v, cl iv :=
1
cl v
.
∵ ∫ iy0
0
dx
√
1 ? x4
=
(x=iy)
i
∫ y0
0
dy
√
1 ? y4
=: iv
より
sl iv = iy0 = i sl v,
cl iv =
√
1 ? sl2
iv
1 + sl2
iv
=
√
1 + sl2
v
1 ? sl2
v
=
1
cl v
.

三角関数
テータ関数
加法定理とあわせて，
De?nition.
u, v ∈ R とする．
sl(u + iv) :=
sl u cl iv + cl u sl iv
1 ? sl u cl u sl iv cl iv
.
Proposition.
sl(u + 2?i) = sl u (?u ∈ C).
Proof.
u = a + bi, (a, b ∈ R) とおけば
sl(u + 2?i) = sl (a + (b + 2?)i)
= sl(a + bi) = sl u.

三角関数
テータ関数
De?nition.
R 上独立な 2 つの周期を持つ有理型関数を楕円関数という．
Remark.
sl の基本周期は実は 2? と ? + ?i である．

三角関数
テータ関数
De?nition.
a, b > 0, a0 := a, b0 := b
an+1 :=
an + bn
2
, bn+1 :=
√
anbn
とする．このとき，
M(a, b) := lim
n→∞
an = lim
n→∞
bn
と定め，a と b の “算術幾何平均” とよぶ．
Theorem.
M(1,
√
2) =
π
?
.

三角関数
テータ関数
単振り子
l
mgt = 0
θ
E =
1
2
m
(
l ˙θ
)2
+ mgl (1 ? cos θ)
= mgl (1 ? cos θ0)
(ただし ?θ0 ≤ θ ≤ θ0.)
ここで m = g = l = 1 とする．

三角関数
テータ関数
1
2
˙θ2
+ (1 ? cos θ) = 1 ? cos θ0
?
1
2
˙θ2
+ 2 sin2 θ
2
= 2 sin2 θ0
2
? ˙θ2
= 4
(
sin2 θ0
2
? sin2 θ
2
)
k := sin
θ0
2
= 4k2
(
1 ? sin2
φ
)
k sin φ := sin
θ
2
= 4k2
cos2
φ k cos φ dφ =
1
2
cos
θ
2
dθ
∴
dθ
dt
= 2k cos φ =
1
2
√
1 ? k2 sin2
φ dθ
dθ =
2k cos φ dφ
√
1 ? k2 sin2
φ

三角関数
テータ関数
t =
∫ t
0
dt =
∫ θ
0
dθ
2k cos φ
=
∫ φ
0
dφ
√
1 ? k2 sin2
φ
=
∫ x
0
dx
√
(1 ? x2)(1 ? k2x2)
x = sin φ
dx = cos φ dφ
=
√
1 ? x2 dφ
θ 0 → θ0
φ 0 → π/2
x 0 → 1

三角関数
テータ関数
De?nition.
K(k) = K :=
∫ π/2
0
dφ
√
1 ? k2 sin2
φ
=
∫ 1
0
dx
√
(1 ? x2)(1 ? k2x2)
と定める．ここで
K : 第一種完全楕円積分，k : 母数，k′
:=
√
1 ? k2 : 補母数という．
De?nition.
x = sn(u, k) = sn u
def.
?? u =
∫ x
0
dx
√
(1 ? x2)(1 ? k2x2)
また，
cn u :=
√
1 ? sn2 u,
dn u :=
√
1 ? k2 sn2 u.
※今までと同様に R 全体に
拡張しておく．

三角関数
テータ関数
定義からすぐ分かること
k → 0 sn u → sin u,
k = i sn u = sl u, cl u = cn u/ dn u
k → 1 sn u → tanh u
Proposition.
sn(?u) = ? sn u, sn(u + 4K) = sn u,
cn(?u) = cn u, cn(u + 4K) = cn u,
dn(?u) = dn u, dn(u + 2K) = dn u.
u 0 K 2K 3K 4K
dn u 1 k′
1 k′
1

三角関数
テータ関数
Theorem. (sn の加法定理)
sn(u + v) =
sn u cn v dn v + sn v cn u dn u
1 ? k2 sn2 u sn2 v
Theorem. (Landen 変換)
k1 :=
1 ? k′
1 + k′
とおく．このとき
sn
(
(1 + k′
)u, k1
)
= (1 + k′
)
sn(u, k) cn(u, k)
dn(u, k)
が成立．

三角関数
テータ関数
Proposition.
K =
2
1 + k′
K1
(
K1 := K(k1)
)
Proof.
Landen 変換で u = K とすると
sn
(
(1 + k′
)K, k1
)
= (1 + k′
)
sn(K, k) cn(K, k)
dn(K, k)
= 0 (∵ cn(K, k) = 0, dn(K, k) ?= 0).
よって (1 + k′
)K = 2nK であるが，実は n = 1．

三角関数
テータ関数
Theorem.
a, b > 0, k′
:= b/a とする．このとき
M(1, k′
) =
π
2K
.
Proof.
k′
1 :=
√
1 ? k2
1 とおけば，
k′
1 =
√
1 ?
(
1 ? k′
1 + k′
)2
=
√
(1 + k′)2 ? (1 ? k′)2
(1 + k′)2
=
√
4k′
(1 + k′)2
=
2
√
k′
1 + k′
.

三角関数
テータ関数
Proof (Cont.)
つまり
k′
1 =
2
√
k′
1 + k′
.
ここで k′
= b/a としたので
k′
1 =
2
√
b/a
1 + (b/a)
=
2
a + b
√
ab
=
b1
a1
.

三角関数
テータ関数
Proof (Cont.)
ここで I(a, b) :=
∫ π/2
0
dφ
√
a2 cos2 φ + b2 sin2
φ
と書くと
K =
∫ π/2
0
dφ
√
1 ? k2 sin2
φ
=
∫ π/2
0
dφ
√
cos2 φ + (1 ? k2) sin2
φ
= I(1, k′
) = I
(
1,
b
a
)
= aI(a, b)
同様に K1 = a1I(a1, b1) が分かる．

三角関数
テータ関数
Proof (Cont.)
Landen 変換の後の Proposition より
K =
2
1 + k′
K1 =
2
1 + (b/a)
K1
=
2a
a + b
K1 =
a
a1
K1.
よって
aI(a, b) =
a
a1
a1I(a1, b1) ∴ I(a, b) = I(a1, b1).
同様にして
K
a
= I(a, b) = I(a1, b1) = I(a2, b2) = · · · = I(a∞, b∞).

三角関数
テータ関数
Proof (Cont.)
I(a∞, b∞) =
1
M(a, b)
I(1, 1) であるから
K
a
= I(a∞, b∞) =
1
M(a, b)
I(1, 1)
=
1
aM(1, b/a)
∫ π/2
0
dφ
=
1
aM(1, k′)
π
2
∴ M(1, k′
) =
π
2K
Corollary.
M(1,
√
2) =
π
?

三角関数
テータ関数
De?nition.
v ∈ R, i =
√
?1 とする．
sn(iv, k) := i
sn(v, k′
)
cn(v, k′)
,
cn(iv, k) :=
1
cn(v, k′)
,
dn(iv, k) :=
dn(v, k′
)
cn(v, k′)
.
これは y0 ∈ R をとって
∫ iy0
0
dx
√
(1 ? x2)(1 ? k2x2)
を考えればよい．

三角関数
テータ関数
u, v ∈ R に対し sn(u + iv, k) 等を加法定理の式で定めれば
周期極（1 位）零点（1 位）
sn 4K, 2K′
i 2mK + (2n ? 1)K′
i 2mK + 2nK′
i
cn 4K, 2K + 2K′
i 〃 (2m ? 1)K + 2nK′
i
dn 2K, 4K′
i 〃 (2m ? 1)K + (2n ? 1)K′
i
ただし K′
:= K(k′
), m, n ∈ Z である．

三角関数
テータ関数
テータ関数
簡単のため次の記法を用いる；
∏
:=
∞∏
n=1
,
∑
:=
∞∑
n=?∞
De?nition.
v ∈ C, τ ∈ H = {z ∈ C | Im z > 0}, z := eπiv
, q := eπiτ
とおく．
?1(v) := Cq1/4 z ? z?1
i
∏
(1 ? q2n
z2
)(1 ? q2n
z?2
)
?2(v) := Cq1/4
(z + z?1
)
∏
(1 + q2n
z2
)(1 + q2n
z?2
)
?3(v) := C
∏
(1 + q2n?1
z2
)(1 + q2n?1
z?2
)
?0(v) := C
∏
(1 ? q2n?1
z2
)(1 ? q2n?1
z?2
)
ここで C :=
∏
(1 ? q2n
) である．また ?3 := ?3(0) 等と書く．

三角関数
テータ関数
ここで
?0(v) = 0 ? q2n?1
z±2
= 1
? eπi
(
(2n?1)τ±2v
)
= 1
? (2n ? 1)τ ± 2v = 2m
? v = ±m ? (n ?
1
2
)τ

三角関数
テータ関数
零点 τ =
K′
K
i, v =
u
2K
のとき
?1 m + nτ 2mK + 2nK′
i
?2
(
m ? 1
2
)
+ nτ (2m ? 1)K + 2nK′
i
?3
(
m ? 1
2
)
+
(
n ? 1
2
)
τ (2m ? 1)K + (2n ? 1)K′
i
?0 m +
(
n ? 1
2
)
τ 2mK + (2n ? 1)K′
i
?0 = 0
( u
2K
)
?
u
2K
= m +
(
n ?
1
2
)
K′
K
i
u = 2mK + (2n ? 1) K′
i

三角関数
テータ関数
Proposition.
sn u = C1
?1(v)
?0(v)
,
cn u = C2
?2(v)
?0(v)
,
dn u = C3
?3(v)
?0(v)
.
Proposition.
?k(v + 2) = ?k(v) (k = 1, 2, 3, 0)
Proof.
v → v + 2 のとき， eπi(v+2)
= eπiv
より z → z から分かる．

三角関数
テータ関数
Proposition. (?k の Fourier 展開)
?1(v) = i
∑
(?1)n
q(2n?1
2 )
2
z2n?1
?2(v) =
∑
q(2n?1
2 )
2
z2n?1
?3(v) =
∑
qn2
z2n
?0(v) =
∑
(?1)n
qn2
z2n
Proposition. (熱方程式)
?2
?k
?v2
= 4πi
??k
?τ
Proof.
項別微分すればよい．

三角関数
テータ関数
Fact.
?(u) ? ?(v) = ??′2
1
?1(u + v)?1(u ? v)
?1(u)2?1(v)2
.
ただし ? の周期は 1, τ である．
Proposition.
?4
3 = 4q
d
dq
log
?2
?0
.

三角関数
テータ関数
Theorem.
n ∈ N, Φ(n) := #{(n1, n2, n3, n4) ∈ Z4
| n2
1 + n2
2 + n2
3 + n2
4 = n} とす
る．このとき
σ1(n) :=
∑
k∈N
k|n
k,
σ2(n) :=
∑
k∈4N
k|n
k,
σ(n) := σ1(n) ? σ2(n)
とすれば
Φ(n) = 8σ(n).

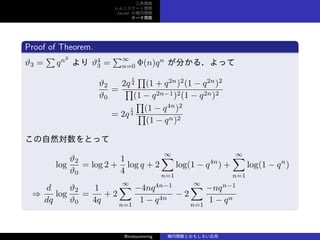
三角関数
テータ関数
Proof of Theorem.
?3 =
∑
qn2
より ?4
3 =
∑∞
n=0 Φ(n)qn
が分かる．よって
?2
?0
=
2q
1
4
∏
(1 + q2n
)2
(1 ? q2n
)2
∏
(1 ? q2n?1)2(1 ? q2n)2
= 2q
1
4
∏
(1 ? q4n
)2
∏
(1 ? qn)2
この自然対数をとって
log
?2
?0
= log 2 +
1
4
log q + 2
∞∑
n=1
log(1 ? q4n
) +
∞∑
n=1
log(1 ? qn
)
?
d
dq
log
?2
?0
=
1
4q
+ 2
∞∑
n=1
?4nq4n?1
1 ? q4n
? 2
∞∑
n=1
?nqn?1
1 ? qn

三角関数
テータ関数
Proof (Cont.)
?4
3 = 1 ? 8
∞∑
n=1
4nq4n
1 ? q4n
+ 8
∞∑
n=1
nqn
1 ? qn
= 1 ? 8
∞∑
n=1
4nq4n
∞∑
m=0
q4nm
+ 8
∞∑
n=1
nqn
∞∑
m=0
qnm
= 1 ? 8
∞∑
m=0
∞∑
n=1
4nq4n(m+1)
+ 8
∞∑
m=0
∞∑
n=1
nqn(m+1)
= 1 ? 8
∞∑
n=1
σ2(n)qn
+ 8
∞∑
n=1
σ1(n)qn
= 1 + 8
∞∑
n=1
σ(n)qn
以上より Φ(n) = 8σ(n).

狠狠撸

20150922冲楕円関数とおもしろい応用

More Related Content

20150922冲楕円関数とおもしろい応用