Multilayer neural networks
- 1. 1 вҖ«ШҘШ№ШҜШ§ШҜвҖ¬:вҖ«ШҜвҖ¬.вҖ«ШөШ§Щ„ШӯвҖ¬ вҖ«Ш§Щ„Ш№Ш§ШЁШҜЩҠЩҶвҖ¬ вҖ«ЩҠЩҶвҖ¬вҖ«ШІвҖ¬ вҖ«Ш¬Ш№ЩҒШұвҖ¬ вҖ«Ш§Щ…Щ„Ш№Щ„ЩҲЩ…Ш§ШӘвҖ¬ вҖ«ЩҲШӘЩӮШ§ЩҶШ©вҖ¬ вҖ«Ш§Щ„ШӯШ§ШіЩҲШЁвҖ¬ вҖ«Ш№Щ„ЩҲЩ…вҖ¬ вҖ«ЩғЩ„ЩҠШ©вҖ¬ вҖ«Ш§Щ„ЩҶЩҠЩ„ЩҠЩҶвҖ¬ вҖ«Ш¬Ш§Щ…Ш№Ш©вҖ¬ Dr gafar zen alabdeen salh (2011)
- 3. 3Dr gafar zen alabdeen salh (2011)
- 5. 5Dr gafar zen alabdeen salh (2011)
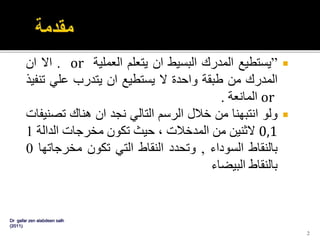
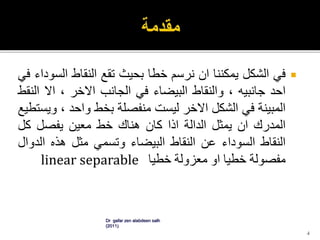
- 9. пӮЎвҖ«Ш§Щ„Щ…ШҜШұЩғвҖ¬вҖ«Щ…ШӘШ№ШҜШҜвҖ¬вҖ«Ш§Щ„Ш·ШЁЩӮШ§ШӘвҖ¬вҖ«ЩҮЩҲвҖ¬вҖ«ШҙШЁЩғШ©вҖ¬вҖ«Ш№ШөШЁЩҠШ©вҖ¬вҖ«ШЈЩ…Ш§Щ…ЩҠШ©вҖ¬вҖ«Ш§Щ„ШӘШәШ°ЩҠвҖ¬вҖ«Ш©вҖ¬вҖ«ШЁЩҮШ§вҖ¬ вҖ«Ш·ШЁЩӮШ©вҖ¬вҖ«ЩҲШ§ШӯШҜШ©вҖ¬ШҢвҖ«ШЈЩҲвҖ¬вҖ«ШЈЩғШ«ШұвҖ¬вҖ«Щ…Ш®ШЁШЈШ©вҖ¬.вҖ«ЩҲШӘЩӮЩ„ЩҠШҜЩҠШ§вҖ¬ШҢвҖ«ШӘШӘЩғЩҲЩҶвҖ¬вҖ«Ш§Щ„ШҙШЁвҖ¬вҖ«ЩғШ©вҖ¬вҖ«Щ…ЩҶвҖ¬ вҖ«Ш·ШЁЩӮШ©вҖ¬вҖ«Щ…ШҜШ®Ш§Щ„ШӘвҖ¬Input layerвҖ«Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«Ш§Щ„Щ…ШөШҜШұвҖ¬ШҢвҖ«ЩҲШ·ШЁЩӮШ©вҖ¬ вҖ«Щ…Ш®ШЁШЈШ©вҖ¬hidden layerвҖ«ШЈЩҲвҖ¬вҖ«Ш·ШЁЩӮШ©вҖ¬вҖ«Щ…ШӘЩҲШіШ·Ш©вҖ¬вҖ«ЩҲШ§ШӯШҜШ©вҖ¬вҖ«Ш№Щ„ЩҠвҖ¬вҖ«Ш§ШЈЩ„ЩӮЩ„вҖ¬ вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«Ш§Щ„ШӯШіШ§ШЁЩҠШ©вҖ¬ШҢвҖ«ЩҲШ·ШЁЩӮШ©вҖ¬вҖ«Щ…Ш®ШұШ¬Ш§ШӘвҖ¬output layer вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«Ш§Щ„ШӯШіШ§ШЁЩҠШ©вҖ¬.вҖ«ШӘЩҶШӘШҙШұвҖ¬вҖ«ШҘШҙШ§ШұШ§ШӘвҖ¬вҖ«Ш§Щ„Щ…ШҜШ®Ш§Щ„ШӘвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш§Ш§Щ„ШӘШ¬Ш§ЩҮвҖ¬ вҖ«Ш§ШЈЩ„Щ…Ш§Щ…ЩҠвҖ¬вҖ«Ш№Щ„ЩҠвҖ¬вҖ«ШЈШіШ§ШівҖ¬вҖ«Щ…ЩҶвҖ¬вҖ«Ш·ШЁЩӮШ©вҖ¬вҖ«Щ„Ш·ШЁЩӮШ©вҖ¬.вҖ«ЩҲШ§Щ„ШҙЩғЩ„вҖ¬вҖ«ЩҠЩҲШ¶ШӯвҖ¬вҖ«Щ…ШҜШұвҖ¬вҖ«ЩғвҖ¬ вҖ«ШЁШ·ШЁЩӮШӘЩҠЩҶвҖ¬вҖ«Щ…Ш®ШЁШЈШӘЩҠЩҶвҖ¬ 9Dr gafar zen alabdeen salh (2011)
- 10. 10Dr gafar zen alabdeen salh (2011)
- 14. пӮЎвҖ«ЩҠШӘШ§ШӯвҖ¬вҖ«ШӯШ§Щ„ЩҠШ§вҖ¬вҖ«ШЈЩғШ«ШұвҖ¬вҖ«Щ…ЩҶвҖ¬вҖ«Щ…Ш§ШҰШ©вҖ¬вҖ«Ш®ЩҲШ§ШұШІЩ…вҖ¬вҖ«ШӘШ№Щ„Щ…вҖ¬вҖ«Щ…Ш®ШӘЩ„ЩҒШ©вҖ¬ШҢвҖ«ШҘШ§Щ„вҖ¬вҖ«ШЈЩҶвҖ¬вҖ«Ш§Щ„Ш·ШұвҖ¬вҖ«ЩҠЩӮШ©вҖ¬ вҖ«Ш§ШЈЩ„ЩғШ«ШұвҖ¬вҖ«ШҙЩҠЩҲШ№Ш§вҖ¬вҖ«ЩҮЩҠвҖ¬вҖ«Ш§Ш§Щ„ЩҶШӘШҙШ§ШұвҖ¬вҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬.вҖ«ЩӮШҜвҖ¬вҖ«ЩғШ§ЩҶвҖ¬вҖ«ШЈЩҲЩ„вҖ¬вҖ«Ш§ЩӮШӘШұШ§ШӯвҖ¬вҖ«ЩҮШ°ЩҮвҖ¬ вҖ«Ш§Щ„Ш·ШұЩҠЩӮШ©вҖ¬вҖ«ШЁШұЩҠШіЩҲЩҶвҖ¬вҖ«ЩҲЩҮЩҲвҖ¬(Brson and ho 1969)вҖ«ШҘШ§Щ„вҖ¬вҖ«ШЈЩҶЩҮШ§вҖ¬ вҖ«ШЈЩҮЩ…Щ„ШӘвҖ¬вҖ«ШЁШіШЁШЁвҖ¬вҖ«Щ…ШӘШ·Щ„ШЁШ§ШӘЩҮШ§вҖ¬вҖ«Ш§Щ„ЩғШЁЩҠШұШ©вҖ¬вҖ«Щ„Щ„ШӯШіШ§ШЁШ§ШӘвҖ¬.вҖ«ЩҲЩҒЩҠвҖ¬вҖ«Щ…ЩҶШӘШөвҖ¬вҖ«ЩҒвҖ¬ вҖ«Ш§Щ„Ш«Щ…Ш§ЩҶЩҠЩҶЩҠШ§ШӘвҖ¬вҖ«Щ…ЩҶвҖ¬вҖ«Ш§Щ„ЩӮШұЩҶвҖ¬вҖ«Ш§Щ„Ш№ШҙШұЩҠЩҶвҖ¬вҖ«ЩҒЩӮШ·вҖ¬вҖ«Ш§Ш№ЩҠШҜвҖ¬вҖ«Ш§ЩғШӘШҙШ§ЩҒвҖ¬вҖ«Ш®ЩҲШ§ШұШІвҖ¬вҖ«Щ…вҖ¬вҖ«ШӘШ№Щ„Щ…вҖ¬ вҖ«Ш§Ш§Щ„ЩҶШӘШҙШ§ШұвҖ¬вҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬. пӮЎвҖ«ЩҠШіШӘЩ…ШұвҖ¬вҖ«Ш§Щ„ШӘШ№Щ„Щ…вҖ¬вҖ«ШЁЩҶЩҒШівҖ¬вҖ«Ш·ШұЩҠЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…ШҜШұЩғвҖ¬.вҖ«ШЁШӯЩҠШ«вҖ¬вҖ«ЩҠШӘЩ…вҖ¬вҖ«Ш¶ШЁШ·вҖ¬вҖ«Ш§вҖ¬вҖ«ШЈЩ„ЩҲШІШ§ЩҶвҖ¬. вҖ«ШЁЩҶШ§ШЎвҖ¬вҖ«Ш№Щ„ЩҠвҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬.вҖ«ЩҲЩ„ЩғЩҶвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„Щ…ШҜШұЩғвҖ¬вҖ«ЩғШ§ЩҶвҖ¬вҖ«ЩҮЩҶШ§ЩғвҖ¬вҖ«ЩҲШІЩҶвҖ¬вҖ«ЩҲШ§ШӯШҜвҖ¬вҖ«ЩҒЩӮШ·вҖ¬вҖ«Щ„вҖ¬вҖ«ЩғЩ„вҖ¬ вҖ«Щ…ШҜШ®Щ„вҖ¬ШҢвҖ«ЩҲЩ„ЩғЩ„вҖ¬вҖ«Щ…Ш®ШұШ¬вҖ¬вҖ«Щ…ЩҶвҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬.вҖ«ШЈЩ…Ш§вҖ¬вҖ«ЩҮЩҶШ§вҖ¬вҖ«ЩҒЩҠЩҲШ¬ШҜвҖ¬вҖ«Ш§Щ„ЩғШ«ЩҠШұвҖ¬вҖ«Щ…ЩҶвҖ¬ вҖ«Ш§ШЈЩ„ЩҲШІШ§ЩҶвҖ¬ШҢвҖ«ЩҲЩҠШіШ§ЩҮЩ…вҖ¬вҖ«ЩғЩ„вҖ¬вҖ«ЩҲШІЩҶвҖ¬вҖ«Щ…ЩҶЩҮШ§вҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«ШЈЩғШ«ШұвҖ¬вҖ«Щ…ЩҶвҖ¬вҖ«Щ…Ш®ШұШ¬вҖ¬вҖ«ЩҲШ§ШӯШҜвҖ¬. 14Dr gafar zen alabdeen salh (2011)
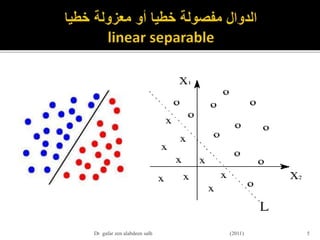
- 18. пӮЎвҖ«ЩҲШӘШ¬ШҜЩҠШҜвҖ¬вҖ«Ш§Щ„ЩҲШІЩҶвҖ¬вҖ«ЩҠЩғЩҲЩҶвҖ¬вҖ«Ш№Щ„ЩҠвҖ¬вҖ«Ш§Щ„ЩҶШӯЩҲвҖ¬вҖ«Ш§Щ„ШӘШ§Щ„ЩҠвҖ¬: пӮЎWjk (p+1)= wjk(p) +вҲҶWjk (p) пӮЎвҲҶWjk (p)= ОұГ—yj(p) Г—Оҙk(p) пӮЎвҖ«ШӯЩҠШ«вҖ¬Оҙk(p)вҖ«Ш§Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Ш№ЩҶШҜвҖ¬ вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬ вҖ«ШЈЩҲвҖ¬ вҖ«Щ…ЩҠЩ„вҖ¬kвҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«ЩҒЩҠвҖ¬ вҖ«Ш§Щ„ШӘЩғШұШ§ШұвҖ¬ вҖ«Ш№ЩҶШҜвҖ¬ вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬p пӮЎвҖ«Ш§Щ„Щ…ЩҠЩ„вҖ¬ вҖ«ЩҮЩҲвҖ¬ вҖ«Щ…Ш§вҖ¬: пӮЎвҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬ вҖ«ЩҠШӘШӯШҜШҜвҖ¬вҖ«Ш§ЩҲвҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«Щ…ЩҠЩ„вҖ¬вҖ«ШЁШ§ЩҶЩҮвҖ¬вҖ«ШҜШ§Щ„Ш©вҖ¬ вҖ«Щ…ШҙШӘЩӮШ©вҖ¬вҖ«Ш§ШівҖ¬вҖ«Ш§Щ„ШӘЩҶШҙЩҠШ·вҖ¬f вҖ«Ш§Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ вҖ«Ш№ЩҶШҜвҖ¬ вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«ЩҒЩҠвҖ¬ вҖ«Щ…Ш¶ШұЩҲШЁШ©вҖ¬.вҖ«Ш№вҖ¬ вҖ«ЩҶШӯШөЩ„вҖ¬ вҖ«Щ„Ш°Щ„ЩғвҖ¬вҖ«Щ„ЩҠвҖ¬ вҖ«Щ…Ш§ЩҠЩ„ЩҠвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬kвҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ вҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«ЩҒЩҠвҖ¬: пӮЎ Оҙk(p)= F '[XK(P)] Г— ek(p) пӮЎвҖ«ШӯЩҠШ«вҖ¬XK(P)вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Ш§Щ„Щ…ЩҲШІЩҲЩҶШ©вҖ¬ вҖ«Ш§Щ„Щ…ШҜШ®Ш§Щ„ШӘвҖ¬ вҖ«ШөШ§ЩҒЩҠвҖ¬kвҖ«Ш§Щ„ШӘЩғШұШ§ШұвҖ¬ вҖ«ЩҒЩҠвҖ¬ p 18Dr gafar zen alabdeen salh (2011)
- 19. 19Dr gafar zen alabdeen salh (2011)
- 20. пӮЎвҖ«ШӯЩҠШ«вҖ¬mвҖ«Ш№ШҜШҜвҖ¬вҖ«Ш§Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬вҖ«Щ„Ш°Щ„ЩғвҖ¬вҖ«ЩҠЩ…ЩғвҖ¬вҖ«ЩҶвҖ¬вҖ«ЩғШӘШ§ШЁШ©вҖ¬ вҖ«Ш§Щ„Щ…Ш№Ш§Щ„Ш©вҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬вҖ«Ш№Щ„ЩҠвҖ¬вҖ«Ш§Щ„ЩҶШӯЩҲвҖ¬вҖ«Ш§Щ„ШӘШ§Щ„ЩҠвҖ¬:Оҙk(p)= yk(p)Г—[1- yk(p)] Г— ek(p) 20 k m i pikwpikxp k X пҒұпҖӯпғҘ пҖҪ пӮҙпҖҪ 1 )()()( )( 1 1 )( pkx e p k y пҖӯ пҖ« пҖҪ Dr gafar zen alabdeen salh (2011)
- 21. пӮЎвҖ«ЩҠЩ…ЩғЩҶЩҶШ§вҖ¬ вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬ вҖ«Щ„Щ„Ш·ШЁЩӮШ©вҖ¬ вҖ«Ш§Щ„ЩҲШІЩҶвҖ¬ вҖ«ШӘШөШӯЩҠШӯвҖ¬ вҖ«Щ„ШӯШіШ§ШЁвҖ¬вҖ«ШӘШ·ШЁЩҠвҖ¬вҖ«ЩӮШ©вҖ¬вҖ«ЩҶЩҒШівҖ¬ вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ вҖ«Щ„Ш·ШЁЩӮШ©вҖ¬ вҖ«Ш§Щ„Щ…Ш№Ш§ШҜЩ„Ш©вҖ¬: пӮЎWij (p+1)= Wij (p) +вҲҶ Wij (p) пӮЎвҲҶ Wij (p) = ОұГ—Xi(p) Г—Оҙj(p) пӮЎвҖ«ШӯЩҠШ«вҖ¬вҖ«ШӘЩ…Ш«Щ„вҖ¬Оҙj(p)вҖ«Щ…ЩҠЩ„вҖ¬вҖ«Ш§ЩҲвҖ¬вҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬вҖ«Ш№ЩҶШҜвҖ¬вҖ«Ш§Щ„Ш№ШөШЁЩҲЩҶвҖ¬jвҖ«ЩҒЩҠвҖ¬ вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬: пӮЎвҖ«ШӯЩҠШ«вҖ¬IвҖ«Ш№ШҜШҜвҖ¬вҖ«Ш§Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ 21 пғҘпҖҪ пӮҙпҖӯпӮҙпҖҪ I k jkkjjj pwppypyp 1 )()()](1[)()( пҒӨпҒӨ Dr gafar zen alabdeen salh (2011)
- 22. пӮЎnвҖ«Ш§Щ„Щ…ШҜШ®Ш§Щ„ШӘвҖ¬ вҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«ЩҒЩҠвҖ¬ вҖ«Ш§Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬ вҖ«Ш№ШҜШҜвҖ¬ пӮЎвҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬ вҖ«Ш§Ш§Щ„ЩҶШӘШҙШ§ШұвҖ¬ вҖ«ШӘШҜШұЩҠШЁвҖ¬ вҖ«Ш®ЩҲШ§ШұШІЩ…ЩҠШ©вҖ¬ вҖ«ШЈШ§Щ„ЩҶвҖ¬ вҖ«ЩҲЩҶШіШӘШ®Щ„ШөвҖ¬ 22 )( 1 1 )( pjx e p j y пҖӯ пҖ« пҖҪ j n i pijwpixp j X пҒұпҖӯпғҘ пҖҪ пӮҙпҖҪ 1 )()()( Dr gafar zen alabdeen salh (2011)
- 23. пӮЎвҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬вҖ«Ш§Ш§Щ„ЩҲЩ„ЩҠвҖ¬:вҖ«ЩҲШ¶Ш№вҖ¬вҖ«Ш§Щ„ЩӮЩҠЩ…вҖ¬вҖ«Ш§Ш§Щ„ШЁШӘШҜШ§ШҰЩҠШ©вҖ¬ вҖ«ШӘШӯШҜЩҠШҜвҖ¬вҖ«Ш§ШЈЩ„ЩҲШІШ§ЩҶвҖ¬ШҢвҖ«Ш§Ш§Щ„ШЁШӘШҜШ§ШҰЩҠШ©вҖ¬вҖ«ШЁШӘЩҲШІЩҠШ№вҖ¬вҖ«Щ…ЩҶШӘШёЩ…вҖ¬вҖ«Щ„ШЈЩ„ШұЩӮШ§Щ…вҖ¬вҖ«Ш§Щ„Ш№ШҙЩҲШ§ШҰЩҠШ©вҖ¬вҖ«ШҜШ§Ш®Щ„вҖ¬вҖ«Щ…ШҜЩҠвҖ¬вҖ«ШөШәЩҠвҖ¬вҖ«ШұвҖ¬вҖ«ШЈЩҠвҖ¬вҖ«ШӘЩӮШ№вҖ¬вҖ«ЩҒЩҠвҖ¬ вҖ«Ш§Щ„Щ…ШҜЩүвҖ¬[-2.4/Fi, 2.4/Fi] вҖ«ШӯЩҠШ«вҖ¬FiвҖ«ШҘШ¬Щ…Ш§Щ„ЩҠвҖ¬вҖ«Ш№ШҜШҜвҖ¬вҖ«Ш§Щ„Щ…ШҜШ®Ш§Щ„ШӘвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬iвҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„ШҙШЁЩғШ©вҖ¬.вҖ«ЩҲЩҠШӯШҜШ«вҖ¬вҖ«ШӘШӯШҜЩҠШҜвҖ¬вҖ«Ш§Щ„ЩӮЩҠЩ…вҖ¬вҖ«Ш§Ш§Щ„ШЁШӘШҜШ§ШҰвҖ¬вҖ«ЩҠШ©вҖ¬ вҖ«Щ„ШЈЩ„ЩҲШІШ§ЩҶвҖ¬вҖ«Ш№Щ„ЩҠвҖ¬вҖ«ШЈШіШ§ШівҖ¬вҖ«Ш№ШөШЁЩҲЩҶвҖ¬вҖ«ШЁШ№ШҜвҖ¬вҖ«Ш№ШөШЁЩҲЩҶвҖ¬. пӮЎвҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬вҖ«Ш§Щ„Ш«Ш§ЩҶЩҠШ©вҖ¬:вҖ«Ш§Щ„ШӘЩҶШҙЩҠШ·вҖ¬ пӮЎвҖ«ШӘЩҶШҙЩҠШ·вҖ¬вҖ«Ш§Ш§Щ„ЩҶШӘШҙШ§ШұвҖ¬вҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬вҖ«Щ„Щ„ШҙШЁЩғШ©вҖ¬вҖ«Ш§Щ„Ш№ШөШЁЩҠШ©вҖ¬вҖ«Ш№ЩҶвҖ¬вҖ«Ш·ШұЩҠЩӮвҖ¬вҖ«ШӘШ·ШЁЩҠЩӮвҖ¬вҖ«Ш§Щ„Щ…ШҜШ®Ш§Щ„ШӘвҖ¬ x1(p),x2(p),вҖҰxn(p)ШҢ пӮЎвҖ«ЩҲШ§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Ш§Щ„Щ…ШұШәЩҲШЁвҖ¬вҖ«ЩҒЩҠЩҮШ§вҖ¬Yd,1(p) , Yd,2(p) ,вҖҰ.,Yd,n(p) пҒұвҖ«ЩҲШӯШіШ§ШЁвҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Ш§Щ„ЩҒШ№Щ„ЩҠШ©вҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬: пӮЎвҖ«ШӯЩҠШ«вҖ¬nвҖ«Щ…ШҜШ®Ш§Щ„ШӘвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬jвҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬ШҢвҖ«ЩҲвҖ¬sigmoidвҖ«ШҜШ§Щ„Ш©вҖ¬вҖ«ШӘЩҶШҙЩҠШ·вҖ¬вҖ«Ш§Ш§Щ„ШівҖ¬ 23 пғә пғә пғ» пғ№ пғӘ пғӘ пғ« пғ© пғҘ пҖҪ пҖӯпҖҪ n i jpijwpixsigmoidp j y 1 )()()( пҒұ Dr gafar zen alabdeen salh (2011)
- 25. пӮЎвҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬вҖ«Ш§Щ„Ш«Ш§Щ„Ш«Ш©вҖ¬:вҖ«ШӘШҜШұЩҠШЁвҖ¬вҖ«Ш§ШЈЩ„ЩҲШІШ§ЩҶвҖ¬:вҖ«ШӘШ¬ШҜЩҠШҜвҖ¬вҖ«ШЈЩҲШІШ§ЩҶвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«ШҙШЁЩғШ©вҖ¬вҖ«Ш§Ш§Щ„ЩҶШӘШҙШ§ШұвҖ¬вҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬вҖ«Ш№ЩҶвҖ¬вҖ«Ш·ШұЩҠЩӮвҖ¬вҖ«ЩҶШҙШұвҖ¬вҖ«Ш§ШЈЩ„Ш®Ш·Ш§ШЎвҖ¬вҖ«Ш§Щ„Щ…ШөвҖ¬вҖ«Ш§ШӯШЁШ©вҖ¬ вҖ«Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬ пғҳвҖ«ШӯШіШ§ШЁвҖ¬вҖ«Щ…ЩҠЩ„вҖ¬вҖ«Ш§ЩҲвҖ¬вҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ пғҳОҙk(p)= yk(p)Г—[1-yk(p)] Г— ek(p) пғҳвҖ«ШӯЩҠШ«вҖ¬: пғҳek(p) = Ydk(p) вҖ“Yk(p) where p=1,2,3,вҖҰ пғҳвҖ«ЩҲШӯШіШ§ШЁвҖ¬вҖ«ШӘШөШӯЩҠШӯвҖ¬вҖ«Ш§Ш§Щ„ЩҲШІШ§ЩҶвҖ¬: пӮЎWjk (p+1)= wjk(p) +вҲҶWjk (p) пӮЎвҲҶWjk (p)= ОұГ—yj(p) Г—Оҙk(p) пғҳвҖ«ЩҲШӘШ¬ШҜЩҠШҜвҖ¬вҖ«Ш§Ш§Щ„ЩҲШІШ§ЩҶвҖ¬вҖ«Ш№ЩҶШҜвҖ¬вҖ«Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬: пғҳWjk (p+1)= wjk(p) + ОұГ—yj(p) Г—Оҙk(p) пғҳвҖ«ШӯШіШ§ШЁвҖ¬вҖ«Щ…ЩҠЩ„вҖ¬вҖ«Ш§ЩҲвҖ¬вҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬: пғҳ пӮЎWij (p+1)= Wij (p) +вҲҶ Wij (p) пӮЎвҲҶ Wij (p) = ОұГ—Xi(p) Г—Оҙj(p) пӮЎвҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬вҖ«Ш§Щ„ШұШ§ШЁШ№Ш©вҖ¬:вҖ«Ш§Щ„ШӘЩғШұШ§ШұвҖ¬ пӮЎвҖ«ШІЩҠШ§ШҜШ©вҖ¬вҖ«Ш§Щ„ШӘЩғШұШ§ШұвҖ¬pвҖ«ШЁЩ…ЩӮШҜШ§ШұвҖ¬вҖ«ЩҲШ§ШӯШҜвҖ¬вҖ«ШөШӯЩҠШӯвҖ¬ШҢвҖ«ЩҲШ§Щ„Ш№ЩҲШҜШ©вҖ¬вҖ«Ш§Щ„ЩҠвҖ¬вҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬вҖ«Ш§Щ„Ш«Ш§ЩҶЩҠШ©вҖ¬ШҢвҖ«ЩҲШӘЩғШұШ§ШұвҖ¬вҖ«Ш§Щ„Ш№Щ…Щ„ЩҠШ©вҖ¬вҖ«ШӯШӘЩҠвҖ¬вҖ«ЩҠШӘШӯЩӮЩӮвҖ¬вҖ«Щ…Ш№вҖ¬вҖ«ЩҠШ§ШұвҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«Ш§Щ„Щ…Ш®ШӘШ§ШұвҖ¬ 25 Dr gafar zen alabdeen salh (2011) пғҘпҖҪ пӮҙпҖӯпӮҙпҖҪ I k jkkjjj pwppypyp 1 )()()](1[)()( пҒӨпҒӨ
- 27. пӮЎвҖ«ЩҲЩҠЩғЩҲЩҶвҖ¬вҖ«ШӘШ§Ш«ЩҠШұвҖ¬вҖ«ШӘШ·ШЁЩҠЩӮвҖ¬вҖ«Ш§Щ„Ш№ШӘШЁЩҮвҖ¬вҖ«Ш№Щ„ЩҠвҖ¬вҖ«Ш§Щ„Ш№ШөШЁЩҲЩҶвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„Ш·вҖ¬вҖ«ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬ШҢ вҖ«Ш§ЩҲвҖ¬вҖ«Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Щ…Щ…Ш«Ш§Щ„вҖ¬вҖңвҖ«ШЁЩҲШІЩҶЩҮвҖ¬ОёШҢвҖ«Щ…ШӘШөШ§Щ„вҖ¬вҖ«ШЁЩ…ШҜШ®Ш§Щ„ШӘвҖ¬вҖ«Ш«Ш§ШЁШӘЩҮвҖ¬ вҖ«ШӘШіШ§ЩҲЩҠвҖ¬1-. пӮЎвҖ«ЩҲШӘШӯШҜШҜвҖ¬вҖ«Ш§ШЈЩ„ЩҲШІШ§ЩҶвҖ¬вҖ«Ш§Ш§Щ„ШЁШӘШҜШ§ШҰЩҠШ©вҖ¬ШҢвҖ«ЩҲЩ…ШіШӘЩҲЩҠШ§ШӘвҖ¬вҖ«Ш§Щ„Ш№ШӘШЁШ©вҖ¬вҖ«Ш№ШҙЩҲШ§ШҰЩҠвҖ¬вҖ«Ш§вҖ¬вҖ«ЩғЩ…Ш§вҖ¬вҖ«ЩҠЩ„ЩҠвҖ¬ : пӮЎW13=0.5 , W14=0.9 , W23=0.4 , W24=1.0 , W45=1.1 , Оё3=0.8 , Оё4=-0.1 AND Оё5=0.3 27Dr gafar zen alabdeen salh (2011)
- 28. пӮЎвҖ«Щ„ЩҶШӘЩҶШ§ЩҲЩ„вҖ¬вҖ«ЩҒШҰШ©вҖ¬вҖ«ШӘШҜШұЩҠШЁвҖ¬вҖ«ШӯЩҠШ«вҖ¬X1,X2вҖ«ЩҠШіШ§ЩҲЩҠШ§вҖ¬1ШҢвҖ«ЩҲШ§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Ш§Щ„Щ…ШұШәЩҲШЁвҖ¬ вҖ«ЩҒЩҠЩҮШ§вҖ¬Yd,5вҖ«ШӘШіШ§ЩҲЩҠвҖ¬0вҖ«ЩҲШӘШӯШіШЁвҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Ш§Щ„ЩҒШ№Щ„ЩҠШ©вҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬3вҖ«ЩҲвҖ¬4вҖ«ЩҒЩҠвҖ¬ вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬вҖ«ЩғЩ…Ш§вҖ¬вҖ«ЩҠЩ„ЩҠвҖ¬: пӮЎ Y3=sigmoid(x1*w13+x2*w23-Оё3) пӮЎ 1/[1+e-(1*0.5+1*0.4-1*0.8)]=0.5250 пӮЎ Y4=sigmoid(x1*w14+x2*w24-Оё4) пӮЎ 1/[1+e-(1*0.9+1*1.0+1*0.1)]=0.8808 пӮЎвҖ«ЩҲШ§Ш§Щ„ЩҶвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Ш§Щ„ЩҒШ№Щ„ЩҠШ©вҖ¬ вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ вҖ«ШӘШӘШӯШҜШҜвҖ¬5вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ вҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«ЩҒЩҠвҖ¬: пӮЎ Y5=sigmoid(y3*w35+y4*w45-Оё5) пӮЎ 1/[1+e-(-0.5250*1.2+0.8808*1.1-1*0.3)]=0.5097 28Dr gafar zen alabdeen salh (2011)
- 29. пӮЎ e= yd,5 вҖ“y5 =0-0.5097=-0.5097 пӮЎвҖ«ШӘШҜШұЩҠШЁвҖ¬ вҖ«Ш§Щ„ШӘШ§Щ„ЩҠШ©вҖ¬ вҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬ вҖ«ЩҲШӘЩғЩҲЩҶвҖ¬вҖ«Ш§Ш§Щ„ЩҲШІШ§ЩҶвҖ¬.вҖ«Щ„ШӘШ¬ШҜЩҠШҜвҖ¬вҖ«Ш§Ш§Щ„ЩҲШІШ§ЩҶвҖ¬ШҢ вҖ«ШҙШЁЩғШӘЩҶШ§вҖ¬ вҖ«ЩҒЩҠвҖ¬ вҖ«Ш§Щ„Ш№ШӘШЁШ©вҖ¬ вҖ«ЩҲЩ…ШіШӘЩҲЩҠШ§ШӘвҖ¬вҖ«ЩҒШ§ЩҶЩҶШ§вҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«ЩҶЩҶШҙШұвҖ¬eвҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«Щ…ЩҶвҖ¬ вҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬ вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Ш§Щ„ЩҠвҖ¬вҖ«Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…ШҜШ®Ш§Щ„ШӘвҖ¬. пӮЎвҖ«Ш§ЩҲШ§Щ„вҖ¬вҖңвҖ«Щ…ЩҠЩ„вҖ¬ вҖ«ЩҶШӯШіШЁвҖ¬ ШҢвҖ«Ш§ЩҲвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬5вҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«ЩҒЩҠвҖ¬ вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬: пӮЎ Оҙ5= y5Г—[1-y5] Г— e=0.5097*(1-0.5097)*(-0.5097)=-0.1274 пӮЎвҖ«ШЁШ§ЩҒШӘШұШ§Ш¶вҖ¬ вҖ«Ш§Щ„ЩҲШІЩҶвҖ¬ вҖ«ШӘШөШӯЩҠШӯШ§ШӘвҖ¬ вҖ«Ш°Щ„ЩғвҖ¬ вҖ«ШЁШ№ШҜвҖ¬ вҖ«ЩҶШӯШҜШҜвҖ¬ вҖ«Ш«Щ…вҖ¬вҖ«Ш§ЩҶвҖ¬вҖ«Щ…вҖ¬ вҖ«Щ…Ш№Щ„Щ…Ш©вҖ¬вҖ«Ш№ШҜЩ„вҖ¬ вҖ«Ш§Щ„ШӘШ№Щ„Щ…вҖ¬Оұ=0.1 29Dr gafar zen alabdeen salh (2011)
- 30. пӮЎвҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«Ш§ЩҶШӯШҜШ§ШұШ§ШӘвҖ¬ вҖ«ШЈЩҲвҖ¬ вҖ«Щ…ЩҠЩҲЩ„вҖ¬ вҖ«Ш°Щ„ЩғвҖ¬ вҖ«ШЁШ№ШҜвҖ¬ вҖ«ЩҶШӯШіШЁвҖ¬3,4вҖ«ЩҒЩҠвҖ¬ вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬ вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬: пӮЎ Оҙ3= y3Г—[1-y3] Г— Оҙ5Г—w35 =0.5250*(1-0.5250)*(-0.1274)*(- 1.2)=0.0381 пӮЎ Оҙ4= y4Г—[1-y4] Г— Оҙ5Г—w45 =0.8808*(1- 0.8808)*(-0.1274)*1.1=- 0.0147 пӮЎвҖ«Ш§ШЈЩ„ЩҲШІШ§ЩҶвҖ¬ вҖ«ШӘШөШӯЩҠШӯШ§ШӘвҖ¬ вҖ«Ш°Щ„ЩғвҖ¬ вҖ«ШЁШ№ШҜвҖ¬ вҖ«ЩҶШӯШҜШҜвҖ¬: 30Dr gafar zen alabdeen salh (2011)
- 31. пӮЎ вҲҶ W13= ОұГ—X1Г—Оҙ3 = 0.1Г—1Г—0.038=0.0038 пӮЎ вҲҶ W23= ОұГ—X2Г—Оҙ3 = 0.1Г—1Г—0.038=0.0038 пӮЎ вҲҶ Оё3= ОұГ—(-1)Г—Оҙ3 = 0.1Г—(-1) Г—0.038=-0.0038 пӮЎ вҲҶ W14= ОұГ—X1Г—Оҙ4 = 0.1Г—1Г—(-0.0147)=-0.0015 пӮЎ вҲҶ W24= ОұГ—X2Г—Оҙ4 =0.1Г—1Г—(-0.0147)=-0.0015 пӮЎ вҲҶ Оё4= ОұГ—(-1)Г—Оҙ4=0.1Г—(-1)Г—(-0.0147)=0.0015 31Dr gafar zen alabdeen salh (2011)
- 32. пӮЎвҖ«ЩҲШ§Ш®ЩҠШұШ§вҖ¬вҖңвҖ«ЩҶШ¬ШҜШҜвҖ¬вҖ«ЩғЩ„вҖ¬вҖ«Ш§Ш§Щ„ЩҲШІШ§ЩҶвҖ¬ШҢвҖ«ЩҲЩ…ШіШӘЩҲЩҠШ§ШӘвҖ¬вҖ«Ш§Щ„Ш№ШӘШЁЩҮвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«ШҙШЁЩғвҖ¬вҖ«ШӘЩҶШ§вҖ¬: пӮЎ W13= W13 +вҲҶ W13 = 0.5+0.0038=0.5038 пӮЎ W14= W14 +вҲҶ W14 = 0.9-0.0015=0.8985 пӮЎ W23= W23 +вҲҶ W23 = 0.4+0.0038=0.4038 пӮЎ W24= W24 +вҲҶ W24 = 1.0-0.0015=0.9985 пӮЎ W35= W35 +вҲҶ W35 = -1.2-0.0067=-0.2067 пӮЎ W45= W45 +вҲҶ W45 = 1.1-0.0112=1.0888 пӮЎ Оё3= Оё3 +вҲҶ Оё3 = 0.8-0.0038=0.7962 пӮЎ Оё4= Оё4 +вҲҶ Оё4 = -0.1+0.0015=-0.0985 пӮЎ Оё5= Оё5 +вҲҶ Оё5 = 0.3+0.0127=0.3127 32Dr gafar zen alabdeen salh (2011)
- 34. пӮЎвҖ«ШҙШЁЩғШӘЩҶШ§вҖ¬ вҖ«ШӘШҜШұЩҠШЁвҖ¬ вҖ«ЩҠШӯШӘШ§Ш¬вҖ¬вҖ«Ш§Щ„ЩҠвҖ¬224вҖ«ЩҒШӘШұШ©вҖ¬вҖ«Ш§ЩҲвҖ¬896вҖ«Щ„ШӘЩҶЩҒЩҠШ°ЩҮШ§вҖ¬ вҖ«ШӘЩғШұШ§ШұвҖ¬ вҖ«Ш№Щ…Щ„ЩҠШ©вҖ¬orвҖ«ЩҒШҰШ©вҖ¬ вҖ«ЩҲШӘШӯЩӮЩӮвҖ¬ вҖ«Ш§Щ„Щ…Ш§ЩҶШ№Ш©вҖ¬вҖ«Ш§Ш§Щ„ЩҲШІШ§ЩҶвҖ¬вҖ«Ш§Щ„Ш№ШӘШЁвҖ¬ вҖ«ЩҲЩ…ШіШӘЩҲЩҠШ§ШӘвҖ¬ ШҢвҖ«Ш©вҖ¬ вҖ«Щ…Ш№ЩҠШ§ШұвҖ¬ вҖ«Ш§Щ„ЩҶЩҮШ§ШҰЩҠШ©вҖ¬вҖ«Ш§Щ„Ш®Ш·Ш§вҖ¬вҖ«Ш§Щ„Щ…Ш®ШӘШ§ШұвҖ¬ 34Dr gafar zen alabdeen salh (2011)
- 35. пӮЎ вҖ«Ш§Щ„Ш°ЩғЩҠШ©вҖ¬ вҖ«Ш§Щ„ЩҶШёЩ…вҖ¬ вҖ«ШҜЩ„ЩҠЩ„вҖ¬ The End. пӮЎ Thank you for your patience! Dr gafar zen alabdeen salh (2011) 35



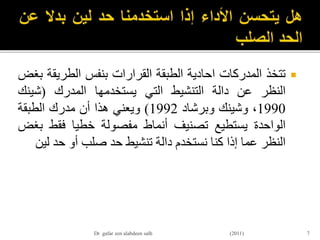




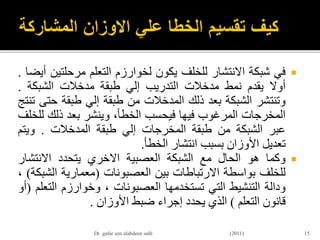


![пӮЎвҖ«ЩҲШӘШ¬ШҜЩҠШҜвҖ¬вҖ«Ш§Щ„ЩҲШІЩҶвҖ¬вҖ«ЩҠЩғЩҲЩҶвҖ¬вҖ«Ш№Щ„ЩҠвҖ¬вҖ«Ш§Щ„ЩҶШӯЩҲвҖ¬вҖ«Ш§Щ„ШӘШ§Щ„ЩҠвҖ¬:
пӮЎWjk (p+1)= wjk(p) +вҲҶWjk (p)
пӮЎвҲҶWjk (p)= ОұГ—yj(p) Г—Оҙk(p)
пӮЎвҖ«ШӯЩҠШ«вҖ¬Оҙk(p)вҖ«Ш§Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Ш№ЩҶШҜвҖ¬ вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬ вҖ«ШЈЩҲвҖ¬ вҖ«Щ…ЩҠЩ„вҖ¬kвҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«ЩҒЩҠвҖ¬
вҖ«Ш§Щ„ШӘЩғШұШ§ШұвҖ¬ вҖ«Ш№ЩҶШҜвҖ¬ вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬p
пӮЎвҖ«Ш§Щ„Щ…ЩҠЩ„вҖ¬ вҖ«ЩҮЩҲвҖ¬ вҖ«Щ…Ш§вҖ¬:
пӮЎвҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬ вҖ«ЩҠШӘШӯШҜШҜвҖ¬вҖ«Ш§ЩҲвҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«Щ…ЩҠЩ„вҖ¬вҖ«ШЁШ§ЩҶЩҮвҖ¬вҖ«ШҜШ§Щ„Ш©вҖ¬ вҖ«Щ…ШҙШӘЩӮШ©вҖ¬вҖ«Ш§ШівҖ¬вҖ«Ш§Щ„ШӘЩҶШҙЩҠШ·вҖ¬f
вҖ«Ш§Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ вҖ«Ш№ЩҶШҜвҖ¬ вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«ЩҒЩҠвҖ¬ вҖ«Щ…Ш¶ШұЩҲШЁШ©вҖ¬.вҖ«Ш№вҖ¬ вҖ«ЩҶШӯШөЩ„вҖ¬ вҖ«Щ„Ш°Щ„ЩғвҖ¬вҖ«Щ„ЩҠвҖ¬
вҖ«Щ…Ш§ЩҠЩ„ЩҠвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬kвҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ вҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«ЩҒЩҠвҖ¬:
пӮЎ Оҙk(p)= F '[XK(P)] Г— ek(p)
пӮЎвҖ«ШӯЩҠШ«вҖ¬XK(P)вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Ш§Щ„Щ…ЩҲШІЩҲЩҶШ©вҖ¬ вҖ«Ш§Щ„Щ…ШҜШ®Ш§Щ„ШӘвҖ¬ вҖ«ШөШ§ЩҒЩҠвҖ¬kвҖ«Ш§Щ„ШӘЩғШұШ§ШұвҖ¬ вҖ«ЩҒЩҠвҖ¬
p
18Dr gafar zen alabdeen salh (2011)](https://image.slidesharecdn.com/multilayerneuralnetworks-170808125250/85/Multilayer-neural-networks-18-320.jpg)
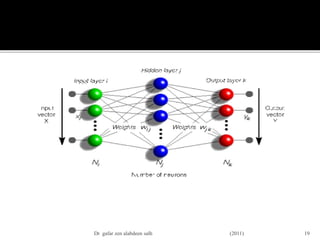
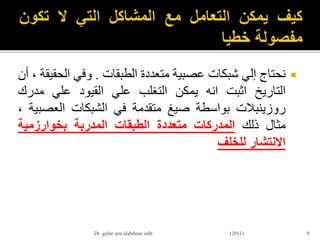
![пӮЎвҖ«ШӯЩҠШ«вҖ¬mвҖ«Ш№ШҜШҜвҖ¬вҖ«Ш§Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬вҖ«Щ„Ш°Щ„ЩғвҖ¬вҖ«ЩҠЩ…ЩғвҖ¬вҖ«ЩҶвҖ¬вҖ«ЩғШӘШ§ШЁШ©вҖ¬
вҖ«Ш§Щ„Щ…Ш№Ш§Щ„Ш©вҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬вҖ«Ш№Щ„ЩҠвҖ¬вҖ«Ш§Щ„ЩҶШӯЩҲвҖ¬вҖ«Ш§Щ„ШӘШ§Щ„ЩҠвҖ¬:Оҙk(p)= yk(p)Г—[1-
yk(p)] Г— ek(p)
20
k
m
i
pikwpikxp
k
X пҒұпҖӯпғҘ
пҖҪ
пӮҙпҖҪ
1
)()()(
)(
1
1
)(
pkx
e
p
k
y
пҖӯ
пҖ«
пҖҪ
Dr gafar zen alabdeen salh (2011)](https://image.slidesharecdn.com/multilayerneuralnetworks-170808125250/85/Multilayer-neural-networks-20-320.jpg)
()( пҒӨпҒӨ
Dr gafar zen alabdeen salh (2011)](https://image.slidesharecdn.com/multilayerneuralnetworks-170808125250/85/Multilayer-neural-networks-21-320.jpg)

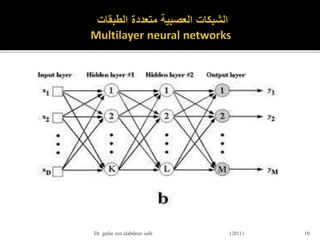
![пӮЎвҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬вҖ«Ш§Ш§Щ„ЩҲЩ„ЩҠвҖ¬:вҖ«ЩҲШ¶Ш№вҖ¬вҖ«Ш§Щ„ЩӮЩҠЩ…вҖ¬вҖ«Ш§Ш§Щ„ШЁШӘШҜШ§ШҰЩҠШ©вҖ¬
вҖ«ШӘШӯШҜЩҠШҜвҖ¬вҖ«Ш§ШЈЩ„ЩҲШІШ§ЩҶвҖ¬ШҢвҖ«Ш§Ш§Щ„ШЁШӘШҜШ§ШҰЩҠШ©вҖ¬вҖ«ШЁШӘЩҲШІЩҠШ№вҖ¬вҖ«Щ…ЩҶШӘШёЩ…вҖ¬вҖ«Щ„ШЈЩ„ШұЩӮШ§Щ…вҖ¬вҖ«Ш§Щ„Ш№ШҙЩҲШ§ШҰЩҠШ©вҖ¬вҖ«ШҜШ§Ш®Щ„вҖ¬вҖ«Щ…ШҜЩҠвҖ¬вҖ«ШөШәЩҠвҖ¬вҖ«ШұвҖ¬вҖ«ШЈЩҠвҖ¬вҖ«ШӘЩӮШ№вҖ¬вҖ«ЩҒЩҠвҖ¬
вҖ«Ш§Щ„Щ…ШҜЩүвҖ¬[-2.4/Fi, 2.4/Fi]
вҖ«ШӯЩҠШ«вҖ¬FiвҖ«ШҘШ¬Щ…Ш§Щ„ЩҠвҖ¬вҖ«Ш№ШҜШҜвҖ¬вҖ«Ш§Щ„Щ…ШҜШ®Ш§Щ„ШӘвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬iвҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„ШҙШЁЩғШ©вҖ¬.вҖ«ЩҲЩҠШӯШҜШ«вҖ¬вҖ«ШӘШӯШҜЩҠШҜвҖ¬вҖ«Ш§Щ„ЩӮЩҠЩ…вҖ¬вҖ«Ш§Ш§Щ„ШЁШӘШҜШ§ШҰвҖ¬вҖ«ЩҠШ©вҖ¬
вҖ«Щ„ШЈЩ„ЩҲШІШ§ЩҶвҖ¬вҖ«Ш№Щ„ЩҠвҖ¬вҖ«ШЈШіШ§ШівҖ¬вҖ«Ш№ШөШЁЩҲЩҶвҖ¬вҖ«ШЁШ№ШҜвҖ¬вҖ«Ш№ШөШЁЩҲЩҶвҖ¬.
пӮЎвҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬вҖ«Ш§Щ„Ш«Ш§ЩҶЩҠШ©вҖ¬:вҖ«Ш§Щ„ШӘЩҶШҙЩҠШ·вҖ¬
пӮЎвҖ«ШӘЩҶШҙЩҠШ·вҖ¬вҖ«Ш§Ш§Щ„ЩҶШӘШҙШ§ШұвҖ¬вҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬вҖ«Щ„Щ„ШҙШЁЩғШ©вҖ¬вҖ«Ш§Щ„Ш№ШөШЁЩҠШ©вҖ¬вҖ«Ш№ЩҶвҖ¬вҖ«Ш·ШұЩҠЩӮвҖ¬вҖ«ШӘШ·ШЁЩҠЩӮвҖ¬вҖ«Ш§Щ„Щ…ШҜШ®Ш§Щ„ШӘвҖ¬
x1(p),x2(p),вҖҰxn(p)ШҢ
пӮЎвҖ«ЩҲШ§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Ш§Щ„Щ…ШұШәЩҲШЁвҖ¬вҖ«ЩҒЩҠЩҮШ§вҖ¬Yd,1(p) , Yd,2(p) ,вҖҰ.,Yd,n(p)
пҒұвҖ«ЩҲШӯШіШ§ШЁвҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Ш§Щ„ЩҒШ№Щ„ЩҠШ©вҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬:
пӮЎвҖ«ШӯЩҠШ«вҖ¬nвҖ«Щ…ШҜШ®Ш§Щ„ШӘвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬jвҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬ШҢвҖ«ЩҲвҖ¬sigmoidвҖ«ШҜШ§Щ„Ш©вҖ¬вҖ«ШӘЩҶШҙЩҠШ·вҖ¬вҖ«Ш§Ш§Щ„ШівҖ¬
23
пғә
пғә
пғ»
пғ№
пғӘ
пғӘ
пғ«
пғ©
пғҘ
пҖҪ
пҖӯпҖҪ
n
i
jpijwpixsigmoidp
j
y
1
)()()( пҒұ
Dr gafar zen alabdeen salh
(2011)](https://image.slidesharecdn.com/multilayerneuralnetworks-170808125250/85/Multilayer-neural-networks-23-320.jpg)

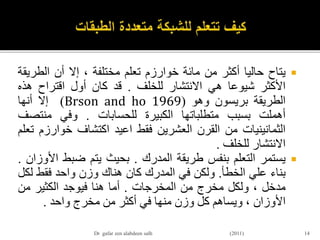
![пӮЎвҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬вҖ«Ш§Щ„Ш«Ш§Щ„Ш«Ш©вҖ¬:вҖ«ШӘШҜШұЩҠШЁвҖ¬вҖ«Ш§ШЈЩ„ЩҲШІШ§ЩҶвҖ¬:вҖ«ШӘШ¬ШҜЩҠШҜвҖ¬вҖ«ШЈЩҲШІШ§ЩҶвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«ШҙШЁЩғШ©вҖ¬вҖ«Ш§Ш§Щ„ЩҶШӘШҙШ§ШұвҖ¬вҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬вҖ«Ш№ЩҶвҖ¬вҖ«Ш·ШұЩҠЩӮвҖ¬вҖ«ЩҶШҙШұвҖ¬вҖ«Ш§ШЈЩ„Ш®Ш·Ш§ШЎвҖ¬вҖ«Ш§Щ„Щ…ШөвҖ¬вҖ«Ш§ШӯШЁШ©вҖ¬
вҖ«Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬
пғҳвҖ«ШӯШіШ§ШЁвҖ¬вҖ«Щ…ЩҠЩ„вҖ¬вҖ«Ш§ЩҲвҖ¬вҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬
пғҳОҙk(p)= yk(p)Г—[1-yk(p)] Г— ek(p)
пғҳвҖ«ШӯЩҠШ«вҖ¬:
пғҳek(p) = Ydk(p) вҖ“Yk(p) where p=1,2,3,вҖҰ
пғҳвҖ«ЩҲШӯШіШ§ШЁвҖ¬вҖ«ШӘШөШӯЩҠШӯвҖ¬вҖ«Ш§Ш§Щ„ЩҲШІШ§ЩҶвҖ¬:
пӮЎWjk (p+1)= wjk(p) +вҲҶWjk (p)
пӮЎвҲҶWjk (p)= ОұГ—yj(p) Г—Оҙk(p)
пғҳвҖ«ЩҲШӘШ¬ШҜЩҠШҜвҖ¬вҖ«Ш§Ш§Щ„ЩҲШІШ§ЩҶвҖ¬вҖ«Ш№ЩҶШҜвҖ¬вҖ«Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬:
пғҳWjk (p+1)= wjk(p) + ОұГ—yj(p) Г—Оҙk(p)
пғҳвҖ«ШӯШіШ§ШЁвҖ¬вҖ«Щ…ЩҠЩ„вҖ¬вҖ«Ш§ЩҲвҖ¬вҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬вҖ«ЩҒЩҠвҖ¬вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬:
пғҳ
пӮЎWij (p+1)= Wij (p) +вҲҶ Wij (p)
пӮЎвҲҶ Wij (p) = ОұГ—Xi(p) Г—Оҙj(p)
пӮЎвҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬вҖ«Ш§Щ„ШұШ§ШЁШ№Ш©вҖ¬:вҖ«Ш§Щ„ШӘЩғШұШ§ШұвҖ¬
пӮЎвҖ«ШІЩҠШ§ШҜШ©вҖ¬вҖ«Ш§Щ„ШӘЩғШұШ§ШұвҖ¬pвҖ«ШЁЩ…ЩӮШҜШ§ШұвҖ¬вҖ«ЩҲШ§ШӯШҜвҖ¬вҖ«ШөШӯЩҠШӯвҖ¬ШҢвҖ«ЩҲШ§Щ„Ш№ЩҲШҜШ©вҖ¬вҖ«Ш§Щ„ЩҠвҖ¬вҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬вҖ«Ш§Щ„Ш«Ш§ЩҶЩҠШ©вҖ¬ШҢвҖ«ЩҲШӘЩғШұШ§ШұвҖ¬вҖ«Ш§Щ„Ш№Щ…Щ„ЩҠШ©вҖ¬вҖ«ШӯШӘЩҠвҖ¬вҖ«ЩҠШӘШӯЩӮЩӮвҖ¬вҖ«Щ…Ш№вҖ¬вҖ«ЩҠШ§ШұвҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬
вҖ«Ш§Щ„Щ…Ш®ШӘШ§ШұвҖ¬
25
Dr gafar zen alabdeen salh
(2011)
пғҘпҖҪ
пӮҙпҖӯпӮҙпҖҪ
I
k
jkkjjj pwppypyp
1
)()()](1[)()( пҒӨпҒӨ](https://image.slidesharecdn.com/multilayerneuralnetworks-170808125250/85/Multilayer-neural-networks-25-320.jpg)
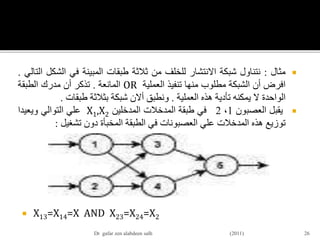

![пӮЎвҖ«Щ„ЩҶШӘЩҶШ§ЩҲЩ„вҖ¬вҖ«ЩҒШҰШ©вҖ¬вҖ«ШӘШҜШұЩҠШЁвҖ¬вҖ«ШӯЩҠШ«вҖ¬X1,X2вҖ«ЩҠШіШ§ЩҲЩҠШ§вҖ¬1ШҢвҖ«ЩҲШ§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Ш§Щ„Щ…ШұШәЩҲШЁвҖ¬
вҖ«ЩҒЩҠЩҮШ§вҖ¬Yd,5вҖ«ШӘШіШ§ЩҲЩҠвҖ¬0вҖ«ЩҲШӘШӯШіШЁвҖ¬вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Ш§Щ„ЩҒШ№Щ„ЩҠШ©вҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶШ§ШӘвҖ¬3вҖ«ЩҲвҖ¬4вҖ«ЩҒЩҠвҖ¬
вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬вҖ«ЩғЩ…Ш§вҖ¬вҖ«ЩҠЩ„ЩҠвҖ¬:
пӮЎ Y3=sigmoid(x1*w13+x2*w23-Оё3)
пӮЎ 1/[1+e-(1*0.5+1*0.4-1*0.8)]=0.5250
пӮЎ Y4=sigmoid(x1*w14+x2*w24-Оё4)
пӮЎ 1/[1+e-(1*0.9+1*1.0+1*0.1)]=0.8808
пӮЎвҖ«ЩҲШ§Ш§Щ„ЩҶвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Ш§Щ„ЩҒШ№Щ„ЩҠШ©вҖ¬ вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ вҖ«ШӘШӘШӯШҜШҜвҖ¬5вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬ вҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«ЩҒЩҠвҖ¬:
пӮЎ Y5=sigmoid(y3*w35+y4*w45-Оё5)
пӮЎ 1/[1+e-(-0.5250*1.2+0.8808*1.1-1*0.3)]=0.5097
28Dr gafar zen alabdeen salh (2011)](https://image.slidesharecdn.com/multilayerneuralnetworks-170808125250/85/Multilayer-neural-networks-28-320.jpg)
![пӮЎ e= yd,5 вҖ“y5 =0-0.5097=-0.5097
пӮЎвҖ«ШӘШҜШұЩҠШЁвҖ¬ вҖ«Ш§Щ„ШӘШ§Щ„ЩҠШ©вҖ¬ вҖ«Ш§Щ„Ш®Ш·ЩҲШ©вҖ¬ вҖ«ЩҲШӘЩғЩҲЩҶвҖ¬вҖ«Ш§Ш§Щ„ЩҲШІШ§ЩҶвҖ¬.вҖ«Щ„ШӘШ¬ШҜЩҠШҜвҖ¬вҖ«Ш§Ш§Щ„ЩҲШІШ§ЩҶвҖ¬ШҢ
вҖ«ШҙШЁЩғШӘЩҶШ§вҖ¬ вҖ«ЩҒЩҠвҖ¬ вҖ«Ш§Щ„Ш№ШӘШЁШ©вҖ¬ вҖ«ЩҲЩ…ШіШӘЩҲЩҠШ§ШӘвҖ¬вҖ«ЩҒШ§ЩҶЩҶШ§вҖ¬вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«ЩҶЩҶШҙШұвҖ¬eвҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«Щ…ЩҶвҖ¬
вҖ«Щ„Щ„Ш®Щ„ЩҒвҖ¬ вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬вҖ«Ш§Щ„ЩҠвҖ¬вҖ«Ш·ШЁЩӮШ©вҖ¬вҖ«Ш§Щ„Щ…ШҜШ®Ш§Щ„ШӘвҖ¬.
пӮЎвҖ«Ш§ЩҲШ§Щ„вҖ¬вҖңвҖ«Щ…ЩҠЩ„вҖ¬ вҖ«ЩҶШӯШіШЁвҖ¬ ШҢвҖ«Ш§ЩҲвҖ¬вҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«Ш§ЩҶШӯШҜШ§ШұвҖ¬5вҖ«Ш·ШЁЩӮШ©вҖ¬ вҖ«ЩҒЩҠвҖ¬
вҖ«Ш§Щ„Щ…Ш®ШұШ¬Ш§ШӘвҖ¬:
пӮЎ Оҙ5= y5Г—[1-y5] Г— e=0.5097*(1-0.5097)*(-0.5097)=-0.1274
пӮЎвҖ«ШЁШ§ЩҒШӘШұШ§Ш¶вҖ¬ вҖ«Ш§Щ„ЩҲШІЩҶвҖ¬ вҖ«ШӘШөШӯЩҠШӯШ§ШӘвҖ¬ вҖ«Ш°Щ„ЩғвҖ¬ вҖ«ШЁШ№ШҜвҖ¬ вҖ«ЩҶШӯШҜШҜвҖ¬ вҖ«Ш«Щ…вҖ¬вҖ«Ш§ЩҶвҖ¬вҖ«Щ…вҖ¬ вҖ«Щ…Ш№Щ„Щ…Ш©вҖ¬вҖ«Ш№ШҜЩ„вҖ¬
вҖ«Ш§Щ„ШӘШ№Щ„Щ…вҖ¬Оұ=0.1
29Dr gafar zen alabdeen salh (2011)](https://image.slidesharecdn.com/multilayerneuralnetworks-170808125250/85/Multilayer-neural-networks-29-320.jpg)
![пӮЎвҖ«Щ„Щ„Ш№ШөШЁЩҲЩҶвҖ¬ вҖ«Ш§Щ„Ш®Ш·ШЈвҖ¬ вҖ«Ш§ЩҶШӯШҜШ§ШұШ§ШӘвҖ¬ вҖ«ШЈЩҲвҖ¬ вҖ«Щ…ЩҠЩҲЩ„вҖ¬ вҖ«Ш°Щ„ЩғвҖ¬ вҖ«ШЁШ№ШҜвҖ¬ вҖ«ЩҶШӯШіШЁвҖ¬3,4вҖ«ЩҒЩҠвҖ¬
вҖ«Ш§Щ„Щ…Ш®ШЁШЈШ©вҖ¬ вҖ«Ш§Щ„Ш·ШЁЩӮШ©вҖ¬:
пӮЎ Оҙ3= y3Г—[1-y3] Г— Оҙ5Г—w35 =0.5250*(1-0.5250)*(-0.1274)*(-
1.2)=0.0381
пӮЎ Оҙ4= y4Г—[1-y4] Г— Оҙ5Г—w45 =0.8808*(1- 0.8808)*(-0.1274)*1.1=-
0.0147
пӮЎвҖ«Ш§ШЈЩ„ЩҲШІШ§ЩҶвҖ¬ вҖ«ШӘШөШӯЩҠШӯШ§ШӘвҖ¬ вҖ«Ш°Щ„ЩғвҖ¬ вҖ«ШЁШ№ШҜвҖ¬ вҖ«ЩҶШӯШҜШҜвҖ¬:
30Dr gafar zen alabdeen salh (2011)](https://image.slidesharecdn.com/multilayerneuralnetworks-170808125250/85/Multilayer-neural-networks-30-320.jpg)