–Ч–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ (11 –Ї–ї–∞—Б)
Download as ppt, pdf0 likes2,327 views
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П –Ј –∞–ї–≥–µ–±—А–Є 11 –Ї–ї–∞—Б
1 of 16
Download to read offline











Ad
Recommended
–†–Њ–Ј–≤"—П–Ј—Г–≤–∞–љ–љ—П –Ј–∞–і–∞—З –љ–∞ –Ј–љ–∞—Е–Њ–і–ґ–µ–љ–љ—П –њ–ї–Њ—Й—Ц —В—А–Є–Ї—Г—В–љ–Є–Ї–∞
–†–Њ–Ј–≤"—П–Ј—Г–≤–∞–љ–љ—П –Ј–∞–і–∞—З –љ–∞ –Ј–љ–∞—Е–Њ–і–ґ–µ–љ–љ—П –њ–ї–Њ—Й—Ц —В—А–Є–Ї—Г—В–љ–Є–Ї–∞sveta7940
ћэ
—Г—А–Њ–Ї–Ч.–Ж.–Ь–µ–і–≤—Ц–і—М. ¬Ђ–Я—А—П–Љ–∞ —В–∞ –Њ–±–µ—А–љ–µ–љ–∞ –њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ—Ц—Б—В—М¬ї (6 –Ї–ї–∞—Б)
–Ч.–Ж.–Ь–µ–і–≤—Ц–і—М. ¬Ђ–Я—А—П–Љ–∞ —В–∞ –Њ–±–µ—А–љ–µ–љ–∞ –њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ—Ц—Б—В—М¬ї (6 –Ї–ї–∞—Б)–Ж–љ—Б—В–Є—В—Г—В –њ—Ц—Б–ї—П–і–Є–њ–ї–Њ–Љ–љ–Њ—Ч –њ–µ–і–∞–≥–Њ–≥—Ц—З–љ–Њ—Ч –Њ—Б–≤—Ц—В–Є –Ъ–£–С–У
ћэ
–Ч.–Ж.–Ь–µ–і–≤—Ц–і—М. ¬Ђ–Я—А—П–Љ–∞ —В–∞ –Њ–±–µ—А–љ–µ–љ–∞ –њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ—Ц—Б—В—М¬ї (6 –Ї–ї–∞—Б)–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–°–Є—Б—В–µ–Љ–Є —А—Ц–≤–љ—П–љ—М –і—А—Г–≥–Њ–≥–Њ —Б—В–µ–њ–µ–љ—П –Ј –і–≤–Њ–Љ–∞ –Ј–Љ—Ц–љ–љ–Є–Љ–Є
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–°–Є—Б—В–µ–Љ–Є —А—Ц–≤–љ—П–љ—М –і—А—Г–≥–Њ–≥–Њ —Б—В–µ–њ–µ–љ—П –Ј –і–≤–Њ–Љ–∞ –Ј–Љ—Ц–љ–љ–Є–Љ–Єsveta7940
ћэ
—Г—А–Њ–Ї—А–Њ–Ј–≤—П–Ј—Г–≤–∞–љ–љ—П —В—А–Є–Ї—Г—В–љ–Є–Ї—Ц–≤ 9 –Ї–ї–∞—Б
—А–Њ–Ј–≤—П–Ј—Г–≤–∞–љ–љ—П —В—А–Є–Ї—Г—В–љ–Є–Ї—Ц–≤ 9 –Ї–ї–∞—Б–Ю–ї—М–≥–∞ –Ъ–Њ—Б—В–µ–љ–Ї–Њ
ћэ
–њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П –і–Њ —Г—А–Њ–Ї—Г –≥–µ–Њ–Љ–µ–Љ–µ—В—А—Ц—Ч –≤ 9 –Ї–ї–∞—Б—Ц –Ј —В–µ–Љ–Є –Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —А–Њ–Ј–≤—П–Ј—Г–≤–∞–љ–љ—П —В—А–Є–Ї—Г—В–љ–Є–Ї—Ц–≤ —Г –њ—А–∞–Ї—В–Є—З–љ–Є—Е –Ј–∞–і–∞—З–∞—Е–†–Њ–Ј–≤вАЩ—П–Ј—Г–≤–∞–љ–љ—П –њ—А–Є–Ї–ї–∞–і–љ–Є—Е –Ј–∞–і–∞—З (—Ц–Ј –Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П–Љ –≤–Є–Ј–љ–∞—З–µ–љ–Њ–≥–Њ —Ц–љ—В–µ–≥—А–∞–ї–∞)
–†–Њ–Ј–≤вАЩ—П–Ј—Г–≤–∞–љ–љ—П –њ—А–Є–Ї–ї–∞–і–љ–Є—Е –Ј–∞–і–∞—З (—Ц–Ј –Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П–Љ –≤–Є–Ј–љ–∞—З–µ–љ–Њ–≥–Њ —Ц–љ—В–µ–≥—А–∞–ї–∞)–Э–∞–і–≤—Ц—А–љ—П–љ—Б—М–Ї–Є–є —Ц–љ—Д–Њ—А–Љ–∞—Ж—Ц–є–љ–Њ - –Љ–µ—В–Њ–і–Є—З–љ–Є–є —Ж–µ–љ—В—А
ћэ
–Ь–∞—АвАЩ—П–љ–∞ –Ф–Њ–ї—Ц—И–љ–∞,
–≤—З–Є—В–µ–ї—М –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –†–Њ–≥–∞—В–Є–љ—Б—М–Ї–Њ—Ч –°–Ч–Ю–® –Ж-–Ж–Ж–Ж —Б—В—Г–њ–µ–љ—Ц–≤ вДЦ 1
–†–Њ–≥–∞—В–Є–љ—Б—М–Ї–Њ—Ч —А–∞–є–Њ–љ–љ–Њ—Ч —А–∞–і–Є –Ж–≤–∞–љ–Њ-–§—А–∞–љ–Ї—Ц–≤—Б—М–Ї–Њ—Ч –Њ–±–ї–∞—Б—В—Ц 8 –Ї–ї–∞—Б —А–∞—Ж—Ц–Њ–љ–∞–ї—М–љ—Ц –і—А–Њ–±–Є.
8 –Ї–ї–∞—Б —А–∞—Ж—Ц–Њ–љ–∞–ї—М–љ—Ц –і—А–Њ–±–Є.Alexandra Gartfil
ћэ
–£ –њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—Ч —А–Њ–Ј–≥–ї—П–љ—Г—В–Њ —В–∞–Ї—Ц –њ–Є—В–∞–љ–љ—П
1)—Ж—Ц–ї—Ц –≤–Є—А–∞–Ј–Є
2)–Ф—А–Њ–±–Њ–≤—Ц –≤–Є—А–∞–Ј–Є
3)–†–∞—Ж—Ц–Њ–љ–∞–ї—М–љ—Ц –≤–Є—А–∞–Ј–Є
4)–Ф–Њ–њ—Г—Б—В–Є–Љ—Ц –Ј–љ–∞—З–µ–љ–љ—П –Ј–Љ—Ц–љ–љ–Є—Е
5)–†–∞—Ж—Ц–Њ–љ–∞–ї—М–љ—Ц –і—А–Њ–±–Є–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–°–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П –Љ—Ц–ґ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —В–∞ –Ї—Г—В–∞–Љ–Є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–°–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П –Љ—Ц–ґ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —В–∞ –Ї—Г—В–∞–Љ–Є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞sveta7940
ћэ
—Г—А–Њ–Ї–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–І–Њ—В–Є—А–Є–Ї—Г—В–љ–Є–Ї–Є (—Г–Ј–∞–≥–∞–ї—М–љ–µ–љ–љ—П —В–∞ —Б–Є—Б—В–µ–Љ–∞—В–Є–Ј–∞—Ж—Ц—П –Ј–љ–∞–љ—М)
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–І–Њ—В–Є—А–Є–Ї—Г—В–љ–Є–Ї–Є (—Г–Ј–∞–≥–∞–ї—М–љ–µ–љ–љ—П —В–∞ —Б–Є—Б—В–µ–Љ–∞—В–Є–Ј–∞—Ж—Ц—П –Ј–љ–∞–љ—М)sveta7940
ћэ
—Г—А–Њ–Ї–Я—А–Є–Ї–ї–∞–і–љ—Ц –Ј–∞–і–∞—З—Ц (–љ–∞ –і–Њ–њ–Њ–Љ–Њ–≥—Г –≤—З–Є—В–µ–ї—О –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є)
–Я—А–Є–Ї–ї–∞–і–љ—Ц –Ј–∞–і–∞—З—Ц (–љ–∞ –і–Њ–њ–Њ–Љ–Њ–≥—Г –≤—З–Є—В–µ–ї—О –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є)–Э–∞–і–≤—Ц—А–љ—П–љ—Б—М–Ї–Є–є —Ц–љ—Д–Њ—А–Љ–∞—Ж—Ц–є–љ–Њ - –Љ–µ—В–Њ–і–Є—З–љ–Є–є —Ж–µ–љ—В—А
ћэ
–Ч–∞–њ—А–Њ–њ–Њ–љ–Њ–≤–∞–љ–Є–є –њ–Њ—Б—Ц–±–љ–Є–Ї –Љ—Ц—Б—В–Є—В—М –њ—А–Є–Ї–ї–∞–і–љ—Ц –Ј–∞–і–∞—З—Ц, –Ј–≥—А—Г–њ–Њ–≤–∞–љ—Ц –њ–Њ –Њ—Б–љ–Њ–≤–љ–Є—Е —В–µ–Љ–∞—Е —Ц –њ—А–Є–Ј–љ–∞—З–µ–љ–Є–є –і–ї—П –≤–Є–Ї–Њ—А–Є—Б—В–∞–љ–љ—П –≤—З–Є—В–µ–ї—П–Љ–Є –њ—А–Є –њ—Ц–і–≥–Њ—В–Њ–≤—Ж—Ц –і–Њ —Г—А–Њ–Ї—Ц–≤ —Г 5 - 11 –Ї–ї–∞—Б–∞—Е.—Б–∞–Љ–Њ—Б—В—Ц–є–љ–∞ —А–Њ–±–Њ—В–∞ –љ–∞ —В–µ–Љ—Г "–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —В–∞ —Ч—Ч –љ–∞—Б–ї—Ц–і–Ї–Є"
—Б–∞–Љ–Њ—Б—В—Ц–є–љ–∞ —А–Њ–±–Њ—В–∞ –љ–∞ —В–µ–Љ—Г "–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —В–∞ —Ч—Ч –љ–∞—Б–ї—Ц–і–Ї–Є"natasha29091997
ћэ
–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤–Я–∞—А–∞–ї–µ–ї—М–љ—Ц—Б—В—М –њ—А—П–Љ–Є—Е —Ц –њ–ї–Њ—Й–Є–љ –≤ –њ—А–Њ—Б—В–Њ—А—Ц
–Я–∞—А–∞–ї–µ–ї—М–љ—Ц—Б—В—М –њ—А—П–Љ–Є—Е —Ц –њ–ї–Њ—Й–Є–љ –≤ –њ—А–Њ—Б—В–Њ—А—Ц–Ы—О–і–Љ–Є–ї–∞ –©–µ—Ж–Њ–≤–∞
ћэ
–Т—Ц–і–љ—Ц–Љ–∞–љ–љ—П —А–∞—Ж—Ц–Њ–љ–∞–ї—М–љ–Є—Е —З–Є—Б–µ–ї
–Т—Ц–і–љ—Ц–Љ–∞–љ–љ—П —А–∞—Ж—Ц–Њ–љ–∞–ї—М–љ–Є—Е —З–Є—Б–µ–ї–Ь–∞—А–Є–љ–∞ –С–∞–ї–і–Њ–≤—Б–Ї–∞—П
ћэ
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П –і–Њ —Г—А–Њ–Ї—Г –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –≤ 5 –Ї–ї–∞—Б—Ц.–њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П —В–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —Ц –Ї–Њ–љ—Г—Б—Ц–≤.pptx
–њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П —В–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —Ц –Ї–Њ–љ—Г—Б—Ц–≤.pptxssuser908bb6
ћэ
–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —Ц –Ї–Њ—Б–Є–љ—Г—Б—Ц–≤9–Ї–ї. –Ї–≤–∞–і—А–∞—В–љ—Ц –љ–µ—А—Ц–≤–љ–Њ—Б—В—Ц
9–Ї–ї. –Ї–≤–∞–і—А–∞—В–љ—Ц –љ–µ—А—Ц–≤–љ–Њ—Б—В—ЦPasha Boyko
ћэ
9–Ї–ї. –Ї–≤–∞–і—А–∞—В–љ—Ц –љ–µ—А—Ц–≤–љ–Њ—Б—В—Ц–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц —В–∞ –є–Њ–≥–Њ –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц. –У–Њ–Љ–Њ—В–µ—В—Ц—П.
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц —В–∞ –є–Њ–≥–Њ –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц. –У–Њ–Љ–Њ—В–µ—В—Ц—П.sveta7940
ћэ
—Г—А–Њ–Ї–Т–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї —В–∞ –є–Њ–≥–Њ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є–є –Ј–Љ—Ц—Б—В
–Т–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї —В–∞ –є–Њ–≥–Њ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є–є –Ј–Љ—Ц—Б—ВFormula.co.ua
ћэ
–Ь–µ—В–∞ —Г—А–Њ–Ї—Г: —Б—Д–Њ—А–Љ—Г–ї—О–≤–∞—В–Є –њ–Њ–љ—П—В—В—П –Ї—А–Є–≤–Њ–ї—Ц–љ—Ц–є–љ–Њ—Ч —В—А–∞–њ–µ—Ж—Ц—Ч —В–∞ –≤–Є–Ј–љ–∞—З–µ–љ–Њ–≥–Њ —Ц–љ—В–µ–≥—А–∞–ї–∞; –і–Њ–Љ–Њ–≥—В–Є—Б—П –Ј–∞—Б–≤–Њ—Ф–љ–љ—П —Д–Њ—А–Љ—Г–ї–Є –Э—М—О—В–Њ–љ–∞-–Ы–µ–є–±–љ—Ц—Ж–∞ —Ц –≤–ї–∞—Б—В–Є–≤–Њ—Б—В–µ–є –≤–Є–Ј–љ–∞—З–µ–љ–Њ–≥–Њ —Ц–љ—В–µ–≥—А–∞–ї–∞.–Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –Њ–±'—Ф–Љ—Ц–≤ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Ц–≥—Г—А
–Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –Њ–±'—Ф–Љ—Ц–≤ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Ц–≥—Г—А–°–≤–µ—В–ї–∞–љ–∞ –Ю–ї–µ–є–љ–Є–Ї
ћэ
–Ж–љ—В–µ–≥—А–∞–ї –Ј–∞—Б—В–Њ—Б–Њ–≤—Г—О—В—М –і–ї—П –Њ–±—З–Є—Б–ї–µ–љ—М —Ц –≤ –Љ–∞—В–µ–Љ–∞—В–Є—Ж—Ц, —Ц –≤ —Д—Ц–Ј–Є—Ж—Ц, —Ц –≤ –µ–Ї–Њ–љ–Њ–Љ—Ц—Ж—Ц...More Related Content
What's hot (20)
8 –Ї–ї–∞—Б —А–∞—Ж—Ц–Њ–љ–∞–ї—М–љ—Ц –і—А–Њ–±–Є.
8 –Ї–ї–∞—Б —А–∞—Ж—Ц–Њ–љ–∞–ї—М–љ—Ц –і—А–Њ–±–Є.Alexandra Gartfil
ћэ
–£ –њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—Ч —А–Њ–Ј–≥–ї—П–љ—Г—В–Њ —В–∞–Ї—Ц –њ–Є—В–∞–љ–љ—П
1)—Ж—Ц–ї—Ц –≤–Є—А–∞–Ј–Є
2)–Ф—А–Њ–±–Њ–≤—Ц –≤–Є—А–∞–Ј–Є
3)–†–∞—Ж—Ц–Њ–љ–∞–ї—М–љ—Ц –≤–Є—А–∞–Ј–Є
4)–Ф–Њ–њ—Г—Б—В–Є–Љ—Ц –Ј–љ–∞—З–µ–љ–љ—П –Ј–Љ—Ц–љ–љ–Є—Е
5)–†–∞—Ж—Ц–Њ–љ–∞–ї—М–љ—Ц –і—А–Њ–±–Є–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–°–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П –Љ—Ц–ґ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —В–∞ –Ї—Г—В–∞–Љ–Є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–°–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П –Љ—Ц–ґ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —В–∞ –Ї—Г—В–∞–Љ–Є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞sveta7940
ћэ
—Г—А–Њ–Ї–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–І–Њ—В–Є—А–Є–Ї—Г—В–љ–Є–Ї–Є (—Г–Ј–∞–≥–∞–ї—М–љ–µ–љ–љ—П —В–∞ —Б–Є—Б—В–µ–Љ–∞—В–Є–Ј–∞—Ж—Ц—П –Ј–љ–∞–љ—М)
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–І–Њ—В–Є—А–Є–Ї—Г—В–љ–Є–Ї–Є (—Г–Ј–∞–≥–∞–ї—М–љ–µ–љ–љ—П —В–∞ —Б–Є—Б—В–µ–Љ–∞—В–Є–Ј–∞—Ж—Ц—П –Ј–љ–∞–љ—М)sveta7940
ћэ
—Г—А–Њ–Ї–Я—А–Є–Ї–ї–∞–і–љ—Ц –Ј–∞–і–∞—З—Ц (–љ–∞ –і–Њ–њ–Њ–Љ–Њ–≥—Г –≤—З–Є—В–µ–ї—О –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є)
–Я—А–Є–Ї–ї–∞–і–љ—Ц –Ј–∞–і–∞—З—Ц (–љ–∞ –і–Њ–њ–Њ–Љ–Њ–≥—Г –≤—З–Є—В–µ–ї—О –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є)–Э–∞–і–≤—Ц—А–љ—П–љ—Б—М–Ї–Є–є —Ц–љ—Д–Њ—А–Љ–∞—Ж—Ц–є–љ–Њ - –Љ–µ—В–Њ–і–Є—З–љ–Є–є —Ж–µ–љ—В—А
ћэ
–Ч–∞–њ—А–Њ–њ–Њ–љ–Њ–≤–∞–љ–Є–є –њ–Њ—Б—Ц–±–љ–Є–Ї –Љ—Ц—Б—В–Є—В—М –њ—А–Є–Ї–ї–∞–і–љ—Ц –Ј–∞–і–∞—З—Ц, –Ј–≥—А—Г–њ–Њ–≤–∞–љ—Ц –њ–Њ –Њ—Б–љ–Њ–≤–љ–Є—Е —В–µ–Љ–∞—Е —Ц –њ—А–Є–Ј–љ–∞—З–µ–љ–Є–є –і–ї—П –≤–Є–Ї–Њ—А–Є—Б—В–∞–љ–љ—П –≤—З–Є—В–µ–ї—П–Љ–Є –њ—А–Є –њ—Ц–і–≥–Њ—В–Њ–≤—Ж—Ц –і–Њ —Г—А–Њ–Ї—Ц–≤ —Г 5 - 11 –Ї–ї–∞—Б–∞—Е.—Б–∞–Љ–Њ—Б—В—Ц–є–љ–∞ —А–Њ–±–Њ—В–∞ –љ–∞ —В–µ–Љ—Г "–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —В–∞ —Ч—Ч –љ–∞—Б–ї—Ц–і–Ї–Є"
—Б–∞–Љ–Њ—Б—В—Ц–є–љ–∞ —А–Њ–±–Њ—В–∞ –љ–∞ —В–µ–Љ—Г "–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —В–∞ —Ч—Ч –љ–∞—Б–ї—Ц–і–Ї–Є"natasha29091997
ћэ
–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤–Я–∞—А–∞–ї–µ–ї—М–љ—Ц—Б—В—М –њ—А—П–Љ–Є—Е —Ц –њ–ї–Њ—Й–Є–љ –≤ –њ—А–Њ—Б—В–Њ—А—Ц
–Я–∞—А–∞–ї–µ–ї—М–љ—Ц—Б—В—М –њ—А—П–Љ–Є—Е —Ц –њ–ї–Њ—Й–Є–љ –≤ –њ—А–Њ—Б—В–Њ—А—Ц–Ы—О–і–Љ–Є–ї–∞ –©–µ—Ж–Њ–≤–∞
ћэ
–Т—Ц–і–љ—Ц–Љ–∞–љ–љ—П —А–∞—Ж—Ц–Њ–љ–∞–ї—М–љ–Є—Е —З–Є—Б–µ–ї
–Т—Ц–і–љ—Ц–Љ–∞–љ–љ—П —А–∞—Ж—Ц–Њ–љ–∞–ї—М–љ–Є—Е —З–Є—Б–µ–ї–Ь–∞—А–Є–љ–∞ –С–∞–ї–і–Њ–≤—Б–Ї–∞—П
ћэ
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П –і–Њ —Г—А–Њ–Ї—Г –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –≤ 5 –Ї–ї–∞—Б—Ц.–њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П —В–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —Ц –Ї–Њ–љ—Г—Б—Ц–≤.pptx
–њ—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П —В–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —Ц –Ї–Њ–љ—Г—Б—Ц–≤.pptxssuser908bb6
ћэ
–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —Ц –Ї–Њ—Б–Є–љ—Г—Б—Ц–≤9–Ї–ї. –Ї–≤–∞–і—А–∞—В–љ—Ц –љ–µ—А—Ц–≤–љ–Њ—Б—В—Ц
9–Ї–ї. –Ї–≤–∞–і—А–∞—В–љ—Ц –љ–µ—А—Ц–≤–љ–Њ—Б—В—ЦPasha Boyko
ћэ
9–Ї–ї. –Ї–≤–∞–і—А–∞—В–љ—Ц –љ–µ—А—Ц–≤–љ–Њ—Б—В—Ц–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц —В–∞ –є–Њ–≥–Њ –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц. –У–Њ–Љ–Њ—В–µ—В—Ц—П.
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц —В–∞ –є–Њ–≥–Њ –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц. –У–Њ–Љ–Њ—В–µ—В—Ц—П.sveta7940
ћэ
—Г—А–Њ–Ї–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–°–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П –Љ—Ц–ґ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —В–∞ –Ї—Г—В–∞–Љ–Є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–°–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П –Љ—Ц–ґ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —В–∞ –Ї—Г—В–∞–Љ–Є –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞sveta7940
ћэ
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–І–Њ—В–Є—А–Є–Ї—Г—В–љ–Є–Ї–Є (—Г–Ј–∞–≥–∞–ї—М–љ–µ–љ–љ—П —В–∞ —Б–Є—Б—В–µ–Љ–∞—В–Є–Ј–∞—Ж—Ц—П –Ј–љ–∞–љ—М)
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–І–Њ—В–Є—А–Є–Ї—Г—В–љ–Є–Ї–Є (—Г–Ј–∞–≥–∞–ї—М–љ–µ–љ–љ—П —В–∞ —Б–Є—Б—В–µ–Љ–∞—В–Є–Ј–∞—Ж—Ц—П –Ј–љ–∞–љ—М)sveta7940
ћэ
–Я—А–Є–Ї–ї–∞–і–љ—Ц –Ј–∞–і–∞—З—Ц (–љ–∞ –і–Њ–њ–Њ–Љ–Њ–≥—Г –≤—З–Є—В–µ–ї—О –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є)
–Я—А–Є–Ї–ї–∞–і–љ—Ц –Ј–∞–і–∞—З—Ц (–љ–∞ –і–Њ–њ–Њ–Љ–Њ–≥—Г –≤—З–Є—В–µ–ї—О –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є)–Э–∞–і–≤—Ц—А–љ—П–љ—Б—М–Ї–Є–є —Ц–љ—Д–Њ—А–Љ–∞—Ж—Ц–є–љ–Њ - –Љ–µ—В–Њ–і–Є—З–љ–Є–є —Ж–µ–љ—В—А
ћэ
—Б–∞–Љ–Њ—Б—В—Ц–є–љ–∞ —А–Њ–±–Њ—В–∞ –љ–∞ —В–µ–Љ—Г "–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —В–∞ —Ч—Ч –љ–∞—Б–ї—Ц–і–Ї–Є"
—Б–∞–Љ–Њ—Б—В—Ц–є–љ–∞ —А–Њ–±–Њ—В–∞ –љ–∞ —В–µ–Љ—Г "–Ґ–µ–Њ—А–µ–Љ–∞ —Б–Є–љ—Г—Б—Ц–≤ —В–∞ —Ч—Ч –љ–∞—Б–ї—Ц–і–Ї–Є"natasha29091997
ћэ
–Я–∞—А–∞–ї–µ–ї—М–љ—Ц—Б—В—М –њ—А—П–Љ–Є—Е —Ц –њ–ї–Њ—Й–Є–љ –≤ –њ—А–Њ—Б—В–Њ—А—Ц
–Я–∞—А–∞–ї–µ–ї—М–љ—Ц—Б—В—М –њ—А—П–Љ–Є—Е —Ц –њ–ї–Њ—Й–Є–љ –≤ –њ—А–Њ—Б—В–Њ—А—Ц–Ы—О–і–Љ–Є–ї–∞ –©–µ—Ж–Њ–≤–∞
ћэ
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц —В–∞ –є–Њ–≥–Њ –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц. –У–Њ–Љ–Њ—В–µ—В—Ц—П.
–Я—А–µ–Ј–µ–љ—В–∞—Ж—Ц—П:–Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –њ–Њ–і—Ц–±–љ–Њ—Б—В—Ц —В–∞ –є–Њ–≥–Њ –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц. –У–Њ–Љ–Њ—В–µ—В—Ц—П.sveta7940
ћэ
Similar to –Ч–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ (11 –Ї–ї–∞—Б) (20)
–Т–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї —В–∞ –є–Њ–≥–Њ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є–є –Ј–Љ—Ц—Б—В
–Т–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї —В–∞ –є–Њ–≥–Њ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є–є –Ј–Љ—Ц—Б—ВFormula.co.ua
ћэ
–Ь–µ—В–∞ —Г—А–Њ–Ї—Г: —Б—Д–Њ—А–Љ—Г–ї—О–≤–∞—В–Є –њ–Њ–љ—П—В—В—П –Ї—А–Є–≤–Њ–ї—Ц–љ—Ц–є–љ–Њ—Ч —В—А–∞–њ–µ—Ж—Ц—Ч —В–∞ –≤–Є–Ј–љ–∞—З–µ–љ–Њ–≥–Њ —Ц–љ—В–µ–≥—А–∞–ї–∞; –і–Њ–Љ–Њ–≥—В–Є—Б—П –Ј–∞—Б–≤–Њ—Ф–љ–љ—П —Д–Њ—А–Љ—Г–ї–Є –Э—М—О—В–Њ–љ–∞-–Ы–µ–є–±–љ—Ц—Ж–∞ —Ц –≤–ї–∞—Б—В–Є–≤–Њ—Б—В–µ–є –≤–Є–Ј–љ–∞—З–µ–љ–Њ–≥–Њ —Ц–љ—В–µ–≥—А–∞–ї–∞.–Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –Њ–±'—Ф–Љ—Ц–≤ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Ц–≥—Г—А
–Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –Њ–±'—Ф–Љ—Ц–≤ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Ц–≥—Г—А–°–≤–µ—В–ї–∞–љ–∞ –Ю–ї–µ–є–љ–Є–Ї
ћэ
–Ж–љ—В–µ–≥—А–∞–ї –Ј–∞—Б—В–Њ—Б–Њ–≤—Г—О—В—М –і–ї—П –Њ–±—З–Є—Б–ї–µ–љ—М —Ц –≤ –Љ–∞—В–µ–Љ–∞—В–Є—Ж—Ц, —Ц –≤ —Д—Ц–Ј–Є—Ж—Ц, —Ц –≤ –µ–Ї–Њ–љ–Њ–Љ—Ц—Ж—Ц...Praktichne zastosuvannya _zag_vidomosti__isto
Praktichne zastosuvannya _zag_vidomosti__istoVlad Chervinchuk
ћэ
Praktichne zastosuvannya _zag_vidomosti__isto–Ч–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –њ–ї–Њ—Й –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Ц–≥—Г—А
–Ч–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –њ–ї–Њ—Й –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Ц–≥—Г—А–°–≤–µ—В–ї–∞–љ–∞ –Ю–ї–µ–є–љ–Є–Ї
ћэ
–Ж–љ—В–µ–≥—А–∞–ї —В–∞ –є–Њ–≥–Њ –Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П–Ї–Њ–њ–Є—П –≤–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї. —Д–Њ—А–Љ—Г–ї–∞ –љ—М—О—В–Њ–љ–∞ –ї–µ–є–±–љ—Ц—Ж–∞
–Ї–Њ–њ–Є—П –≤–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї. —Д–Њ—А–Љ—Г–ї–∞ –љ—М—О—В–Њ–љ–∞ –ї–µ–є–±–љ—Ц—Ж–∞Veselovwww
ћэ
–Ж–љ—В–µ–≥—А–∞–ї —В–∞ –є–Њ–≥–Њ –Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П
–Ж–љ—В–µ–≥—А–∞–ї —В–∞ –є–Њ–≥–Њ –Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—Пrussoua
ћэ
–Я—Ц–і—Б—Г–Љ–Ї–Њ–≤–Є–є —Г—А–Њ–Ї –Ј –∞–ї–≥–µ–±—А–Є —Г 11 –Ї–ї–∞—Б—Ц–Т–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї —В–∞ –є–Њ–≥–Њ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є–є –Ј–Љ—Ц—Б—В
–Т–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї —В–∞ –є–Њ–≥–Њ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є–є –Ј–Љ—Ц—Б—ВFormula.co.ua
ћэ
–Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –Њ–±'—Ф–Љ—Ц–≤ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Ц–≥—Г—А
–Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –Њ–±'—Ф–Љ—Ц–≤ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Ц–≥—Г—А–°–≤–µ—В–ї–∞–љ–∞ –Ю–ї–µ–є–љ–Є–Ї
ћэ
–Ч–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –њ–ї–Њ—Й –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Ц–≥—Г—А
–Ч–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –њ–ї–Њ—Й –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—Е —Д—Ц–≥—Г—А–°–≤–µ—В–ї–∞–љ–∞ –Ю–ї–µ–є–љ–Є–Ї
ћэ
–Ї–Њ–њ–Є—П –≤–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї. —Д–Њ—А–Љ—Г–ї–∞ –љ—М—О—В–Њ–љ–∞ –ї–µ–є–±–љ—Ц—Ж–∞
–Ї–Њ–њ–Є—П –≤–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї. —Д–Њ—А–Љ—Г–ї–∞ –љ—М—О—В–Њ–љ–∞ –ї–µ–є–±–љ—Ц—Ж–∞Veselovwww
ћэ
Ad
More from Olexandr Lazarets (20)
–Ч–Т–Ж–Ґ –Ф–Ш–†–Х–Ъ–Ґ–Ю–†–Р 2016-2017
–Ч–Т–Ж–Ґ –Ф–Ш–†–Х–Ъ–Ґ–Ю–†–Р 2016-2017Olexandr Lazarets
ћэ
–Ч–Т–Ж–Ґ –Ф–Ш–†–Х–Ъ–Ґ–Ю–†–Р
–С–µ—А–µ–Ј–љ—Ц–≤—Б—М–Ї–Њ–≥–Њ –љ–∞–≤—З–∞–ї—М–љ–Њ-–≤–Є—Е–Њ–≤–љ–Њ–≥–Њ –Ї–Њ–Љ–њ–ї–µ–Ї—Б—Г
¬Ђ–Х–Ї–Њ–љ–Њ–Љ—Ц–Ї–Њ-–≥—Г–Љ–∞–љ—Ц—В–∞—А–љ–Є–є –ї—Ц—Ж–µ–є вАУ –Ј–∞–≥–∞–ї—М–љ–Њ–Њ—Б–≤—Ц—В–љ—П —И–Ї–Њ–ї–∞
–Ж-–Ж–Ж —Б—В—Г–њ–µ–љ—Ц–≤¬ї
–Ј–∞ –њ—Ц–і—Б—Г–Љ–Ї–∞–Љ–Є 2016/2017 –љ–∞–≤—З–∞–ї—М–љ–Њ–≥–Њ —А–Њ–Ї—Г
–Э–∞–Ї–∞–Ј –њ—А–Њ –Ј–∞—А–∞—Е—Г–≤–∞–љ–љ—П –љ–∞ –µ–Ї—Б—В–µ—А–љ–∞—В–љ—Г —Д–Њ—А–Љ—Г –љ–∞–≤—З–∞–љ–љ—П
–Э–∞–Ї–∞–Ј –њ—А–Њ –Ј–∞—А–∞—Е—Г–≤–∞–љ–љ—П –љ–∞ –µ–Ї—Б—В–µ—А–љ–∞—В–љ—Г —Д–Њ—А–Љ—Г –љ–∞–≤—З–∞–љ–љ—ПOlexandr Lazarets
ћэ
–Э–∞–Ї–∞–Ј –њ—А–Њ –Ј–∞—А–∞—Е—Г–≤–∞–љ–љ—П –љ–∞ –µ–Ї—Б—В–µ—А–љ–∞—В–љ—Г —Д–Њ—А–Љ—Г –љ–∞–≤—З–∞–љ–љ—П–Ч–≤—Ц—В –њ—А–Њ –≤–Є–Ї–Њ—А–Є—Б—В–∞–љ–љ—П —Ц –љ–∞–і—Е–Њ–і–ґ–µ–љ–љ—П –Ї–Њ—И—В—Ц–≤ –Ј–∞ —Ц—Ц—Ц –Ї–≤–∞—А—В–∞–ї 2017 —А–Њ–Ї—Г
–Ч–≤—Ц—В –њ—А–Њ –≤–Є–Ї–Њ—А–Є—Б—В–∞–љ–љ—П —Ц –љ–∞–і—Е–Њ–і–ґ–µ–љ–љ—П –Ї–Њ—И—В—Ц–≤ –Ј–∞ —Ц—Ц—Ц –Ї–≤–∞—А—В–∞–ї 2017 —А–Њ–Ї—ГOlexandr Lazarets
ћэ
–Ч–≤—Ц—В –њ—А–Њ –≤–Є–Ї–Њ—А–Є—Б—В–∞–љ–љ—П —Ц –љ–∞–і—Е–Њ–і–ґ–µ–љ–љ—П –Ї–Њ—И—В—Ц–≤ –Ј–∞ —Ц—Ц—Ц –Ї–≤–∞—А—В–∞–ї 2017 —А–Њ–Ї—Г–С–∞–ї–∞–љ—Б –Э–Т–Ъ
–С–∞–ї–∞–љ—Б –Э–Т–ЪOlexandr Lazarets
ћэ
–§—Ц–љ–∞–љ—Б–Њ–≤–Є–є –±–∞–ї–∞–љ—Б –С–µ—А–µ–Ј–љ—Ц–≤—Б—М–Ї–Њ–≥–Њ –Э–Т–Ъ—Д—Ц–љ–∞–љ—Б–Њ–≤–∞ –Ј–≤—Ц—В–љ—Ц—Б—В—М
—Д—Ц–љ–∞–љ—Б–Њ–≤–∞ –Ј–≤—Ц—В–љ—Ц—Б—В—МOlexandr Lazarets
ћэ
–§—Ц–љ–∞–љ—Б–Њ–≤–∞ –Ј–≤—Ц—В–љ—Ц—Б—В—М –С–µ—А–µ–Ј–љ—Ц–≤—Б—М–Ї–Њ–≥–Њ –Э–Т–Ъ–Ї–Њ—И—В–Њ—А–Є—Б 2
–Ї–Њ—И—В–Њ—А–Є—Б 2Olexandr Lazarets
ћэ
–Ъ–Њ—И—В–Њ—А–Є—Б –Ј–∞ 2017 —А—Ц–Ї –С–µ—А–µ–Ј–љ—Ц–≤—Б—М–Ї–Њ–≥–Њ –Э–Т–Ъ "–Х–У–Ы-–Ч–Ю–®"–Ї–Њ—И—В–Њ—А–Є—Б –Ј–∞ 2017 —А—Ц–Ї
–Ї–Њ—И—В–Њ—А–Є—Б –Ј–∞ 2017 —А—Ц–Ї Olexandr Lazarets
ћэ
–Ъ–Њ—И—В–Њ—А–Є—Б –Ј–∞ 2017 —А—Ц–Ї –С–µ—А–µ–Ј–љ—Ц–≤—Б—М–Ї–Њ–≥–Њ –Э–Т–Ъ "–Х–У–Ы-–Х–У–Ы"–Э–∞–Ї–∞–Ј –њ—А–Њ –≤—Ц–і—А–∞—Е—Г–≤–∞–љ–љ—П
–Э–∞–Ї–∞–Ј –њ—А–Њ –≤—Ц–і—А–∞—Е—Г–≤–∞–љ–љ—ПOlexandr Lazarets
ћэ
–Э–∞–Ї–∞–Ј –њ—А–Њ –≤—Ц–і—А–∞—Е—Г–≤–∞–љ–љ—П–Ј–≤—Ц—В –і–Є—А–µ–Ї—В–Њ—А–∞ 2017 —А—Ц–Ї
–Ј–≤—Ц—В –і–Є—А–µ–Ї—В–Њ—А–∞ 2017 —А—Ц–ЇOlexandr Lazarets
ћэ
–Ч–Т–Ж–Ґ –Ф–Ш–†–Х–Ъ–Ґ–Ю–†–Р
–С–µ—А–µ–Ј–љ—Ц–≤—Б—М–Ї–Њ–≥–Њ –љ–∞–≤—З–∞–ї—М–љ–Њ-–≤–Є—Е–Њ–≤–љ–Њ–≥–Њ –Ї–Њ–Љ–њ–ї–µ–Ї—Б—Г
¬Ђ–Х–Ї–Њ–љ–Њ–Љ—Ц–Ї–Њ-–≥—Г–Љ–∞–љ—Ц—В–∞—А–љ–Є–є –ї—Ц—Ж–µ–є вАУ –Ј–∞–≥–∞–ї—М–љ–Њ–Њ—Б–≤—Ц—В–љ—П —И–Ї–Њ–ї–∞
–Ж-–Ж–Ж —Б—В—Г–њ–µ–љ—Ц–≤¬ї
–Ј–∞ –њ—Ц–і—Б—Г–Љ–Ї–∞–Љ–Є 2016/2017 –љ–∞–≤—З–∞–ї—М–љ–Њ–≥–Њ —А–Њ–Ї—Г
–Ч—А–∞–Ј–Њ–Ї –≤—Б—В—Г–њ–љ–Њ–≥–Њ –≤–Є–њ—А–Њ–±–Њ–≤—Г–≤–∞–љ–љ—П –Ј –∞–љ–≥–ї—Ц–є—Б—М–Ї–Њ—Ч –Љ–Њ–≤–Є (10 –Ї–ї–∞—Б, –≥—Г–Љ–∞–љ—Ц—В–∞—А–љ–Є–є –њ—А–Њ...
–Ч—А–∞–Ј–Њ–Ї –≤—Б—В—Г–њ–љ–Њ–≥–Њ –≤–Є–њ—А–Њ–±–Њ–≤—Г–≤–∞–љ–љ—П –Ј –∞–љ–≥–ї—Ц–є—Б—М–Ї–Њ—Ч –Љ–Њ–≤–Є (10 –Ї–ї–∞—Б, –≥—Г–Љ–∞–љ—Ц—В–∞—А–љ–Є–є –њ—А–Њ...Olexandr Lazarets
ћэ
111–Ј—А–∞–Ј–Њ–Ї –≤—Б—В—Г–њ–љ–Њ–≥–Њ-–≤–Є–њ—А–Њ–±–Њ–≤—Г–≤–∞–љ–љ—П-–Ј-–Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є
–Ј—А–∞–Ј–Њ–Ї –≤—Б—В—Г–њ–љ–Њ–≥–Њ-–≤–Є–њ—А–Њ–±–Њ–≤—Г–≤–∞–љ–љ—П-–Ј-–Љ–∞—В–µ–Љ–∞—В–Є–Ї–ЄOlexandr Lazarets
ћэ
111–њ—А–∞–≤–Є–ї–∞ –Ї–Њ–љ–Ї—Г—А—Б–љ–Њ–≥–Њ –њ—А–Є–є–Љ–∞–љ–љ—П_–і–Њ_–їi—Ж–µ–є–љ–Є—Е_–Ї–ї–∞—Бi–≤_–±–µ—А–µ–Ј–љi–≤—Б_–Ї–Њ–≥–Њ_–љ–≤–Ї
–њ—А–∞–≤–Є–ї–∞ –Ї–Њ–љ–Ї—Г—А—Б–љ–Њ–≥–Њ –њ—А–Є–є–Љ–∞–љ–љ—П_–і–Њ_–їi—Ж–µ–є–љ–Є—Е_–Ї–ї–∞—Бi–≤_–±–µ—А–µ–Ј–љi–≤—Б_–Ї–Њ–≥–Њ_–љ–≤–ЇOlexandr Lazarets
ћэ
1Dekada
DekadaOlexandr Lazarets
ћэ
–Ф–µ–Ї–∞–і–∞ –Ї–∞—Д–µ–і—А–Є —В–Њ—З–љ–Є—Е –љ–∞—Г–Ї –Х–Ї–Њ–љ–Њ–Љ—Ц–Ї–Њ-–≥—Г–Љ–∞–љ—Ц—В–∞—А–љ–Њ–≥–Њ –ї—Ц—Ж–µ—О–Э–∞–Ї–∞–Ј –њ—А–Њ –Ј–∞—А–∞—Е—Г–≤–∞–љ–љ—П –љ–∞ –µ–Ї—Б—В–µ—А–љ–∞—В–љ—Г —Д–Њ—А–Љ—Г –љ–∞–≤—З–∞–љ–љ—П
–Э–∞–Ї–∞–Ј –њ—А–Њ –Ј–∞—А–∞—Е—Г–≤–∞–љ–љ—П –љ–∞ –µ–Ї—Б—В–µ—А–љ–∞—В–љ—Г —Д–Њ—А–Љ—Г –љ–∞–≤—З–∞–љ–љ—ПOlexandr Lazarets
ћэ
–Ч–≤—Ц—В –њ—А–Њ –≤–Є–Ї–Њ—А–Є—Б—В–∞–љ–љ—П —Ц –љ–∞–і—Е–Њ–і–ґ–µ–љ–љ—П –Ї–Њ—И—В—Ц–≤ –Ј–∞ —Ц—Ц—Ц –Ї–≤–∞—А—В–∞–ї 2017 —А–Њ–Ї—Г
–Ч–≤—Ц—В –њ—А–Њ –≤–Є–Ї–Њ—А–Є—Б—В–∞–љ–љ—П —Ц –љ–∞–і—Е–Њ–і–ґ–µ–љ–љ—П –Ї–Њ—И—В—Ц–≤ –Ј–∞ —Ц—Ц—Ц –Ї–≤–∞—А—В–∞–ї 2017 —А–Њ–Ї—ГOlexandr Lazarets
ћэ
–Ч—А–∞–Ј–Њ–Ї –≤—Б—В—Г–њ–љ–Њ–≥–Њ –≤–Є–њ—А–Њ–±–Њ–≤—Г–≤–∞–љ–љ—П –Ј –∞–љ–≥–ї—Ц–є—Б—М–Ї–Њ—Ч –Љ–Њ–≤–Є (10 –Ї–ї–∞—Б, –≥—Г–Љ–∞–љ—Ц—В–∞—А–љ–Є–є –њ—А–Њ...
–Ч—А–∞–Ј–Њ–Ї –≤—Б—В—Г–њ–љ–Њ–≥–Њ –≤–Є–њ—А–Њ–±–Њ–≤—Г–≤–∞–љ–љ—П –Ј –∞–љ–≥–ї—Ц–є—Б—М–Ї–Њ—Ч –Љ–Њ–≤–Є (10 –Ї–ї–∞—Б, –≥—Г–Љ–∞–љ—Ц—В–∞—А–љ–Є–є –њ—А–Њ...Olexandr Lazarets
ћэ
–Ј—А–∞–Ј–Њ–Ї –≤—Б—В—Г–њ–љ–Њ–≥–Њ-–≤–Є–њ—А–Њ–±–Њ–≤—Г–≤–∞–љ–љ—П-–Ј-–Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є
–Ј—А–∞–Ј–Њ–Ї –≤—Б—В—Г–њ–љ–Њ–≥–Њ-–≤–Є–њ—А–Њ–±–Њ–≤—Г–≤–∞–љ–љ—П-–Ј-–Љ–∞—В–µ–Љ–∞—В–Є–Ї–ЄOlexandr Lazarets
ћэ
–њ—А–∞–≤–Є–ї–∞ –Ї–Њ–љ–Ї—Г—А—Б–љ–Њ–≥–Њ –њ—А–Є–є–Љ–∞–љ–љ—П_–і–Њ_–їi—Ж–µ–є–љ–Є—Е_–Ї–ї–∞—Бi–≤_–±–µ—А–µ–Ј–љi–≤—Б_–Ї–Њ–≥–Њ_–љ–≤–Ї
–њ—А–∞–≤–Є–ї–∞ –Ї–Њ–љ–Ї—Г—А—Б–љ–Њ–≥–Њ –њ—А–Є–є–Љ–∞–љ–љ—П_–і–Њ_–їi—Ж–µ–є–љ–Є—Е_–Ї–ї–∞—Бi–≤_–±–µ—А–µ–Ј–љi–≤—Б_–Ї–Њ–≥–Њ_–љ–≤–ЇOlexandr Lazarets
ћэ
Ad
Recently uploaded (7)
–Ч–≤—Ц—В_–Ъ—Г—А–∞–Ї—Ц–љ –Ю.–Ь. _2025_1750399483.pptx
–Ч–≤—Ц—В_–Ъ—Г—А–∞–Ї—Ц–љ –Ю.–Ь. _2025_1750399483.pptxrt270588
ћэ
–Ч–≤—Ц—В –≤.–Њ.–і–Є—А–µ–Ї—В–Њ—А–∞ –≥—Ц–Љ–љ–∞–Ј—Ц—Ч–Ч–Т–Ж–Ґ –Ъ–Х–†–Ж–Т–Э–Ш–Ъ–Р –І–Ю–†–Э–Ю–Ь–Ю–†–°–ђ–Ъ–Ю–У–Ю –Ы–Ж–¶–Х–Ѓ вДЦ3 2025.pptx
–Ч–Т–Ж–Ґ –Ъ–Х–†–Ж–Т–Э–Ш–Ъ–Р –І–Ю–†–Э–Ю–Ь–Ю–†–°–ђ–Ъ–Ю–У–Ю –Ы–Ж–¶–Х–Ѓ вДЦ3 2025.pptxssuserb90919
ћэ
–Ч–Т–Ж–Ґ –Ъ–Х–†–Ж–Т–Э–Ш–Ъ–Р –І–Ю–†–Э–Ю–Ь–Ю–†–°–ђ–Ъ–Ю–У–Ю –Ы–Ж–¶–Х–Ѓ вДЦ3–Я–Њ–і–Њ—А–Њ–ґ –Љ—Ц—Б—В–∞–Љ–Є –£–Ї—А–∞—Ч–љ–Є. –Ы—М–≤—Ц–≤—Б—М–Ї–∞ –Њ–±–ї–∞—Б—В—М
–Я–Њ–і–Њ—А–Њ–ґ –Љ—Ц—Б—В–∞–Љ–Є –£–Ї—А–∞—Ч–љ–Є. –Ы—М–≤—Ц–≤—Б—М–Ї–∞ –Њ–±–ї–∞—Б—В—М–Э–С–£ –і–ї—П –і—Ц—В–µ–є
ћэ
–Ы—М–≤—Ц–≤—Б—М–Ї–∞ –Њ–±–ї–∞—Б—В—М вАУ —Б–њ—А–∞–≤–ґ–љ—П –Ј–љ–∞—Е—Ц–і–Ї–∞ –і–ї—П —В—Г—А–Є—Б—В–∞. –Э–µ –і–∞—А–Љ–∞ —Ч—Ч –љ–∞–Ј–Є–≤–∞—О—В—М –і—Г—И–µ—О —Ц —Б–µ—А—Ж–µ–Љ –£–Ї—А–∞—Ч–љ–Є.–Ј–≤—Ц—В –Ї–µ—А—Ц–≤–љ–Є–Ї–∞ –І–Њ—А–љ–Њ–Љ–Њ—А—Б—М–Ї–Њ–≥–Њ –ї—Ц—Ж–µ—ОвДЦ3 2024.pptx
–Ј–≤—Ц—В –Ї–µ—А—Ц–≤–љ–Є–Ї–∞ –І–Њ—А–љ–Њ–Љ–Њ—А—Б—М–Ї–Њ–≥–Њ –ї—Ц—Ж–µ—ОвДЦ3 2024.pptxssuserb90919
ћэ
–Ј–≤—Ц—В –Ї–µ—А—Ц–≤–љ–Є–Ї–∞ –І–Њ—А–љ–Њ–Љ–Њ—А—Б—М–Ї–Њ–≥–Њ –ї—Ц—Ж–µ—ОвДЦ3 2024.–Т–Њ–ї–Њ–і–Є–Љ–Є—А –Ь–Є–Ї–Њ–ї–∞–є–Њ–≤–Є—З –У–∞–≥–µ–љ–Љ–µ–є—Б—В–µ—А. –Я–Њ–Ї–ї–Є–Ї–∞–љ–љ—П —Е—Г–і–Њ–ґ–љ–Є–Ї–∞
–Т–Њ–ї–Њ–і–Є–Љ–Є—А –Ь–Є–Ї–Њ–ї–∞–є–Њ–≤–Є—З –У–∞–≥–µ–љ–Љ–µ–є—Б—В–µ—А. –Я–Њ–Ї–ї–Є–Ї–∞–љ–љ—П —Е—Г–і–Њ–ґ–љ–Є–Ї–∞–Э–С–£ –і–ї—П –і—Ц—В–µ–є
ћэ
–Т–Є–њ—Г—Б–Ї –Њ–Ј–љ–∞–є–Њ–Љ–Є—В—М —Ц–Ј —В–≤–Њ—А—З—Ц—Б—В—О –Т–Њ–ї–Њ–і–Є–Љ–Є—А–∞ –Ь–Є–Ї–Њ–ї–∞–є–Њ–≤–Є—З–∞ –У–∞–≥–µ–љ–Љ–µ–є—Б—В–µ—А–∞ вАУ —Е—Г–і–Њ–ґ–љ–Є–Ї–∞-–≤–Є–Ї–ї–∞–і–∞—З–∞, –≥—А–∞—Д—Ц–Ї–∞, –Љ–Є—Б—В–µ—Ж—В–≤–Њ–Ј–љ–∞–≤—Ж—П, –Ї–µ—А–∞–Љ—Ц—Б—В–∞, –µ—В–љ–Њ–≥—А–∞—Д–∞, –≤–Є–і–∞–≤—Ж—П.
–С—Ц–ї—М—И–µ —Ц–љ—Д–Њ—А–Љ–∞—Ж—Ц—Ч –љ–∞ —Б–∞–є—В—Ц –Э–∞—Ж—Ц–Њ–љ–∞–ї—М–љ–Њ—Ч –±—Ц–±–ї—Ц–Њ—В–µ–Ї–Є –£–Ї—А–∞—Ч–љ–Є –і–ї—П –і—Ц—В–µ–є: https://chl.kiev.ua/Default.aspx?id=5497–Ч–≤—Ц—В —Б–Њ—Ж—Ц–∞–ї—М–љ–Њ-–њ—Б–Є—Е–Њ–ї–Њ–≥—Ц—З–љ–Њ—Ч —Б–ї—Г–ґ–±–Є 1.pptx
–Ч–≤—Ц—В —Б–Њ—Ж—Ц–∞–ї—М–љ–Њ-–њ—Б–Є—Е–Њ–ї–Њ–≥—Ц—З–љ–Њ—Ч —Б–ї—Г–ґ–±–Є 1.pptxssuserb90919
ћэ
–Ч–≤—Ц—В —Б–Њ—Ж—Ц–∞–ї—М–љ–Њ-–њ—Б–Є—Е–Њ–ї–Њ–≥—Ц—З–љ–Њ—Ч —Б–ї—Г–ґ–±–Є–Я–Њ–і–Њ—А–Њ–ґ –Љ—Ц—Б—В–∞–Љ–Є –£–Ї—А–∞—Ч–љ–Є. –Ы—М–≤—Ц–≤—Б—М–Ї–∞ –Њ–±–ї–∞—Б—В—М
–Я–Њ–і–Њ—А–Њ–ґ –Љ—Ц—Б—В–∞–Љ–Є –£–Ї—А–∞—Ч–љ–Є. –Ы—М–≤—Ц–≤—Б—М–Ї–∞ –Њ–±–ї–∞—Б—В—М–Э–С–£ –і–ї—П –і—Ц—В–µ–є
ћэ
–Т–Њ–ї–Њ–і–Є–Љ–Є—А –Ь–Є–Ї–Њ–ї–∞–є–Њ–≤–Є—З –У–∞–≥–µ–љ–Љ–µ–є—Б—В–µ—А. –Я–Њ–Ї–ї–Є–Ї–∞–љ–љ—П —Е—Г–і–Њ–ґ–љ–Є–Ї–∞
–Т–Њ–ї–Њ–і–Є–Љ–Є—А –Ь–Є–Ї–Њ–ї–∞–є–Њ–≤–Є—З –У–∞–≥–µ–љ–Љ–µ–є—Б—В–µ—А. –Я–Њ–Ї–ї–Є–Ї–∞–љ–љ—П —Е—Г–і–Њ–ґ–љ–Є–Ї–∞–Э–С–£ –і–ї—П –і—Ц—В–µ–є
ћэ
–Ч–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П —Ц–љ—В–µ–≥—А–∞–ї–∞ (11 –Ї–ї–∞—Б)
- 1. –£–†–Ю–Ъ –Р–Ы–У–Х–С–†–Ш ¬Ђ –Ч–Р–°–Ґ–Ю–°–£–Т–Р–Э–Э–ѓ –Ж–Э–Ґ–Х–У–†–Р–Ы–Р ¬ї (11 –Ї–ї–∞—Б –Р–Ї–∞–і–µ–Љ—Ц—З–љ–Є–є —А—Ц–≤–µ–љ—М.)
- 2. 1. –Ч–∞—Б–≤–Њ—Ч—В–Є –њ–Њ–љ—П—В—В—П —Ц–љ—В–µ–≥—А–∞–ї—Г 2–°—Д–Њ—А–Љ—Г–≤–∞–љ–љ—П –≤–Љ—Ц–љ–љ–љ—П —Ц –љ–∞–≤–Є—З–Ї–Є –Ј–∞—Б—В–Њ—Б–Њ–≤—Г–≤–∞—В–Є —Ц–љ—В–µ–≥—А–∞–ї –і–Њ –Њ–±—З–Є—Б–ї–µ–љ–љ—П –њ–ї–Њ—Й –њ–ї–Њ—Б–Ї–Є—Е —Д—Ц–≥—Г—А. 3–§–Њ—А–Љ—Г–≤–∞—В–Є —Ц —А–Њ–Ј–≤–Є–≤–∞—В–Є –≤–Љ—Ц–љ–љ—П –Ј–∞—Б—В–Њ—Б–Њ–≤—Г–≤–∞—В–Є —Ц–љ—В–µ–≥—А–∞–ї –і–ї—П –≤–Є—А—Ц—И–µ–љ–љ—П –Ј–∞–≤–і–∞–љ—М –≤ –≥–µ–Њ–Љ–µ—В—А—Ц—Ч, —Д—Ц–Ј–Є–Ї–Є, –ї–Њ–≥—Ц—З–љ–µ —Ц –∞–±—Б—В—А–∞–Ї—В–љ–µ –Љ–Є—Б–ї–µ–љ–љ—П, –Љ–∞—В–µ–Љ–∞—В–Є—З–љ—Г –Љ–Њ–≤—Г, –љ–∞–≤–Є—З–Ї–Є –Њ—А–≥–∞–љ—Ц–Ј–∞—Ж—Ц–є–љ–Њ—Ч —А–Њ–±–Њ—В–Є –љ–∞ —Г—А–Њ—Ж—Ц, —А–Њ–±–Є—В–Є –≤–Є—Б–љ–Њ–≤–Ї–Є, –≤–µ—Б—В–Є –µ–≤—А–Є—Б—В–Є—З–љ—Г –±–µ—Б—Ц–і—Г. 4. –Т–Є—Е–Њ–≤—Г–≤–∞—В–Є —Г–≤–∞–≥—Г, –≤–Љ—Ц–љ–љ—П –Њ—А–≥–∞–љ—Ц–Ј–Њ–≤—Г–≤–∞—В–Є —Б–≤–Њ—О —А–Њ–±–Њ—В—Г –љ–∞ —Г—А–Њ—Ж—Ц, —Б–∞–Љ–Њ–Њ—Ж—Ц–љ–Ї—Г —Ц —Б–∞–Љ–Њ–Ї–Њ–љ—В—А–Њ–ї—М. 5.–Т–Є—Е–Њ–≤—Г–≤–∞—В–Є –Ї—Г–ї—М—В—Г—А—Г –њ–Њ–±—Г–і–Њ–≤–Є –≥—А–∞—Д—Ц–Ї—Ц–≤ —Д—Г–љ–Ї—Ж—Ц–є.
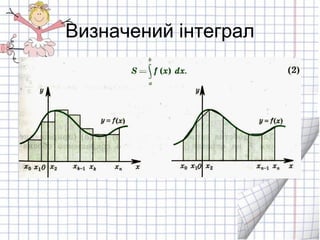
- 3. –Т–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї )a(F)b(F)x(Fdx)x(f b a b a вИТ==вИЂ вАУ —Д–Њ—А–Љ—Г–ї–∞ –Э—М—О—В–Њ–љ–∞-–Ы–µ–є–±–љ—Ц—Ж–∞. –У–µ–Њ–Љ–µ—В—А–Є—З–љ–Є–є –Ј–Љ—Ц—Б—В –≤–Є–Ј–љ–∞—З–µ–љ–Њ–≥–Њ —Ц–љ—В–µ–≥—А–∞–ї–∞ –њ–Њ–ї—П–≥–∞—Ф –≤ —В–Њ–Љ—Г, —Й–Њ –≤–Є–Ј–љ–∞—З–µ–љ–Є–є —Ц–љ—В–µ–≥—А–∞–ї –і–Њ—А—Ц–≤–љ—О—Ф –њ–ї–Њ—Й—Ц –Ї—А–Є–≤–Њ–ї—Ц–љ—Ц–є–љ–Њ—Ч —В—А–∞–њ–µ—Ж—Ц—Ч, —Г—В–≤–Њ—А–µ–љ–Њ—Ч –ї—Ц–љ—Ц—П–Љ–Є: –Ј–≤–µ—А—Е—Г –Њ–±–Љ–µ–ґ–µ–љ–Њ—О –Ї—А–Є–≤–Њ—О —Г = f (—Е), —Ц –њ—А—П–Љ–Є–Љ–Є —Г = 0, —Е = –∞, —Е = b.
- 5. –Ч–љ–∞–є—В–Є –њ–µ—А–≤—Ц—Б–љ—Г: 6 7—Е —Б—Е +7 7 —Е —Б —Е + 8 8 —Е 1 ln x + —Б sin 2x —Бx +вИТ 2cos 2 1
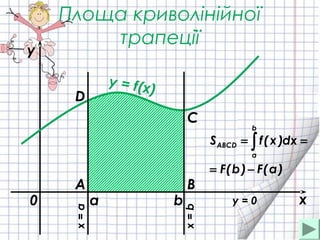
- 8. –Я–ї–Њ—Й–∞ –Ї—А–Є–≤–Њ–ї—Ц–љ—Ц–є–љ–Њ—Ч —В—А–∞–њ–µ—Ж—Ц—Ч a b x y y = f(x) 0 )a(F)b(F dx)x(fS b a ABCD вИТ= == вИЂ A B C D x=a x=b y = 0
- 9. –†–Њ–Ј–≤–†–Њ–Ј–≤вАЩвАЩ—П–Ј—Г—Ф–Љ–Њ —А–∞–Ј–Њ–Љ—П–Ј—Г—Ф–Љ–Њ —А–∞–Ј–Њ–Љ –Ю–±—З–Є—Б–ї–Є—В–Є –њ–ї–Њ—Й—Г —В—А–Є–Ї—Г—В–љ–Є–Ї–∞, –Њ–±–Љ–µ–ґ–µ–љ–Њ–≥–Њ –≤—Ц—Б—Б—О –Ю–•, –њ—А—П–Љ–Є–Љ–Є —Е = 6 —Ц —Г = 2—Е. 60 —Г —Е –£=2—Е
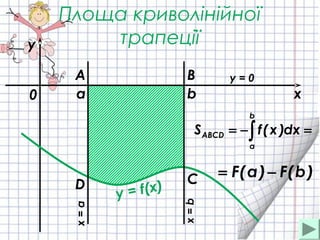
- 10. –Я–ї–Њ—Й–∞ –Ї—А–Є–≤–Њ–ї—Ц–љ—Ц–є–љ–Њ—Ч —В—А–∞–њ–µ—Ж—Ц—Ч a b x y y = f(x) 0 A B CD x=a x=b y = 0 вИЂ =вИТ= b a ABCD dx)x(fS )b(F)a(F вИТ=
- 11. –Ч–∞–≤–і–∞–љ–љ—П –Ф–Я–Р –Ј —В–µ–Љ–Є –Ч–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ
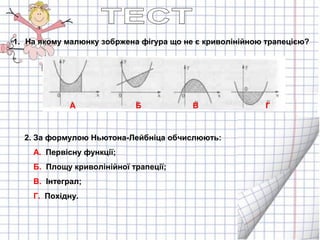
- 12. 1. –Э–∞ —П–Ї–Њ–Љ—Г –Љ–∞–ї—О–љ–Ї—Г –Ј–Њ–±—А–ґ–µ–љ–∞ —Д—Ц–≥—Г—А–∞ —Й–Њ –љ–µ —Ф –Ї—А–Є–≤–Њ–ї—Ц–љ—Ц–є–љ–Њ—О —В—А–∞–њ–µ—Ж—Ц—Ф—О? 2. –Ч–∞ —Д–Њ—А–Љ—Г–ї–Њ—О –Э—М—О—В–Њ–љ–∞-–Ы–µ–є–±–љ—Ц—Ж–∞ –Њ–±—З–Є—Б–ї—О—О—В—М: –Р. –Я–µ—А–≤—Ц—Б–љ—Г —Д—Г–љ–Ї—Ж—Ц—Ч; –С. –Я–ї–Њ—Й—Г –Ї—А–Є–≤–Њ–ї—Ц–љ—Ц–є–љ–Њ—Ч —В—А–∞–њ–µ—Ж—Ц—Ч; –Т. –Ж–љ—В–µ–≥—А–∞–ї; –У. –Я–Њ—Е—Ц–і–љ—Г. –Р –С –Т –У
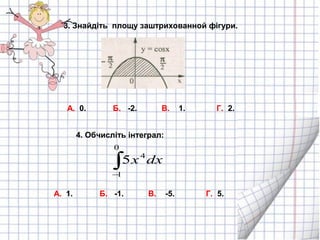
- 13. 3. –Ч–љ–∞–є–і—Ц—В—М –њ–ї–Њ—Й—Г –Ј–∞—И—В—А–Є—Е–Њ–≤–∞–љ–љ–Њ–є —Д—Ц–≥—Г—А–Є. –Р. 1. –С. -1. –Т. -5. –У. 5. 4. –Ю–±—З–Є—Б–ї—Ц—В—М —Ц–љ—В–µ–≥—А–∞–ї: вИЂвИТ 0 1 4 5 dx—Е –Р. 0. –С. -2. –Т. 1. –У. 2.
- 14. –Р. 2a. –С. 2cos a. –Т. 0. –У. 2. 5. –Ю–±—З–Є—Б–ї—Ц—В—М —Ц–љ—В–µ–≥—А–∞–ї: вИЂвИТ a a —Еdxsin вИЂ 1 0 3 3 dx–µ —Е –Р. . –С. . –Т. . –У. .33 3 вИТ–µ 13 вИТ–µ 3 33 –µ+ 3 1 –µвИТ
- 15. –Я–µ—А–µ–≤—Ц—А—М —Б–µ–±–µ 1 –С 2 –С 3 –У 4 –С 5 –Т 6 –С
- 16. 1.–ѓ–Ї –Њ–±—З–Є—Б–ї—О—Ф—В—М—Б—П –њ–ї–Њ—Й–∞ –Ї—А–Є–≤–Њ–ї—Ц–љ—Ц–є–љ–Њ—Ч —В—А–∞–њ–µ—Ж—Ц—Ч? 2.–§–Њ—А–Љ—Г–ї–∞ –Э—М—О—В–Њ–љ–∞ - –Ы–µ–є–±–љ—Ц—Ж–∞ 3.–ѓ–Ї –Ј–∞—Б—В–Њ—Б–Њ–≤—Г—Ф—В—М—Б—П —Ц–љ—В–µ–≥—А–∞–ї –≤ —Д—Ц–Ј–Є—Ж—Ц? a b y= f (x)
