Έ†œ¹ΈΩœÉΈΩΈΦΈΩΈ·œâœÉΈΖ 2019 Έ±œÄœ¨ œ³ΈΩ ΈöΈ±ΈΜΈ±ΈΦΈ±œ¹Έ·
- 1. ΈëΈΓΈßΈ½ 1Έ½ΈΘ ΈΘΈïΈ¦ΈôΈîΈëΈΘ ΈïΈûΈïΈΛΈëΈΘΈïΈôΈΘ Έ†ΈΓΈüΈΘΈüΈ€ΈüΈôΈ©ΈΘΈ½ΈΘ Έ™' ΈΛΈëΈûΈ½ΈΘ Έ™ΈïΈùΈôΈöΈüΈΞ Έ¦ΈΞΈöΈïΈôΈüΈΞ ΈïΈ¦Έ¦Έ½ΈùΈüΈ™ΈëΈ¦Έ¦ΈôΈöΈ½ΈΘ ΈΘΈßΈüΈ¦Έ½ΈΘ ΈöΈëΈ¦ΈëΈ€ΈëΈΓΈô ΈΛΈïΈΛΈëΈΓΈΛΈ½ 9 ΈôΈëΈùΈüΈΞΈëΈΓΈôΈüΈΞ 2019 ΈïΈûΈïΈΛΈëΈ•ΈüΈ€ΈïΈùΈü Έ€ΈëΈ‰Έ½Έ€Έë:Έ€ΈëΈ‰Έ½Έ€ΈëΈΛΈôΈöΈë ΈüΈ€ΈëΈîΈëΈΘ Έ†ΈΓΈüΈΘΈëΈùΈëΈΛΈüΈ¦ΈôΈΘΈ€ΈüΈΞ Έ‰ΈïΈΛΈôΈöΈ©Έù ΈΘΈ†ΈüΈΞΈîΈ©Έù-ΈüΈôΈöΈüΈùΈüΈ€ΈôΈëΈΘ & Έ†Έ¦Έ½ΈΓΈüΈΠΈüΈΓΈôΈöΈ½ΈΘ ΈΘΈΞΈùΈüΈ¦Έü ΈΘΈïΈ¦ΈôΈîΈ©Έù: Έ†ΈïΈùΈΛΈï (5) Έ‰ΈïΈ€Έë Έë Έë1. ΈùΈ± Έ±œÄΈΩΈ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ Έ±ΈΫ ΈΩΈΙ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒΈΙœ² f,g ΈΒΈ·ΈΫΈ±ΈΙ œÄΈ±œ¹Έ±Έ≥œâΈ≥Έ·œÉΈΙΈΦΈΒœ² œÉœ³ΈΩ 0x , œ³œ¨œ³ΈΒ ΈΖ œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖ f gοÄΪ ΈΒΈ·ΈΫΈ±ΈΙ œÄΈ±œ¹Έ±Έ≥œâΈ≥Έ·œÉΈΙΈΦΈΖ œÉœ³ΈΩ 0x ΈΚΈ±ΈΙ ΈΙœÉœ΅œçΈΒΈΙ οÄ® οÄ© οÄ® οÄ© οÄ® οÄ© οÄ® οÄ©0 0 0f g x f x g xο²Δ ο²Δ ο²ΔοÄΪ οÄΫ οÄΪ . Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 7 Έë2. Έ‰ΈΒœâœ¹Έ°œÉœ³ΈΒ œ³ΈΖΈΫ œÄΈ±œ¹Έ±ΈΚΈ§œ³œâ œÄœ¹œ¨œ³Έ±œÉΈΖ: ¬Ϊ Έ½ œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖ οÄ® οÄ© ο¹¦ οÄ©f x x , x 0,οÄΫ οÉé οÄΪο²Ξ ΈΒΈ·ΈΫΈ±ΈΙ œÄΈ±œ¹Έ±Έ≥œâΈ≥Έ·œÉΈΙΈΦΈΖ œÉœ³ΈΩ ο¹¦ οÄ©0,οÄΪο²Ξ ΈΚΈ±ΈΙ ΈΙœÉœ΅œçΈΒΈΙ οÄ® οÄ© 1 x 2 x ο²Δ οÄΫ . Έ±. ΈùΈ± œ΅Έ±œ¹Έ±ΈΚœ³ΈΖœ¹Έ·œÉΈΒœ³ΈΒ œ³ΈΖΈΫ œÄΈ±œ¹Έ±œÄΈ§ΈΫœâ œÄœ¹œ¨œ³Έ±œÉΈΖ Έ≥œ¹Έ§œÜΈΩΈΫœ³Έ±œ² œÉœ³ΈΩ œ³ΈΒœ³œ¹Έ§Έ¥ΈΙœ¨ œÉΈ±œ², œ³ΈΩ Έ≥œ¹Έ§ΈΦΈΦΈ± Έë , Έ±ΈΫ ΈΒΈ·ΈΫΈ±ΈΙ Έ±ΈΜΈΖΈΗΈ°œ², Έ° œ³ΈΩ Έ≥œ¹Έ§ΈΦΈΦΈ± Έ® , Έ±ΈΫ ΈΒΈ·ΈΫΈ±ΈΙ œàΈΒœÖΈ¥Έ°œ². Έ€ΈΩΈΫΈ§Έ¥Έ± 1 Έ≤. ΈùΈ± Έ±ΈΙœ³ΈΙΈΩΈΜΈΩΈ≥Έ°œÉΈΒœ³ΈΒ œ³ΈΖΈΫ Έ±œÄΈ§ΈΫœ³ΈΖœÉΈ° œÉΈ±œ² œÉœ³ΈΩ ΈΒœ¹œéœ³ΈΖΈΦΈ± (Έ±). Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 4 Έë3. ΈΘœ³ΈΩΈΫ œÄΈ±œ¹Έ±ΈΚΈ§œ³œâ œÄΈ·ΈΫΈ±ΈΚΈ± Έ¥Έ·ΈΫΈΩΈΫœ³Έ±ΈΙ ΈΩΈΙ Έ≥œ¹Έ±œÜΈΙΈΚΈ≠œ² œÄΈ±œ¹Έ±œÉœ³Έ§œÉΈΒΈΙœ² œ³œ¹ΈΙœéΈΫ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒœâΈΫ œÉœ³ΈΖΈΫ œÄœ¹œéœ³ΈΖ Έ≥œ¹Έ±ΈΦΈΦΈ° ΈΚΈ±ΈΙ œ³œâΈΫ Έ±ΈΫœ³Έ·œÉœ³œ¹ΈΩœÜœéΈΫ œ³ΈΩœÖœ² œÉœ³ΈΖΈΫ Έ¥ΈΒœçœ³ΈΒœ¹ΈΖ Έ≥œ¹Έ±ΈΦΈΦΈ°. ΈùΈ± Έ≥œ¹Έ§œàΈΒœ³ΈΒ œÉœ³ΈΩ œ³ΈΒœ³œ¹Έ§Έ¥ΈΙœ¨ œÉΈ±œ² œ³ΈΖΈΫ Έ±ΈΫœ³ΈΙœÉœ³ΈΩΈ·œ΅ΈΙœÉΈΖ ΈΚΈ§ΈΗΈΒ œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖœ² ΈΦΈΒ œ³ΈΖΈΫ Έ±ΈΫœ³Έ·œÉœ³œ¹ΈΩœÜΈ° œ³ΈΖœ² ΈΛΈïΈ¦ΈüΈΘ 1Έ½ΈΘ ΈëΈ†Έü 5 ΈΘΈïΈ¦ΈôΈîΈïΈΘ 10.01.2019 ΈëœÄΈΩΈΚΈΜΈΒΈΙœÉœ³ΈΙΈΚΈ§ œÉœ³ΈΩ lisari.blogspot.gr Page 1 of 5
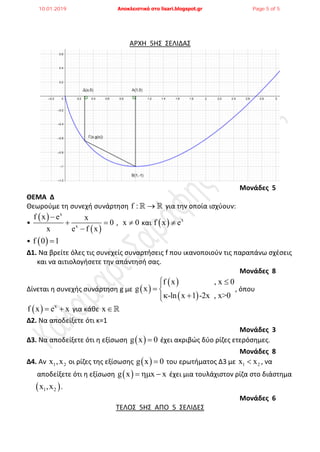
- 2. ΈëΈΓΈßΈ½ 2Έ½ΈΘ ΈΘΈïΈ¦ΈôΈîΈëΈΘ 1. 2. 3. i. ii. iii. Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 3 Έë4. ΈùΈ± œ΅Έ±œ¹Έ±ΈΚœ³ΈΖœ¹Έ·œÉΈΒœ³ΈΒ œ³ΈΙœ² œÄœ¹ΈΩœ³Έ§œÉΈΒΈΙœ² œÄΈΩœÖ Έ±ΈΚΈΩΈΜΈΩœÖΈΗΈΩœçΈΫ, Έ≥œ¹Έ§œÜΈΩΈΫœ³Έ±œ² œÉœ³ΈΩ œ³ΈΒœ³œ¹Έ§Έ¥ΈΙœ¨ œÉΈ±œ²,Έ¥Έ·œÄΈΜΈ± œÉœ³ΈΩ Έ≥œ¹Έ§ΈΦΈΦΈ± œÄΈΩœÖ Έ±ΈΫœ³ΈΙœÉœ³ΈΩΈΙœ΅ΈΒΈ· œÉΈΒ ΈΚΈ§ΈΗΈΒ œÄœ¹œ¨œ³Έ±œÉΈΖ,œ³ΈΖ ΈΜΈ≠ΈΨΈΖ ΈΘœâœÉœ³œ¨ ,Έ±ΈΫ ΈΖ œÄœ¹œ¨œ³Έ±œÉΈΖ ΈΒΈ·ΈΫΈ±ΈΙ œÉœâœÉœ³Έ°,Έ° Έ¦Έ§ΈΗΈΩœ² ,Έ±ΈΫ ΈΖ œÄœ¹œ¨œ³Έ±œÉΈΖ ΈΒΈ·ΈΫΈ±ΈΙ ΈΜΈ±ΈΫΈΗΈ±œÉΈΦΈ≠ΈΫΈΖ. Έ±. ΈëΈΫ œÖœÄΈ§œ¹œ΅ΈΩœÖΈΫ œ³ΈΙΈΦΈ≠œ² œ³ΈΖœ² œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖœ² f œÄΈΩœÖ Έ±ΈΫΈ°ΈΚΈΩœÖΈΫ œÉœ³ΈΩ œÄΈΒΈ¥Έ·ΈΩ ΈΩœ¹ΈΙœÉΈΦΈΩœç œ³ΈΖœ² œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖœ² g œ³œ¨œ³ΈΒ ΈΩœ¹Έ·ΈΕΈΒœ³Έ±ΈΙ ΈΖ œÉœçΈΫΈΗΈΒœÉΈΖ œ³ΈΖœ² f ΈΦΈΒ œ³ΈΖΈΫ g. Έ≤. ΈëΈΫ ΈΙœÉœ΅œçΈΒΈΙ οÄ® οÄ© οÄ® οÄ©0f x f xο²≥ Έ≥ΈΙΈ± ΈΚΈ§ΈΗΈΒ fx DοÉé œ³œ¨œ³ΈΒ œ³ΈΩ οÄ® οÄ©0f x ΈΒΈ·ΈΫΈ±ΈΙ ΈΖ ΈΒΈΜΈ§œ΅ΈΙœÉœ³ΈΖ œ³ΈΙΈΦΈ° œ³ΈΖœ² f. Έ≥. ΈëΈΫ ΈΩΈΙ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒΈΙœ² f,g Έ≠œ΅ΈΩœÖΈΫ œ¨œ¹ΈΙΈΩ œÉœ³ΈΩ 0x ΈΚΈ±ΈΙ ΈΙœÉœ΅œçΈΒΈΙ οÄ® οÄ© οÄ® οÄ©f x g xο²Θ ΈΚΈΩΈΫœ³Έ§ œÉœ³ΈΩ 0x œ³œ¨œ³ΈΒ ΈΦœÄΈΩœ¹ΈΒΈ· οÄ® οÄ© οÄ® οÄ© 0 0x x x x lim f x = lim g x ο²° ο²° . Έ¥. ΈëΈΫ ΈΦΈΙΈ± œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖ f ΈΒΈ·ΈΫΈ±ΈΙ œÉœÖΈΫΈΒœ΅Έ°œ² œÉœ³ΈΩ ο¹¦ ο¹ù,ο¹Γ ο¹Δ ΈΚΈ±ΈΙ œÖœÄΈ§œ¹œ΅ΈΒΈΙ οÄ® οÄ© οÄ® οÄ©0 0x , : f x 0οÉé ο¹Γ ο¹Δ οÄΫ œ³œ¨œ³ΈΒ οÄ® οÄ© οÄ® οÄ©f f 0ο¹Γ οɽ ο¹Δ οÄΦ . ΈΛΈïΈ¦ΈüΈΘ 2Έ½ΈΘ ΈëΈ†Έü 5 ΈΘΈïΈ¦ΈôΈîΈïΈΘ 10.01.2019 ΈëœÄΈΩΈΚΈΜΈΒΈΙœÉœ³ΈΙΈΚΈ§ œÉœ³ΈΩ lisari.blogspot.gr Page 2 of 5
- 3. ΈëΈΓΈßΈ½ 3Έ½ΈΘ ΈΘΈïΈ¦ΈôΈîΈëΈΘ ΈΒ. ΈëΈΫ ΈΦΈΙΈ± œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖ f Έ¥ΈΒΈΫ ΈΒΈ·ΈΫΈ±ΈΙ œÉœÖΈΫΈΒœ΅Έ°œ² œÉœ³ΈΩ Έ¥ΈΙΈ§œÉœ³ΈΖΈΦΈ± [Έ±, Έ≤] œ³œ¨œ³ΈΒ Έ¥ΈΒΈΫ œÄΈ±Έ·œ¹ΈΫΈΒΈΙ œÖœÄΈΩœ΅œ¹ΈΒœâœ³ΈΙΈΚΈ§ œ¨ΈΜΈΒœ² œ³ΈΙœ² ΈΒΈΫΈ¥ΈΙΈ§ΈΦΈΒœÉΈΒœ² œ³ΈΙΈΦΈ≠œ² ΈΦΈΒœ³Έ±ΈΨœç œ³œâΈΫ οÄ® οÄ©f ο¹Γ ΈΚΈ±ΈΙ οÄ® οÄ©f ο¹Δ . MoΈΫΈ§Έ¥ΈΒœ² 10 Έ‰ΈïΈ€Έë Έ£ ΈΘœ³Έ± œÄΈ±œ¹Έ±ΈΚΈ§œ³œâ œÉœ΅Έ°ΈΦΈ±œ³Έ± Έ¥Έ·ΈΫΈΩΈΫœ³Έ±ΈΙ ΈΩΈΙ Έ≥œ¹Έ±œÜΈΙΈΚΈ≠œ² œÄΈ±œ¹Έ±œÉœ³Έ§œÉΈΒΈΙœ² œ³œâΈΫ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒœâΈΫ f,g. i. ΈùΈ± ΈΒΈΨΈΒœ³Έ§œÉΈΒœ³ΈΒ Έ±ΈΫ ΈΩΈΙ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒΈΙœ² f,g ΈΒΈ·ΈΫΈ±ΈΙ Έ·œÉΈΒœ². ΈùΈ± Έ±ΈΙœ³ΈΙΈΩΈΜΈΩΈ≥Έ°œÉΈΒœ³ΈΒ œ³ΈΖΈΫ Έ±œÄΈ§ΈΫœ³ΈΖœÉΈ° œÉΈ±œ². Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 2 ii. ΈùΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ œ³Έ± œÉΈΖΈΦΈΒΈ·Έ± œÉœ³Έ± ΈΩœÄΈΩΈ·Έ± ΈΩΈΙ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒΈΙœ² f,g Έ¥ΈΒΈΫ ΈΒΈ·ΈΫΈ±ΈΙ œÉœÖΈΫΈΒœ΅ΈΒΈ·œ² œÉœ³Έ± œÄΈΒΈ¥Έ·Έ± ΈΩœ¹ΈΙœÉΈΦΈΩœç œ³ΈΩœÖœ². ΈùΈ± Έ±ΈΙœ³ΈΙΈΩΈΜΈΩΈ≥Έ°œÉΈΒœ³ΈΒ œ³ΈΖΈΫ Έ±œÄΈ§ΈΫœ³ΈΖœÉΈ° œÉΈ±œ². Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 4 iii. ΈùΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ, Έ±ΈΫ œÖœÄΈ§œ¹œ΅ΈΩœÖΈΫ, œ³Έ± œÄΈ±œ¹Έ±ΈΚΈ§œ³œâ œ¨œ¹ΈΙΈ±. Έ±) οÄ® οÄ©x 1 1 lim g xο²° Έ≤) οÄ® οÄ©οÄ® οÄ©x 2 limg f x ο²° Έ≥) οÄ® οÄ© οÄ® οÄ©x 2 f x lim g xο²°οÄ≠ Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 6 iv. ΈùΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ œ³ΈΩ œÄΈΒΈ¥Έ·ΈΩ ΈΩœ¹ΈΙœÉΈΦΈΩœç œ³ΈΖœ² œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖœ² οÄ® οÄ© οÄ® οÄ©οÄ® οÄ©h x f g xοÄΫ οÄΪ . Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 3 ΈΛΈïΈ¦ΈüΈΘ 3Έ½ΈΘ ΈëΈ†Έü 5 ΈΘΈïΈ¦ΈôΈîΈïΈΘ 10.01.2019 ΈëœÄΈΩΈΚΈΜΈΒΈΙœÉœ³ΈΙΈΚΈ§ œÉœ³ΈΩ lisari.blogspot.gr Page 3 of 5
- 4. ΈëΈΓΈßΈ½ 4Έ½ΈΘ ΈΘΈïΈ¦ΈôΈîΈëΈΘ v. ΈùΈ± Έ±œÄΈΩΈ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ œÖœÄΈ§œ¹œ΅ΈΒΈΙ Έ≠ΈΫΈ± œ³ΈΩœÖΈΜΈ§œ΅ΈΙœÉœ³ΈΩΈΫ οÄ® οÄ©0x 1,0οÉé οÄ≠ œ³Έ≠œ³ΈΩΈΙΈΩ œéœÉœ³ΈΒ οÄ® οÄ©0h x 1οÄΫ . Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 5 vi. ΈùΈ± Έ±œÄΈΩΈ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ œÖœÄΈ§œ¹œ΅ΈΒΈΙ Έ≠ΈΫΈ± œ³ΈΩœÖΈΜΈ§œ΅ΈΙœÉœ³ΈΩΈΫ ο¹¦ ο¹ù3,0ο¹ΗοÉé οÄ≠ œ³Έ≠œ³ΈΩΈΙΈΩ œéœÉœ³ΈΒ οÄ® οÄ© 5 3 1 g 2g 3g 2 2 3 g 6 οÉΠ οÉΕ οÉΠ οÉΕ οÉΠ οÉΕ οÄ≠ οÄΪ οÄ≠ οÄΪ οÄ≠οÉß οÉΖ οÉß οÉΖ οÉß οÉΖ οÉ® οÉΗ οÉ® οÉΗ οÉ® οÉΗο¹Η οÄΫ Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 5 Έ‰ΈïΈ€Έë Έ™ ΈîΈ·ΈΫΈΩΈΫœ³Έ±ΈΙ ΈΩΈΙ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒΈΙœ² f : ο²° ΈΚΈ±ΈΙ οÄ® οÄ©g: 0,οÄΪο²Ξ ο²° ΈΦΈΒ οÄ® οÄ©g x xln x xοÄΫ οÄ≠ . Έ½ f ΈΒΈ·ΈΫΈ±ΈΙ œÄΈ±œ¹Έ±Έ≥œâΈ≥Έ·œÉΈΙΈΦΈΖ œÉœ³ΈΩ œ³Έ≠œ³ΈΩΈΙΈ± œéœÉœ³ΈΒ οÄ® οÄ©f ln x x ln xο²Δ οÄΫ οɽ Έ≥ΈΙΈ± ΈΚΈ§ΈΗΈΒ οÄ® οÄ©x 0,οÉé οÄΪο²Ξ . ΈïœÄΈ·œÉΈΖœ² Έ¥Έ·ΈΫΈΒœ³Έ±ΈΙ ΈΖ ΈΒœÖΈΗΈΒΈ·Έ± (ΈΒ) ΈΦΈΒ ΈΒΈΨΈ·œÉœâœÉΈΖ : y x eο¹Ξ οÄΫ οÄ≠ . Έ™1. ΈùΈ± Έ±œÄΈΩΈ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ ΈΖ ΈΒœÖΈΗΈΒΈ·Έ± (ΈΒ) ΈΒœÜΈ§œÄœ³ΈΒœ³Έ±ΈΙ œÉœ³ΈΖ Έ≥œ¹Έ±œÜΈΙΈΚΈ° œÄΈ±œ¹Έ§œÉœ³Έ±œÉΈΖ œ³ΈΖœ² œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖœ² g. Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 5 Έ™2. ΈùΈ± Έ±œÄΈΩΈ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ ΈΩ œ³œçœÄΈΩœ² œ³ΈΖœ² fο²Δ Έ≥ΈΙΈ± ΈΚΈ§ΈΗΈΒ xοÉé ΈΒΈ·ΈΫΈ±ΈΙ οÄ® οÄ© x f x xeο²Δ οÄΫ Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 5 Έ™3. ΈùΈ± Έ±œÄΈΩΈ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ œÖœÄΈ§œ¹œ΅ΈΒΈΙ Έ≠ΈΫΈ± œ³ΈΩœÖΈΜΈ§œ΅ΈΙœÉœ³ΈΩΈΫ οÄ® οÄ©0,1ο¹ΗοÉé œ³Έ≠œ³ΈΩΈΙΈΩ œéœÉœ³ΈΒ ΈΖ ΈΒœÜΈ±œÄœ³ΈΩΈΦΈ≠ΈΫΈΖ œ³ΈΖœ² fC œÉœ³ΈΩ œÉΈΖΈΦΈΒΈ·ΈΩ οÄ® οÄ©οÄ® οÄ©,fο¹Η ο¹Η ΈΫΈ± ΈΒΈ·ΈΫΈ±ΈΙ œÄΈ±œ¹Έ§ΈΜΈΜΈΖΈΜΈΖ œÉœ³ΈΖΈΫ ΈΒœÖΈΗΈΒΈ·Έ± (ΈΒ). Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 6 Έ™4. ΈùΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ œ³ΈΖΈΫ ΈΒΈΨΈ·œÉœâœÉΈΖ œ³ΈΖœ² ΈΒœÜΈ±œÄœ³ΈΩΈΦΈ≠ΈΫΈΖœ² œ³ΈΖœ² Έ≥œ¹Έ±œÜΈΙΈΚΈ°œ² œÄΈ±œ¹Έ§œÉœ³Έ±œÉΈΖœ² œ³ΈΖœ² fο²Δ œÉœ³ΈΩ 0x 0οÄΫ Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 4 Έ™5. ΈïΈ≥Έ≥œ¹Έ§œÜΈΩœÖΈΦΈΒ œ³ΈΩ œ³œ¹Έ±œÄΈ≠ΈΕΈΙΈΩ ΈëΈ£Έ™Έî ΈΦΈΒœ³Έ±ΈΨœç œ³ΈΖœ² Έ≥œ¹Έ±œÜΈΙΈΚΈ°œ² œÄΈ±œ¹Έ§œÉœ³Έ±œÉΈΖœ² œ³ΈΖœ² g ΈΚΈ±ΈΙ œ³ΈΩœÖ Έ§ΈΨΈΩΈΫΈ± xΈ³x œ¨œÄœâœ² œÜΈ±Έ·ΈΫΈΒœ³Έ±ΈΙ œÉœ³ΈΩ œÄΈ±œ¹Έ±ΈΚΈ§œ³œâ œÉœ΅Έ°ΈΦΈ±. ΈüΈΙ ΈΚΈΩœ¹œÖœÜΈ≠œ² œ³ΈΩœÖ œ³œ¹Έ±œÄΈΒΈΕΈ·ΈΩœÖ Έ≠œ΅ΈΩœÖΈΫ œÉœÖΈΫœ³ΈΒœ³Έ±Έ≥ΈΦΈ≠ΈΫΈΒœ² Έë(1,0), Έ£(1,-1), Έ™(x,g(x)), Έî(x,0). ΈùΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ œ³ΈΖ œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖ œ³ΈΩœÖ ΈΒΈΦΈ≤Έ±Έ¥ΈΩœç œ³ΈΩœÖ œ³œ¹Έ±œÄΈΒΈΕΈ·ΈΩœÖ (ΈëΈ£Έ™Έî)=Έï œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒΈΙ œ³ΈΩœÖ x ΈΚΈ±ΈΙ œ³ΈΖΈΫ œÄΈ±œ¹Έ§Έ≥œâΈ≥œ¨ œ³ΈΩœÖ. ΈΛΈïΈ¦ΈüΈΘ 4Έ½ΈΘ ΈëΈ†Έü 5 ΈΘΈïΈ¦ΈôΈîΈïiΈΘ 10.01.2019 ΈëœÄΈΩΈΚΈΜΈΒΈΙœÉœ³ΈΙΈΚΈ§ œÉœ³ΈΩ lisari.blogspot.gr Page 4 of 5
- 5. ΈëΈΓΈßΈ½ 5Έ½ΈΘ ΈΘΈïΈ¦ΈôΈîΈëΈΘ Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 5 Έ‰ΈïΈ€Έë Έî Έ‰ΈΒœâœ¹ΈΩœçΈΦΈΒ œ³ΈΖ œÉœÖΈΫΈΒœ΅Έ° œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖ f : ο²° Έ≥ΈΙΈ± œ³ΈΖΈΫ ΈΩœÄΈΩΈ·Έ± ΈΙœÉœ΅œçΈΩœÖΈΫ: βÄΔ οÄ® οÄ© οÄ® οÄ© x x f x e x 0 x e f x οÄ≠ οÄΪ οÄΫ οÄ≠ , x 0ο²Ι ΈΚΈ±ΈΙ οÄ® οÄ© x f x eο²Ι βÄΔ οÄ® οÄ©f 0 1οÄΫ Έî1. ΈùΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ œ¨ΈΜΈΒœ² œ³ΈΙœ² œÉœÖΈΫΈΒœ΅ΈΒΈ·œ² œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒΈΙœ² f œÄΈΩœÖ ΈΙΈΚΈ±ΈΫΈΩœÄΈΩΈΙΈΩœçΈΫ œ³ΈΙœ² œÄΈ±œ¹Έ±œÄΈ§ΈΫœâ œÉœ΅Έ≠œÉΈΒΈΙœ² ΈΚΈ±ΈΙ ΈΫΈ± Έ±ΈΙœ³ΈΙΈΩΈΜΈΩΈ≥Έ°œÉΈΒœ³ΈΒ œ³ΈΖΈΫ Έ±œÄΈ§ΈΫœ³ΈΖœÉΈ° œÉΈ±œ². Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 8 ΈîΈ·ΈΫΈΒœ³Έ±ΈΙ ΈΖ œÉœÖΈΫΈΒœ΅Έ°œ² œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖ g ΈΦΈΒ οÄ® οÄ© οÄ® οÄ© οÄ® οÄ© f x , x 0 g x -ln x 1 -2x , x>0 οɧ ο²ΘοÉ· οÄΫ οÉ≠ ο¹Ϊ οÄΪοÉ·οÉ° , œ¨œÄΈΩœÖ οÄ® οÄ© x f x e xοÄΫ οÄΪ Έ≥ΈΙΈ± ΈΚΈ§ΈΗΈΒ xοÉé Έî2. ΈùΈ± Έ±œÄΈΩΈ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ ΈΚ=1 Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 3 Έî3. ΈùΈ± Έ±œÄΈΩΈ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ ΈΖ ΈΒΈΨΈ·œÉœâœÉΈΖ οÄ® οÄ©g x 0οÄΫ Έ≠œ΅ΈΒΈΙ Έ±ΈΚœ¹ΈΙΈ≤œéœ² Έ¥œçΈΩ œ¹Έ·ΈΕΈΒœ² ΈΒœ³ΈΒœ¹œ¨œÉΈΖΈΦΈΒœ². Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 8 Έî4. ΈëΈΫ 1 2x ,x ΈΩΈΙ œ¹Έ·ΈΕΈΒœ² œ³ΈΖœ² ΈΒΈΨΈ·œÉœâœÉΈΖœ² οÄ® οÄ©g x 0οÄΫ œ³ΈΩœÖ ΈΒœ¹œâœ³Έ°ΈΦΈ±œ³ΈΩœ² Έî3 ΈΦΈΒ 1 2x xοÄΦ , ΈΫΈ± Έ±œÄΈΩΈ¥ΈΒΈ·ΈΨΈΒœ³ΈΒ œ¨œ³ΈΙ ΈΖ ΈΒΈΨΈ·œÉœâœÉΈΖ οÄ® οÄ©g x x xοÄΫ ο¹®ο¹≠ οÄ≠ Έ≠œ΅ΈΒΈΙ ΈΦΈΙΈ± œ³ΈΩœÖΈΜΈ§œ΅ΈΙœÉœ³ΈΩΈΫ œ¹Έ·ΈΕΈ± œÉœ³ΈΩ Έ¥ΈΙΈ§œÉœ³ΈΖΈΦΈ± οÄ® οÄ©1 2x ,x . Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 6 ΈΛΈïΈ¦ΈüΈΘ 5Έ½ΈΘ ΈëΈ†Έü 5 ΈΘΈïΈ¦ΈôΈîΈïΈΘ 10.01.2019 ΈëœÄΈΩΈΚΈΜΈΒΈΙœÉœ³ΈΙΈΚΈ§ œÉœ³ΈΩ lisari.blogspot.gr Page 5 of 5


![ΈëΈΓΈßΈ½ 3Έ½ΈΘ ΈΘΈïΈ¦ΈôΈîΈëΈΘ
ΈΒ. ΈëΈΫ ΈΦΈΙΈ± œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖ f Έ¥ΈΒΈΫ ΈΒΈ·ΈΫΈ±ΈΙ œÉœÖΈΫΈΒœ΅Έ°œ² œÉœ³ΈΩ Έ¥ΈΙΈ§œÉœ³ΈΖΈΦΈ± [Έ±, Έ≤] œ³œ¨œ³ΈΒ Έ¥ΈΒΈΫ œÄΈ±Έ·œ¹ΈΫΈΒΈΙ
œÖœÄΈΩœ΅œ¹ΈΒœâœ³ΈΙΈΚΈ§ œ¨ΈΜΈΒœ² œ³ΈΙœ² ΈΒΈΫΈ¥ΈΙΈ§ΈΦΈΒœÉΈΒœ² œ³ΈΙΈΦΈ≠œ² ΈΦΈΒœ³Έ±ΈΨœç œ³œâΈΫ οÄ® οÄ©f ο¹Γ ΈΚΈ±ΈΙ οÄ® οÄ©f ο¹Δ .
MoΈΫΈ§Έ¥ΈΒœ² 10
Έ‰ΈïΈ€Έë Έ£
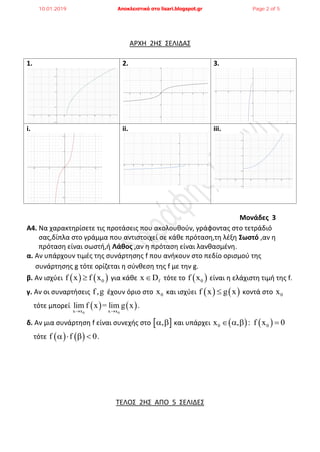
ΈΘœ³Έ± œÄΈ±œ¹Έ±ΈΚΈ§œ³œâ œÉœ΅Έ°ΈΦΈ±œ³Έ± Έ¥Έ·ΈΫΈΩΈΫœ³Έ±ΈΙ ΈΩΈΙ Έ≥œ¹Έ±œÜΈΙΈΚΈ≠œ² œÄΈ±œ¹Έ±œÉœ³Έ§œÉΈΒΈΙœ² œ³œâΈΫ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒœâΈΫ f,g.
i. ΈùΈ± ΈΒΈΨΈΒœ³Έ§œÉΈΒœ³ΈΒ Έ±ΈΫ ΈΩΈΙ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒΈΙœ² f,g ΈΒΈ·ΈΫΈ±ΈΙ Έ·œÉΈΒœ². ΈùΈ± Έ±ΈΙœ³ΈΙΈΩΈΜΈΩΈ≥Έ°œÉΈΒœ³ΈΒ œ³ΈΖΈΫ Έ±œÄΈ§ΈΫœ³ΈΖœÉΈ° œÉΈ±œ².
Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 2
ii. ΈùΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ œ³Έ± œÉΈΖΈΦΈΒΈ·Έ± œÉœ³Έ± ΈΩœÄΈΩΈ·Έ± ΈΩΈΙ œÉœÖΈΫΈ±œ¹œ³Έ°œÉΈΒΈΙœ² f,g Έ¥ΈΒΈΫ ΈΒΈ·ΈΫΈ±ΈΙ œÉœÖΈΫΈΒœ΅ΈΒΈ·œ² œÉœ³Έ± œÄΈΒΈ¥Έ·Έ±
ΈΩœ¹ΈΙœÉΈΦΈΩœç œ³ΈΩœÖœ². ΈùΈ± Έ±ΈΙœ³ΈΙΈΩΈΜΈΩΈ≥Έ°œÉΈΒœ³ΈΒ œ³ΈΖΈΫ Έ±œÄΈ§ΈΫœ³ΈΖœÉΈ° œÉΈ±œ².
Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 4
iii. ΈùΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ, Έ±ΈΫ œÖœÄΈ§œ¹œ΅ΈΩœÖΈΫ, œ³Έ± œÄΈ±œ¹Έ±ΈΚΈ§œ³œâ œ¨œ¹ΈΙΈ±.
Έ±)
οÄ® οÄ©x 1
1
lim
g xο²°
Έ≤) οÄ® οÄ©οÄ® οÄ©x 2
limg f x
ο²°
Έ≥)
οÄ® οÄ©
οÄ® οÄ©x 2
f x
lim
g xο²°οÄ≠
Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 6
iv. ΈùΈ± Έ≤œ¹ΈΒΈ·œ³ΈΒ œ³ΈΩ œÄΈΒΈ¥Έ·ΈΩ ΈΩœ¹ΈΙœÉΈΦΈΩœç œ³ΈΖœ² œÉœÖΈΫΈ§œ¹œ³ΈΖœÉΈΖœ² οÄ® οÄ© οÄ® οÄ©οÄ® οÄ©h x f g xοÄΫ οÄΪ .
Έ€ΈΩΈΫΈ§Έ¥ΈΒœ² 3
ΈΛΈïΈ¦ΈüΈΘ 3Έ½ΈΘ ΈëΈ†Έü 5 ΈΘΈïΈ¦ΈôΈîΈïΈΘ
10.01.2019 ΈëœÄΈΩΈΚΈΜΈΒΈΙœÉœ³ΈΙΈΚΈ§ œÉœ³ΈΩ lisari.blogspot.gr Page 3 of 5](https://image.slidesharecdn.com/prosomoiosi2019-kalamari-190110203745/85/2019-3-320.jpg)