Διαγώνισμα προσομοίωσης 2018 - Καλαμαρί
1 like14,843 views
Επιμέλεια: Ιωάννης Σαράφης αποκλειστικά για το lisari.blogspot.gr
![ΑΡΧΗ 3Η ΕΛΙΔΑ
Α3. Να χαρακτθρίςετε τισ προτάςεισ που ακολουκοφν, γράφοντασ ςτο τετράδιό
ςασ, δίπλα ςτο γράμμα που αντιςτοιχεί ςε κάκε πρόταςθ,τθ λζξθ ωστό ,αν θ
πρόταςθ είναι ςωςτι, ι Λάθος, αν θ πρόταςθ είναι λανκαςμζνθ.
α. Αν θ ςυνάρτθςθ f είναι ςυνεχισ ςτο , και υπάρχει 0x , τζτοιο ϊςτε
0f x 0 τότε f f 0 .
β. Αν για μια παραγωγίςιμθ ςυνάρτθςθ f ιςχφει ότι f x 0 για κάκε x ςε ζνα
διάςτθμα Δ, τότε θ f είναι γνθςίωσ μονότονθ ςτο Δ.
γ. Αν ιςχφει τουλάχιςτον μια ιςότθτα
0 0x x x x
lim f x , lim f x
, τότε θ
ευκεία 0x x λζγεται κατακόρυφθ αςφμπτωτθ τθσ γραφικισ παράςταςθσ τθσ f.
δ. Αν θ ςυνάρτθςθ f είναι παραγωγίςιμθ ςτο 0x ,τότε κα ιςχφει για κάκε ςυνάρτθςθ f
0
0
x x
lim f x f x
ε. Αν θ ςυνάρτθςθ f είναι ςυνεχισ [α,β] και f x dx 0
, τότε για κάκε ςυνάρτθςθ f
ιςχφει f x 0 για κάκε x , .
Moνάδες 10
ΘΕΜΑ Β
Δίνονται οι ςυναρτιςεισ
x
x
e 1
f x ln
1 e
, 3
g x x .
Β1. Να προςδιορίςετε τθ ςυνάρτθςθ g f .
Μονάδες 6
Β2. Να υπολογίςετε, αν υπάρχουν ,τα όρια :
2
2x xx 0
g x x
lim f x , lim f x , lim
x 1
Μονάδες 7
Β3. Να αποδείξετε ότι υπάρχει θ αντίςτροφθ τθσ f και να τθν βρείτε.
Μονάδες 12
ΣΕΛΟ 3Η ΑΠΟ 5 ΕΛΙΔΕ
17.04.2018 Αποκλειστικά στο lisari.blogspot.gr Page 3 of 5](https://image.slidesharecdn.com/prosomoiosi17-4-2018kalamari-180417044405/85/2018-3-320.jpg)
Διαγώνισμα προσομοίωσης 2018 - Καλαμαρί
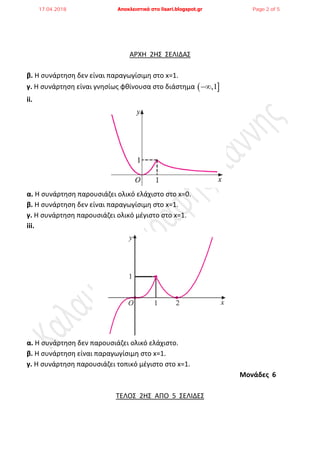
- 1. ΑΡΧΗ 1Η ΕΛΙΔΑ ΕΞΕΣΑΕΙ ΠΡΟΟΜΟΙΩΗ Γ' ΣΑΞΗ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ ΕΛΛΗΝΟΓΑΛΛΙΚΗ ΧΟΛΗ ΚΑΛΑΜΑΡΙ ΔΕΤΣΕΡΑ 16 ΑΠΡΙΛΙΟΤ 2018 ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:ΜΑΘΗΜΑΣΙΚΑ ΟΜΑΔΑ ΠΡΟΑΝΑΣΟΛΙΜΟΤ ΘΕΣΙΚΩΝ ΠΟΤΔΩΝ-ΟΙΚΟΝΟΜΙΑ & ΠΛΗΡΟΦΟΡΙΚΗ ΤΝΟΛΟ ΕΛΙΔΩΝ: ΠΕΝΣΕ (5) Εισηγητής : αράφης Γιάννης ΘΕΜΑ Α Α1. Ζςτω f μια ςυνάρτθςθ οριςμζνθ ςε ζνα διάςτθμα Δ. Αν F είναι μια παράγουςα τθσ f ςτο Δ, τότε να αποδείξετε ότι: ● όλεσ οι ςυναρτιςεισ τθσ μορφισ G x F x c , c , είναι παράγουςεσ τθσ f ςτο Δ και ● κάκε άλλθ παράγουςα G τθσ f ςτο Δ παίρνει τθ μορφι G x F x c , c Μονάδες 9 Α2. Δίνονται οι παρακάτω γραφικζσ παραςτάςεισ. Να γράψετε ςτο τετράδιό ςασ το γράμμα που αντιςτοιχεί ςτθν πρόταςθ που δεν ιςχφει για τθν αντίςτοιχθ γραφικι παράςταςθ: i. α. Η ςυνάρτθςθ παρουςιάηει ολικό ελάχιςτο ςτο x=1. ΣΕΛΟ 1Η ΑΠΟ 5 ΕΛΙΔΕ 17.04.2018 Αποκλειστικά στο lisari.blogspot.gr Page 1 of 5
- 2. ΑΡΧΗ 2Η ΕΛΙΔΑ β. Η ςυνάρτθςθ δεν είναι παραγωγίςιμθ ςτο x=1. γ. Η ςυνάρτθςθ είναι γνθςίωσ φκίνουςα ςτο διάςτθμα ,1 ii. α. Η ςυνάρτθςθ παρουςιάηει ολικό ελάχιςτο ςτο x=0. β. Η ςυνάρτθςθ δεν είναι παραγωγίςιμθ ςτο x=1. γ. Η ςυνάρτθςθ παρουςιάηει ολικό μζγιςτο ςτο x=1. iii. α. Η ςυνάρτθςθ δεν παρουςιάηει ολικό ελάχιςτο. β. Η ςυνάρτθςθ είναι παραγωγίςιμθ ςτο x=1. γ. Η ςυνάρτθςθ παρουςιάηει τοπικό μζγιςτο ςτο x=1. Μονάδες 6 ΣΕΛΟ 2Η ΑΠΟ 5 ΕΛΙΔΕ 17.04.2018 Αποκλειστικά στο lisari.blogspot.gr Page 2 of 5
- 3. ΑΡΧΗ 3Η ΕΛΙΔΑ Α3. Να χαρακτθρίςετε τισ προτάςεισ που ακολουκοφν, γράφοντασ ςτο τετράδιό ςασ, δίπλα ςτο γράμμα που αντιςτοιχεί ςε κάκε πρόταςθ,τθ λζξθ ωστό ,αν θ πρόταςθ είναι ςωςτι, ι Λάθος, αν θ πρόταςθ είναι λανκαςμζνθ. α. Αν θ ςυνάρτθςθ f είναι ςυνεχισ ςτο , και υπάρχει 0x , τζτοιο ϊςτε 0f x 0 τότε f f 0 . β. Αν για μια παραγωγίςιμθ ςυνάρτθςθ f ιςχφει ότι f x 0 για κάκε x ςε ζνα διάςτθμα Δ, τότε θ f είναι γνθςίωσ μονότονθ ςτο Δ. γ. Αν ιςχφει τουλάχιςτον μια ιςότθτα 0 0x x x x lim f x , lim f x , τότε θ ευκεία 0x x λζγεται κατακόρυφθ αςφμπτωτθ τθσ γραφικισ παράςταςθσ τθσ f. δ. Αν θ ςυνάρτθςθ f είναι παραγωγίςιμθ ςτο 0x ,τότε κα ιςχφει για κάκε ςυνάρτθςθ f 0 0 x x lim f x f x ε. Αν θ ςυνάρτθςθ f είναι ςυνεχισ [α,β] και f x dx 0 , τότε για κάκε ςυνάρτθςθ f ιςχφει f x 0 για κάκε x , . Moνάδες 10 ΘΕΜΑ Β Δίνονται οι ςυναρτιςεισ x x e 1 f x ln 1 e , 3 g x x . Β1. Να προςδιορίςετε τθ ςυνάρτθςθ g f . Μονάδες 6 Β2. Να υπολογίςετε, αν υπάρχουν ,τα όρια : 2 2x xx 0 g x x lim f x , lim f x , lim x 1 Μονάδες 7 Β3. Να αποδείξετε ότι υπάρχει θ αντίςτροφθ τθσ f και να τθν βρείτε. Μονάδες 12 ΣΕΛΟ 3Η ΑΠΟ 5 ΕΛΙΔΕ 17.04.2018 Αποκλειστικά στο lisari.blogspot.gr Page 3 of 5
- 4. ΑΡΧΗ 4Η ΕΛΙΔΑ ΘΕΜΑ Γ Δίνεται θ ςυνάρτθςθ 2 f x x 1 ln x , x 0 . Γ1. Να αποδείξετε ότι 1 2xln x x , για κάκε x 0 . Μονάδες 6 Γ2. Να λφςετε τθν εξίςωςθ f x 0 . Μονάδες 5 Γ3. Να αποδείξετε ότι υπάρχει μοναδικό 0 1 x ,1 e τζτοιο, ϊςτε το ςθμείο 0 0x ,f x να είναι ςθμείο καμπισ τθσ fC . Μονάδες 8 Γ4. Να υπολογίςετε το ολοκλιρωμα e 1 f x dx Μονάδες 6 ΘΕΜΑ Δ Δίνεται ιςοςκελζσ τρίγωνο ΑΒΓ με ΑΒ=ΑΓ=5 και ΒΓ=8.Σο ςθμείο Ε διαγράφει το ευκφγραμμο τμιμα ΒΓ με όπωσ φαίνεται ςτο παρακάτω ςχιμα. ΣΕΛΟ 4Η ΑΠΟ 5 ΕΛΙΔΕi 17.04.2018 Αποκλειστικά στο lisari.blogspot.gr Page 4 of 5
- 5. ΑΡΧΗ 5Η ΕΛΙΔΑ Δ1. Να αποδείξετε ότι το εμβαδόν του γραμμοςκιαςμζνου χωρίου που δθμιουργείται από το ευκφγραμμο τμιμα ΔΕ και τισ πλευρζσ του τριγϊνου ΑΒΓ ωσ ςυνάρτθςθ του x=ΒΕ είναι 2 2 3 x , 0<x 4 8 x 3 12 8 x , 4<x 8 8 Μονάδες 9 Δ2. Να εξετάςετε αν θ ςυνάρτθςθ x ζχει κρίςιμα ςθμεία ,αιτιολογϊντασ τθν απάντθςι ςασ . Μονάδες 5 Δ3. Να υπολογίςετε το x 0 1 E x xlim x Μονάδες 5 Δ4. Να υπολογίςετε το εμβαδόν του χωρίου που περικλείεται από τθ γραφικι παράςταςθ τθσ Ε , τθν εφαπτομζνθ ςτο ςθμείο Μ(4,6) και τισ ευκείεσ x=4 και x=6. Μονάδες 6 ΣΕΛΟ 5Η ΑΠΟ 5 ΕΛΙΔΕ 17.04.2018 Αποκλειστικά στο lisari.blogspot.gr Page 5 of 5