ąøąĄą║čåąĖčÅ 4
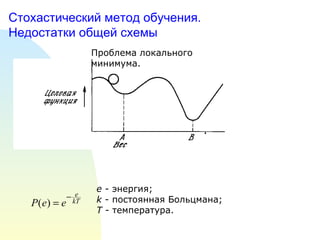
- 1. ąøąĄą║čåąĖčÅ 4 . ąÉą╗ą│ąŠčĆąĖčéą╝ ąŠą▒čĆą░čéąĮąŠą│ąŠ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖčÅ ąŠčłąĖą▒ą║ąĖ. ą×ą▒ąĘąŠčĆ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą▓ ąŠą▒čāč湥ąĮąĖčÅ
- 2. ąÜą╗ą░čüčüąĖčäąĖą║ą░čåąĖčÅ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą▓ ąŠą▒čāč湥ąĮąĖčÅ 1. ążąĖą║čüąĖčĆąŠą▓ą░ąĮąĮčŗąĄ ą▓ąĄčüą░. ąÆąĄčüą░ čüąĄčéąĖ ą▓čŗčćąĖčüą╗čÅčÄčéčüčÅ ąĘą░čĆą░ąĮąĄąĄ ąĖ ąĮąĄ ąĖąĘą╝ąĄąĮčÅčÄčéčüčÅ ą▓ ą┐čĆąŠčåąĄčüčüąĄ ąŠą▒čāč湥ąĮąĖčÅ. 2. ą×ą▒čāč湥ąĮąĖąĄ čü čāčćąĖč鹥ą╗ąĄą╝. ą×ą▒čāčćą░čÄčēą░čÅ ą▓čŗą▒ąŠčĆą║ą░ čüąŠą┤ąĄčƹȹĖčé ą▓čģąŠą┤ąĮčŗąĄ čüąĖą│ąĮą░ą╗čŗ, ą░ čéą░ą║ąČąĄ ąŠąČąĖą┤ą░ąĄą╝čŗąĄ ą▓čŗčģąŠą┤ąĮčŗąĄ čüąĖą│ąĮą░ą╗čŗ. ą¤ąŠą┤ą▒ąŠčĆ ą▓ąĄčüąŠą▓ ąŠčĆą│ą░ąĮąĖąĘąŠą▓ą░ąĮ čéą░ą║, čćč鹊ą▒čŗ čĆąĄą░ą╗čīąĮčŗąĄ ą▓čŗčģąŠą┤čŗ čüąĄčéąĖ ą▒čŗą╗ąĖ ą║ą░ą║ ą╝ąŠąČąĮąŠ ą▒ą╗ąĖąČąĄ ą║ ąŠąČąĖą┤ą░ąĄą╝čŗą╝ ą▓čŗčģąŠą┤ą░ą╝. 3. ą×ą▒čāč湥ąĮąĖąĄ ą▒ąĄąĘ čāčćąĖč鹥ą╗čÅ. ąØąĄčé ąĘąĮą░ąĮąĖą╣ ąŠ ąČąĄą╗ą░ąĄą╝čŗčģ ą▓čŗčģąŠą┤ą░čģ čüąĄčéąĖ. - ą║ąŠąĮą║čāčĆąĄąĮčåąĖčÅ ąĮąĄą╣čĆąŠąĮąŠą▓ ą╝ąĄąČą┤čā čüąŠą▒ąŠą╣: Winner takes all (WTA); Winner takes most (WTM) . - čāč湥čé ą║ąŠčĆčĆąĄą╗čÅčåąĖąĖ ąŠą▒čāčćą░čÄčēąĖčģ ąĖ ą▓čŗčģąŠą┤ąĮčŗčģ čüąĖą│ąĮą░ą╗ąŠą▓ (ąŠą▒čāč湥ąĮąĖąĄ ą┐ąŠ ąźąĄą▒ą▒čā).
- 3. ąÉą╗ą│ąŠčĆąĖčéą╝ ąŠą▒čĆą░čéąĮąŠą│ąŠ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖčÅ ąŠčłąĖą▒ą║ąĖ ąśąĮąĖčåąĖą░ą╗ąĖąĘąĖčĆąŠą▓ą░čéčī ą▓ąĄčüą░ čüąĄčéąĖ ąÆčŗą▒čĆą░čéčī ąŠą▒čāčćą░čÄčēčāčÄ ą┐ą░čĆčā ąĖąĘ ąŠą▒čāčćą░čÄčēąĄą│ąŠ ą╝ąĮąŠąČąĄčüčéą▓ą░. ą¤ąŠą┤ą░čéčī ąĮą░ ą▓čģąŠą┤ čüąĄčéąĖ, ą▓čŗčćąĖčüą╗ąĖčéčī ą▓čŗčģąŠą┤ ąÆčŗčćąĖčüą╗ąĖčéčī čĆą░ąĘąĮąŠčüčéčī ą╝ąĄąČą┤čā čĆąĄą░ą╗čīąĮčŗą╝ ą▓čŗčģąŠą┤ąŠą╝ ąĖ čéčĆąĄą▒čāąĄą╝čŗą╝ ą▓čŗčģąŠą┤ąŠą╝ ą¤ąŠą┤ą║ąŠčĆčĆąĄą║čéąĖčĆąŠą▓ą░čéčī ą▓ąĄčüą░ čüąĄčéąĖ, čéą░ą║ čćč鹊ą▒čŗ čāą╝ąĄąĮčīčłąĖčéčī ąŠčłąĖą▒ą║čā ą¤ąŠą▓č鹊čĆčÅčéčī čłą░ą│ąĖ 2-5 ą┤ą╗čÅ ą║ą░ąČą┤ąŠą│ąŠ ą▓ąĄą║č鹊čĆą░ ąĖąĘ ąŠą▒čāčćą░čÄčēąĄą│ąŠ ą╝ąĮąŠąČąĄčüčéą▓ą░, ą┐ąŠą║ą░ ąŠčłąĖą▒ą║ą░ ąĮąĄ ą┤ąŠčüčéąĖą│ąĮąĄčé ą┐čĆąĖąĄą╝ą╗ąĄą╝ąŠą│ąŠ čāčĆąŠą▓ąĮčÅ ą©ą░ą│ąĖ 2, 3 ŌĆō ą┐čĆąŠčģąŠą┤ ą▓ą┐ąĄčĆąĄą┤ ą©ą░ą│ąĖ 4, 5 ŌĆō ąŠą▒čĆą░čéąĮčŗą╣ ą┐čĆąŠčģąŠą┤
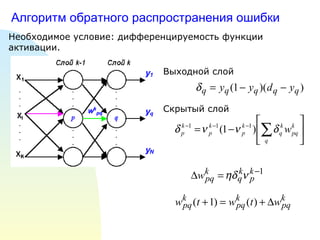
- 4. ąÉą╗ą│ąŠčĆąĖčéą╝ ąŠą▒čĆą░čéąĮąŠą│ąŠ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖčÅ ąŠčłąĖą▒ą║ąĖ ąØąĄąŠą▒čģąŠą┤ąĖą╝ąŠąĄ čāčüą╗ąŠą▓ąĖąĄ: ą┤ąĖčäč乥čĆąĄąĮčåąĖčĆčāąĄą╝ąŠčüčéčī čäčāąĮą║čåąĖąĖ ą░ą║čéąĖą▓ą░čåąĖąĖ. ąÆčŗčģąŠą┤ąĮąŠą╣ čüą╗ąŠą╣ ąĪą║čĆčŗčéčŗą╣ čüą╗ąŠą╣
- 5. ąÉą╗ą│ąŠčĆąĖčéą╝ ąŠą▒čĆą░čéąĮąŠą│ąŠ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖčÅ ąŠčłąĖą▒ą║ąĖ ą£ąĖąĮąĖą╝ąĖąĘą░čåąĖčÅ čåąĄą╗ąĄą▓ąŠą╣ čäčāąĮą║čåąĖąĖ : d - ąČąĄą╗ą░ąĄą╝čŗą╣ ą▓čŗčģąŠą┤ y - čĆąĄą░ą╗čīąĮčŗą╣ ą▓čŗčģąŠą┤ ą£ąĄč鹊ą┤ ąŠą▒čāč湥ąĮąĖčÅ - ą│čĆą░ą┤ąĖąĄąĮčéąĮčŗą╣ čüą┐čāčüą║ . ąÆčŗčģąŠą┤ąĮąŠą╣ čüą╗ąŠą╣
- 6. ąÉą╗ą│ąŠčĆąĖčéą╝ ąŠą▒čĆą░čéąĮąŠą│ąŠ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖčÅ ąŠčłąĖą▒ą║ąĖ 1. ąĀą░čüčüčćąĖčéą░čéčī ą▓čŗčģąŠą┤čŗ čüąĄčéąĖ. 2. ąĀą░čüčüčćąĖčéą░čéčī ą┤ą╗čÅ ą▓čŗčģąŠą┤ąĮąŠą│ąŠ čüą╗ąŠčÅ: 3. ąĀą░čüčüčćąĖčéą░čéčī ą┤ą╗čÅ ą▓čüąĄčģ ąŠčüčéą░ą╗čīąĮčŗčģ čüą╗ąŠąĄą▓: 4. ąĪą║ąŠčĆčĆąĄą║čéąĖčĆąŠą▓ą░čéčī ą▓ąĄčüą░: 5. ąĢčüą╗ąĖ ąŠčłąĖą▒ą║ą░ čüčāčēąĄčüčéą▓ąĄąĮąĮą░, ą┐ąĄčĆąĄą╣čéąĖ ąĮą░ čłą░ą│ 1.
- 7. ąÉą╗ą│ąŠčĆąĖčéą╝ ąŠą▒čĆą░čéąĮąŠą│ąŠ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖčÅ ąŠčłąĖą▒ą║ąĖ ą¤čĆąŠą▒ą╗ąĄą╝čŗ: 1. ą¤ą░čĆą░ą╗ąĖčć čüąĄčéąĖ. 2. ą×ą▒ąĮą░čĆčāąČąĄąĮąĖąĄ ą╗ąŠą║ą░ą╗čīąĮąŠą│ąŠ ą╝ąĖąĮąĖą╝čāą╝ą░. 3. ąÆčŗą▒ąŠčĆ čüą║ąŠčĆąŠčüčéąĖ ąŠą▒čāč湥ąĮąĖčÅ.
- 8. ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą╝ąŠą╝ąĄąĮčéą░ ą×ą┤ąĖąĮ ąĖąĘ čüą┐ąŠčüąŠą▒ąŠą▓ čāčüą║ąŠčĆąĖčéčī čüčģąŠą┤ąĖą╝ąŠčüčéčī ą░ą╗ą│ąŠčĆąĖčéą╝ą░ ąŠą▒čĆą░čéąĮąŠą│ąŠ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖčÅ ąŠčłąĖą▒ą║ąĖ. ąĪą┤ąĄą╗ą░ąĄą╝ čĆąĄą║čāčĆčĆąĄąĮčéąĮčŗąĄ ą┐ąŠą┤čüčéą░ąĮąŠą▓ą║ąĖ. ąÆą▓ąĄą┤ąĄą╝ čĆčÅą┤ ą┐ąŠ t . ąĀąĄčłąĖą╝ čĆą░ąĘąĮąŠčüčéąĮąŠąĄ čāčĆą░ą▓ąĮąĄąĮąĖąĄ.
- 9. ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą╝ąŠą╝ąĄąĮčéą░ (2) ąöą╗čÅ čüčģąŠą┤ąĖą╝ąŠčüčéąĖ čĆčÅą┤ą░ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠ ąŻčüą║ąŠčĆčÅąĄčé čüą┐čāčüą║, ąĄčüą╗ąĖ ąĘąĮą░ą║ ą│čĆą░ą┤ąĖąĄąĮčéą░ ąĮąĄ ą╝ąĄąĮčÅąĄčéčüčÅ ąŚą░ą╝ąĄą┤ą╗čÅąĄčé čüą┐čāčüą║, ąĄčüą╗ąĖ ąĘąĮą░ą║ ą│čĆą░ą┤ąĖąĄąĮčéą░ ąĖąĘą╝ąĄąĮčÅąĄčéčüčÅ ŌĆō čüčéą░ą▒ąĖą╗ąĖąĘąĖčĆčāčÄčēąĖą╣ čŹčäč乥ą║čé. ą¤ąŠą╝ąŠą│ą░ąĄčé ąĖąĘą▒ąĄąČą░čéčī ą╗ąŠą║ą░ą╗čīąĮčŗčģ ą╝ąĖąĮąĖą╝čāą╝ąŠą▓
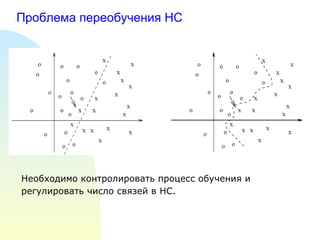
- 10. ą¤čĆąŠą▒ą╗ąĄą╝ą░ ą┐ąĄčĆąĄąŠą▒čāč湥ąĮąĖčÅ ąØąĪ ąØąĄąŠą▒čģąŠą┤ąĖą╝ąŠ ą║ąŠąĮčéčĆąŠą╗ąĖčĆąŠą▓ą░čéčī ą┐čĆąŠčåąĄčüčü ąŠą▒čāč湥ąĮąĖčÅ ąĖ čĆąĄą│čāą╗ąĖčĆąŠą▓ą░čéčī čćąĖčüą╗ąŠ čüą▓čÅąĘąĄą╣ ą▓ ąØąĪ.
- 11. ą×ą▒čāčćą░čÄčēą░čÅ ąĖ ą┐ąŠą┤čéą▓ąĄčƹȹ┤ą░čÄčēą░čÅ ą▓čŗą▒ąŠčĆą║ąĖ S L ŌĆō ąŠą▒čāčćą░čÄčēą░čÅ ą▓čŗą▒ąŠčĆą║ą░ ; E learn ŌĆō ąŠčłąĖą▒ą║ą░ ąĮą░ ąŠą▒čāčćą░čÄčēąĄą╣ ą▓čŗą▒ąŠčĆą║ąĄ ; S V ŌĆō ą┐ąŠą┤čéą▓ąĄčƹȹ┤ą░čÄčēą░čÅ ą▓čŗą▒ąŠčĆą║ą░ ; E val ŌĆō ąŠčłąĖą▒ą║ą░ ąĮą░ ą┐ąŠą┤čéą▓ąĄčƹȹ┤ą░čÄčēąĄą╣ ą▓čŗą▒ąŠčĆą║ąĄ ; ąØąĄąŠą▒čģąŠą┤ąĖą╝ąŠ, čćč鹊ą▒čŗ E learn ąĖ E val ą▓ ą║ąŠąĮčåąĄ ąŠą▒čāč湥ąĮąĖčÅ ą┤ąŠčüčéąĖą│ą╗ąĖ ą╝ąĖąĮąĖą╝čāą╝ą░
- 12. ą£ąĄč鹊ą┤čŗ čĆąĄą┤čāą║čåąĖąĖ čüąĄčéąĖ čü čāč湥č鹊ą╝ čćčāą▓čüčéą▓ąĖč鹥ą╗čīąĮąŠčüčéąĖ ( OBD) ąÜąŠčŹčäčäąĖčåąĖąĄąĮčé ą░čüčüąĖą╝ąĄčéčĆąĖąĖ: ą×ą▒čāčćąĖčéčī čüąĄčéčī ąÆčŗčćąĖčüą╗ąĖčéčī ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéčŗ ą░čüčüąĖą╝ąĄčéčĆąĖąĖ ą┤ą╗čÅ ą║ą░ąČą┤ąŠą╣ čüą▓čÅąĘąĖ ą×čéčüąĄčćčī ą▓ąĄčüą░ čü ąĮą░ąĖą╝ąĄąĮčīčłąĖą╝ąĖ ąĘąĮą░č湥ąĮąĖčÅą╝ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ ą¤ąĄčĆąĄą╣čéąĖ ąĮą░ ą┐.1 ą¤čĆąŠą┤ąŠą╗ąČą░čéčī čåąĖą║ą╗ ą┐ąŠą║ą░ ą▓čüąĄ ą▓ąĄčüą░, ąŠą║ą░ąĘčŗą▓ą░čÄčēąĖąĄ ąĮą░ąĖą╝ąĄąĮčīčłąĄąĄ ą▓ą╗ąĖčÅąĮąĖąĄ ąĮąĄ ą▒čāą┤čāčé čāą┤ą░ą╗ąĄąĮčŗ
- 13. ą£ąĄč鹊ą┤čŗ čĆąĄą┤čāą║čåąĖąĖ čüąĄčéąĖ čü ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ čłčéčĆą░čäąĮąŠą╣ čäčāąĮą║čåąĖąĖ - ą╝ąĄč鹊ą┤ Weight Decay ; - ą╝ąĄč鹊ą┤ Weight Elimination
- 14. ąōčĆą░ą┤ąĖąĄąĮčéąĮčŗąĄ ą╝ąĄč鹊ą┤čŗ ąŠą▒čāč湥ąĮąĖčÅ H(w) - ą╝ą░čéčĆąĖčåą░ ą▓č鹊čĆčŗčģ ą┐čĆąŠąĖąĘą▓ąŠą┤ąĮčŗčģ; ą”ąĄą╗čī: ą┐ąŠą┤ąŠą▒čĆą░čéčī p ąĖ ’ü© čéą░ą║, čćč鹊ą▒čŗ, ą┤ą╗čÅ ąŠč湥čĆąĄą┤ąĮąŠą╣ č鹊čćą║ąĖ w k+1 ą▓čŗą┐ąŠą╗ąĮčÅą╗ąŠčüčī čāčüą╗ąŠą▓ąĖąĄ: ą×ą▒ąŠąĘąĮą░čćąĖą╝ w k -čĆąĄčłąĄąĮąĖąĄ, ą┐ąŠą╗čāč湥ąĮąĮąŠąĄ ąĮą░ k -ąŠą╝ čłą░ą│ąĄ. w ą╝ąĖąĮąĖą╝čāą╝ E(w) , ąĄčüą╗ąĖ g(w)=0, H(w) ŌĆō ą┐ąŠą╗ąŠąČąĖč鹥ą╗čīąĮąŠ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮą░ ą£ąĖąĮąĖą╝ąĖąĘą░čåąĖčÅ čåąĄą╗ąĄą▓ąŠą╣ čäčāąĮą║čåąĖąĖ : d - ąČąĄą╗ą░ąĄą╝čŗą╣ ą▓čŗčģąŠą┤ y - čĆąĄą░ą╗čīąĮčŗą╣ ą▓čŗčģąŠą┤ ą£ąĄč鹊ą┤ ąŠą▒čāč湥ąĮąĖčÅ - ą│čĆą░ą┤ąĖąĄąĮčéąĮčŗą╣ čüą┐čāčüą║.
- 15. ąĪčģąĄą╝ą░ čāąĮąĖą▓ąĄčĆčüą░ą╗čīąĮąŠą│ąŠ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ ąŠą▒čāč湥ąĮąĖčÅ 1. ą¤čĆąŠą▓ąĄčĆą║ą░ ąŠą┐čéąĖą╝ą░ą╗čīąĮąŠčüčéąĖ č鹥ą║čāčēąĄą│ąŠ čĆąĄčłąĄąĮąĖčÅ w k . 2. ą×ą┐čĆąĄą┤ąĄą╗ąĄąĮąĖąĄ ą▓ąĄą║č鹊čĆą░ ąĮą░ą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ąŠą┐čéąĖą╝ąĖąĘą░čåąĖąĖ p k ą┤ą╗čÅ č鹊čćą║ąĖ w k . 3. ąÆčŗą▒ąŠčĆ čłą░ą│ą░ ’ü© k ą▓ ąĮą░ą┐čĆą░ą▓ą╗ąĄąĮąĖąĖ p k , ą┐čĆąĖ ą║ąŠč鹊čĆąŠą╝ ą▓čŗą┐ąŠą╗ąĮčÅąĄčéčüčÅ čāčüą╗ąŠą▓ąĖąĄ E(w k+1 )< E(w k ) 4. ą×ą┐čĆąĄą┤ąĄą╗ąĄąĮąĖąĄ ąĮąŠą▓ąŠą│ąŠ čĆąĄčłąĄąĮąĖčÅ ą░ čéą░ą║ąČąĄ čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēąĖčģ ąĄą╝čā ąĘąĮą░č湥ąĮąĖą╣ čäčāąĮą║čåąĖąĖ ąŠčłąĖą▒ą║ąĖ, ą│čĆą░ą┤ąĖąĄąĮčéą░, ą╝ą░čéčĆąĖčåčŗ ą▓č鹊čĆčŗčģ ą┐čĆąŠąĖąĘą▓ąŠą┤ąĮčŗčģ. ą¤ąĄčĆąĄčģąŠą┤ ąĮą░ 1.
- 16. ąÉą╗ą│ąŠčĆąĖčéą╝ ąĮą░ąĖčüą║ąŠčĆąĄą╣čłąĄą│ąŠ čüą┐čāčüą║ą░ ąøąĖąĮąĄą╣ąĮąŠąĄ ą┐čĆąĖą▒ą╗ąĖąČąĄąĮąĖąĄ čäčāąĮą║čåąĖąĖ E(w) . ąöą╗čÅ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖčÅ čāčüą╗ąŠą▓ąĖčÅ E(w k+1 )< E(w k ) , ąĮą░ą┤ąŠ ąöąŠčüč鹊ąĖąĮčüčéą▓ą░: - ąĮąĄą▒ąŠą╗čīčłą░čÅ ą▓čŗčćąĖčüą╗ąĖč鹥ą╗čīąĮą░čÅ čüą╗ąŠąČąĮąŠčüčéčī; - ąĮąĄą▓čŗčüąŠą║ąĖąĄ čéčĆąĄą▒ąŠą▓ą░ąĮąĖčÅ ą║ ą┐ą░ą╝čÅčéąĖ. ąØąĄą┤ąŠčüčéą░čéą║ąĖ: - ąĮąĄ čāčćąĖčéčŗą▓ą░ąĄčé ąĖąĮč乊čĆą╝ą░čåąĖčÄ ąŠ ą║čĆąĖą▓ąĖąĘąĮąĄ čäčāąĮą║čåąĖąĖ; - ąĘą░ą╝ąĄą┤ą╗ąĄąĮąĖąĄ ą▓ čüą╗čāčćą░ąĄ ą╝ą░ą╗ąĄąĮčīą║ąŠą│ąŠ ą│čĆą░ą┤ąĖąĄąĮčéą░; - ą╝ąĄą┤ą╗ąĄąĮąĮą░čÅ čüčģąŠą┤ąĖą╝ąŠčüčéčī.
- 17. ąØą░ąĖčüą║ąŠčĆąĄą╣čłąĖą╣ čüą┐čāčüą║ čü ą╝ąŠą╝ąĄąĮč鹊ą╝ ’üĪ - ą║ąŠčŹčäčäąĖčåąĖąĄąĮčé ą╝ąŠą╝ąĄąĮčéą░ ą▓ ąĖąĮč鹥čĆą▓ą░ą╗ąĄ [0,1] ąØą░ ą┐ą╗ąŠčüą║ąĖčģ čāčćą░čüčéą║ą░čģ: ąŻčüą╗ąŠą▓ąĖąĄ čāč湥čéą░ ą╝ąŠą╝ąĄąĮčéą░ ą▓ ą┐čĆąĖčĆą░čēąĄąĮąĖąĖ ą▓ąĄčüąŠą▓ (ą┐čĆąĖą╝ąĄčĆ): ąöąŠčüč鹊ąĖąĮčüčéą▓ąŠ: čāčüą║ąŠčĆąĄąĮąĖąĄ čüčģąŠą┤ąĖą╝ąŠčüčéąĖ ąĮą░ ą┐ą╗ąŠčüą║ąĖčģ čāčćą░čüčéą║ą░čģ ąĖ ą▓ą▒ą╗ąĖąĘąĖ ą╗ąŠą║ą░ą╗čīąĮčŗčģ 菹║čüčéčĆąĄą╝čāą╝ąŠą▓.
- 18. ą£ąĄč鹊ą┤ ą┐ąĄčĆąĄą╝ąĄąĮąĮąŠą╣ ą╝ąĄčéčĆąĖą║ąĖ ąÜą▓ą░ą┤čĆą░čéąĖčćąĮąŠąĄ ą┐čĆąĖą▒ą╗ąĖąČąĄąĮąĖąĄ E(w) ąśčüą┐ąŠą╗čīąĘčāčÄčé ą┐čĆąĖą▒ą╗ąĖąČąĄąĮąĖąĄ H(w) : ą│ą┤ąĄ: V k - ą┐čĆąĖą▒ą╗ąĖąČąĄąĮąĖąĄ ąöąŠčüč鹊ąĖąĮčüčéą▓ąŠ: ą▒čŗčüčéčĆą░čÅ čüčģąŠą┤ąĖą╝ąŠčüčéčī. ąØąĄą┤ąŠčüčéą░čéą║ąĖ: - ą▓čŗčćąĖčüą╗ąĖč鹥ą╗čīąĮą░čÅ čüą╗ąŠąČąĮąŠčüčéčī; - čéčĆąĄą▒ąŠą▓ą░ąĮąĖčÅ ą║ ą┐ą░ą╝čÅčéąĖ.
- 19. ąÉą╗ą│ąŠčĆąĖčéą╝ čüąŠą┐čĆčÅąČąĄąĮąĮčŗčģ ą│čĆą░ą┤ąĖąĄąĮč鹊ą▓ ąØą░ą┐čĆą░ą▓ą╗ąĄąĮąĖąĄ ą┐ąŠąĖčüą║ą░ p k ą▓čŗą▒ąĖčĆą░ąĄčéčüčÅ čéą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝, čćč鹊ą▒čŗ ąŠąĮąŠ ą▒čŗą╗ąŠ ąŠčĆč鹊ą│ąŠąĮą░ą╗čīąĮčŗą╝ ąĖ čüąŠą┐čĆčÅąČąĄąĮąĮčŗą╝ ą║ąŠ ą▓čüąĄą╝ ą┐čĆąĄą┤čŗą┤čāčēąĖą╝ ąĮą░ą┐čĆą░ą▓ą╗ąĄąĮąĖčÅą╝ p 0 , p 1 ,ŌĆ”, p k-1 . ąöąŠčüč鹊ąĖąĮčüčéą▓ąŠ: - ą▒čŗčüčéčĆąĄąĄ ąĮą░ąĖčüą║ąŠčĆąĄą╣čłąĄą│ąŠ čüą┐čāčüą║ą░; - ąĮąĄą▓čŗčüąŠą║ąĖąĄ čéčĆąĄą▒ąŠą▓ą░ąĮąĖčÅ ą║ ą┐ą░ą╝čÅčéąĖ. ąØąĄą┤ąŠčüčéą░č鹊ą║: ą╝ąĄąĮąĄąĄ čŹčäč乥ą║čéąĖą▓ąĄąĮ ą╝ąĄč鹊ą┤ą░ ą┐ąĄčĆąĄą╝ąĄąĮąĮąŠą╣ ą╝ąĄčéčĆąĖą║ąĖ.
- 20. ąÉą╗ą│ąŠčĆąĖčéą╝ Quickprop ’ü¦ - ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčéčüčÅ ą┐ąŠą╗čīąĘąŠą▓ą░č鹥ą╗ąĄą╝ (10 -4 ) ’ü© k =0 , ąĄčüą╗ąĖ k>0 ąĖ
- 21. ąŻą┐čĆąŠčēąĄąĮąĮą░čÅ ą▓ąĄčĆčüąĖčÅ Quickprop
- 23. ą¤čĆąŠčüč鹥ą╣čłąĖąĄ ą╝ąĄč鹊ą┤čŗ ą┐ąŠą┤ą▒ąŠčĆą░ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéą░ ąŠą▒čāč湥ąĮąĖčÅ ąĢčüą╗ąĖ , č鹊 ąĢčüą╗ąĖ , č鹊
- 24. ą¤ąŠą┤ą▒ąŠčĆ ąĮą░ ąŠčüąĮąŠą▓ąĄ ąĮą░ą┐čĆą░ą▓ą╗ąĄąĮąĮąŠą╣ ą╝ąĖąĮąĖą╝ąĖąĘą░čåąĖąĖ
- 25. ąĪč鹊čģą░čüčéąĖč湥čüą║ąĖą╣ ą╝ąĄč鹊ą┤ ąŠą▒čāč湥ąĮąĖčÅ. ą×ą▒čēą░čÅ čüčģąĄą╝ą░ 1. ąÆčŗą┐ąŠą╗ąĮąĖčéčī ąĮą░čćą░ą╗čīąĮčāčÄ ąĖąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÄ ą▓ąĄčüąŠą▓. 2. ąÆčŗčćąĖčüą╗ąĖčéčī ą▓čŗčģąŠą┤ ą┤ą╗čÅ ą┐čĆąĖą╝ąĄčĆą░ ąĖąĘ ąŠą▒čāčćą░čÄčēąĄą╣ ą▓čŗą▒ąŠčĆą║ąĖ. 3. ąÆčŗčćąĖčüą╗ąĖčéčī ąŠčłąĖą▒ą║čā: 4. ąÆčŗą▒čĆą░čéčī čüą╗čāčćą░ą╣ąĮčŗą╝ ąŠą▒čĆą░ąĘąŠą╝ ą▓ąĄčü ąĖ ąĖąĘą╝ąĄąĮąĖčéčī ąĄą│ąŠ ąĘąĮą░č湥ąĮąĖąĄ ąĮą░ čüą╗čāčćą░ą╣ąĮčāčÄ ą▓ąĄą╗ąĖčćąĖąĮčā. ąĢčüą╗ąĖ ą┐čĆąŠą▓ąĄą┤ąĄąĮąĮąŠąĄ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ čāą╝ąĄąĮčīčłą░ąĄčé čåąĄą╗ąĄą▓čāčÄ čäčāąĮą║čåąĖčÄ (ąŠčłąĖą▒ą║čā), č鹊 čüąŠčģčĆą░ąĮąĖčéčī ąĄą│ąŠ, ąĖąĮą░č湥 ą▓ąĄčĆąĮčāčéčīčüčÅ ą║ ą┐čĆąĄąČąĮąĄą╝čā ąĘąĮą░č湥ąĮąĖčÄ ą▓ąĄčüą░. 5. ą¤ąŠą▓č鹊čĆčÅčéčī čłą░ą│ąĖ 2, 3, 4, ą┐ąŠą║ą░ čüąĄčéčī ąĮąĄ ąŠą▒čāčćąĖčéčüčÅ.
- 26. ąĪč鹊čģą░čüčéąĖč湥čüą║ąĖą╣ ą╝ąĄč鹊ą┤ ąŠą▒čāč湥ąĮąĖčÅ. ąØąĄą┤ąŠčüčéą░čéą║ąĖ ąŠą▒čēąĄą╣ čüčģąĄą╝čŗ ą¤čĆąŠą▒ą╗ąĄą╝ą░ ą╗ąŠą║ą░ą╗čīąĮąŠą│ąŠ ą╝ąĖąĮąĖą╝čāą╝ą░. e - 菹ĮąĄčĆą│ąĖčÅ; k - ą┐ąŠčüč鹊čÅąĮąĮą░čÅ ąæąŠą╗čīčåą╝ą░ąĮą░; T - č鹥ą╝ą┐ąĄčĆą░čéčāčĆą░.
- 27. ąÉą╗ą│ąŠčĆąĖčéą╝ ąĖą╝ąĖčéą░čåąĖąĖ ąŠčéąČąĖą│ą░ 1. ąÆčŗą┐ąŠą╗ąĮąĖčéčī ąĮą░čćą░ą╗čīąĮčāčÄ ąĖąĮąĖčåąĖą░ą╗ąĖąĘą░čåąĖčÄ ą▓ąĄčüąŠą▓. ąŚą░ą┤ą░čéčī ąĮą░čćą░ą╗čīąĮčāčÄ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčā T=T max . ąÆčŗčćąĖčüą╗ąĖčéčī ąĘąĮą░č湥ąĮąĖąĄ ąŠčłąĖą▒ą║ąĖ. 2 . ą¤ąŠą║ą░ T>0 ą┐ąŠą▓č鹊čĆąĖčéčī L čĆą░ąĘ ą┤ąĄą╣čüčéą▓ąĖčÅ: 2.1. ąÆčŗą┐ąŠą╗ąĮąĖčéčī čüą╗čāčćą░ą╣ąĮčāčÄ ą║ąŠčĆčĆąĄą║čåąĖčÄ ą▓ąĄčüąŠą▓ wŌĆÖ=w+ ’üä w . 2.2. ąÆčŗčćąĖčüą╗ąĖčéčī čĆą░ąĘąĮąĖčåčā čåąĄą╗ąĄą▓čŗčģ čäčāąĮą║čåąĖą╣ c=E(wŌĆÖ)-E(w) . 2.3. ąĢčüą╗ąĖ čü <0 , č鹊 w=wŌĆÖ ąĖąĮą░č湥 ą┐čĆąĖąĮčÅčéčī w=wŌĆÖ čü ą▓ąĄčĆąŠčÅčéąĮąŠčüčéčīčÄ 3. ąŻą╝ąĄąĮčīčłąĖčéčī č鹥ą╝ą┐ąĄčĆą░čéčāčĆčā T . 4. ą¤ąŠą▓č鹊čĆčÅčéčī 2, 3, 4 ą┐ąŠą║ą░ ąó>0 ąĖą╗ąĖ ąĘąĮą░č湥ąĮąĖąĄ ąŠčłąĖą▒ą║ąĖ ą▒ąŠą╗čīčłąĄ ą┐ąŠčĆąŠą│ą░. ą¤čĆąĖčĆą░čēąĄąĮąĖąĄ ą▓ąĄčüąŠą▓ ’üä w :
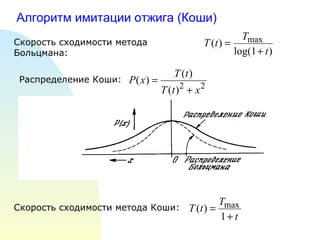
- 28. ąÉą╗ą│ąŠčĆąĖčéą╝ ąĖą╝ąĖčéą░čåąĖąĖ ąŠčéąČąĖą│ą░ (ąÜąŠčłąĖ) ąĪą║ąŠčĆąŠčüčéčī čüčģąŠą┤ąĖą╝ąŠčüčéąĖ ą╝ąĄč鹊ą┤ą░ ąæąŠą╗čīčåą╝ą░ąĮą░: ąĀą░čüą┐čĆąĄą┤ąĄą╗ąĄąĮąĖąĄ ąÜąŠčłąĖ: ąĪą║ąŠčĆąŠčüčéčī čüčģąŠą┤ąĖą╝ąŠčüčéąĖ ą╝ąĄč鹊ą┤ą░ ąÜąŠčłąĖ:
- 29. ąÆčŗą▒ąŠčĆ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą▓ ą░ą╗ą│ąŠčĆąĖčéą╝ą░ ąĖą╝ąĖčéą░čåąĖąĖ ąŠčéąČąĖą│ą░ 1. ą¤čĆąĖčĆą░čēąĄąĮąĖąĄ ą▓ąĄčüąŠą▓ ’üä w . 2. ąØą░čćą░ą╗čīąĮą░čÅ č鹥ą╝ą┐ąĄčĆą░čéčāčĆą░ T max . 3. ąÜąŠą╗ąĖč湥čüčéą▓ąŠ čåąĖą║ą╗ąŠą▓ L . 4. ąĪą║ąŠčĆąŠčüčéčī čāą╝ąĄąĮčīčłąĄąĮąĖčÅ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčŗ.
- 30. ąÜąŠą╝ą▒ąĖąĮąĖčĆąŠą▓ą░ąĮąĮčŗą╣ ą╝ąĄč鹊ą┤ ąŠą▒čāč湥ąĮąĖčÅ ą×ą▒čŖąĄą┤ąĖąĮąĄąĮąĖąĄ čéčĆą░ą┤ąĖčåąĖąŠąĮąĮąŠą│ąŠ ąŠą▒čĆą░čéąĮąŠą│ąŠ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖčÅ čü ąŠą▒čāč湥ąĮąĖąĄą╝ ąÜąŠčłąĖ. ą¤čĆąĄąŠą┤ąŠą╗ąĄąĮąĖąĄ čüąĄč鹥ą▓ąŠą│ąŠ ą┐ą░čĆą░ą╗ąĖčćą░:
Editor's Notes
- #8: ąĢčüą╗ąĖ ą▓čŗčģąŠą┤čŗ ąĮąĄą╣čĆąŠąĮąŠą▓ ą▒ą╗ąĖąĘą║ąĖ ą║ ąĮčāą╗čÄ, č鹊 ąŠą▒čāč湥ąĮąĖąĄ ąĘą░ą╝ąĄą┤ą╗čÅąĄčéčüčÅ. ąÜčĆą░čéą║ąŠą▓čĆąĄą╝ąĄąĮąĮąŠąĄ čāą▓ąĄą╗ąĖč湥ąĮąĖąĄ čüą║ąŠčĆąŠčüčéąĖ ąŠą▒čāč湥ąĮąĖčÅ ą┤ą╗čÅ ąĮąŠą▓ąŠą╣ ą┐ąŠą┐čŗčéą║ąĖ ąŠą▒čāč湥ąĮąĖčÅ, ąĄčüą╗ąĖ ą║ąŠąĮąĄčćąĮąŠąĄ čüąŠčüč鹊čÅąĮąĖąĄ čéą░ą║ąŠąĄ ąČąĄ, ąĘąĮą░čćąĖčé ą╝ąĖąĮąĖą╝čāą╝ ąĮą░ą╣ą┤ąĄąĮ















![ąØą░ąĖčüą║ąŠčĆąĄą╣čłąĖą╣ čüą┐čāčüą║ čü ą╝ąŠą╝ąĄąĮč鹊ą╝ ’üĪ - ą║ąŠčŹčäčäąĖčåąĖąĄąĮčé ą╝ąŠą╝ąĄąĮčéą░ ą▓ ąĖąĮč鹥čĆą▓ą░ą╗ąĄ [0,1] ąØą░ ą┐ą╗ąŠčüą║ąĖčģ čāčćą░čüčéą║ą░čģ: ąŻčüą╗ąŠą▓ąĖąĄ čāč湥čéą░ ą╝ąŠą╝ąĄąĮčéą░ ą▓ ą┐čĆąĖčĆą░čēąĄąĮąĖąĖ ą▓ąĄčüąŠą▓ (ą┐čĆąĖą╝ąĄčĆ): ąöąŠčüč鹊ąĖąĮčüčéą▓ąŠ: čāčüą║ąŠčĆąĄąĮąĖąĄ čüčģąŠą┤ąĖą╝ąŠčüčéąĖ ąĮą░ ą┐ą╗ąŠčüą║ąĖčģ čāčćą░čüčéą║ą░čģ ąĖ ą▓ą▒ą╗ąĖąĘąĖ ą╗ąŠą║ą░ą╗čīąĮčŗčģ 菹║čüčéčĆąĄą╝čāą╝ąŠą▓.](https://image.slidesharecdn.com/lec4-111222191150-phpapp01/85/4-17-320.jpg)